
Физика в быту
Звуки с непрерывным спектром воспринимаются как шумы. Если полоса частот не слишком широка, мы можем грубо оценить высоту звука: рычание тигра – низкий звук (полоса низких частот), крик павлина – высокий. Если частоты более-менее равномерно распределены по всему звуковому диапазону, получается так называемый белый шум (пример: рёв близкого водопада).
Пение птиц ещё труднее передать звуками музыки, чем звучание колоколов, хотя шумом его тоже не назовёшь. С точки зрения спектра, это нечто промежуточное между звоном колокола и шумом. Каждая «нота» птичьего пения содержит не ряд кратных частот, как музыкальный звук, и не набор отдельных обертонов, как звук колокола, а несколько узких непрерывных полос частот, причем эти полосы во время песни «ползут» вверх или вниз по шкале частот, совершают резкие взлёты и падения. Именно эти взлёты и падения при переводе птичьего пения на язык музыки композиторы имитируют скачками на те или иные интервалы.
Частоты некоторых птичьих голосов простираются до 50 тысяч герц, уходя в область ультразвука, так что мы слышим лишь часть их песен.
Очень короткие звуки (стук в дверь, хлопок в ладоши) также воспринимаются как немузыкальные. Ведь нашему слуховому аппарату требуется некоторое время для определения периода колебаний и частоты основного тона, а при коротких звуках он просто не успевает это сделать. Спектры коротких звуков непрерывны, как и спектры шумов. Если ширина полосы частот невелика, мы можем приблизительно определить высоту тона, особенно в сравнении с другими подобными звуками. Вспомните, например, детский деревянный ксилофон, состоящий из дощечек разной длины. Удар по одной дощечке воспринимается просто как стук (немузыкальный звук), но ударяя по ряду дощечек-клавиш, мы уже слышим гамму.
Как создать музыкальный звук?
Одни предметы издают музыкальные звуки, а другие – немузыкальные. Самый простой, известный с древних времён источник музыкальных звуков – натянутая струна. Именно с изучения звучания струн началась математическая теория музыки, и основы её заложил в Древней Греции Пифагор (570–490 гг. до н. э.).
Самые простые движения, которые могут совершать точки струны, изображены схематически на рисунке 5: каждая точка движется туда-сюда, словно маятник, в результате струна изгибается так, что её форма соответствует части синусоиды. Длина полного периода такой синусоиды равна длине волны. Если оба конца струны закреплены, то на длине струны укладывается целое число полуволн (на верхнем рисунке – одна полуволна, на среднем – две, на нижнем – три). Такие колебания струны называются стоячими волнами или собственными колебаниями. Частоты этих колебаний кратны друг другу. Если одной полуволне соответствует частота f0, то частоты колебаний для более коротких волн равны 2f0 и 3f0. Как вы понимаете, возможны также колебания с частотами 4f0, 5f0 и так далее. Частота f0 является основной, а все остальные – обертонами или высшими гармониками.
Самое интересное: если вы просто ущипнёте струну, то многие обертоны возбудятся одновременно, и соответствующие им движения наложатся друг на друга, в результате форма струны в процессе колебаний будет уже не синусоидальной, а более сложной. Это как «спектральный анализ наоборот»: сложение простых гармоник даёт в результате сложное колебание.
Ущипнув струну, мы услышим музыкальный звук, высота тона которого соответствует основной частоте f0, а наличие обертонов придаст звуку тембральный окрас. Щипая струну в разных местах, мы меняем амплитуды обертонов и, значит, меняем тембр. Например, щипок ровно посередине струны исключает из движений чётные гармоники 2f0, 4f0 и т. д., так как для этих гармоник средняя точка струны должна быть неподвижна.
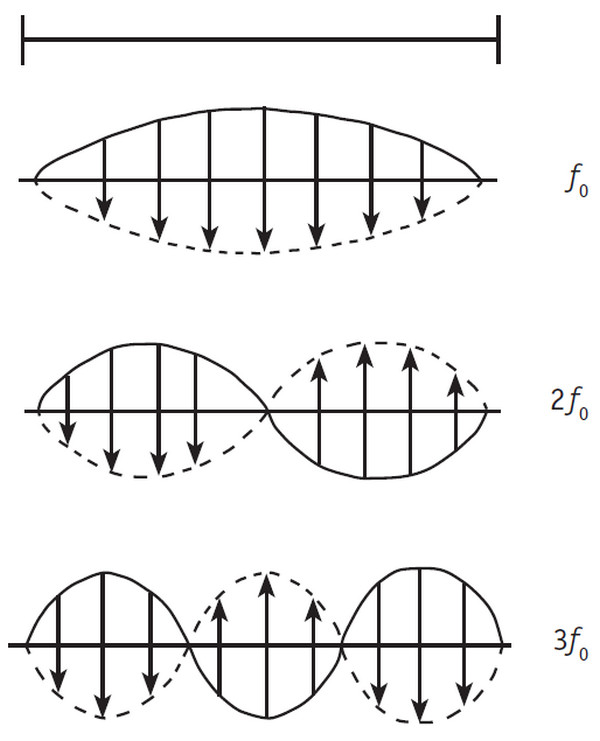
Рис. 5. Простейшие колебания струны (первая, вторая и третья гармоники)
Какими параметрами струны определяется её основная частота? Как видно из рисунка 5, чем длиннее струна, тем больше длина волны первой гармоники, а значит, частота колебаний меньше (низким звукам рояля соответствуют самые длинные струны, высоким – самые короткие). Основная частота f0 зависит также от натяжения струны: увеличивая натяжение, мы увеличиваем основную частоту (именно путём изменения натяжения струн настройщик добивается нужной частоты звука).
Как и для бегущих волн, длина стоячей волны λ связана с частотой колебаний частиц и скоростью v распространения волны универсальной формулой λ = v/f. Длина волны первой (основной) гармоники, как видно из рисунка 5, в два раза больше длины l струны: λ = 2l. Так что основная частота струны f0 = v/λ = v/2l. Увеличение натяжения струны приводит к увеличению скорости волн v, а значит, и к увеличению основной частоты.
Ещё одним простым телом, рождающим музыкальные звуки, являются цилиндрические трубы, ширина которых гораздо меньше длины (вспомним, например, трубы оргáна). Главным звучащим телом в трубах является наполняющий их воздух. Возбуждая на одном конце трубы движение воздуха с помощью вибратора, мы приводим в колебательное движение весь столб воздуха в трубе, и он рождает звуковую волну, бегущую от трубы к вашему уху. Основная частота f0 определяется длиной воздушного столба: чем длиннее труба, тем ниже её звук, как и для струны. И также наряду с основной частотой возбуждаются обертоны с кратными частотами.
Струны и воздушные трубы – основа всех музыкальных инструментов. Именно они рождают музыкальные звуки. Предметы же более сложных форм являются источниками немузыкальных звуков.
Можно ли увидеть звук?
Любой твёрдый предмет будет издавать те или иные звуки, если по нему ударять или, к примеру, водить по нему смычком. И у любого предмета конечных размеров, как и у струн, есть характерный набор собственных колебаний – возможных простейших движений его частиц. У большинства объемных тел частоты собственных колебаний образуют непрерывный спектр в пределах определённой полосы частот, зачастую весьма широкой, то есть воспринимаются ухом как шум. Например, ударив по столу, вы слышите звук, создаваемый возникающими колебаниями стола, но высоту тона определить не можете. Можно только предсказать, что шум от удара по массивному шкафу будет более низкочастотным, чем от удара по небольшому столику.
Немецкий физик и музыкант Эрнест Хладни сумел сделать видимыми собственные колебания плоских пластин разной формы (круглых, квадратных и прочих). Для этого он возбуждал в них колебания с помощью скрипичного смычка (рис. 6). При этом пластины издавали немузыкальные звуки разной степени «противности». На поверхность пластин он насыпал мелкий песок, который слетал с активно колеблющихся областей и концентрировался в тех местах, которые оставались практически неподвижными. Проводя смычком по краю пластины в разных местах, под разными углами и с различной скоростью, можно возбуждать различные собственные колебания и получать самые разные картины: иногда простые, иногда сложные, иногда красивые, иногда беспорядочные. Каждому типу колебаний соответствуют определённая «песочная картина» и своё неповторимое звучание.
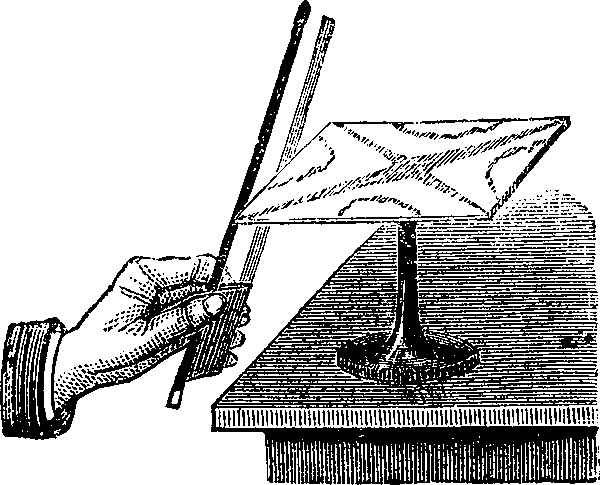
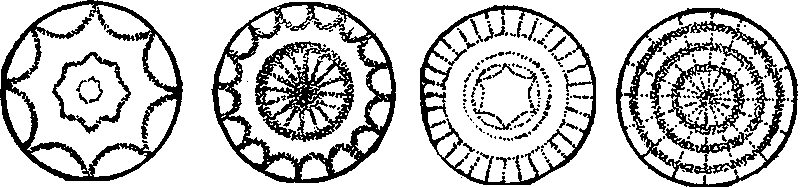
Рис. 6. Примеры фигур Хладни, полученных с помощью насыпанного на поверхность колеблющихся пластин песка
Резонанс и резонаторы
Но вернёмся к музыкальным звукам и струнам. Остаётся вопрос: почему тембры разных струнных инструментов (рояля, скрипки, виолончели и прочих) столь отличаются друг от друга, хотя струны везде практически одинаковые? Всё дело в резонаторах. Давайте разберёмся, что это такое.
До сих пор мы говорили о собственных колебаниях тел – таких колебаниях, которые они совершают «по своему сценарию», стоит только вывести их из равновесия, сообщив запас энергии (ущипнуть струну, постучать по столу, ударить по металлической пластинке, провести смычком и т. д.). Как мы уже знаем, собственные колебания происходят с собственными частотами – с любой из них или одновременно со многими. А что будет, если мы будем извне «навязывать» упругому телу колебания с какой-то частотой? Возникнут колебания, которые называют вынужденными.
Попробуйте закрепить один конец длинного шнура (желательно эластичного), а другой конец периодически раскачивать рукой. По шнуру побежит какая-то рябь. Но постарайтесь подобрать такую частоту качаний, чтобы на длине шнура уложилась одна или несколько полуволн (как на рисунке 5) – шнур отзовётся колебанием значительной амплитуды. Мы наблюдаем при этом явление резонанса – резкое возрастание амплитуды вынужденных колебаний при совпадении частоты вынуждающего периодического воздействия с любой из собственных частот.
Говорят, что Карузо мог разбить бокал голосом, взяв ноту надлежащей высоты. В середине XIX века во Франции рухнул мост, по которому проходил отряд солдат. В Петербурге в XIX веке таким же образом обрушился Египетский мост (с тех пор солдатам запрещено ходить по мостам в ногу). Это всё примеры проявления резонанса.
Слово «резонанс» происходит от французского resonance – звучать, откликаться.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Всего 10 форматов

