
Рациональность. Что это, почему нам ее не хватает и чем она важна
Ученые, изучающие механизмы мышления и принятия решений, раз за разом убеждаются, что люди становятся рациональнее, когда имеют дело с наглядными и имеющими прямое отношение к делу данными, – и посему позвольте мне перейти к конкретным примерам. Каждый из этих классических примеров – из области математики, логики, теории вероятности и прогнозирования – проливает свет на особенности нашего мышления и отлично подходит в качестве первого знакомства с нормативными стандартами рациональности (и типичными для нас отклонениями от них), о которых я буду рассказывать дальше.
Три простые математические задачи
Мы все помним, как учителя в школе пытали нас алгебраическими задачами, спрашивая, где поезд, который вышел из пункта А со скоростью 70 км/ч, встретится с поездом, который со скоростью 60 км/ч вышел ему навстречу из пункта В, расположенного в 260 км от пункта А. Эти три попроще, их можно решить в уме:
● Телефон и чехол к нему вместе стоят 110 долларов. Телефон дороже чехла на 100 долларов. Сколько стоит чехол?
● 8 принтеров печатают восемь брошюр за 8 минут. За сколько минут 24 принтера напечатают 24 брошюры?
● Часть поля заросла сорняками. Каждый день эта часть увеличивается в два раза. За 30 дней сорняки покроют все поле. За сколько дней они покроют половину поля?
Ответ на первый вопрос – 5 долларов. Если вы не отличаетесь от большинства людей, вы сказали, что 10 долларов. Но в таком случае телефон стоил бы 110 долларов (на 100 больше, чем чехол), а телефон вместе с чехлом – 120 долларов.
Ответ на второй вопрос – 8 минут. Принтер печатает брошюру 8 минут, так что, пока число принтеров равно числу брошюр и все принтеры работают одновременно, времени им потребуется ровно столько же.
Ответ на третий вопрос – 29 дней. Если площадь заросшей сорняками части поля каждый день удваивается, тогда, представив себе полностью покрытое сорняками поле и рассуждая от конца к началу, мы поймем, что половина поля была покрыта сорняками за день до этого.
Экономист Шейн Фредерик предлагал эти три задачи (в разных вариантах) тысячам студентов высших учебных заведений. Пять из шести давали как минимум один неверный ответ; каждый третий не угадал ни разу[19]. Но задачки простые – узнав правильные ответы, практически все понимают, где ошиблись. Дело в том, что людей сбивают с толку внешние признаки формулировки, неважные для решения, но ошибочно кажущиеся им важными, например круглые числа 100 и 10 в первой задаче и тот факт, что число принтеров равно числу затраченных минут во второй.
Фредерик назвал свой незамысловатый опросник тестом когнитивной рефлексии (Cognitive Reflection Test) и предположил, что тот выявляет расхождение между двумя системами мышления, которые позднее обрели широкую известность благодаря бестселлеру Канемана (он периодически выступал соавтором Фредерика) «Думай медленно, решай быстро» (Thinking, Fast and Slow, 2011). Система 1 срабатывает моментально и непроизвольно – она-то и искушает нас неверными ответами. Система 2 требует сосредоточенности, мотивации и применения усвоенных правил – она помогает отыскать верное решение. Никто, конечно, не думает, что у нас в мозгу реально сосуществуют две отдельные анатомические структуры; здесь имеются в виду два способа обработки информации, каждый из которых требует работы множества мозговых структур. Система 1 означает дать мгновенный ответ; система 2 означает подумать дважды.
Тест когнитивной рефлексии демонстрирует, что ошибаемся мы скорее по невнимательности, чем по глупости[20]. Даже студенты гордящегося своими математическими традициями Массачусетского технологического института в среднем давали два правильных ответа из трех. Показанный результат, разумеется, коррелирует с математическими навыками, но, кроме того, зависит и от терпеливости. Люди, описывающие себя как неимпульсивных и готовые подождать месяц и получить бóльшую сумму денег, отказавшись от меньшей прямо сейчас, реже попадались в эти ловушки[21].
Два первых вопроса кажутся задачами с подвохом. Это потому, что они снабжают нас деталями, которые, всплыви они в обычном разговоре, имели бы отношение к делу, но в этих примерах только уводят в сторону. (Люди лучше справляются с первым заданием, если телефон, например, на 73 доллара дороже чехла, а телефон и чехол вместе стоят 89 долларов.)[22] Но, что ни говори, в реальной жизни тоже полно ведущих в никуда тропинок и песен сирен, которые манят прочь от верного решения, и сопротивляться им – непременное условие рациональности. Люди, которые не в силах устоять перед соблазном дать быстрый, но неверный ответ в тесте когнитивной рефлексии, оказываются менее рациональными и в других отношениях, например чаще отказываются от выгодного предложения, требующего некоторого ожидания или определенного риска.
Третья задача – та, что про сорняки, – не вопрос с подвохом; она обнажает объективно существующую когнитивную недостаточность. Человеческая интуиция не в состоянии постичь экспоненциальный рост (геометрическую прогрессию): как нечто может увеличиваться с возрастающей скоростью, пропорциональной тому, насколько оно уже велико, например сложный процент, экономический рост или распространение инфекционного заболевания[23]. Люди путают экспоненциальный рост с равномерным нарастанием или с ростом с небольшим ускорением, а их воображение не поспевает за беспрестанным удваиванием. Если вы будете каждый месяц класть по 400 долларов на пенсионный счет под 10 % годовых, какую сумму составят ваши сбережения спустя 40 лет? Многие полагают, что это будет что-то около 200 000 долларов – эту цифру можно получить, если умножить 400 на 12 на 110 % и на 40 лет. Кое-кто, понимая, что такой ответ не может быть верным, корректирует свое предположение в большую сторону, но почти всегда недостаточно. Практически никто не дает правильного ответа: 2,5 миллиона долларов. Как выясняется, люди, слабо понимающие, что такое экспоненциальный рост, меньше откладывают на старость и накапливают больше долгов по кредитным картам – обе эти дороги ведут к нищете[24].
Неспособность представить, насколько резким может быть экспоненциальный рост, вводит в заблуждение даже экспертов, в том числе экспертов по когнитивным искажениям. Когда в феврале 2020 г. ковид-19 пришел в США и Европу, некоторые специалисты по общественным наукам (включая двух героев этой книги, хотя и не самого Канемана) высказывали мнение, будто население охвачено иррациональной паникой: люди читают об одном-двух прискорбных случаях и впадают в заблуждение под названием «эвристика доступности» или «пренебрежение вероятностью». Они отмечали, что связанный с ковидом реальный риск был на тот момент ниже рисков умереть от гриппа или ангины – рисков, которые все безропотно принимают[25]. Специалисты по ошибкам допустили тут ошибку, недооценив ускоряющийся темп, с каким способно распространяться заболевание столь заразное, как ковид: каждый новый пациент не только заражает других людей, но и превращает их всех в распространителей болезни. Первый американец скончался от ковида 1 марта, а затем смертность быстро нарастала, достигнув в последующие недели 2, 6, 40, 264, 901 и 1729 смертей в день, что к 1 июня в сумме составило более 100 000 и превратило ковид в важнейшую причину смерти в стране[26]. Конечно, авторам тех мало кем прочитанных редакционных колонок нельзя ставить в вину беззаботность, из-за которой столь многие представители власти и простые граждане проявили опасную халатность, но их заявления демонстрируют, насколько глубокими и устойчивыми могут быть когнитивные искажения.
Почему же люди перенедооценивают (как мог бы выразиться Джордж Буш – младший) экспоненциальный рост? Следуя славной традиции доктора из пьесы Мольера, который говорил, что опиум усыпляет людей благодаря своему снотворному эффекту, специалисты видят корни этого в «ошибке экспоненциального роста». Чтобы вырваться из пут рекурсии, можно отметить отсутствие в природе экспоненциальных процессов (если не считать исторических новшеств вроде экономического роста и сложного процента). То, что не может длиться вечно, рано или поздно кончается: организмы размножаются только до того момента, когда они истощают, загрязняют или насыщают свою среду обитания, после чего экспоненциальная кривая загибается вниз и выходит на плато. Это касается и пандемий, которые гаснут, когда достаточная доля восприимчивых к возбудителю особей погибает или вырабатывает иммунитет.
Простая логическая задача
Если что-то лежит в основе рациональности, то это наверняка логика. Прообраз рационального умозаключения – силлогизм «Если Р, то Q. P. Следовательно, Q». Рассмотрим простой пример.
Предположим, на аверсе монет некой страны помещают портрет одного из ее выдающихся государей, а на реверсе – изображение какого-нибудь представителя ее великолепной фауны. Теперь рассмотрим простое правило «если – то»: «Если на одной стороне монеты изображен король, то на другой будет птица». Перед вами четыре монеты с изображением короля, королевы, лося и утки. Какие из них нужно перевернуть, чтобы определить, не было ли нарушено правило?

Если вы не отличаетесь от большинства, вы скажете: «Короля» или «Короля и утку». Правильный ответ: «Короля и лося». Почему? Никто не спорит, что короля перевернуть нужно: если на обороте вы не найдете птицы, это сразу же укажет на нарушение правила. Большинство понимает, что переворачивать королеву смысла нет, потому что правило гласит: «Если король, то птица», а о монетах с королевой ничего не сказано. Многие считают, что нужно перевернуть утку, но, если подумать, очевидно, что эта монета нам ничем не поможет. Правило гласит: «Если король, то птица», а не «Если птица, то король» – если на обратной стороне монеты с уткой отчеканена королева, правило не нарушается. А теперь давайте подумаем про лося. Если вы перевернете монету с лосем и найдете на обратной стороне короля, правило «Если король, то птица» будет нарушено. Следовательно, верный ответ: «Король и лось». В среднем его дают только 10 % опрошенных.
Задачу выбора Уэйсона (названную в честь придумавшего ее когнитивного психолога Питера Уэйсона) уже 65 лет предлагают испытуемым с самыми разными условиями типа «если Р, то Q». (В оригинальной версии использовались карточки с буквой с одной стороны и цифрой с другой, а правило звучало примерно так: «Если с одной стороны D, то с другой стороны 3».) Снова и снова люди переворачивают Р или Р и Q и не догадываются перевернуть не-Q[27]. И дело не в том, что они не способны понять правильный ответ. Как и с задачами из теста когнитивной рефлексии, когда им объясняют, в чем загвоздка, они хлопают себя по лбу и соглашаются[28]. Но их нерефлексивная интуиция, будучи предоставлена самой себе, не в состоянии уловить эту логику.
Что это говорит нам о человеческой рациональности? Часто утверждается, что такие факты проливают свет на нашу предвзятость подтверждения – дурную привычку искать подтверждения своим убеждениям и не интересоваться сведениями, способными их пошатнуть[29]. Люди считают сновидения вещими, потому что помнят, как им приснилось, что с родственницей приключилось несчастье, и оно-таки приключилось, но забывают обо всех тех случаях, когда с родственницей все было в порядке, хотя им и приснилось, что у нее неприятности. Они убеждены, что иммигранты виновны в основной массе преступлений, потому что прочли в новостях, как иммигрант ограбил магазин, но не вспоминают обо всех магазинах, ограбленных уроженцами своей собственной страны.
Предвзятость подтверждения – не только распространенное объяснение человеческой глупости, но и точка приложения сил для укрепления рациональности. Фрэнсис Бэкон (1561–1626), которому ставят в заслугу разработку научного метода познания, писал о человеке, которого привели в церковь и показали ему портреты моряков, выживших в кораблекрушениях благодаря принесенным священным обетам. «А где изображения тех, кто погиб после того, как принес обет?» – спросил тот[30][31]. Бэкон замечает:
Таково основание почти всех суеверий – в астрологии, в сновидениях, в поверьях, в предсказаниях и тому подобном. Люди, услаждающие себя подобного рода суетой, отмечают то событие, которое исполнилось, и без внимания проходят мимо того, которое обмануло, хотя последнее бывает гораздо чаще[32].
Вторя известному аргументу философа Карла Поппера, большинство современных ученых настаивают, что водораздел между псевдонаукой и наукой пролегает по линии, за которой сторонники гипотезы намеренно ищут свидетельства, способные ее опровергнуть, и принимают эту гипотезу, только если она устояла в ходе такой проверки[33].
Как же люди справляются с повседневной жизнью, если не способны применять самые элементарные логические правила? Отчасти ответ заключается в том, что задача выбора Уэйсона – очень своеобразное упражнение[34]. Оно не требует применить силлогизм, чтобы прийти к нужному заключению («Вот монета с королем. Что на обратной стороне?») или проверить правило в целом («Верно ли сказанное применительно к дизайну монет этой страны?»). Там спрашивается, работает ли правило для каждой монеты из того конкретного набора, что лежит сейчас на столе. К тому же – и это вторая половина ответа – люди прекрасно применяют законы логики, когда правило касается дозволений и запретов, с которыми они сталкиваются в повседневной жизни, а не случайного чередования символов и знаков.
Предположим, чтобы отправить письмо третьим классом, на него нужно наклеить марку ценой в 50 центов, но, чтобы воспользоваться экспресс-почтой, требуется марка за 10 долларов. Следовательно, верно оформленное отправление должно удовлетворять правилу: «Если письмо помечено для отправки экспресс-почтой, на нем должна быть наклеена марка за 10 долларов». Предположим, отметка о классе помещается на лицевой стороне конверта, а марка – на обратной, поэтому почтовому работнику, чтобы проверить, не нарушил ли отправитель правило, нужно перевернуть конверт. Перед вами четыре конверта. Какие два нужно перевернуть?

Верным ответом снова будет Р и не-Q, а именно конверт с надписью «Экспресс» и тот, на котором наклеена марка за 50 центов. Хотя задача эквивалентна задаче с четырьмя монетами, на этот раз с ней без труда справляются практически все. Оказывается, нам важно само содержание логической задачи[35]. Когда правило «если – то» описывает договоренность, касающуюся прав и обязанностей («Если хочешь воспользоваться преимуществом, заплати»), нарушение правила (воспользоваться преимуществом, не уплатив полную стоимость) равно мошенничеству, а люди интуитивно понимают, что нужно сделать, чтобы поймать плута. Они не проверяют тех, кто не претендует на преимущество, или тех, кто его оплатил, а сосредоточиваются на тех, кто, возможно, пытается обстряпать дельце.
Когнитивные психологи спорят, какой именно контекст внезапно превращает людей в логиков. Тут сгодится не любой конкретный сценарий – он должен описывать именно те виды логических задач, к которым мы привыкли в ходе взросления, а возможно, даже в ходе эволюции. Одна из тем, способных разблокировать логику, – контроль за осуществлением прав и выполнением обязанностей, другая – слежение за угрозами. Люди знают, что, для того чтобы проконтролировать соблюдение правила: «Если едешь на велосипеде, нужно надеть шлем», им нужно удостовериться, что на ребенке на велосипеде надет шлем и что ребенок без шлема на велосипед не садится.
Честно говоря, разум, который замечает нарушение условного правила, только если оно сигнализирует о мошенничестве или опасности, не назовешь истинно логичным. По определению для логики важна форма утверждения, а не его содержание: каким образом Р и Q соединяются операторами если, то, или, и, не, некоторые и все безотносительно того, что означают эти самые Р и Q. Логика – вершинное достижение человеческого ума. Она упорядочивает наш мыслительный процесс, помогая ему справляться с незнакомым или абстрактным содержанием, таким как законы государственного управления или науки. Воплощенная в кремнии, она превращает мертвую материю в мыслящую машину. Но неискушенный человеческий разум оперирует не универсальным, независящим от содержания инструментом с формулами вроде «[Если Р, то Q] эквивалентно не [Р и не Q]», в которые можно подставить любые Р и Q. Он вооружен набором инструментов более узкого назначения, сваливающими в одну кучу содержание проблемы и правила логики (без этих правил инструменты не будут работать). Людям непросто вычленить формулы и применить их к новым, абстрактным или на первый взгляд бессмысленным задачам. Для этого-то нам и нужны укрепляющие рациональность институты вроде системы образования. Они дополняют экологическую рациональность, с которой мы рождены и воспитаны, – наш животный здравый смысл и природное чутье – мощными инструментами мышления более широкого применения, которые лучшие умы человечества оттачивали тысячелетиями[36].
Простая задача на вероятность
Одной из известнейших телевизионных игр эпохи расцвета этого жанра была игра «Давайте заключим сделку» (Let's Make a Deal), выходившая в телеэфир с 1950-х по 1980-е гг. Ведущий, Монти Холл, стал широко известен в весьма узких кругах, когда в его честь назвали парадокс из области теории вероятности, в общих чертах основанный на сценарии шоу[37]. Участника ставят перед тремя дверьми. За одной из них новехонький сверкающий автомобиль. За двумя другими – по козе. Участник выбирает дверь, скажем дверь № 1. Нагнетая напряжение, Монти открывает одну из двух оставшихся дверей, скажем дверь № 3, и показывает зрителям козу. Дополнительно накаляя обстановку, он дает участнику возможность либо не менять решения, либо изменить его, выбрав другую дверь. Вы – участник. Что бы вы сделали?
Чуть ли не каждый остается при своем выборе[38]. Игроки думают, что, раз машина может оказаться за любой из трех дверей, а дверь № 3 из игры выбыла, шансы, что машина стоит за дверью № 1 или за дверью № 2, равны и составляют 50/50. Хотя никакого вреда переключение не принесет, они считают, что и пользы от него не будет. Поэтому они придерживаются первоначального выбора – либо по инерции, либо из гордости, либо из-за смутного ощущения, что проигрыш при изменении решения принесет им больше огорчения, чем победа – радости.
О парадоксе Монти Холла заговорили в 1990 г., когда о нем написали в колонке «Спроси у Мэрилин» в журнале Parade, который вкладывался в воскресные издания сотен американских газет[39]. Вела колонку Мэрилин вос Савант, в то время известная как «самая умная в мире женщина»: она была внесена в Книгу рекордов Гиннесса как обладательница самого высокого в мире IQ. Вос Савант писала, что участнику лучше бы передумать: шансы, что машина находится за дверью № 2, составляют два из трех, шансы, что она стоит за дверью № 1, – только один из трех. В ответ в журнал пришло около десяти тысяч писем (примерно тысяча из них – от обладателей ученых степеней, в основном от математиков и статистиков), в которых утверждалось, что она не права. Вот несколько примеров:
Вы прокололись, и прокололись по-крупному! Похоже, вы не понимаете действующих здесь базовых принципов, так что я вам объясню. После того как ведущий показывает козу, ваши шансы угадать правильно составляют один к двум. Поменяете вы свой выбор или нет, шансы не изменятся. Математической безграмотности в стране и так достаточно, и нам не нужно, чтобы ее распространяла еще и обладательница самого высокого в мире IQ. Стыдитесь!
СКОТТ СМИТ, КАНДИДАТ НАУК, ФЛОРИДСКИЙ УНИВЕРСИТЕТЯ уверен, что вы получите массу писем на эту тему от старшеклассников и студентов колледжей. Может, вам стоит сохранить себе пару адресов, чтобы при случае попросить помощи в работе над будущими колонками.
У. РОБЕРТ СМИТ, КАНДИДАТ НАУК, УНИВЕРСИТЕТ ШТАТА ДЖОРДЖИЯМожет, женщины иначе понимают математические задачи – не так, как мужчины.
ДОН ЭДВАРДС, САНРИВЕР, ОРЕГОН[40]В числе несогласных был даже Пал Эрдёш (1913–1996), прославленный математик, настолько плодовитый, что ученые меряются своими «числами Эрдёша» – длиной кратчайшей цепи соавторов по публикациям, связывающей их с этим великим теоретиком[41].
Но математики-мужчины, свысока объяснявшие свое решение самой умной в мире женщине, ошибались, а вот она была права. Участнику лучше бы изменить свое решение. И нетрудно понять почему. Автомобиль может стоять за любой из трех дверей. Давайте подумаем о каждой из них и подсчитаем, сколько раз из трех вы выиграете, придерживаясь одной из двух возможных стратегий. Вы выбрали дверь № 1 – конечно, это просто мы ее так назвали; пока Монти придерживается правила: «Открой невыбранную дверь, за которой стоит коза; если коза за обеими, открой любую», шансы выиграть равны, какую бы дверь вы ни выбрали.
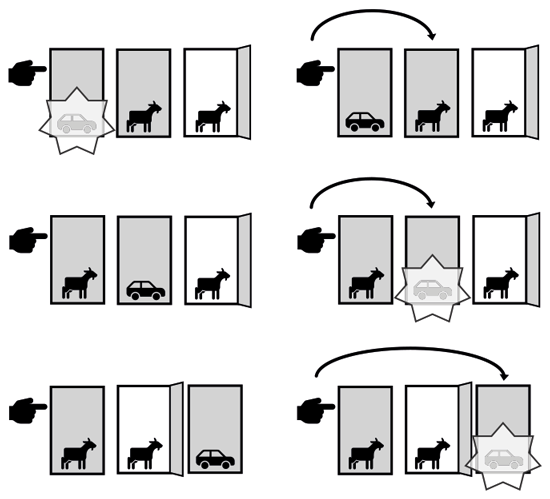
Скажем, ваша стратегия – «не менять выбора» (левая колонка на рисунке). Если машина стоит за дверью № 1 (слева вверху), вы выиграете. (Неважно, какую из двух оставшихся дверей откроет Монти, потому что вы все равно не переключитесь ни на одну из них.) Если машина за дверью № 2 (слева посередине), вы проиграете. Если машина за дверью № 3 (слева внизу), вы опять проиграете. Так что шанс выиграть, придерживаясь стратегии «не менять выбора», составляет один к трем.
Давайте теперь рассмотрим стратегию «изменить выбор» (правая колонка). Если машина за дверью № 1, вы проиграете. Если машина за дверью № 2, Монти открыл бы дверь № 3, так что вы переключитесь на дверь № 2 и выиграете. Если же машина за дверью № 3, он открыл бы дверь № 2, и, переключившись на дверь № 3, вы снова выиграете. Шанс выиграть при стратегии «изменить выбор» составляет два к трем, что в два раза больше, чем при стратегии «не менять выбора».
Прямо скажем, не бином Ньютона[42]. Не хотите просчитывать вероятности – можете сами сыграть пару раундов, вырезав из картона дверцы и пряча за ними игрушки, а потом суммировать результаты, как сделал однажды Холл, чтобы убедить скептически настроенного журналиста. (А еще в эту игру можно сыграть онлайн.)[43] Или же вы можете призвать на помощь интуицию и рассудить так: «Монти знает ответ и дает мне подсказку; будет глупо ею не воспользоваться». Почему же математики, университетские профессора и другие важные персоны так опростоволосились?
Конечно, некоторым критическое мышление отказывало из-за сексизма, личных предрассудков и профессиональной ревности. Вос Савант – привлекательная, элегантная женщина, не отмеченная академическими регалиями, автор колонки в бульварном журнале, где публикуются сплетни и кулинарные рецепты; ее вовсю высмеивают в вечерних ток-шоу[44]. Она не соответствует стереотипу математика; к тому же, прославившись благодаря Книге рекордов Гиннесса, вос Савант сделалась соблазнительной мишенью для нападок.
Но часть проблемы – сама проблема. Как и в вопросах с подвохом в тесте когнитивной рефлексии и в задаче выбора Уэйсона, в парадоксе Монти Холла есть что-то, выставляющее напоказ бестолковость нашей системы 1. Но и система 2 здесь тоже не блещет. Многие не в силах усвоить ответ даже после объяснения; в их числе сам Эрдёш, который, поправ идеалы математической науки, позволил себя убедить только после многократной симуляции игры[45]. Многие упирались, даже воочию пронаблюдав за симуляцией, и даже после того, как неоднократно сыграли на деньги. В чем же причина такого резкого расхождения между нашей интуицией и законами случайности?
Разгадка кроется в самонадеянных объяснениях, которыми всезнайки оправдывали свою ошибку, – зачастую это просто решения, бездумно перенесенные с других задач по теории вероятности. Одни настаивают, что каждой из неизвестных альтернатив (в данном случае закрытых дверей) нужно приписать равную вероятность. Это верно, если речь идет о симметричном инвентаре для азартных игр вроде монет или игральных костей, и это разумная отправная точка для рассуждений, если вам абсолютно ничего не известно об альтернативах. Но это отнюдь не закон природы.
Другие представляют себе цепочку причин и следствий. Козы и автомобиль заняли свои места до того, как ведущий открыл дверь, и то, что он ее открыл, не меняет их местоположения. Указание на отсутствие причинно-следственных связей – хороший способ развенчать другие заблуждения, такие как «ошибка игрока», поддавшись которой игроки в рулетку почему-то думают, что после того, как несколько раз подряд выпало «красное», в следующем раунде должно выпасть «черное», хотя на самом деле рулетка ничего не помнит и результат одного ее вращения никак не зависит от другого. Один из корреспондентов вос Савант снисходительно объяснял:

