Геометрия скорби. Размышления о математике, об утрате близких и о жизни

1. Геометрия

Жаль, что уже не увижу деревья, какими видел их раньше.

Представьте, что сейчас ранняя весна, вечерние сумерки, и вы сидите в каком-то малознакомом парке. Что вы увидите, подняв глаза от страницы этой книги? Вероятно, замысловатый узор из светлых и темных силуэтов, вливающихся в шероховатые столбы – стволы деревьев; толстые ветви, ветки потоньше, мелкие прутья; потрепанные обрывки плоскостей – листьев. А еще цветы и траву. Геометрические формы позволяют нам узнавать или, по крайней мере, называть то, что нас окружает.

Мы видим, как зрительно меняются формы, распознаём их движение – наблюдаем, например, как листья и ветки покачиваются от легкого ветерка.

Листья на вершине высокого дерева всё еще освещены солнцем, хотя ствол погружен в темноту. Мы обычно говорим, что тьма спускается, но здесь она как будто поднимается (а если мы придем в парк утром, то увидим, как по стволу дерева спускается рассвет). Геометрия солнца и земли являет во всей простоте то, чего мы раньше не замечали в этом мире.

На протяжении веков художники великолепно чувствовали геометрию. Приведу лишь несколько примеров. А если вы немного покопаетесь в «Гугле», то найдете еще больше.

Построенный в IX, а затем воссозданный в XIII веке дворец Альгамбра в испанской Гранаде – прекрасный образец исламского искусства и архитектуры. Множество декоративных мозаик, включая ту, что приведена ниже, являются замощениями плоскости правильными многоугольниками.

Это фигуры, которыми можно покрыть всю поверхность без наложений и пропусков, поскольку все они соприкасаются друг с другом лишь краями (частично или полностью). Клетки шахматной доски или шестиугольные пчелиные соты – наиболее известные из таких фигур, но есть и другие.

В книге Бранко Грюнбаума[17] и Джоффри Шепарда[18]«Плитки и паттерны» (этот семисотстраничный труд вполне заслуживает эпитета «всеобъемлющий») приводится огромное количество примеров не столько из области искусства, сколько из области математики[19]. Вообще существует семнадцать различных паттернов, обладающих красноречивым названием «группы орнамента». То, что таких паттернов всего семнадцать, было доказано в конце XIX века, но исламские художники знали об этих способах мощения за сотни лет до того, как русский кристаллограф и математик Евграф Фёдоров представил свое доказательство данного тезиса[20]. Иногда художники интуитивно делают открытия, которые математики проверяют и доказывают лишь многие годы спустя.

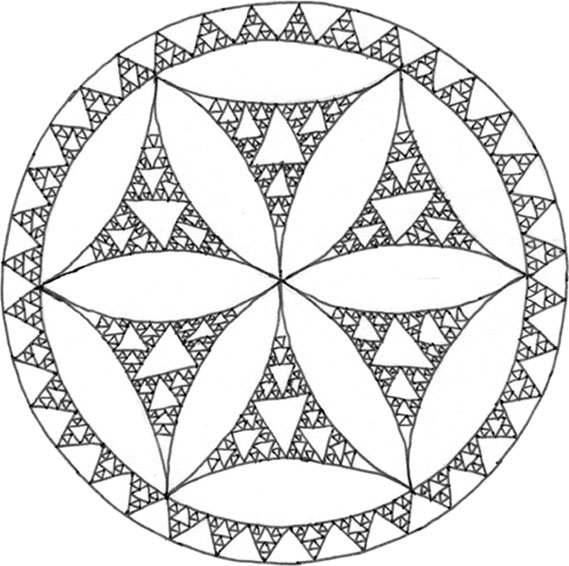
Взаимодействие геометрии и искусства отражают также подобные треугольники. Из школьных уроков геометрии мы знаем, что два треугольника подобны, если они имеют одинаковую форму, даже если у них разные размеры. Фигура называется самоподобной, если она состоит из элементов, каждый из которых подобен целой фигуре. На верхнем рисунке слева приведена фигура, состоящая из треугольников, расположенных внутри других треугольников, – это треугольник Серпинского, одна из самых известных самоподобных фигур. Чтобы увидеть ее самоподобие, обратите внимание на то, что она состоит из трех частей – нижней левой, нижней правой и центральной верхней, – каждая из которых подобна целому треугольнику. Об этом треугольнике мы поговорим подробнее в третьей главе.

Фракталы (класс фигур, впервые описанных математиком Бенуа Мандельбротом) – фигуры, построенные из частей, среди которых каждая так или иначе подобна целому. Кусочек береговой линии, если его рассматривать вблизи, выглядит так же, как ее большой отрезок с большого расстояния; листочек папоротника выглядит как сам папоротник в миниатюре; двухметровая нить ДНК сворачивается внутри клеточного ядра диаметром примерно в одну миллионную часть ее длины, повторяя один и тот же способ сложения каждый раз в меньшем масштабе. Это фракталы, которые мы наблюдаем в природе. Простейшие фракталы – самоподобные фигуры вроде треугольника Серпинского.

Круглый узор под треугольником на рисунке слева – это плиточный орнамент XIII века в одном из итальянских соборов, представляющий собой шесть фигур, напоминающих изогнутые треугольники Серпинского, окруженные кольцом треугольников поменьше[21]. (Делая данный набросок, я измерил и зарисовал основные элементы, а остальное заполнил на глаз. Это заняло немало времени. Но оригинал вырезался вручную, элемент за элементом, а потом они складывались вместе. Когда я об этом думаю, тот час, что я провел над рисунком, уже не кажется таким долгим.)

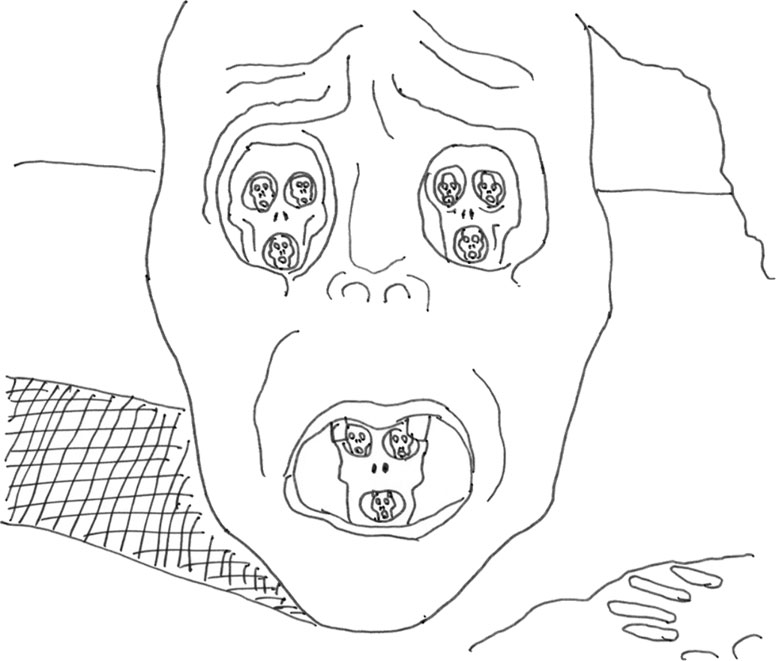
Художники размышляли над самоподобием многие века. Почему? Потому что оно часто встречается в природе, а художники внимательно присматриваются к ней.

Более свежим примером использования самоподобия является картина Дали «Лицо войны» (1940), изображающая бесчисленные ужасы гражданской войны в Испании. На картине мы видим лицо, в глазницах которого и во рту заключены другие лица, в чьих глазницах и ртах снова заключены лица, и так далее еще на несколько уровней вглубь. Паттерн очень напоминает треугольник Серпинского – повторение фигур, выстроенных в треугольник, только в данном случае располагающихся наверху слева и справа и внизу посредине. Картина Дали гораздо страшнее, чем мой набросок: по обеим сторонам головы без тела вьются клубки змей[22]

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

1

1. «Хуже», ведь, во что бы вы ни верили, отрицание утраты порочит память о жизни покойного. Даже маленькие дети достойны того, чтобы с ними говорили честно, пусть эта честность будет немного отфильтрованной и смягченной, но всё же останется честностью. Скажите детям: печалиться – нормально; никогда не говорите им, что не бывает причин для грусти.

2

1* Здесь и далее цифрами обозначены примечания автора, астерисками – примечания редактора.

3

2* Этан Канин (род. 1960) – американский писатель, педагог и врач.

4

2. Моя дорогая приятельница Кристин Уолдрон подарила мне книгу Этана Канина «Альманах для сомневающихся» (Canin E. A Doubter’s Almanac. New York: Random House, 2016). Многие годы я читал работы Канина и восхищался ими. Кристин подвела меня к этой книге раньше, чем я сам бы до нее добрался – на самом деле, это случилось вскоре после смерти отца, которая, очевидно, повлияла на мое восприятие слов Канина.

5

3* Дословно: «Если бы не неудача, то и удачи

6

3. Книги Джона Арчера (Archer J. The Nature of Grief. New York: Taylor & Francis, 1999) и Барбары Кинг (King B. How Animals Grieve. Chicago: University of Chicago Press, 2014) являются прекрасной отправной точкой для глубоких размышлений на тему скорби. Книга Кинг более повествовательная, более личная; книга Арчера трактует тему более абстрактно. В этом смысле обе работы дополняют друг друга, обе познавательны. Во второй главе «Природы скорби» дан исторический обзор исследований по теме скорби. В своей статье «Эволюционные основы для понимания скорби» (Nesse R. An Evolutionary Framework for Understanding Grief / ed. D. Carr, R. Nesse, C. Wortman // Spousal Bereavement in Late Life. New York: Springer, 2005. P. 195–226) Рэндольф Несси дает нам четкое объяснение эволюционного происхождения скорби в контексте своей новаторской работы по эволюционной медицине, написанной совместно с Джорджем Уильямсом (см.: Nesse R., Williams G. Why We Get Sick: The New Science of Darwinian Medicine. New York: Random House, 1994).

7

4* Александр Шенд (1858–1936) – английский писатель, адвокат, один из основателей Британского психологического общества.

8

4. Книга Александра Шенда «Основы характера» (Shand A. The Foundations of Character. London: Macmillan, 1914) является первым систематическим исследованием скорби.

9

5. В третьей главе «Природы скорби» Арчер исследует скорбь сквозь призму искусства.

10

6. Эти книги Жан-Поля Сартра дали мне первое и самое ясное на сегодняшний день представление о литературе как о наиболее прямом пути к глубоким истинам. Сартр тщательно анализирует эту тему с точки зрения философии в книге «Бытие и ничто: опыт феноменологической онтологии». Правда, подзаголовок книги не слишком вдохновляет. В цикле романов «Дороги свободы» («Возраст зрелости», «Отсрочка» и «Смерть в душе») рассказы персонажей приводят к схожему пониманию. Их истории вызывают отклик.

11

7. Музыка придает звучание, чувство, кристально выверенное придыханием в голосе и подчеркнутое ритмом. Потом к ней иногда добавляется задумчивый фортепианный монолог, ансамблевые инструменты или сложная сеть людских голосов, наслаивающихся друг на друга. Порой звук взмывает ввысь, то дополняя, то заглушая поэзию текста. Благодаря музыке мы можем прочувствовать всю многокрасочность жизни более непосредственно и более многослойно, чем представляет нам текст. Вот несколько примеров: Натали Мерчант, «My Skin» с альбома «Ophelia» (Elektra, 1998) и «Beloved Wife» с альбома «Tiger Lily» (Elektra, 1995); Лорина Маккеннитт, «Dante’s Prayer» с альбома «The Book of Secrets» (Quinlan Road, 1997); Филип Гласс, «Сочленение № 5» из оперы «Эйнштейн на пляже» (Elektra, 1993). Я мог бы назвать еще десятки, если не сотни композиций. Как и вы. Интересно, чей список был бы длиннее?

12

5* Йо Йо Ма (род. 1955) – известный американский виолончелист китайского происхождения, композитор.

13

8. Великолепный фильм Энга Ли «Крадущийся тигр, затаившийся дракон» («Коламбия Пикчерз», 2000) завершается захватывающим (в буквальном смысле слова – во всяком случае, у меня перехватило дыхание, и, судя по приглушенным всхлипываниям, я был не один такой в зале) «Прощанием» в исполнении Йо Йо Ма.

14

9. Песня Сии «Breathe Me» из альбома «Color the Small One» (Astralwerks, 2006).

15

10. Родители не должны переживать своих детей. Задолго до смерти родителей младший брат моей мамы, Билл, умер от рака легкого – результат выкуривания двух пачек сигарет в день на протяжении сорока лет. Скорбь его родителей была еще горше, потому что они пытались держать себя в руках. Но кто в таком случае может держать себя в руках? В «Отцах и детях» Тургенев описывает скорбь родителей Евгения просто, без прикрас и трогательно. По-настоящему трогательно.

16

11. Первым широко известным исследованием на тему скорби стала статья Эриха Линдеманна «Клиника острого горя» (Lindemann E. Symptomatology and Management of Acute Grief // American Journal of Psychiatry. Vol. 101. 1944. P. 141–148. Рус. пер.: Линдеманн Э. Клиника острого горя [1944] / под ред. В. К. Вилюнаса, Ю. Б. Гиппенрейтер // Э. Линдеманн. Психология эмоций. М.: Изд-во Моск. ун-та, 1984). Линдеманн включил в свой анализ так называемое предвосхищающее горе, подразумевая эмоциональную реакцию того, кто боится потерять любимого человека. Это единственное исключение из строгого правила о необратимости скорби.

17

6* Бранко Грюнбаум (1929–2018) – израильский и американский математик, один из создателей теории абстрактных многогранников.

18

7* Джоффри Шепард (1927–2016) – английский математик, доктор философии Бирмингемского университета.

19

1. Grünbaum B., Shephard G. Tilings and Patterns. New York: Freeman, 1987.

20

2. Доказательство того, что существует ровно семнадцать групп орнаментов, было представлено в статье: Фёдоров Е. С. Симметрия на плоскости // Записки Императорского Санкт-Петербургского Минералогического общества. Т. 28. СПб.: Типография Императорской Академии Наук, 1891. С. 345–390. Зачем нам нужно это доказательство? Не будь его, оставалась бы вероятность, что существует некая восемнадцатая группа орнаментов (узор замощения, предлагающий новую форму мозаики), скрывающаяся где-то в складках геометрии и доселе оставшаяся незамеченной.

21

3. Собор Благовещения Святой Марии в городе Ананьи (Италия) был построен в 1104 году. Внутренняя мозаика, включая узор из треугольников Серпинского, показанный на рисунке в тексте, была добавлена столетием позже. Этьен Гийон и Юджин Стэнли (Guyon E., Stanley H. E. Fractal Forms. Haarlem: Elsevier, 1991) привлекли внимание к фрактальным элементам мозаики. См. фото на: https://commons.wikimedia.org/wiki/File: Anagni_katedrala_04.JPG

22

4. Лучшее изображение картины «Лицо войны» вы можете увидеть в Википедии (https://en.wikipedia.org/wiki/The_Face_of_War) или на с. 97 книги Робера Дешарна «Дали» (Descharnes R. Dalí. New York: Abrams, 1985), которая также включает предварительный анализ этой картины.