
A Computer Called LEO: Lyons Tea Shops and the world’s first office computer
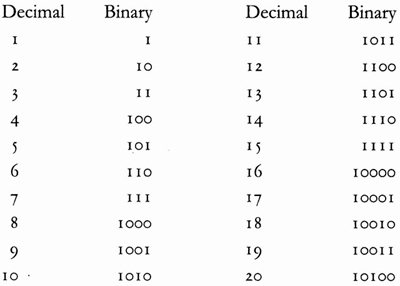
The advantage for computers of thinking in binary code is that their language consists of identical electrical pulses. At any point in a circuit, either there is a pulse, or there is not. On or off. 1 or 0. While a message written out in binary code might look extraordinarily cumbersome, it is in fact much quicker for a computer to work with instructions in this form than to incorporate some more complicated method of representing all the numbers and letters that human brains cope with quite happily.
In ENIAC, Eckert and Mauchly represented numbers in their conventional decimal notation. They used ten valves to represent a single digit: the fifth valve in a row of ten indicated the number five, and so on. Using binary code, just five valves would have been enough to represent all the numbers up to 31. To be fair to the Moore School designers, the theory of information processing based on binary digits, or ‘bits’ for short, was still being developed by Claude Shannon at Bell Labs when they began work on ENIAC. It has since been fundamental to the design of all modern computers.
Another major shortcoming of ENIAC was that it could not store programs. Mauchly had not taken the logical step that as programs consisted of information that could be represented digitally, they could be treated in the same way as data and stored in the computer itself. Each time ENIAC’s engineers wanted to run a new calculation they had to set up the program afresh by plugging wires into sockets, a process that could take a whole day.
The machine’s own builders realised that by the time they had it working, it was already obsolete. It deserves credit, however, for being the first to demonstrate publicly the power of electronic computing. It did work for the purpose for which it had been designed, and the army went on using it until 1955. Meanwhile, the publicity it attracted stimulated others to develop new avenues in the history of computing that would lead directly to the computers of today.
Among those who watched the building of ENIAC with interest was the Hungarian émigré mathematician John von Neumann. Von Neumann was by then an international star of mathematics, having established the mathematical foundations of quantum theory as well as developing the principles of game theory, which were to have a huge impact in economics, international relations, population biology and many other areas of modern experience. He was a founder member of the Institute for Advanced Study in Princeton, and had become an adviser to the army in 1940 when he joined the scientific advisory committee of its Ballistics Research Laboratory. Since 1943 he had also been attached to the Los Alamos atomic bomb project. At that time he was trying to model the explosion of the bomb mathematically and to predict the ensuing fireball, but had not been able to find any machine capable of crunching the numbers fast enough.
According to Herman Goldstine’s widely circulated account, it was his own chance meeting with von Neumann that first brought ENIAC to the renowned mathematician’s attention. One day in 1944 Goldstine looked up while waiting on a station platform for a train from Aberdeen to Philadelphia and saw von Neumann just a few feet away. Conscious of his lowly academic status but never one to miss an opportunity, he introduced himself and they fell into conversation. When the topic turned to ENIAC and what it would be able to do, Goldstine remembered, ‘the whole atmosphere changed from one of relaxed good humor to one more like the oral examination for the doctor’s degree in mathematics’.
A few months later von Neumann became a consultant to the Moore School team on the design of a successor machine that would avoid the serious shortcomings that had become apparent as ENIAC came into operation. Called the Electronic Discrete Variable Automatic Computer (EDVAC), it would handle data more economically by using binary rather than decimal digits and, most important of all, it would incorporate the means to store programs along with data.
In June 1945 von Neumann summarised these discussions in a memo, ‘A First Draft of a Report on the EDVAC’, formalising the logical design of such a machine. The report described the principles of an automatic, digital machine, consisting of five basic components: a memory, which stores both program and data; a control unit, which interprets the program; an arithmetic unit, which adds and subtracts data as directed by the program; and input and output units, which read in the program and data and deliver the final results. Computers with this design – and that includes the vast majority of modern computers – have ever since been said to have ‘von Neumann architecture’.
As in the case of Atanasoff and Mauchly, much ink and hot air has been expended over the injustice done to Eckert and Mauchly in denying them credit, especially for the stored program concept. Eckert had not only thought about this before John von Neumann joined the project; he had begun to design and build a prototype store. There was undoubtedly a conflict of interest between the academics von Neumann and Goldstine, who wanted to see the ideas in the EDVAC design incorporated as widely as possibly, and the engineers Eckert and Mauchly, who were thinking about capitalising on its commercial possibilities. The academics won hands down when Goldstine, apparently on his own initiative, distributed the report with von Neumann’s sole name on it to a couple of dozen carefully selected recipients. That was all it took to ensure that von Neumann’s name was permanently cemented to the concept of a stored program. Although EDVAC itself, eventually delivered to the Aberdeen Proving Ground in 1949, was not an especially significant machine, every subsequent computer designer was influenced by the contents of von Neumann’s report.
When Oliver Standingford and Raymond Thompson came to see him in 1947, Goldstine was back in academic life. His boldness in accosting John von Neumann on that station platform had paid off, and he was now working as his assistant on a new computer project at the Institute for Advanced Study. The two men found him in his office on the elegant, tree-shaded campus. His mood was relaxed and expansive. If he was surprised at being approached by representatives of a commercial company, far from the world of theoretical physics and higher mathematics that he inhabited, he gave no sign of it. He listened closely as the two men explained that they were exploring the possibility of using electronic calculators in the office. ‘That’s not a problem I’ve thought about before,’ began Goldstine. Thompson eagerly explained how much of the work of the Lyons clerks amounted to routine calculation, and how their whole approach to office systems was based on distilling useful information from the mass of data.
Goldstine instantly saw the point, and became tremendously enthusiastic. Sketching furiously on a yellow pad, he launched into a description of possible approaches to the problem given the technology that had been developed so far. At the same time he explained the advantages of electronic calculators of the type he was now working on over previous types of calculating machine. The most obvious was their speed of operation. While an IBM punched card tabulator could carry out the same processes of addition and subtraction, its speed was limited by the speed of its mechanical moving parts. The electronic calculator, in contrast, operated at the speed of an electron moving in space – in principle, each step in a calculation could be completed in less than a millionth of a second.
The real source of an electronic calculator’s power, said Goldstine, was its potential to store its own program along with interim and final results. It would operate automatically – there was little or no need for human intervention in the course of a run. While punched card machines could carry out as many parallel operations as there were columns on the card (the standard had increased from 40 to 80 since Hollerith’s time), most electronic computers operated serially, taking one instruction or piece of data from the store at a time. However, the gain in speed and the possibility of running a large number of different operations in a single program gave the electronic computer overwhelming superiority.
Goldstine finished by giving Thompson and Standingford a list of everyone he knew about in the United States who was doing serious work on electronic computing. Then, enjoying the astonishment of his listeners, he dropped his bombshell. ‘And, of course, there’s Professor Douglas Hartree in Cambridge, England.’
Hartree had recently been appointed Professor of Mathematical Physics at Cambridge University. Goldstine informed his astonished listeners that one of Hartree’s new colleagues was building a state-of-the-art computer in the Mathematical Laboratory there. The two men had come 3,000 miles to find out that a computer was already under construction a couple of hours’ drive away from Lyons’s headquarters. Goldstine warmly recommended that Thompson and Standingford should talk to Hartree about their ideas for a business computer. As soon as they had left, he sat down and dispatched a letter to Cambridge on their behalf.
With a much clearer understanding of the technology, and buoyed up by Goldstine’s enthusiasm, Thompson and Standingford then made a tour of every organisation on his list. They were not able to see ENIAC itself, which had been taken over by the army and was being rebuilt at their Aberdeen firing range. Permission initially granted was suddenly withdrawn on the grounds of confidentiality – but Goldstine said later that the army’s engineers had probably failed to get the notoriously unreliable machine working and were too embarrassed to admit it. At the Moore School itself, where ENIAC had been built in a spirit of adventure and enthusiasm, they found that the disbanding of the original team had left ‘a general air of apathy’. A smaller experimental calculator was built and working, but no one showed the smallest interest in their ideas on office computing.
Presper Eckert and John Mauchly, who had designed and built ENIAC, had left the Moore School a year earlier (following a dispute with Goldstine and von Neumann about the right to patent their invention) to form the Electronic Control Company. They, apparently alone among the early computer pioneers, planned to develop a computer for commercial production based on the EDVAC design, to be known as the Universal Automatic Calculator or UNIVAC. Naturally, a visit to their Philadelphia office was high on Thompson and Standingford’s list of priorities.
Eckert told them that he was talking to the Prudential Insurance Company of America about designing a machine to issue bills, and to carry out actuarial calculations. The big insurance companies had millions of policyholders and employed thousands of clerks to draft policies and send out bills for premiums. The office machinery suppliers had come up with some labour-saving devices for this kind of work, such as machines for printing frequently used addresses, but essentially the insurance business required heroic efforts of typing and filing. Prudential was the first and only example Thompson and Standingford came across of a company planning to use a computer for clerical work. A visit to its offices in Newark, New Jersey, revealed a company with an attitude as progressive as that of Lyons, though in a completely different line of business. It had a large Methods Division (comparable to the Systems Research Department at Lyons), with an innovator at its head, Dr Edmund C. Berkeley (later to become the author of the first popular computing book, Giant Brains). He was apparently confident that his company would have a machine installed and working within two years. In addition to preparing bills for insurance premiums, Berkeley planned to use the machine to prepare contracts, storing the 2,000 standard clauses and programming the machine to select those required in individual cases. This was the first Thompson and Standingford had heard of the possibilities computers offered for what we now call word processing. As things turned out, the Electronic Control Company was dogged by financial problems; in 1950 Prudential cancelled its contract with Eckert and Mauchly and later bought its first computer from IBM.
Extraordinary as it seems today, Eckert and Mauchly were out on a limb in perceiving a need for a general purpose commercial computer which could be produced for sale. The obvious candidates to pursue such a development were the existing office machine companies, who already had the customers and the sales forces to exploit a new market. Those that the Lyons pair visited, such as IBM, NCR and Burroughs, were secretive about their own research but they seemed to be more concerned to protect their traditional products than to develop entirely new ones. Standingford later wrote: ‘We were given a polite hearing, lunch and the sort of restrained reception reserved for the mentally unstable.’
It was a relief to have their confidence restored with a second visit to Goldstine. They found he had spent the intervening weeks thinking about the special requirements of office computing, and he gave them a detailed list of the components their computer would need. This time he took them to his engineering labs and showed them not only his partly built computer but prototype peripherals such as a device that would load programs and data into the machine through spinning magnetic wire (a forerunner of magnetic tape) from one reel to another. Profuse in their gratitude for Goldstine’s information and encouragement, Thompson and Standingford returned to New York and the boat home in a state of intellectual euphoria. Their minds were ablaze with the possibilities before them. While some might have used the cruise home, on the Queen Elizabeth, as an opportunity to relax, they lost no time in recording the knowledge and impressions they had gained in the first draft of the lengthy report on their visit they would be presenting to the Lyons board.
The first three sections of the report disposed of their visits to office machine companies and other businesses, concluding that Lyons’s methods were already so advanced that they had little to learn in this sphere. But Section D, headed ‘Electronic Machines in the Office’, stands as a prophetic document, showing both a firm grasp of the capabilities and limitations of the technology then developing, and a vision of where it all might lead. It was never published at the time, circulating only within Lyons, but in Britain at least no comparable account of the subject had ever been written.
Thompson and Standingford were unequivocal about their own enthusiasm for an electronic calculating machine. ‘Our object,’ they wrote, ‘in inquiring into the nature and possibilities of this machine was to find out whether it, or any adaptation of it, was capable of being put to use in commercial offices, and if this was not the case, to try to stimulate the development of such a machine.’ They went on to list the functions a computer might be capable of performing: storing data and instructions, performing sequences of calculations on stored material automatically, comparing words or figures in its memory and reacting to differences, and printing out results. They emphasised the astonishing speed at which these functions could be carried out, but showed how it posed a problem whose solution would later become the first priority in the development of the Lyons computer. ‘It is obviously wasteful to have a machine that is capable of working at these superhuman speeds,’ they wrote, ‘unless the information it is to work upon can be made available to it at relatively comparable speeds. The feeding clearly cannot be directly by clerks but mechanical and electrical means have been developed that are satisfactory.’
Thompson and Standingford recognised that what might be ‘satisfactory’ for a computer working on mathematical problems that might require minutes or hours of computation would not do in an office, ‘where the problem is to carry out a large number of simple operations’. This note of realism continued in an account of the importance of punching every input tape twice, using a device that compared the first and second versions to eliminate errors. The authors had clearly absorbed the philosophy that time on the computer was valuable, and everything possible had to be done to make sure that it was used efficiently.
After giving a short summary of the memory devices then under development, and an account of how a computer actually worked, Thompson and Standingford went on to suggest three examples of its applications in the office: sales invoicing, the typing of form letters and payroll. In each case, they explained, permanent information such as customers’ code numbers and addresses or employees’ names and rates of pay could be stored on magnetic wire or teleprinter tape and used again and again, while each week another input tape or wire would be prepared, giving hours worked, bonuses and so on. These two, together with an ‘instruction wire’ containing the program, would be played into the computer’s memory, the necessary calculation performed, and the computer would then print automatically the invoices, letters or payslips required.
Although almost all of their informants had been preoccupied with computers as mathematical tools, Thompson and Standingford were able to use their own background in systems research at Lyons to see how clerical tasks with rather little mathematical content, such as word processing and payroll management, could be recast as ‘calculations’ for the computer. It was a lateral step that hardly anyone, with the possible exceptions of Eckert and Mauchly and Edmund C. Berkeley at Prudential Insurance, had yet taken. All that now remained was to convince Simmons and the Lyons board that this was the way they should go in the future.
3 Made in Britain
It was predictable that Simmons and his colleagues should look to the United States for advances in technology, including computers. Its vast markets, coupled with a native enthusiasm for innovation, provided a fertile breeding ground for ideas and their commercial development. They did not know at that stage that the history of computing also owed much to British pioneers.
Charles Babbage (1792–1871), a showman as much as a thinker, had been in the forefront of the enthusiasm for scientific discovery and technological invention that ignited elements of London society in the first few decades of the nineteenth century. Although he had held the post of Lucasian Professor of Mathematics at the University of Cambridge for a number of years, he had spent very little time there. He was interested in everything, but his greatest concern was to subject the problems of society to scientific and preferably numerical analysis. He developed a passionate interest in factory management, and the studies he carried out predated by almost a century the ‘time and motion’ craze of the 1920s and 1930s. For example, in his 1832 book On the Economy of Machinery and Manufactures he published figures on the numbers of men, women and children needed to make pins, the time taken for each part of the process and the cost of each pin, taking into account labour and materials.
Writing of his search for laws and principles governing factory work, he commented: ‘Having been inclined during the last ten years to visit a considerable number of workshops and factories, both in England and on the Continent, for the purpose of making myself acquainted with the various resources of the mechanical art, I was insensibly led to apply to them those principles of generalisation to which my other pursuits had naturally given rise.’ From his observations he developed a poor opinion of the ability of the human species to undertake any repetitive work reliably. ‘One of the great advantages which we may derive from machinery,’ he said, ‘is from the check which it affords against the inattention of, the idleness or the dishonesty of human agents.’
The Industrial Revolution was in full swing. Machines spun and wove in factories at speeds unmatched by traditional cottage industry. Babbage the mathematician began to wonder if a machine could be made to do calculations. The best approach, he soon realised, was to reduce the calculation to a series of simpler stages, so that all the machine had to do was add and subtract. He owed this insight to the French mathematician Gaspard Riche de Prony, who had been charged with finding a feasible way to calculate all the new mathematical tables that would be needed following the introduction of the metric system by the French revolutionary government. De Prony’s solution was to organise a hierarchy of mathematical workers, beginning with a few professional mathematicians at the top and ending with a large team, who could add and subtract according to a formula worked out by those higher up the ladder. (The lowest tier was composed of redundant hairdressers, whose former customers had either lost their hair along with their heads, or prudently adopted a style of suitably radical simplicity.)
Babbage was convinced that anything a roomful of hairdressers could do, a machine could do better. He drew up designs for what he called his Difference Engine, and eventually persuaded the government to part with funds for its development. He got as far as producing a demonstration model that he displayed to wondering visitors in his London drawing room. It consisted of dozens of interconnected brass cogs with complex gears between them, which would perform predetermined (and apparently ‘miraculous’) procedures as he cranked a handle. The money ran out before he could produce a full-scale version. His design was vindicated when in 1991 curators at the Science Museum in London used his notes and drawings to produce his improved Difference Engine No. 2. Doron Swade, who led the project, tells the whole story in his book The Cogwheel Brain.
Money was not the only problem. Babbage had sidetracked himself by thinking up an even better machine: the Analytical Engine. Rather than setting up a calculation by positioning various cogs by hand, Babbage proposed to feed the Analytical Engine both program and data on punched cards such as those the French inventor Joseph Marie Jacquard had developed to automate the weaving of damask patterns into cloth. The machine never progressed beyond the design stage (although the design notes filled thirty volumes). But it encompassed much of the thinking behind the design of modern electronic computers: it had inputs, in the form of punched cards, a store or memory, a processing unit (which Babbage called the ‘mill’), and a variety of different outputs, including printed results or more card-punching.
The Analytical Engine also inspired a historic document, all the more remarkable in its day because the author was a woman. The document was entitled ‘Sketch of the Analytical Engine invented by Charles Babbage Esq.’ and published in Taylor’s Scientific Memoirs in September 1843. The ‘Sketch’ was originally written in French by the Italian engineer Luigi Menabrea. The English translation in the Memoirs, with the addition of extensive explanatory ‘Notes’, was by Augusta Ada, Countess of Lovelace, and only product of the short-lived marriage between the poet Lord Byron and Annabella Milbanke. Ada Lovelace, who was twenty-eight years old and a mother of three when the ‘Sketch’ was published, developed a passion for mathematical ideas at an early age. With all the emotional volatility of her father – although a cruelly restricted upbringing could have had as much to do with this as genetics – her own assessment of her mathematical gifts was sometimes unrealistic. But she formed a strong intellectual bond with Babbage, and proved an able advocate of his work. Her ‘Notes’ constitute the first accessible description of the capabilities and limitations of a computer. And a century before the sensational ‘electronic brain’ articles began to appear in the British and American press, she knew better than to oversell the discovery. ‘It is desirable,’ she wrote, ‘to guard against the possibility of exaggerated ideas that might arise as to the powers of the Analytical Engine … The Analytical Engine has no pretensions whatever to originate any thing. It can do whatever we know how to order it to perform … Its province is to assist us in making available, what we are already acquainted with’ (her italics). Today, when commentators frequently speculate that machine intelligence is on the verge of taking over from the human variety, her remark seems as percipient as ever.

