
Пособие для подготовки к успешной сдаче ЕГЭ по математике базового уровня в 2024 году
6.2. Примеры заданий и методика их выполнения
Пример 1 [3]Условие
Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице.
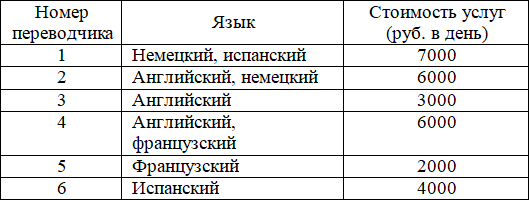
Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день.
В ответе укажите какой-нибудь один набор номеров переводчиков (без пробелов, запятых и других дополнительных символов)
Решение
Для решения данного задания необходимо собрать комплект из четырех переводчиков, при этом суммарная стоимость их услуг не должна превышать 12 000 рублей в день. Таким образом, переберем все возможные варианты:
• 1 (Немецкий, испанский), 3 (Английский), 5 (Французский): 7000 + 3000 + 2000 = 12000;
• 1 (Немецкий, испанский), 4 (Английский, французский): 7000 + 6000 = 13000;
• 2 (Английский, немецкий), 5 (Французский), 6 (Испанский): 6000 + 2000 + 4000 = 12000.
Другие комбинаций составить невозможно.
Очевидно, нам подходят комбинация 135 и 256. При этом ответ предполагает любую из данных комбинаций, также цифры могут быть тоже записаны в любом порядке.
Ответ: 135 < или > 153 < или > 315 < или > 513 < или > 531 < или > 256 < или > 265 < или > 526 < или > 562 < или > 625 < или > 652.
Пример 2 [3]Условие
В таблице приведены данные о шести чемоданах.
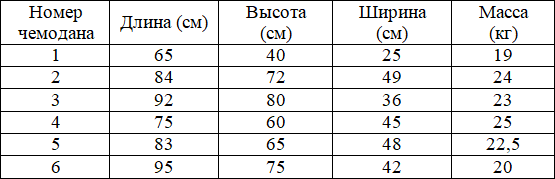
По правилам авиакомпании сумма трёх измерений (длина, высота, ширина) чемодана, сдаваемого в багаж, не должна превышать 203 см, а масса не должна быть больше 23 кг. Какие чемоданы можно сдать в багаж по правилам этой авиакомпании? В ответе укажите номера всех выбранных чемоданов (без пробелов, запятых и других дополнительных символов).
Решение
В первую очередь необходимо выбрать чемоданы, вес которых удовлетворяет условию, т.е., не больше 23 кг. Это чемоданы под номером 1, 3, 5 и 6. После чего выполним сложение их величин (длины, ширины и высоты) и сравним с числом 203:
Чемодан № 1: 65 + 40 + 25 = 130 < 203
Чемодан № 3: 92 + 80 + 36 = 208 > 203
Чемодан № 5: 83 + 65 + 48 = 196 < 203
Чемодан № 6: 95 + 75 + 42 = 212 > 203
Таким образом, нам подходят чемодан под номером 1 и 5.
Ответ: 15 < или > 51.
Пример 3 [3]Условие
Строительная фирма планирует купить 70 м3 пеноблоков у одного из трёх поставщиков. Цены и условия доставки приведены в таблице.
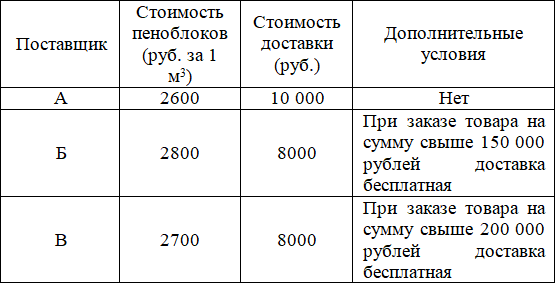
Сколько рублей нужно заплатить за самую дешёвую покупку с доставкой?
Решение
Поочерёдно вычислим сколько нужно будет заплатить каждому из поставщиков за 70 м3 пеноблоков:
Поставщик А: 2600∙70 = 182000
С учётом доставки: 182000 + 10000 = 192000
Поставщик Б: 2800∙70 = 196000
Доставка бесплатная, так как сумма товара свыше 150000
Поставщик В: 2700∙70 = 189000
С учётом доставки: 189000 + 8000 = 197000.
Очевидно, что самый дешёвый вариант – это заказать 70 м3 пеноблоков у поставщика А за 192000 руб.
Ответ: 192000.
Пример 4 [4]Условие
Рейтинговое агентство определяет рейтинг электрических фенов для волос на основе средней цены P (в рублях за штуку), а также показателей функциональности F, качества Q и дизайна D. Рейтинг R вычисляется по формуле
R = 3(F + Q) + D–0,01P.
В таблице даны цены и показатели четырёх моделей фенов.

Найдите наименьший рейтинг фена из представленных в таблице моделей.
Решение
Поочерёдно вычислим рейтинг каждого представленного в таблице фена:
Фен А: R = 3(3 + 4) + 2–0,01∙2100 = 23–21 = 2
Фен Б: R = 3(4 + 3) + 1–0,01∙2200 = 22–22 = 0
Фен В: R = 3(4 + 3) + 0–0,01∙2000 = 21–20 = 1
Фен Г: R = 3(2 + 4) + 1–0,01∙1700 = 19–17 = 2.
Наименьший рейтинг у фена Б, он равен 0.
Ответ: 0.
Задание 7. Анализ графиков и диаграмм
7.1. Общие вопросы
В спецификации контрольных измерительных материалов для проведения в 2024 году единого государственного экзамена по МАТЕМАТИКЕ (базовый уровень) в качестве проверяемого результата обучения применительно к заданию 7 указывается «умение оперировать понятиями: функция, непрерывная функция, производная, определять значение функции по значению аргумента; описывать по графику поведение и свойства функции».
Уровень сложности – базовый.
Максимальный балл за выполнение задания – 1.
Примерное время выполнения задания выпускником (мин.) – 7.
Чтобы решить задание 7 по математике базового уровня необходимо знать:
• что такое линейная функция и её график;
• что такое производная функции;
• геометрический смысл производной;
• как исследовать график функции.
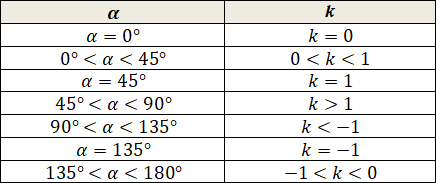
Линейная функцияЛинейная функция (прямая) имеет вид y = kx + b, где k – угловой коэффициент, который характеризует угол, который образует прямая y = kx + b положительным направлением оси Ох. Если k > 0, то этот угол острый; если k < 0, то – тупой; если k = 0, то прямая параллельна оси Ох или совпадает с ней.
Угловой коэффициент касательной равен тангенсу угла наклона касательной с положительным направлением оси абсцисс k = tg α, где α – угол наклона касательной.
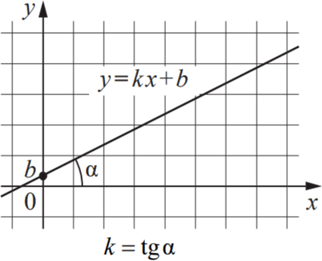
Также для удобства составим таблицу, которая будет демонстрировать зависимость коэффициента k от угла наклона прямой:
Производной функции в точке называется предел отношения приращения функции к приращению аргумента, если приращение аргумента стремится к нулю и если этот предел существует
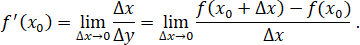
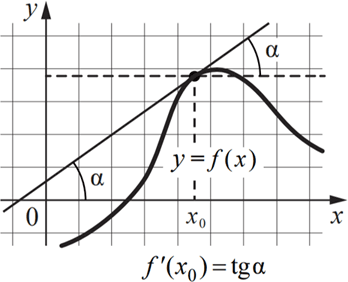
Знание углового коэффициента касательной к графику функции позволяет ответить на некоторые вопросы при исследовании функции.
Значение производной функции y = f(x) в точке x0 равно угловому коэффициенту касательной, проведенной к графику функции в точке с абсциссой x0:
f'(x) = k.
Если производная функции y = f(x) в точке x0 равна нулю, то касательная, проведенная к графику этой функции в точке с абсциссой x0, параллельна оси абсцисс или совпадает с ней. Так как угловой коэффициент касательной равен тангенсу угла наклона касательной с положительным направлением оси абсцисс k = tg α, то
f'(x0 ) = tg α.
Функция y = f(x) называется возрастающей на интервале (a;b), если для любых x1 и x2 из этого интервала таких, что x1 < x2, справедливо неравенство f(x1) < f(x2).
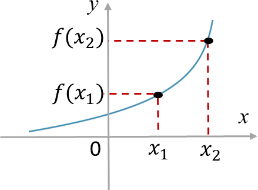
Функция y = f(x) называется убывающей на интервале (a;b), если для любых x1 и x2 из этого интервала таких, что x1 < x2, справедливо неравенство f(x1) > f(x2).
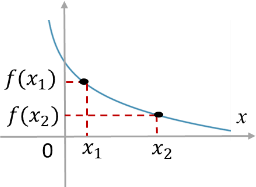
Точка xmax области определения функции называется точкой максимума, если для всех x из некоторой окрестности этой точки справедливо неравенство f(x) < f(xmax). Значение ymax = f(xmax) называется максимумом этой функции.
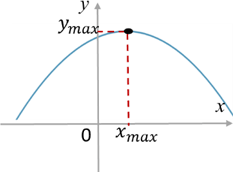
Точка xmin области определения функции называется точкой минимума, если для всех x из некоторой окрестности этой точки справедливо неравенство f(x) > f(xmin). Значение ymax = f(xmin) называется минимумом этой функции.
7.2. Примеры заданий и методика их выполнения
Пример 1 [4]Условие
На рисунках изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и значениями их производной в точке x = 1.
ГРАФИКИ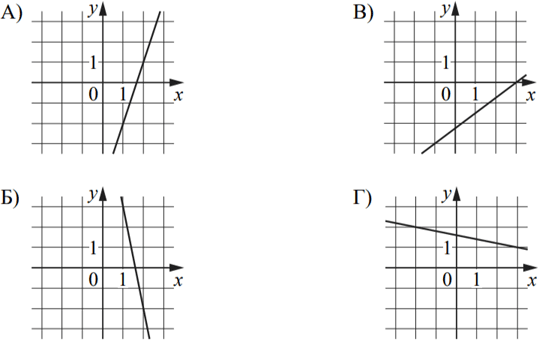
1) 0,75
2) –0,2
3) 3
4) –5
В таблице под каждой буквой укажите соответствующий номер.

Решение
Данное задание можно решить наглядно, найдя значение производной. Затем учесть, что оно равно угловому коэффициенту касательной, проведённой в этой точке. Так как угловой коэффициент касательной равен тангенсу угла наклона касательной с положительным направлением оси абсцисс k = tg α, то мы можем достроить все прямые до прямоугольного треугольника и найти тангенс угла наклона:
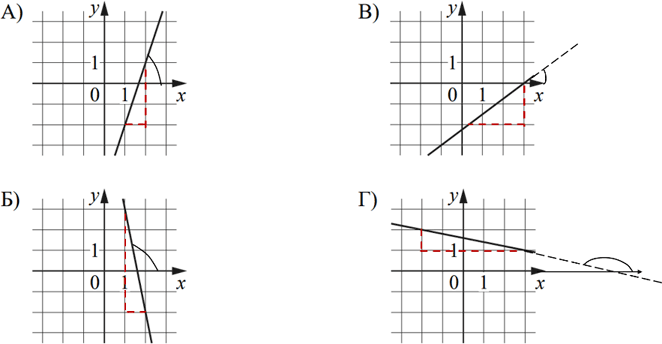
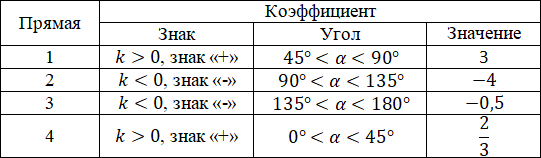
Так тангенс прямоугольного треугольника – это отношение противолежащего катета к прилежащему, найдем поочерёдно значение k для каждой из прямых:
А) k = 3/1 = 3, так как 45° < α < 90°, k < –1, следовательно k = 3
Б) k = 5/1 = 5, так как 90° < α < 135°, k < –1, следовательно k = –5
В) k = 3/3 = 0,75, так как 0° < α < 45°, k < –1, следовательно k = 0,75
Г) k = 1/5 = 0,2, так как 135° < α < 180°, – 1 < k < 0, следовательно k = –0,2
Заполним таблицу:
Ответ: 3412.
Пример 2 [3]Условие
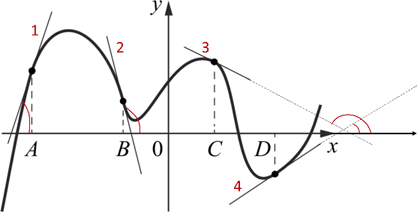
На рисунке изображены график функции и касательные, проведённые к нему в точках с абсциссами A, B, C и D.
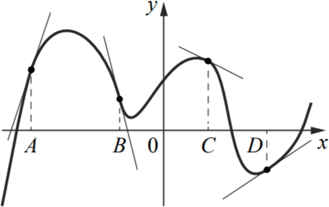
В правом столбце указаны значения производной функции в точках A, B, C и D. Пользуясь графиком, поставьте в соответствие каждой точке значение производной функции в ней.
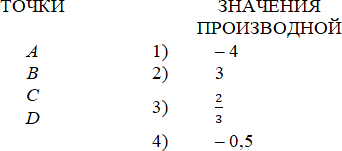
В таблице под каждой буквой укажите соответствующий номер.
Решение
Так как значение производной равно угловому коэффициенту касательной, проведённой в этой точке. Поэтому определим угловые коэффициенты для каждой из прямых. Для удобства пронумеруем их на рисунке и покажем угол наклона каждой прямой с положительным направлением оси Ox:
Составим таблицу, в которой определим коэффициент угла наклона каждой прямой
Заполним таблицу:
Ответ: 2143.
Пример 3 [3]Условие
Установите соответствие между графиками функций и характеристиками этих функций на отрезке [-1; 1].
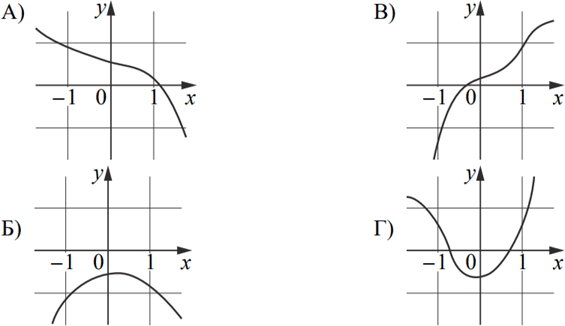
1) Функция имеет точку максимума на отрезке [1; 1].
2) Функция имеет точку минимума на отрезке [1; 1].
3) Функция возрастает на отрезке [1; 1].
4) Функция убывает на отрезке [1; 1].
В таблице под каждой буквой укажите соответствующий номер.

Решение
Рассмотрим подробнее каждую из представленных функций:
А) Данная функция убывает на отрезке [–1; 1], так как f(–1) > f(1).
Б) Данная функция имеет точку максимума на отрезке [–1; 1].
В) Данная функция возрастает на отрезке [1; 1], так как f(–1) < f(1).
Г) Данная функция имеет точку минимума на отрезке [1; 1].
Подтвердим данные отверждения дополнительными обозначениями на рисунке:
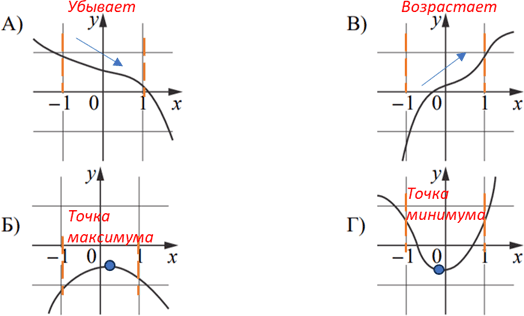
Заполним таблицу:
Ответ: 4132.
Пример 4 [3]Условие
На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси – температура двигателя в градусах Цельсия.
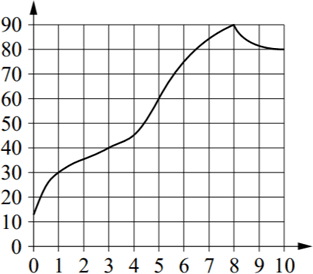
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.

В таблице под каждой буквой укажите соответствующий номер

Решение
При решении подобного задания будет удобно выделить на графике нужные интервалы, и посмотреть, то как ведет себя график на конкретном интервале:
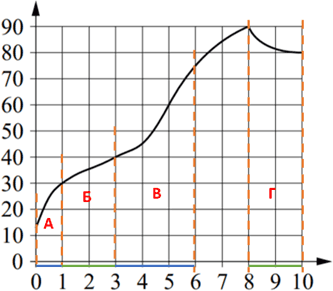
Таким образом, очевидно, что на интервале А температура не превышала 30°C, на интервале Б рост температуры был самым медленным, на области В температура находилась в пределах от 40°C до 80°C, а в области Г температура падала.
Заполним таблицу:
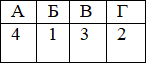
Ответ: 4132.
Задание 8. Анализ утверждений
8.1. Общие вопросы
В спецификации контрольных измерительных материалов для проведения в 2024 году единого государственного экзамена по МАТЕМАТИКЕ (базовый уровень) в качестве проверяемого результата обучения применительно к заданию 8 указывается «умение проводить доказательные рассуждения».
Уровень сложности – базовый.
Максимальный балл за выполнение задания – 1.
Примерное время выполнения задания выпускником (мин.) – 8.
Чтобы решить задание 8 по математике базового уровня необходимо уметь:
• внимательно читать вводную информацию, состоящую из двух или трех предложений;
• оценить правильность четырех высказываний, затем делать вывод.
Зачастую для более наглядного представления условия задачи рекомендую делать опорные рисунки.
8.2. Примеры заданий и методика их выполнения
Пример 1 [3]Условие
В классе учится 20 человек, из них 13 человек посещают кружок по истории, а 10 – кружок по математике. Выберите утверждения, которые верны при указанных условиях.
1) Каждый ученик этого класса посещает оба кружка.
2) Найдётся хотя бы двое учеников из этого класса, посещающих оба кружка.
3) Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике.
4) Не найдётся 11 человек из этого класса, которые посещают оба кружка.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Примечания
1
В дальнейшем КИМ ЕГЭю
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Всего 10 форматов