
История географических карт
Гекатей[7], самый молодой представитель милетской школы, выступил в защиту теории, в которой Землю в форме диска со всех сторон окружает океан, – несмотря на то, что он имел в своем распоряжении, как утверждалось, руководства по навигации, охватывавшие территорию от реки Инд до Красного моря; он знал о военном походе Дария в Скифию (513 г. до н. э.), а от торговцев и путешественников, которые бросали якоря в Милете, он, должно быть, слышал, что за горизонтом есть и кое-что кроме сжатого воздуха. Определенно ни один моряк того времени не стал бы выступать в защиту медлительного, «лениво текущего Океана», но похоже, что, путешествуя, мало что можно было узнать о Земле.
Первую робкую попытку приблизиться к истине в определении формы Земли предпринял Пифагор Иониец, основавший около 523 г. до н. э. в Кротоне философскую школу[8]. Имя Пифагора занимает в истории науки почетное место; ему приписывают несколько важных научных гипотез, которые впоследствии подтвердились. Возможно, самая важная из выдвинутых им теорий – это утверждение о том, что Земля представляет собой не плоскость и не диск, а шар. Как Пифагору удалось прийти к такому фантастическому выводу – краеугольному камню картографии, – загадка. По поводу рассуждений, которые помогли Пифагору выдвинуть такую теорию, позже выдвигались всевозможные предположения. Самый популярный вариант, который приписывали ему и последователи, и оппоненты, – утверждение, что Земля имеет форму сферы просто потому, что «сфера – самая красивая из объемных фигур». Некоторые другие авторы предпочитают думать, что Пифагор пришел к своему поразительному выводу путем наблюдения за небом и правильного объяснения того, что он там видел. Во всяком случае, пифагорейцы, развивавшие предложенные мастером идеи, выстроили вокруг своей сферической земли новую космическую систему; при этом они отвергли во многих отношениях все предыдущие концепции, включая и концепции самого Пифагора. Они оставили Землю сферической, но отказались от геоцентрической гипотезы, низведя Землю из положения центра Вселенной до статуса одной из планет – такой же, как Юпитер и Солнце. Затем они сконструировали систему, в которой небесные тела, включая Солнце, вращались вокруг некоего «центрального огня» таинственного происхождения. Логика, стоявшая за этим выводом, могла выглядеть примерно так: «Достойнейшее место надлежит занимать достойнейшему объекту, а огонь достойнее, чем земля…» Поэтому центральным телом Вселенной должен быть огонь, а не Солнце. Пифагорейцы ввели в систему еще одно небесное тело – антихтон, своего рода противоземлю. Это планета, которая находится на противоположной стороне вращающейся Вселенной и потому никогда не бывает видна с Земли. Некоторые авторитеты придерживались мнения, что в такой схеме Вселенной Земля остается неподвижной в пространстве; в то же время некоторые из пифагорейцев считали, что она обращается вокруг центрального огня по вытянутому кругу, так же как Солнце и Луна; в этом случае Земля должна была совершать один оборот вокруг центрального огня за день и ночь, или каждые двадцать четыре часа.
Прямоугольный мир Анаксимена (ок. 500 г. до н. э.) был водяным, но в пространстве его поддерживал сжатый воздух. Средиземное море омывало собственные берега, а за горизонтом несло свои волны великое кругоземное море Океан
Два ученых астронома, Евдокс и Каллипп, выдвигали сложные теории устройства Вселенной, куда входили системы концентрических сфер и невразумительные математические формулы. Эти теории не внесли в формирование картины мира ничего, кроме путаницы. Теории сами по себе были красивы, но Аристотель, рассматривая взгляды предшествовавших ему астрономов, счел необходимым значительно модифицировать их, а в некоторых случаях даже заменить собственными идеями. Вселенная, сказал он, конечна и имеет форму сферы. Звезды тоже круглые. Почему? Потому что природа ничего не делает просто так; поэтому природа дала звездам форму, меньше всего похожую на форму живых существ, у которых есть органы движения, – то есть форму, наименее подходящую для какого бы то ни было независимого движения. Он сказал, что Земля тоже круглая, несмотря на то что кое-кто возражал: не может быть, ведь линия горизонта, пересекающая встающее и заходящее солнце, прямая, а не изогнутая. Эта прямая на взгляд линия, рассуждал Аристотель, – оптическая иллюзия, вызванная огромной протяженностью горизонта и относительно небольшими размерами сферы восходящего или заходящего солнца; такое сочетание должно обманывать или, по крайней мере, сбивать наблюдателя с толку. Другие доводы, которые он приводил в пользу сферичности Земли, были понятнее и основывались на наблюдениях, которые любой человек может сделать невооруженным глазом. Во время частного лунного затмения, например, граница света и тени всегда округлая, вне зависимости от стадии затмения; с другой стороны, линия терминатора при разных фазах Луны может быть прямой или закругленной в любом направлении. Следовательно, затмение, вызываемое вмешательством Земли, доказывает, что она круглая. Второй аргумент Аристотеля оказался весьма ценным для развития картографии. Он указывает, что некоторые звезды, которые бывают видны над горизонтом в Египте и на Кипре, не видны севернее; более того, некоторые звезды, которые в этих местах заходят, в более северных всегда остаются над горизонтом. Учитывая эти факты, а также то, как заметно меняется горизонт при передвижении на небольшое расстояние, можно сделать вывод, что Земля должна иметь форму шара, причем не слишком большого шара.
Аристотель[9] не согласился с Фалесом в том, что Земля плавает в воде; он утверждал, что эта теория противоречит опыту. Мы видим, что вода может стоять на Земле или течь по ней, но мы никогда не видим, чтобы Земля плавала где бы то ни было. Он отверг и теорию, выдвинутую Анаксименом, Анаксагором и Демокритом, о том, что Земля, как плоская крышка или колесо фургона, висит в пространстве на подушке из сжатого воздуха. Аристотель пытался доказать, что Земля вообще не движется. Критикуя коллег, не согласных с этой идеей, он различал тех, кто ратовал за поступательное движение, и тех, кто считал, что Земля вращается вокруг оси, проходящей через полюса. О возможности двойного движения – обращения Земли внутри звездной сферы и вращения ее вокруг оси – не говорилось ничего.
Завершающим штрихом ранней философской астрономической системы, имевшей отношение к картографии, стала радикальная гипотеза «математика» Аристарха Самосского (ок. 310–230 гг. до н. э.). Аристарх, ученик астронома Стратона, в 288 г. до н. э. сменил Теофраста в качестве главы школы перипатетиков. Кроме теоретических данных первостепенной важности, он оставил потомству множество механических приспособлений. У Аристарха были многосторонние интересы, в частности его трактат «О размерах и расстояниях Солнца и Луны» во многих отношениях обогнал свое время. Он создал усовершенствованные солнечные часы, основание которых представляло собой не плоскость, а вогнутую полусферу, в центре которой был закреплен вертикальный указатель; направление и высоту Солнца при этом можно было определить одним взглядом. Он писал об оптике, свете и цвете. «И, – писал Хит, – нет ни малейшего сомнения, что именно Аристарх первым выдвинул гелиоцентрическую гипотезу. Древние свидетельства в этом смысле единодушны, а первым свидетелем может выступить Архимед, младший современник Аристарха, так что ошибка исключена». Более того, широкая публика не знает или не обращает внимания на то, что сам Коперник признавал, что эту теорию следует приписать Аристарху.
Говоря о Вселенной и о месте Земли в ней, Архимед писал: «Но Аристарх выпустил книгу о некоторых гипотезах, где получается, на основе сделанного допущения, что Вселенная во много раз больше, чем только что упомянутая «вселенная». Суть его гипотез в том, что неподвижные звезды и Солнце остаются на месте, а Земля обращается около Солнца по периферии круга, причем Солнце лежит в середине этой орбиты…» Второй свидетель Аристарха и его замечательного вклада в науку – Плутарх: «Только не надо, добрый друг, возводить на меня обвинение в нечестии, подобно Клеанту, который считал, что долг греков – осудить Аристарха Самосского по обвинению в нечестии за то, что он привел в движение Очаг Вселенной, причем то был результат его попытки «спасти явления» предположением, будто небо остается в покое, а Земля движется по наклонной окружности и в то же время вращается вокруг своей собственной оси». Современники действительно осудили Аристарха; мало кто в то время мог позволить себе отнестись к такой дикой гипотезе сколько-нибудь серьезно, и даже 1800 лет спустя, после того как Коперник сформулировал ее заново, она показалась убедительной лишь немногочисленным мыслителям-радикалам.
Как только гипотеза Пифагора получила общее признание и Земля обрела форму шара, за этим сразу же последовали попытки определить ее размер. Из ранних оценок самый большой размер Земля имела по оценке Платона, изложенной в его «Федоне», – по крайней мере, подразумевался самый большой размер. «Я считаю, – говорит Платон устами Сократа, – что Земля очень велика и что мы, обитающие от Геркулесовых столпов до реки Фазис, занимаем лишь малую ее частицу; мы теснимся вокруг нашего моря, словно муравьи или лягушки вокруг болота, и многие другие народы живут во многих иных местах, сходных с нашими…» Аристотель более консервативен и более конкретен. Он говорит, что наблюдения звезд доказывают, что Земля округла и не слишком велика. Он говорит также, что современные ему математики оценивали окружность Земли в 400 000 стадиев. (Примечание: для удобства читателей в этой книге все линейные величины, выраженные в стадиях, будут приведены в милях. 10 стадиев = 1 миля[10].) Архимед в своей книге «Об исчислении песчинок» говорит, что с тех пор эта цифра по всеобщему согласию была уменьшена до 30 000 миль. К тому моменту измерение окружности Земли стало среди ученых весьма популярным занятием, но много лет ничего не говорилось о методах, с помощью которых проводились подобные измерения.
Самое раннее достоверное описание метода, с помощью которого была впервые измерена Земля, относится к Эратосфену Киренскому (род. в 276 г. до н. э.). Это был человек разносторонних знаний, получивший прекрасное научное и философское образование. Эратосфен долгое время жил в Афинах, где его и нашел Птолемей Эвергет – правящий монарх Египта, искавший человека, который мог бы сменить Каллимаха на посту главы Александрийской библиотеки. Некоторые историки говорят, что Птолемей в то время искал еще и учителя для своего сына Филопатора (Птолемея IV). Однако если Эратосфен действительно принял на себя эти дополнительные обязанности, то, по всей видимости, его преподавание оказало не слишком большое влияние на наследника – правление свое тот начал с убийства собственной матери, да и в остальном внес немалый вклад в упадок династии.
Эратосфен писал по многим вопросам, как научным, так и философским, но самым выдающимся его вкладом в картографию стал правильный и логичный метод измерения размера Земли – классика в своем жанре и первый из множества описанных методов. Оригинальное описание, как и большинство трудов Эратосфена, утеряно, но благодаря астроному Клеомеду (ок. 50 г. до н. э.) нам известны и сам метод, и полученный с его помощью результат.
Метод Эратосфена базировался на нескольких известных или предполагаемых фактах: 1) что расстояние по прямой между Александрией и Сиеной (ныне Асуан) составляет 500 миль; 2) что Александрия и Сиена расположены на линии север—юг или, как формулирует это Клеомед, «на одном и том же меридиональном круге»; 3) что Сиена расположена на самом краю летней тропической зоны (то есть на тропике Рака) – факт, подтвержденный вроде бы Плинием, Аррианом и другими, так как в день летнего солнцестояния в Сиене солнце в полдень находится точно над головой; в этот момент гномон[11] не отбрасывает тени, а лучи солнца отражаются в воде на самом дне глубочайших колодцев. Далее, наблюдения показали, что в день летнего солнцестояния в Александрии полуденное солнце стоит не прямо над головой, а отбрасывает тень под углом равным одной пятидесятой части круга. Раз так, то и угловое расстояние между Александрией и Сиеной эквивалентно одной пятидесятой части длины земной окружности. Так что, если расстояние по прямой между двумя городами составляет 500 миль, то длина земной окружности окажется в пятьдесят раз больше, или 25 000 миль. Все настолько просто, что странно, как никто раньше до этого не додумался. Точность полученного результата зависит, конечно, от размера стадия как единицы измерения длины в то время, и похоже, что этот вопрос так никогда и не будет разрешен удовлетворительно для всех. Но если усреднить несколько разных величин стадиев, то окажется, что результат Эратосфена отличался бы от подлинной длины земной окружности всего на 200–300 миль, правда, если бы поверхность Земли была идеальной сферой. Это всеобщее и естественное убеждение, царившее до 1671 г.[12], было единственной теоретической ошибкой метода, использованного Эратосфеном; да и эту ошибку едва ли можно поставить ему в вину. Во всех остальных отношениях это был, по существу, тот же самый метод, которым пользуются для измерения Земли современные астрономы.
Что касается прочих ошибок, то они были вызваны неверной информацией, а та, в свою очередь, – традицией и всеобщими заблуждениями. Так, например, Сиена лежит не на тропике Рака, а на широте 24°5'30", то есть примерно в 37 милях к северу от тропика. Опять же, расстояние между Сиеной и Александрией составляло, по всей вероятности, не больше 453 миль. Сиена лежит не на меридиане Александрии, а в 3°3' к востоку от него. Разница в широте между Сиеной и Александрией, которую Эратосфен определил как одну пятидесятую часть большого круга, или 7°12' дуги, на самом деле составляет 7°5' дуги, что также дает ошибку в конечном результате. Представляется весьма вероятным, что Эратосфен догадывался о возможной неточности своего результата; он, по всей видимости, пересмотрел его в сторону увеличения и приравнял 25 200 милям. Это число хорошо делится на 360 частей, то есть на число градусов в большом круге; при этом каждый градус дуги равняется 70 милям. Если бы он остался верен первоначальной величине в 25 000 географических миль (250 000 стадиев), он оказался бы чрезвычайно близок к истине, так как окружность Земли по экватору очень близка к 25 000 английских миль – а именно 24 899, согласно измерению Гершеля. Очень неплохой результат для начинающего, у которого не было ни телескопа, ни – предположительно – вообще никаких точных инструментов.
Вторую зарегистрированную попытку измерить Землю предпринял Посидоний из Апамеи. Его результат был не слишком хорош, но он заслуживает места в нашей истории из-за смятения, которое вызвал среди ранних историков; кроме того, именно его результат, переданный Страбоном, а не результат, полученный Эратосфеном, несколько сотен лет считался общепринятым.
Посидоний (ок. 130—51 гг. до н. э.) был одним из наиболее образованных философов-стоиков. Прозванный Родосцем, он руководил школой на острове Родос, привлекавшей ученых со всех концов света. Хотя, как выразился один историк, Посидоний не был астрономом «в строгом смысле этого слова», его философия тем не менее охватывала не только астрономию, но и географию, математику и метеорологию; кроме того, он написал «Историю» в 52 книгах. В некоторых отношениях он превзошел астрономов – например, измеренное им расстояние от Земли до Солнца оказалось ближе к истине, чем величина, полученная Гиппархом. Его метод измерения Земли основывался на тех же общих принципах, что и метод Эратосфена, но, вместо вычисления разницы в высоте солнца в день летнего солнцестояния в двух разных местах, Посидоний использовал звезду. Клеомед в деталях описал эту историю следующим образом:
«В некоторых частях Греции невозможно увидеть яркую звезду Канопус, но на Родосе, где работал Посидоний, она поднималась достаточно, чтобы скользнуть по горизонту и тут же снова нырнуть обратно. В Александрии, еще южнее, высота Канопуса на меридиане равнялась «четвертой части «знака», то есть одной сорок восьмой части зодиакального круга. Конечно, это просто другой способ сказать, что разница в угловой высоте Канопуса в Александрии и на Родосе составляет 7°30'. Считалось, что линейное расстояние между этими двумя пунктами составляет 500 миль; таким образом, получаем окружность земли 48 х 500, или 24 000 миль».
Опять, использованный Посидонием метод был достаточно разумен, но результат получился ошибочным из-за неточных данных. Во-первых, угловое расстояние между Родосом и Александрией (то есть разница по широте) составляет не 7°30', а 5°15' – меньше одной шестидесятой части большого круга. Хит указывает, что ошибка определения высоты звезды по меридиану имела место, скорее всего, на Родосе, где эффекты рефракции на горизонте должны были серьезно затруднять наблюдения; другими словами, провести точное наблюдение звезды, едва-едва проскальзывающей по горизонту, очень трудно, если не невозможно. Вторая ошибка, расстояние в 500 миль между Александрией и Родосом, возникла в результате того, что оценивали расстояние моряки – люди, никогда не отличавшиеся тягой к преуменьшению. Расстояние оценивали по максимуму. Некоторые специалисты оценивали это расстояние в 400 миль, а Эратосфен, согласно Страбону, сказал, что оно не превышает 375 миль. Однако по оценке Посидония, которую привел Клеомед, окружность Земли все же составляла 24 000 миль. Она бы и осталась таковой, если бы не Страбон. Но, обсуждая последние опыты по измерению Земли, Страбон упоминает «того, который делает окружность Земли самой маленькой… а именно опыт Посидония, который оценивает ее окружность примерно в 180 000 стадиев [18 000 миль]…».
Откуда взялась такая огромная разница между величинами, приведенными Клеомедом и Страбоном? Хит предлагает остроумное объяснение, при котором оба источника оказываются в какой-то мере правы. Страбон, рассуждает он, склонен был верить Эратосфену и критически относился к общепринятому мнению по любому вопросу, не обязательно научному. Поэтому, переходя к расчетам и выводам Посидония, он отвергает общепринятую величину расстояния между Александрией и Родосом в 500 миль и использует вместо этого расстояние, названное Эратосфеном – 375 миль. В то же время оба автора, рассказавшие о Посидонии (и Клеомед, и Страбон), по всей видимости, согласны, что угловое расстояние между двумя пунктами составляет одну сорок восьмую часть меридионального большого круга. Теперь посмотрим: 48 раз по 500 миль составит 24 000 миль, а 48 раз по 375 миль – 18 000 миль. Если мы примем эти рассуждения, то придется сделать вывод, что или Клеомед, или Страбон, или оба автора работали только с изложением рассуждений Посидония, то есть с описанием его метода без числовых значений, и взяли на себя смелость добавить недостающие детали самостоятельно. Однако Страбон – всем историкам историк – привел меньшую из двух величин, и в результате общее признание получила длина земной окружности равная 18 000 миль. Соответственно один градус дуги считался равным 50 милям. Этим двум стандартам суждено было изменить ход истории и долгие годы причинять мучения многим поколениям географов.
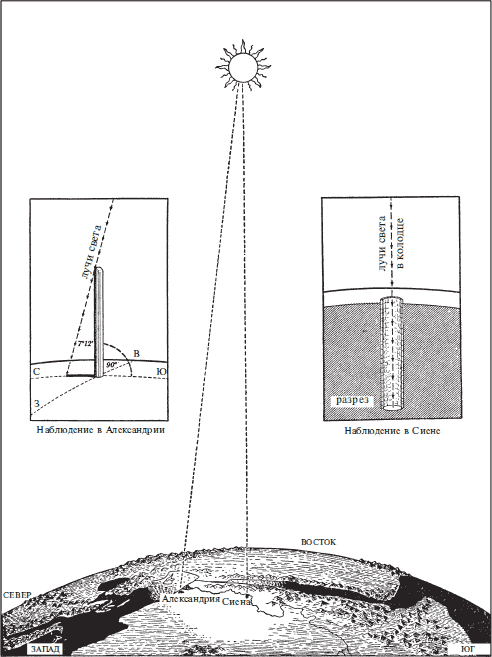
Самое раннее известное измерение окружности Земли провел Эратосфен около 240 г. до н. э. Его вычисления базировались на 1) угловой высоте солнца и 2) линейном расстоянии между Александрией и Сиеной
Обсуждая прогресс картографии, Страбон ссылается на карты, нарисованные «древними», но, следуя провозглашенному им самим принципу – игнорировать всех, кроме самых авторитетных из «современных» авторов, – он не говорит почти ничего, что могло бы указать нам, насколько на самом деле древни эти «древние». Он не называет никого из них по имени и вообще очень неопределенно говорит о развитии картографии до Гомера. Тем не менее изготовление карт – возможно, древнейшая разновидность примитивного искусства, поскольку с самого начала у этого искусства была цель. Это искусство столь же старо, как первые линии, проведенные человеком на песке или на стене пещеры. Более того, способность изобразить кусок земной поверхности – хотя бы небольшой – с помощью палочек и камешков или куска мела настолько универсальна, что, возможно, ее можно даже рассматривать как инстинктивную. Бесчисленные исследователи, имевшие дело с примитивными племенами, отмечали этот факт. Когда все остальные методы общения ничего не дают, на помощь приходит универсальный язык примитивной карты или схемы.
Самые ранние карты базировались на личном опыте и знакомстве с местностью. Они показывали путь через лес до соседнего племени; места, где можно обнаружить дичь, воду или соль; направление и расстояние до вражеских племен. Кочевой образ жизни несколько усложнял картину; бродячим племенам необходимо было знать, как пересечь пустыню и не умереть от жажды и как добраться домой за много миль после летнего выпаса скота. Чтобы начать войну – то есть приобрести землю этим древнейшим способом, – нужно было знать территорию соседей и хорошо в ней ориентироваться. Для торговли с другими племенами и народами нужны были еще большие знания о расстояниях и направлениях; чем дальше располагались рынки, тем точнее должны были быть к ним маршруты. По мере распространения цивилизации знания о расстояниях и направлениях приобретали все большее значение. Подобно записям ранних астрологов, географические описания и рисунки, рассказывающие, как добраться из одного места в другое, наносились – тем или иным способом – на камень, папирус или пергамент. Почти ничего из этих записей не сохранилось.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Примечания
1
Пергамент или папирус, который отскребли или отмыли от старых записей и использовали вновь (обычно при этом писали поперек прежних строк), называют палимпсестом. Существуют даже двойные палимпсесты – шкурки, которые использовали трижды. Поиск и исследование палимпсестов представляют собой высший пик библиографических изысканий, поскольку под верхними надписями на старых пергаментах было обнаружено несколько очень значительных рукописей, которые прежде считались утраченными; их удалось прочесть при помощи химикатов и инфракрасной лампы. Например, так называемый Ефремов кодекс представляет собой фрагменты греческого текста Ветхого и Нового Завета V в., поверх которых в XII в. были записаны сочинения Ефрема Сирина. (Здесь и далее примеч. авт.)
2
Вудс Роджерс (ум. в 1732 г.), морской капитан, одно время губернатор Багамских островов, вел весьма интересную жизнь. Некоторые из его биографов возражают против характеристики «пират», которую неизменно добавляли к его имени после грабительской экспедиции 1708—1709 гг., которой он командовал. Кроме общего командования, Роджерс быт еще и капитаном «Дюка» – одного из двух судов флотилии (второе судно назыиалось «Дучесс»). Эти два частных военный корабля снарядили бристольские купцы для действий против испанцев в южных морях. Штурманом на «Дюке» и лоцманом экспедиции быт Уильям Дампир, позже также завоевавший известность.
3
1 миля = 1,609 км.
4
Главный специалист по Страбону, его происхождению, воспитанию и образованию – сам Страбон. Все ссылки на Страбона в этой книге взяты из лондонского издания 1917 г. в восьми томах на английском языке.
5
Даты жизни Анаксимандра, по Аполлодору, – 611—547 гг. до н. э.
6
Анаксимен Милетский жил и работал во второй половине VI в. до н. э.
7
Гекатей, философ и историк, жил и работал в VI и V вв. до н. э.
8
Пифагор родился, по-видимому, на Самосе около 582 г. до н. э.
9
Аристотель (384—322 гг. до н. э.) родился в г. Стагира на побережье залива Стримоникас.
10
Современные эквиваленты древних мер длины всегда вызывали в научном мире серьезные разногласия. Аттический стадий удостоился особенно пристального внимания, но безрезультатно.
11
Г н о м о н – древнейший астрономический инструмент.
12
До экспедиции Жана Ришера в Кайенну в 1672 г. (см. главу VIII).