
Светлые века. Путешествие в мир средневековой науки

Рис. 1.3б. Звезды при наблюдении с экватора
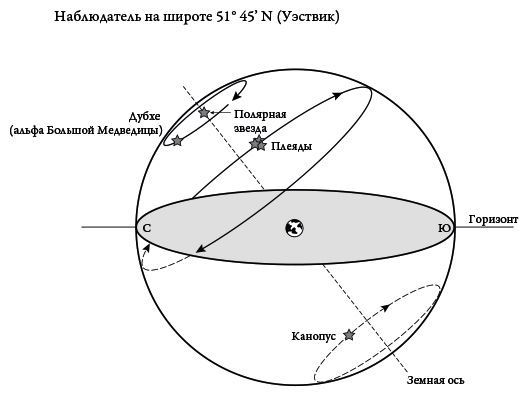
Рис. 1.3в. Звезды при наблюдении из Уэствика
Когда Вергилий писал о заходящих поутру Атлантидах, его читатели знали, что он имел в виду их первый утренний заход – поздней осенью, когда можно увидеть, как эти звезды скрываются за западным горизонтом как раз перед тем, как первые лучи Солнца должны были бы погасить их свет. Мы в Англии сохраняем наследие древней астрономии, называя самую знойную часть лета «собачьими днями»[48]. Астрономы прошлого привязывали этот период к первому появлению – незадолго до восхода Солнца в конце июля – Пёсьей звезды, Сириуса из созвездия Большой Пес, самой яркой звезды земного неба[49].
Средневековые звездочеты понимали эту механику небес – пусть они описывали годовой цикл, принимая за данность, что Солнце обращается вокруг Земли, а не Земля вокруг Солнца, это никак не влияло на наблюдаемое ими взаиморасположение небесных объектов. Глядя в небеса, не засвеченные уличными фонарями, они нетерпеливо ожидали возвращения знакомых созвездий. Легко представить себе, как Джон Вествик, проснувшись ясной ночью и дрожа от предрассветного холода, с надеждой ожидал появления горячих лучей Солнца, глядя в ту сторону, где, как он знал, должно было встать светило. И там, пока заря не затмила свет далеких звезд, он видел, как поворачивается небосвод и встают над горизонтом созвездия. Каждый день они выглядели немного по-другому. Эти звезды, последние глашатаи зари, разливающейся над церковью аббатства в День святого Луки в октябре, всего пару недель назад были еще совершенно не видны, потому что располагались слишком близко к Солнцу. Наблюдая звезды на рассвете и на закате, нетрудно было представить себе, как Солнце год за годом совершает один и тот же путь по созвездиям зодиакального круга, пока сами звезды стоят на месте на одном и том же угловом расстоянии друг от друга. Хотя в это время года Джон не мог видеть трапециевидную фигуру из четырех неярких звезд, составляющих созвездие Весы, он знал, что она располагается в День святого Луки прямо за Солнцем.
Итак, Солнце находилось в созвездии Весы; но в этот день в середине октября чаши этого созвездия уже не уравнивали время сна и бдения: осеннее равноденствие случилось несколько недель тому назад. Четырнадцатью веками ранее, когда Вергилий писал «Георгики», идею небесных Весов, уравновешивающих дневные и ночные часы, можно было понимать буквально, потому что Солнце вступало в это созвездие как раз в день осеннего равноденствия в сентябре. Но с течением веков созвездия медленно сдвигались к востоку. Пока Солнце скользило по своему извечному годовому кругу на фоне звездного занавеса, сам этот занавес тоже смещался к востоку. Скорость смещения составляет один градус в 72 года: недостаточно, чтобы один человек за время своей жизни мог этот сдвиг заметить, однако он не ускользнул от внимания древних и средневековых астрономов, продолжавших труды своих предшественников. Они назвали этот феномен «предварением равноденствий», потому что, как оказалось, равноденствия год от года наступают чуть раньше.
Астрономы немало потрудились, совершенствуя свои модели дрейфа так называемых неподвижных звезд. Их называли неподвижными, потому что созвездия сохраняли неизменную форму, в отличие от нескольких «блуждающих звезд», которые постоянно двигались по небесному своду и назывались греческим словом πλανήτης (планетес), что значит «странники». Самым простым решением проблемы медленного дрейфа созвездий было отделить видимые группы звезд от поименованных в их честь позиций, которые они некогда занимали на небосводе, хотя оно и вызывало путаницу, потому что и группы звезд (созвездия), и их старые позиции (знаки зодиака) сохраняли одно и то же прежнее имя. Поэтому в середине сентября в конце XIV века, когда день сравнялся с ночью, Джон Вествик увидел бы, что Солнце находится перед неизменной звездной фигурой Девы, но астрономы, его современники, знали, что знаком Девы называется тридцатиградусный сегмент неба к востоку от Солнца, находящегося в точке равноденствия.
В середине ноября, около Дня святого Мартина, Джон мог бы наблюдать утренний закат Плеяд и вслед за поэтом, приписавшим каждому месяцу свое занятие, посчитать это астрономическое событие сигналом к закалыванию свиньи: «В Мартынов день колю свинью». Монахи Сент-Олбанса именно так и считали. Тот же самый переписчик, что снимал копию с «Труда о земледелии», нарисовал и астрономический календарь с богато украшенными буквицами (рис. 1.4, 1.5). Инициалы KL, с которых начинался каждый месяц и которые служили рамкой, обрамлявшей сценку, символизирующую типичную для этого времени года работу, означают «календы», первый день месяца. Покладистую хрюшку, которую в октябре батрак тащит в лес, чтобы она покормилась желудями, в ноябре безжалостно закалывает бородатый йомен.

Рис. 1.4, 1.5. Календарь из Сент-Олбанса: начальные буквы как иллюстрации к октябрьским и ноябрьским трудам
Это было известно каждому, но формально никогда не закреплялось. На другом конце света все было иначе. В 1280 году в Китае придворный астроном монгольской династии Юань составил «систему определения сезонов» – календарь «Шоуши-ли». Монголы, завоевавшие Китай, со всей серьезностью отнеслись к обязанности императоров обеспечить население точным календарем и простым перечислением дней в году не ограничились. Государственная астрологическая комиссия привлекла десятки служащих – топографов и математиков – к составлению свода астрономических данных. Календарь задумывался как подспорье крестьянам при посадках и сборе урожая, а чиновникам должен был помочь определять даты государственных церемоний и принимать решения на основе астрологических карт, однако вне круга образованной элиты значительного следа не оставил[50].
Пусть сельское хозяйство в Сент-Олбансе велось не с такой астрономической точностью, жизнь монахов, разумеется, зависела от благополучия окрестных крестьянских хозяйств. И едва ли какое-то из них значило для монахов больше, чем некогда принадлежавшее аббатству владение Уэствик. В 1130 году щедрый до расточительности аббат Джеффри Горэм отдал его в приданое своей сестре, когда та выходила замуж. Поместье переименовали в Горэм, и этот факт еще долго не давал монахам покоя, не позволяя смириться с потерей. Тем не менее хронист из Сент-Олбанса по имени Матвей Парижский, известный безапелляционностью суждений, отзывался о Джеффри довольно мягко, воздавая должное достижениям Горэма, который активно перестраивал здания аббатства, расширял его владения, основал больницу и женский монастырь[51].
Джеффри – важная для нашего повествования фигура. Он мог бы стать первым из известных нам учителей той самой аббатской школы, где Джон Вествик постигал науку о числах, – если бы все-таки приступил к своим обязанностям. Еще не став монахом, Джеффри был учителем в Горроне, городе на севере Франции, и явно обладал кое-какой профессиональной репутацией. Его переманили в школу при Сент-Олбансе, когда аббатство решило поднять преподавание на новый уровень. Однако переезд затянулся, и монахи подыскали Горэму замену. Джеффри пришлось сводить концы с концами, преподавая в расположенном неподалеку городке Данстейбле. Коротая время в ожидании обещанного ему поста, Джеффри поставил на сцене мистерию, повествующую о жизни святой Екатерины (любимой святой нормандской королевской семьи)[52]. Подходящих для представления костюмов у него не было, и он позаимствовал несколько великолепных мантий у певчих Сент-Олбанса. Постановку ждал потрясающий успех. К несчастью, той же ночью пожар дотла спалил дом, где жил Джеффри. Огонь уничтожил все его книги и взятые взаймы дорогие мантии. Джеффри выплатил долг монастырю единственной собственностью, которая у него еще оставалась, – своей жизнью. Он предложил себя в жертву Богу и Сент-Олбансу, принял постриг и быстро поднялся до должности аббата. Матвей Парижский между делом замечает, что в качестве аббата Джеффри особенно заботился о сохранности одеяний монастырского хора[53].
Реформирование школы при Сент-Олбансе было продиктовано необходимостью привлекать в монастырь новых братьев. В 1370-х, когда Джон Вествик принял постриг, отбор был довольно жестким. В подборке типовых писем того времени сохранилось официальное уведомление, отправленное поручителю кандидата в монахи, провалившего испытательный срок, из чего понятно, что для поступления в монастырь требовались поручительства. Чтобы попасть в такое престижное место, как Сент-Олбанс, послушник как минимум должен был уметь читать и писать. Уровень грамотности в средневековой Англии был не настолько низок, как часто думают, – почти половина населения обладала базовыми знаниями и как минимум могла прочесть знакомую молитву. Но с Джона как с будущего монаха спрос был выше. Обучение в школе Сент-Олбанса не гарантировало сана, но было необходимым шагом на пути к нему[54].
При крупных аббатствах обычно создавались собственные школы, но школа Сент-Олбанса была в то же время и городской. Монах-летописец Матвей Парижский гордился тем, что «едва ли отыщешь в Англии школу лучше, или успешнее, или полезнее, или такую, что превосходит по числу учеников»[55]. Она располагалась сразу за стенами аббатства, и студенты, не принадлежавшие к монастырскому братству, могли учиться там платно. За бедными учениками, не имевшими возможности оплатить обучение, было зарезервировано 16 мест. Присматривал за такими учениками брат-попечитель (монах, отвечавший за благотворительную деятельность аббатства), столовались они также за счет монастыря. Согласно правилу, принятому в 1339 году, неимущие ученики должны были выбривать на голове тонзуру и ежедневно читать заутреню. Их учеба длилась «максимум пять лет, потому что этого времени достаточно, чтобы полностью овладеть грамматикой»[56].
Это была в буквальном смысле schola grammaticalis – грамматическая школа, как по названию, так и по стоявшим перед ней задачам. Единственным известным нам учебным пособием в ней были классические «Грамматические наставления» Присциана, учебник латинского языка, написанный в VI веке, а на экзаменах сдавали письмо и сочинение. Школа должна была готовить выпускников к монашескому служению, которое, кроме всего прочего, требовало умения читать и петь литургию. Однако переход из школы в монастырь совершался отнюдь не автоматически – по некоторым сведениям, в число неудачников попал даже Николас Брейкспир, будущий папа Адриан IV (1154–1159). Негарантированность результата вкупе с тем, что руководителям школ для увеличения дохода дозволялось принимать платных учеников сверх нормы, создавала запрос на качественное, всестороннее образование.
Серьезной научной подготовки в Сент-Олбанской грамматической школе Джон Вествик, скорее всего, не получил, но наверняка овладел как минимум азами арифметики, в том числе счетом и пониманием сути элементарных функций сложения и вычитания, деления и умножения. Никаких средневековых пособий для начинающих не сохранилось, но распространенные в монастырях учебники математики предполагали, что их читатели уже освоили базовый уровень.
Простые математические действия выполнялись в записи римскими цифрами; когда родился Джон Вествик, шел очень постепенный переход от этой системы к индо-арабским десятичным цифрам, которыми мы пользуемся сегодня. Цифры от 0 до 9 проникли на Запад только в XII веке[57]. То было великое время научного перевода, когда гуманитарии Испании и Южной Италии в ускоренном темпе перекладывали на латынь важнейшие арабские и греческие научные труды. Новые цифры значительно облегчали сложные астрономические и математические расчеты и постепенно прокладывали себе путь из Средиземноморья в Северную Европу. Огромную роль в популяризации арабских цифр сыграл итальянский математик Леонардо из Пизы, больше известный как Фибоначчи. Но английские монахи, которые с готовностью переняли десятичную систему счисления и обучали ей учеников, прекрасно знали, что пришла она с Востока, через исламские страны из Индии:
«Алгорисми говорит: когда я увидел, как индийцы записывают символ IX своими универсальными цифрами… я захотел узнать, как их можно использовать так, чтобы – с Божьей помощью – учиться было легче»[58].
Этим предложением открывается сочинение о новых цифрах, переписанное в XIII веке в аббатстве Бери-Сент-Эдмундс в Восточной Англии. Монах из Бери-Сент-Эдмундс написал его на латыни, но ему было отлично известно, что «Алгорисми» изначально создавал свой трактат на арабском языке. Автор оригинального арабского текста – увы, утерянного – энциклопедист IX века Мухаммад ибн Муса аль-Хорезми, жи вший в Центральной Азии. Аль-Хорезми познакомился с индийской арифметикой и принялся активно ее продвигать, когда работал в Багдаде, столице славного своими научными достижениями Аббасидского халифата. Делясь этими знаниями четыре столетия спустя, английский переписчик-бенедиктинец пунктуально зафиксировал их арабское и индийское происхождение.
Европа узнала о новых цифрах из текстов передовых для своего времени трактатов по теории чисел, которую средневековые переводчики на латынь в честь аль-Хорезми называли «алгорисмус»; отсюда произошло и современное слово «алгоритм»[59]. Преимущества применения новых цифр в сложных арифметических и геометрических вычислениях были очевидны, но стоит ли переключаться на новую систему в быту – было не совсем понятно. Хотя все числа в дошедших до нас рукописях Вествика – в обширных астрономических и тригонометрических таблицах, составленных им позже, – записаны цифрами, которые мы ошибочно называем арабскими, свои школьные математические упражнения он записывал римскими цифрами.
Принципиальное различие между римской и индо-арабской записью в том, что последняя приписывает каждому разряду определенное значение. Вес цифры зависит от ее места. В числе 21 цифра 1 означает «один», но в числе 12 она же означает «десять». С римскими цифрами все иначе, там I всегда означает «один», а Х – всегда «десять», и неважно, где цифра стоит: в конце (CIX) или в начале (XIII). Наша десятичная система – только одна из возможных форм позиционной системы счисления. Хотя цифры от 1 до 9 и знак пустого разряда 0 пришли из Индии V или VI века, сама концепция позиционной системы счисления гораздо старше и уходит корнями в вавилонскую, изобретенную где-то до 2100 года до н. э. Эта система счисления, унаследованная и частично перенятая у шумеров древними египтянами, греками и индийцами, была шестидесятеричной (sexagesimal – от латинского слова «шестьдесят»). Понимание шестидесятеричной системы важно для изучения средневековой математики и астрономии.
Вавилоняне записывали числа от 1 до 59 характерными клинообразными значками. (Чем больше было число, тем бóльшим количеством одинаковых значков оно обозначалось – в силу того, что эта система произошла от непозиционной системы счисления; однако читались числа как одно целое.) После 60 вавилоняне использовали те же значки, сдвигая их на шаг левее. Так, например, они писали наше 70 как 110 – для большей ясности мы можем добавить запятую, и тогда получится 1,10. Число слева от запятой – множитель 60. Дополнительная запятая отделяла бы следующий разряд шестидесяти. Число 2,21,40 содержит три разряда: 2 символизирует 2 х 3600, 21–21 х 60, а 40 – это 40 единиц. Соответственно число 2,21,40 в десятичную систему переводится следующим образом: (2 х 3600) + (21 х 60) + 40 = 8500. Система может показаться громоздкой, но вавилонянам было достаточно всего 14 символов, чтобы заставить ее работать, а это почти в два раза меньше, чем 26 символов современного английского алфавита[60].
Довольно странно наряду с десятичной использовать элементы и шестидесятеричной системы, но мы так и делаем, когда указываем время в часах, минутах и секундах. Моряки до сих пор определяют положение корабля в градусах, минутах и секундах (хотя в наши дни вместо секунд все чаще используют десятую часть минуты), потому что мы все еще держимся за шестидесятеричную систему счисления, унаследованную от вавилонских пионеров науки о времени и пространстве. Джон Вествик вычислял точное расположение планет именно в шестидесятеричной системе счисления.
Мы и сегодня записываем числа иногда словами (например, «десять» или «двадцать»), а иногда – римскими либо индо-арабскими цифрами, но читаем их всегда одинаково – так же поступал и Вествик, и его коллеги-монахи в XIV веке. Даже освоив индо-арабские цифры и шестидесятеричную запись, они не отказались от римских цифр. Безусловно, монахи оценили удобство десятично-шестидесятеричной системы для решения сложных математических задач, особенно если говорить о дробях, и понимали, какие возможности открывает перед ними ее приложение к более широкому кругу проблем, особенно в важнейшей математической науке – астрономии, где было принято делить небо на градусы и минуты. Однако римские цифры были понятными и привычными, что обеспечило им неувядающую популярность вне академического круга. Когда в 1440 году инок из Уоррингтона, городка на северо-западе Англии, взялся переводить с латыни на среднеанглийский язык руководство по изготовлению солнечных часов, он заодно перевел индо-арабские числа в римские[61]. Уверен, читатели оценили его заботу.
В 1396 году монахи Сент-Олбанса наконец исправили несправедливость длиной в две сотни лет, учиненную Джеффри Горэмом. Когда Джон Вествик родился, поместье Уэствик принадлежало графу Оксфорду, фавориту Ричарда II, но в 1388 году Безжалостный парламент осудил графа Роберта за измену и конфисковал его владения. Восемь лет спустя аббат Сент-Олбанса сговорился о покупке Уэствик-Горэма за 900 марок. Чтобы собрать такую внушительную сумму, пришлось скидываться, и хронист аббатства записал имена монахов и других благодетелей, которые внесли свою лепту. Он аккуратно отметил, какую сумму выделил каждый, – с помощью римских цифр:
«Предмет: получено в порядке дарения от братии и прочих как вспомоществование для покупки владения Уэствик, как то: в дар от владыки Николаса из Редклифа, архидьякона, XL марок. В дар от господина Роджера Хенрида, ризничего, VI фунтов XIII шиллингов IIII пенса. В дар от Томаса Сайдона, слуги аббата, VI фунтов XIII шиллингов IIII пенса…»
Список содержит имена 15 жертвователей и завершается следующими строками:
«В дар от Роберта Транча XI шиллингов & VIII пенсов.
Итого: L фунтов II шиллинга VIII пенсов»[62].
Здесь римские цифры используются вперемешку с чем-то довольно близким к позиционной системе счисления: фунтами, шиллингами и пенсами. (Вавилонская позиционная система счисления сложилась на базе единиц такого же типа, приспособившись к измеряемой величине.) В шиллинге было 12 пенсов, а в фунте – 20 шиллингов. Задача усложнялась тем, что деньги считали еще и в марках: одна марка составляла 2/3 фунта, или 13 шиллингов 4 пенса. Николас из Редклифа пожертвовал 40 марок, да и Роджер Хенрид и Томас Сайдон вряд ли намеревались внести в копилку непонятные 6 фунтов, 13 шиллингов и 4 пенса, а скорее всего, выделили круглую сумму в 10 марок. Хронист аббатства суммировал все эти марки, фунты, шиллинги и пенсы и пришел к верному результату (записав его римскими цифрами): 50 фунтов 2 шиллинга и 8 пенсов.
Если такие вычисления кажутся вам каким-то арифметическим подвигом, учтите, что до денежных реформ 1960-х и 1970-х годов школьникам всей бывшей Британской империи приходилось учиться складывать и вычитать двенадцатые и двадцатые доли фунтов, шиллингов и пенсов. (Чуть ли не весь остальной мир перешел на десятичную денежную систему еще в XIX веке.) Если немного попрактиковаться, сложению и вычитанию римских чисел тоже нетрудно научиться. Для начала можно представить себе X, десятку, как единицу – I, перечеркнутую линией, обозначающей, что перед нами сумма десяти таких единиц. V (пятерка) – это десятка (X), разделенная пополам горизонтально. Элементарное сложение, например VII + XVIII, нетрудно выполнить, записав все цифры рядом и переставив их для удобства местами: VIIXVIII превращается в XVVIIIII, а отсюда легко прийти к верному результату: XXV.
На самом деле подобные примеры можно решать и в уме. Для вычислений посложнее римские цифры переводили в более гибкий формат. В своем знаменитом трактате «Об исчислении времен» живший в VIII веке монах из Нортумбрии Беда Достопочтенный – выдающийся энциклопедист – знакомит читателя с двумя способами сделать это: греческая алфавитная система и метод, который он называл «очень полезным и простым умением счета на пальцах»[63].

Рис. 1.6. Положения пальцев при счете. Иллюстрация из трактата Беды «Об исчислении времен»
Как Беда и другие монахи считали на пальцах в десятичной системе? Вытяните руки перед собой, ладонями от лица (рис. 1.6). Начинать следует слева, с трех крайних пальцев левой руки. Эти три пальца, выпрямленные или полностью либо частично согнутые, показывают единицы от 1 до 9. Вот почему целые числа назывались digiti, что на латыни означает «пальцы»; отсюда и название цифровых технологий (digital)[64]. Степени десяти отсчитывали, по-разному сгибая и скрещивая большой и указательный пальцы (латинское слово «десять» – articuli – означает «костяшки»). За сотни отвечали большой и указательный пальцы правой руки, а за тысячи – средний, безымянный и мизинец. Таким образом, пальцами можно было показать любое число от 0 до 9999. Пальцам присваивалось конкретное разрядное значение – тысячам, сотням, десяткам и единицам было выделено определенное место, поэтому сложение и вычитание больших чисел трудности не представляли, более того, этим способом можно было даже решать простейшие примеры на умножение.
Самые маленькие числа откладывали на пальцах левой руки, и тому было две причины. Во-первых, в этом случае человек, который стоит к вам лицом, читает число как полагается, то есть слева направо. Жестовая арифметика служила не только для счета, но и для коммуникации. Жесты использовали на рынках, где шум и языковой барьер могли помешать разговору, или в монастырях, где нужно было соблюдать тишину. Беда даже предлагал использовать их в качестве алфавитно-цифрового кода, позволяющего передавать тайные сообщения. Во-вторых, если вы в своих вычислениях не выходите за сотню, правая рука остается свободной, и ею можно делать заметки, куда-то указывать или что-то в ней держать. Изумительно практичная система Беды пришла прямиком из классных комнат, где монахи учились использовать руки для запоминания музыкальной грамоты и определения дат или дней солнечного и лунного циклов.
Для простых вычислений было вполне достаточно пальцев, а вот для сложных использовали calculi – камешки или фишки. Джон Вествик учился работать с числами и наверняка мастерски пользовался абаком – счетной доской. Размещение камешков на расчерченной линиями доске представляло собой разложение числа на разряды. Некоторые разновидности абаков позволяли добавить промежуточную позицию для пяти единиц, пяти десятков, пяти сотен и так далее, и тогда фишек для счета требовалось меньше. В других разновидностях сами фишки были пронумерованы цифрами от 1 до 9, и тогда абак был просто рамкой, разделяющей разряды единиц, десятков, сотен и так далее. Монахи рисовали такие рамки в книгах и манускриптах, расчерчивая их на столбцы, которые часто стилизовали под колоннады своей обители, и раскладывали там счетные фишки. В промежутки между колонками они вписывали свои вычисления[65].
Абаками активно пользовались вплоть до Нового времени, несмотря на широкое распространение других, более совершенных техник счета. В сочинении «Жемчужина философии», популярнейшем учебнике, написанном картезианским монахом Грегором Рейшем и выдержавшем в XVI веке 12 изданий, раздел, посвященный арифметике, начинается с гравюры, иллюстрирующей два подхода к предмету (рис. 1.7). Слева – Боэций, позднеримский теоретик свободных искусств. Еще один энциклопедист (для средневековой науки всесторонне одаренные люди не редкость), Боэций писал труды по логике, музыке и арифметике, но наибольшую известность ему принесло «Утешение философией», размышление о природе человека. Книга оставила глубокий след в веках: только на английский язык ее переводили Альфред Великий, Джеффри Чосер и Елизавета I[66]. В этом сочинении Боэций, как многие астрономы до и после него, размышлял о необъятности Вселенной, космически малой величине Земли и холоде далеких звезд. Его присутствие на гравюре напоминает читателям, что математика – нечто большее, чем абстрактные величины.

Рис. 1.7. Арифметика. Фронтиспис четвертого тома «Жемчужины философии» Грегора Рейша (1503). Иллюстрация Альбана Графа

