
Алгоритмы для жизни: Простые способы принимать верные решения
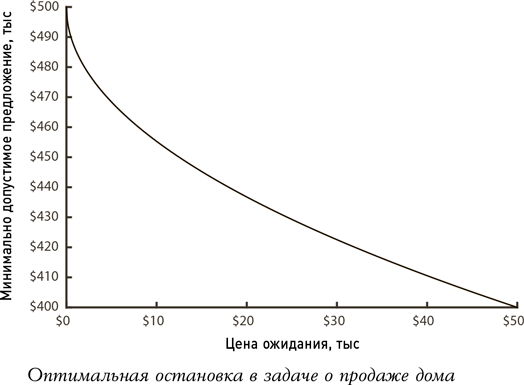
В данном примере важно отметить, что устанавливаемый нами предел зависит только лишь от стоимости поисков. Поскольку вероятность того, что следующее предложение окажется лучше предыдущего (а также стоимость выяснения этого) никогда не изменится, то нам нет смысла снижать стоп-цену, так как поиски продолжаются и не зависят от нашей удачливости. Мы устанавливаем ее однажды, прежде чем выставить дом на продажу, и в дальнейшем ориентируемся на нее.
Специалист по оптимизации Висконсинского университета в Мэдисоне Лора Альберт Маклей воспользовалась своими знаниями проблем оптимальной остановки, когда пришло время продавать ее собственный дом. «Первое же полученное нами предложение было замечательным, – рассказывает она, – но оно предполагало огромные затраты с нашей стороны, потому что покупатели просили нас съехать на месяц раньше, чем мы были к этому готовы. Было еще одно конкурентоспособное предложение… [но] мы держались, пока не получили подходящее нам». Многих продавцов необходимость отклонить парочку выгодных предложений весьма нервирует, особенно если последующие предложения уступают им в выгоде. Но Маклей твердо стояла на своем и сохраняла спокойствие. «Это было бы очень, очень тяжело, – признается она, – если бы я не знала, что математика на моей стороне».
Данный принцип применим к любой ситуации, где вам предстоит получить ряд предложений и заплатить за то, чтобы искать дальше или ждать следующего. Следовательно, это относится к случаям, которые выходят далеко за рамки продажи недвижимости. Например, экономисты, пользуясь этим алгоритмом, моделируют процесс поиска людьми работы и наглядно объясняют кажущийся на первый взгляд парадоксальным факт одновременного существования на рынке вакансий и безработных.
На самом деле, у этих вариаций проблемы оптимальной остановки есть еще одно поистине удивительное свойство. Как мы помним, возможность вернуть упущенный в прошлом шанс была жизненно важной в любовных поисках Кеплера. Но в случае с продажей дома или поисками работы вам никогда, ни в коем случае не следует так поступать, даже если есть возможность вернуться вновь к ранее отклоненному предложению и даже если это предложение все еще не утратило своей актуальности. Если оно не превышало ваш пороговый показатель на тот момент, оно не превысит его и сейчас. То, что вы заплатили за возможность продолжить поиски, – это невозвратные издержки. Не идите на уступки, не жалейте ни о чем. И никогда не оглядывайтесь.
Когда парковаться
Я пришел к выводу, что три главные административные проблемы в кампусе – это секс у студентов, спорт у выпускников и парковка у всего преподавательского состава.
Кларк Керр, президент Калифорнийского университета в Беркли (1958–1967)Еще одна сфера, где в избытке имеется проблема оптимальной остановки и где бессмысленно сожалеть об упущенном шансе, – это все, связанное с автомобилем. Автомобилисты уже фигурировали в упомянутой нами проблеме секретаря, а современный стиль жизни, побуждающий постоянно двигаться вперед, превращает каждую поездку на машине еще и в проблему остановки: поиски ресторана; поиски туалета и, что наиболее остро для городских водителей, поиски парковочного места.
Кто лучше расскажет обо всех тонкостях парковки, чем заслуженный профессор Калифорнийского университета в Лос-Анджелесе по градопланированию Дональд Шоуп, которого Los Angeles Times назвала рок-звездой парковки? Мы ехали к нему на встречу из Северной Калифорнии, заверив Шоупа, что оставили в запасе достаточно времени для непредвиденных проблем с трафиком. «Что до планирования непредвиденных проблем с трафиком, я думаю, что стоит планировать предвиденные проблемы», – парировал он. Шоуп прославился благодаря своей книге «Высокая цена бесплатной парковки», в которой он во многом внес ясность в процесс, который на самом деле имеет место, когда мы движемся из пункта А в пункт Б.
Бедного водителя стоит пожалеть! Идеальное парковочное место, в понимании Шоупа, – то, в котором умело соблюден точный баланс между стоимостью места парковки, неудобством от ходьбы пешком, временем, затраченным на поиски свободного пространства (сильно различается в зависимости от района, времени суток и т. д.), и сожженным за все это время бензином. Условия уравнения меняются с количеством пассажиров в автомобиле, которые могут разделить между собой плату за парковку, но не временем, потраченным на поиски места или на то, чтобы дойти пешком от места парковки до нужного пункта. Водитель должен учитывать, что пространство с наибольшим количеством свободных парковочных мест будет пользоваться наибольшим спросом. Поиски парковки всегда включают в себя элемент теории игр: пока вы пытаетесь перехитрить всех водителей на дороге, они, в свою очередь, пытаются перехитрить вас[5]. Таким образом, большинство проблем с парковкой сводится к одному фактору – уровню заполненности. Это отношение общего числа парковочных мест к количеству занятых в данный момент. Если уровень заполненности низкий, то можно без проблем найти хорошее место. Если же он высок, то поиск хоть какого-нибудь места, где можно было бы оставить машину, становится поистине сложной задачей.
Шоуп утверждает, что проблемы с парковкой возникли вследствие политики городских властей, которая привела к невероятно высокому уровню заполненности. Если плата за парковку в определенных районах слишком низкая (или – о ужас! – парковка и вовсе бесплатная), то большинство автолюбителей будет стремиться припарковаться именно там, а не чуть подальше, откуда придется немного пройти пешком. Таким образом, каждый старается встать там, но все места оказываются заняты, и люди в конечном счете тратят уйму времени и бензина, кружа по району в поисках парковочного места.
Решение Шоупа предполагает установку цифровых паркоматов, способных корректировать стоимость парковки по мере возрастания спроса (такой проект сегодня реализуется в центре Сан-Франциско). Цены устанавливаются исходя из уровня заполненности, и, по версии Шоупа, этот показатель должен быть в районе 85 % – довольно большой отрыв от 100 % забитых тротуаров большинства крупных городов. Он отмечает, что заполненность, возрастающая с 90 до 95 %, означает всего лишь на 5 % больше машин, зато удваивает количество времени, затрачиваемого водителем каждой из них на поиски места.
Ключевой момент влияния уровня заполненности на стратегию парковки становится очевиден, стоит нам только признать, что процесс парковки – это и есть проблема оптимальной остановки в чистом виде! Каждый раз, когда вы, проезжая по улице, видите свободное парковочное место, вам нужно принять решение: припарковаться здесь или проехать чуть ближе к конечному пункту и попытать удачи там?
Представьте, что вы едете по бесконечно длинной дороге, парковочные места на которой расположены через равные промежутки, и ваша цель состоит в том, чтобы свести к минимуму расстояние, которое вам придется пройти пешком от машины до конечного пункта. В этом случае решением станет правило «семь раз отмерь, один раз отрежь». Водитель, желающий найти оптимальный вариант парковки, должен проехать мимо всех свободных мест, находящихся дальше определенного расстояния от пункта назначения, а затем остановить свой выбор на первом же месте, которое встретится ему после этой точки отсчета. А вот расстояние, на котором «отмерь» превращается в «отрежь», зависит уже от соотношения мест, которые, вероятно, окажутся заняты, с общим их количеством – тот самый уровень заполненности. В таблице ниже приводятся расстояния для нескольких типичных соотношений.
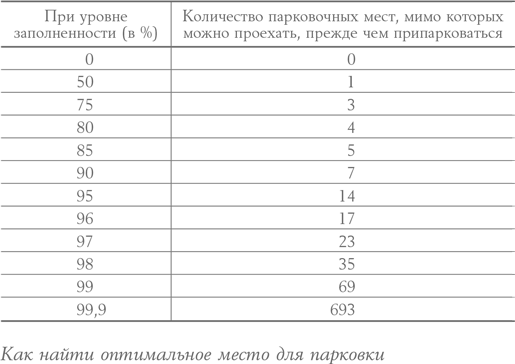
Если эта абстрактная бесконечная улица большого города имеет 99 %-ный уровень заполненности и всего 1 % свободных мест, то вам следует занять первое пустое место, которое попадется вам примерно за четверть мили до конечного пункта назначения (около 70 мест). Но если верить теории Шоупа, когда уровень занятости снизится до 85 %, вы можете не беспокоиться насчет парковки, пока вам не останется полквартала до места.
Но большинство из нас не катается по бесконечным прямым дорогам. Поэтому, как и в случае прочих проблем оптимальной остановки, исследователи рассмотрели ряд уловок. Например, они изучили стратегию оптимальной парковки в тех случаях, когда водитель может разворачиваться, когда чем ближе человек к месту назначения, тем меньше парковочных мест, и когда водитель составляет конкуренцию другим водителям, направляющимся в ту же точку. Но, каковы бы ни были условия задачи, наличие большего количества парковочных мест существенно облегчает жизнь. Это напоминание муниципальным властям: процесс парковки не так прост, как наличие ресурсов (мест) и обеспечение их максимального использования (занятость). Парковка – это процесс, который требует внимания, времени и затрат топлива и приводит к загрязнению окружающей среды и образованию заторов. Правильная политика решает эти проблемы. И, как ни парадоксально, наличие свободных мест в густонаселенных кварталах – признак того, что система функционирует правильно.
Мы поинтересовались у Шоупа, помогают ли ему его исследования в оптимизации его же собственных поездок на работу в Калифорнийский университет через все пробки Лос-Анджелеса. Вероятно, у лучшего в мире эксперта по парковке есть свои секретные приемы? «Все просто: я езжу на велосипеде», – ответил он.
Когда увольняться
В 1997 году журнал Forbes назвал Бориса Березовского самым богатым человеком в России; его состояние оценивалось примерно в $3 млрд. Всего десятью годами раньше он жил на зарплату сотрудника Академии наук СССР. Свои миллиарды он заработал на промышленных связях, появившихся у него в ходе исследований с целью основания компании-посредника между иностранными автоконцернами и советской автомобилестроительной компанией «АвтоВАЗ». Впоследствии компания Березовского стала крупным дилером машин «АвтоВАЗа» благодаря использованию схемы оплат в рассрочку, что в условиях гиперинфляции рубля имело огромное преимущество. На заработанные средства Березовский приобрел право на частичное владение «АвтоВАЗом», а затем вошел в совет директоров телеканала ОРТ и, наконец, компании «Сибнефть». Будучи представителем нового класса олигархов, он активно участвовал в политике, поддерживая перевыборы Бориса Ельцина в 1996 году и кандидатуру Владимира Путина в качестве его преемника в 1999 году.
Но в дальнейшем удача отвернулась от Березовского. Вскоре после избрания Путина на должность президента Березовский публично выступил против предложенных конституционных реформ, расширяющих президентские полномочия. Дальнейшие его публичные критические высказывания в адрес Путина привели к серьезному ухудшению их отношений. В октябре 2000 года, когда Путину был задан вопрос относительно критических замечаний Березовского, он ответил следующее: «Государство держит в своих руках дубину, которую применяют только один раз, но по голове. Пока государство эту дубину не использовало ‹…›. Когда мы серьезно рассердимся, мы, не колеблясь, применим ее…» Месяцем позже Березовский навсегда покинул Россию и эмигрировал в Англию, где продолжил критиковать режим Путина.
Вопрос, как вовремя уйти, когда ты на коне, анализировался в различных его проявлениях, но наиболее иллюстративным в ситуации с Березовским будет – да простят нас российские олигархи! – «задача грабителя». В этой задаче преступник может беспрепятственно совершить некоторое количество грабежей. Каждый из них сулит грабителю определенную выгоду, и каждый раз у него есть шанс эту выгоду получить. Но, если грабителя поймают и арестуют, он потеряет всю накопленную добычу. Каким алгоритмом ему стоит воспользоваться для максимизации своего ожидаемого дохода?
Тот факт, что данная проблема имеет решение, мало обрадует режиссеров фильмов об ограблениях: когда бандиты являются к старому гангстеру, отошедшему от работы, и уговаривают его в последний раз пойти на дело, хитрому вору остается только прикинуть числа. Тем более что результаты довольно наглядны: количество грабежей, которые вы хотите совершить, примерно равно шансам выйти сухим из воды, разделенным на вероятность быть пойманным. Если вы опытный вор и ваши шансы успешно провернуть дело равны 90 % (и 10 %, соответственно, вероятность его провалить), то стоит оставить свое ремесло после 90/10 = 9 грабежей. А неуклюжий новичок, чьи шансы на удачу 50/50? В первый раз вы ничего не потеряете, но не стоит искушать судьбу повторно.
Невзирая на опыт Березовского в решении задач оптимальной остановки, его история заканчивается весьма печально. Березовский умер в марте 2013 года; его тело было обнаружено телохранителем в запертой изнутри ванной комнате его дома в Беркшире. В официальном заключении патологоанатомического исследования сказано, что он покончил с собой – повесился, потеряв бóльшую часть своих богатств в результате ряда громких судебных процессов с участием своих врагов в России. Возможно, ему следовало остановиться раньше – накопив, к примеру, всего несколько десятков миллионов долларов и не влезая в большую политику. Но, увы, это было не в его правилах. Один из друзей Березовского, математик Леонид Богуславский, рассказал историю из времен их общей далекой юности о том, как они отправились на одно из подмосковных озер покататься на водных лыжах и у них сломался катер. Вот как Дэвид Хоффман описывает этот случай в своей книге «Олигархи»:
В то время как их друзья пошли разводить костер на пляже, Богуславский с Березовским отправились к причалу, чтобы попытаться отремонтировать мотор. ‹…› За три часа они полностью разобрали и заново собрали двигатель, но он так и не заработал. Друзья пропустили бóльшую часть пляжной вечеринки, но Березовский упорно не желал бросать попытки починить мотор. «Мы пробовали и так, и этак», – вспоминает Богуславский. Но Березовский не собирался сдаваться.
Как ни странно, это стремление никогда не сдаваться – во что бы то ни стало! – описывается и в материалах по проблеме оптимальной остановки. Возможно, это не выглядело очевидным в том широком спектре проблем, который мы рассматривали, но существуют последовательные задачи принятия решений, для которых правило оптимальной остановки не работает. Простой пример – игра «Утроить или потерять». Представьте, что у вас есть $1 и вы можете играть в эту игру бессчетное количество раз: поставьте на кон все деньги и получите 50 %-ный шанс утроить сумму и такой же 50 %-ный шанс все потерять. Сколько раз вам нужно сыграть? Несмотря на кажущуюся простоту, к этой задаче неприменимо правило оптимальной остановки, так как с каждой новой игрой ваш средний прирост становится чуточку выше. Начав с $1, вы в половине случаев получите $3, а в половине случаев – $0, так что в среднем вы ожидаете завершить первый раунд с $1,5 в кармане. Тогда, если в первом раунде вам повезло, появляется возможность во втором туре остаться либо с $9, либо с $0 – и средний выигрыш составляет уже $4,5. Математика утверждает, что вы всегда будете продолжать играть. Но если следовать этой стратегии, то в конечном итоге вы потеряете все. Некоторых проблем лучше избегать, нежели решать их.
Всегда останавливайтесь
Я проживу свою жизнь только единожды. Поэтому все то хорошее и доброе, что я могу сделать для ближних, я хочу сделать сейчас!
Я не хочу откладывать это или пренебрегать этим, потому что у меня не будет возможности пройти этот путь заново.
Стефан ГреллетНаслаждайтесь этим днем. Ведь вы не сможете забрать его с собой.
Энни ДиллардМы рассмотрели примеры конкретных людей, столкнувшихся в жизни с необходимостью решить проблему оптимальной остановки. Очевидно, что большинство из нас ежедневно встречается с этой проблемой в той или иной форме. Касается ли это секретарей, женихов (невест) или жилья, жизнь полна проблем оптимальной остановки. И главный вопрос заключается в том, действительно ли мы следуем наилучшей стратегии – благодаря эволюции, или образованию, или интуиции?
На первый взгляд, ответ – нет. Около дюжины исследований привели к такому результату: большинство людей, как правило, останавливаются слишком рано, оставляя лучшие варианты нерассмотренными. Чтобы глубже разобраться в данной ситуации, мы побеседовали с Амноном Рапопортом, профессором Калифорнийского университета в Риверсайде, который более 40 лет проводил эксперименты по оптимальной остановке.
Исследование, наиболее близкое к классической проблеме секретаря, было проведено Рапопортом и его соратником Дэррилом Сиэлом в 1990-х. В рамках этого исследования люди прошли через многократно повторяющиеся варианты проблемы секретаря, имея каждый раз от 40 до 80 претендентов на должность. Средний процент отсмотренных кандидатов, на котором поиски лучшего прекращались, составил 31 % – что довольно близко к оптимальным 37 %. Большинство руководствовались правилом «семь раз отмерь, один раз отрежь», но «отрезали» раньше, чем следовало, в четырех случаях из пяти.
Рапопорт признался, что он всегда помнит об этом, когда сталкивается с проблемами оптимальной остановки в повседневной жизни. В поисках квартиры, к примеру, он всегда борется с желанием поскорее заключить сделку. «Хотя по природе своей я очень нетерпелив и готов снять первую же квартиру, я стараюсь держать себя в руках!»
Но это нетерпение подводит нас к еще одному нюансу, который мы ранее не принимали во внимание в проблеме секретаря: роль времени. В конце концов, весь период, что вы ищете секретаря, у вас по факту нет секретаря! Более того, вы тратите дни на проведение собеседований вместо того, чтобы заниматься своей работой.
Этот вид расходов вполне объясняет, почему в процессе решения проблемы секретаря люди останавливаются в поисках раньше положенного срока. Сиэл и Рапопорт продемонстрировали, что если стоимость собеседования с каждым из кандидатов составит, предположим, 1 % от стоимости поиска лучшего секретаря, то оптимальная стратегия как раз совпадет с той, где люди перешли от слов к делу во время эксперимента.
Загадка в том, что в исследовании Сиэла и Рапопорта стоимость поисков не учитывалась! Так почему же все люди в лаборатории действовали как один?
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Сноски
1
В переводе М. Канна. – Прим. ред.
2
Жирным шрифтом выделены названия алгоритмов, которые будут описаны в книге.
3
В рамках этой стратегии существует 33 %-ная вероятность того, что мы откажем лучшему кандидату, и 16 %-ная вероятность – что мы никогда не встретим лучшего кандидата. Конкретно, есть шесть точных возможных последовательностей для трех кандидатов: 1–2–3, 1–3–2, 2–1–3, 2–3–1, 3–1–2, и 3–2–1. Если мы начнем отбор со второго претендента, то успех вероятен только в трех комбинациях из шести (2–1–3, 2–3–1, 3–1–2), соответственно в трех остальных случаях нас постигнет неудача – дважды из-за нашей излишней взыскательности (1–2–3, 1–3–2) и один раз по причине неразборчивости (3–2–1).
4
Необязательно строго 37 %. Точнее, математически оптимальная доля кандидатов, которых необходимо отсмотреть, рассчитывается по формуле 1/е (е – та же математическая константа, 2,71828…, которая появляется при расчете сложных процентов). Однако вам нет необходимости знать наизусть все 12 десятичных знаков числа е. На самом деле любое значение от 35 до 40 % максимально приближает вас к успеху.
5
Более подробно вычислительные риски теории игр рассматриваются в главе 11.
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Всего 10 форматов