Математика космоса: Как современная наука расшифровывает Вселенную

На протяжении долгого времени научным наследникам Ньютона приходилось производить все вычисления вручную – и во многих случаях это была поистине героическая задача. Яркий пример такого рода – Шарль-Эжен Делоне, который в 1846 году начал вычислять приближенную формулу движения Луны. На это у него ушло более двадцати лет, а результаты пришлось публиковать в двух томах. В каждом из этих томов более 900 страниц, и весь второй том занимает собственно формула. В конце XX века результат Делоне удалось проверить с применением компьютерной алгебры (программных систем, способных манипулировать не только числами, но и формулами). Было выявлено всего две небольшие ошибки, одна из которых является следствием другой; суммарный эффект от обеих ошибок пренебрежимо мал.

Законы движения и гравитации – это законы особого рода, законы, выражаемые так называемыми дифференциальными уравнениями. Такие уравнения задают скорость, с которой те или иные величины изменяются с течением времени. Скорость – это быстрота изменения положения тела; ускорение – это быстрота изменения скорости. Знание скорости, с которой в настоящее время изменяется та или иная величина, позволяет вам спроецировать эту величину в будущее. Если машина едет со скоростью 10 метров в секунду, то через секунду она сдвинется на 10 метров. Однако для того, чтобы считать таким способом, нужно, чтобы скорость была постоянной. Если же машина ускоряется, то за секунду она отъедет от вас более чем на 10 метров. Чтобы обойти эту проблему, в дифференциальных уравнениях указывается мгновенная быстрота изменения. По существу, они работают с очень короткими промежутками времени, так что быстроту изменения на этом промежутке можно считать постоянной. На самом деле математикам потребовалось несколько столетий, чтобы довести эту идею до полной логической строгости, поскольку никакой конечный интервал времени нельзя считать мгновенным, если он не равен нулю, а за нулевой интервал времени ничто не меняется.

Компьютеры произвели в этом деле настоящую методологическую революцию. Вместо расчета приближенных формул движения, а затем подстановки чисел в эти формулы теперь можно с самого начала работать с числами. Предположим, вы хотите предсказать, где некоторая система тел – скажем, спутники Юпитера – будет находиться через сто лет. Начните с первоначальных позиций и параметров движения Юпитера, его спутников и всех остальных тел, которые могут иметь значение, – в данном случае это Солнце и Сатурн. Затем, постепенно, один крошечный временной шаг за другим, вычисляйте, как изменяются числа, описывающие все задействованные тела. Повторяйте это действие до тех пор, пока не дойдете до временной отметки сто лет. Стоп. Человек, проводящий вычисления при помощи карандаша и бумаги, не смог бы воспользоваться этим методом для расчета сколько-нибудь реалистичной задачи. На это потребовалось бы несколько жизней. Однако при наличии быстрого компьютера метод становится вполне реализуемым, а современные компьютеры очень и очень быстры.

Откровенно говоря, все не настолько просто. Притом что ошибка на каждом шаге (вызванная тем, что мы считаем быстроту изменений постоянной, хотя на самом деле она успевает немного измениться) очень мала, шагов вам придется сделать ужасно много. При многократных операциях с маленькой ошибкой на каждом шагу результирующая ошибка не обязательно получится маленькой, но тщательно продуманные методы позволяют удержать ошибки под контролем. Именно на это нацелена целая область математики, известная как численный анализ. Удобно называть такие методы «моделированием», что отражает принципиальную роль в них компьютера. Важно понимать, что невозможно решить задачу, просто «засунув ее в компьютер». Кто-то должен запрограммировать машину, задать ей математические правила, которые обеспечат близость вычислительных результатов к реальности.

Правила, о которых идет речь, настолько точны, что астрономы могут предсказывать затмения Солнца и Луны с точностью до секунды, а положение планеты с точностью до нескольких километров на сотни лет вперед. Подобные «предсказательные» расчеты можно проводить и назад во времени, чтобы можно было точно определить, когда и где произошли известные нам по историческим хроникам затмения. Эти данные используются, к примеру, для датирования наблюдений, сделанных тысячи лет назад китайскими астрономами.

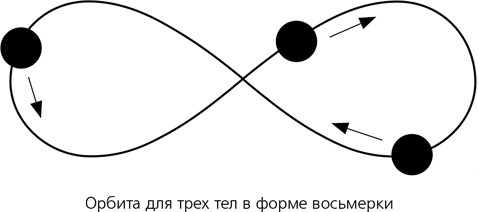
Даже сегодня математики и физики продолжают открывать новые неожиданные следствия из закона всемирного тяготения Ньютона. В 1993 году Крис Мур при помощи численных методов показал, что три тела с идентичными массами могут вечно гоняться друг за другом по одной и той же орбите в форме восьмерки, а в 2000-м Карлес Симо также численно показал, что эта орбита стабильна с точностью, возможно, до медленного дрейфа. В 2001 году Ален Ченсинер и Ричард Монтгомери привели строгое доказательство существования такой орбиты на основе принципа наименьшего действия – фундаментальной теоремы классической механики. Симо открыл множество подобных «хореографий», в которых несколько тел одинаковой массы преследуют друг друга, двигаясь все время по одному и тому же (сложному) пути.

Орбита в форме восьмерки для трех тел, судя по всему, сохраняет стабильность и при слегка различных массах тел, что открывает небольшую вероятность того, что где-то во Вселенной три реальные звезды могут вести себя таким замечательным образом. Согласно оценкам Дугласа Хегги, по одной такой тройной системе может приходиться на каждую галактику, а уж вероятность существования во Вселенной хотя бы одной такой системы довольно значительна.

Все эти орбиты существуют на плоскости, но есть уже и новый трехмерный вариант. В 2015 году Юджин Окс догадался, что необычные орбиты электронов в «ридберговских квазимолекулах», возможно, тоже существуют по законам Ньютоновой гравитации. Он показал, что в системах двойных звезд могут существовать планеты, двигающиеся от одной звезды к другой и обратно по спиральной орбите, обвивающей соединяющую эти звезды линию. В середине витки спирали лежат свободнее, к звездам на концах – плотнее. Представьте себе, что вы протягиваете между звездами пружинку игрушку-слинки, растянутую посередине и свернутую в петли на концах. Для звезд с разными массами пружинка должна сужаться от одного конца к другому, как конус. Подобные орбиты могут быть стабильными, даже если звезды движутся не по окружностям.

Коллапсирующие газовые облака порождают плоские орбиты, поэтому образование планет на описанных выше орбитах маловероятно. Но планета (или астероид), оказавшаяся в результате возмущения на сильно наклоненной орбите, может в редких случаях быть захвачена двойной звездой и в результате оказаться на спиральной орбите между ними. Некоторые данные указывают на то, что Kepler-16b – планета, обращающаяся вокруг одной далекой звезды, – может относиться к этой редкой категории.

Следует отметить, что один из аспектов закона всемирного тяготения немало беспокоил великого автора; по существу, он беспокоил автора закона сильнее, чем большинство его последователей. Как известно, закон описывает силу, с которой одно тело действует на другое, но ничего не говорит о том, как эта сила работает. Закон просто постулирует загадочное «дальнодействие». Когда Солнце притягивает Землю, Земля каким-то образом должна «знать», как далеко она находится от Солнца. Если бы, к примеру, оба объекта соединяла какая-то эластичная веревочка, то эта веревочка могла бы передавать воздействие; тогда величину силы определяли бы физические характеристики связи. Но между Солнцем и Землей нет никакой материальной связи, одно только пустое пространство. Как же Солнце узнает, с какой силой надо тянуть Землю, и как Земля узнает, с какой силой ее тянут?[10]

С практической точки зрения мы можем применять закон всемирного тяготения, не тревожась о том, посредством какого физического механизма сила передается от одного тела другому. Вообще говоря, все именно этим и занимаются. Однако некоторые ученые обладают отчетливой философской жилкой; самый яркий пример – Альберт Эйнштейн. Его специальная теория относительности, опубликованная в 1905 году, изменила представления физиков о пространстве, времени и веществе. Расширение этой теории в 1915 году до общей теории относительности изменило также их представления о гравитации – и, как бы между прочим, разрешило щекотливый вопрос о том, как сила может действовать на расстоянии. Для этого общая теория относительности, собственно говоря, избавилась от силы.

Эйнштейн вывел специальную теорию относительности из одного-единственного фундаментального принципа: скорость света[11] остается неизменной, даже если наблюдатель сам движется с постоянной скоростью. В Ньютоновой механике, если вы находитесь в отрытом автомобиле и бросаете вперед по ходу движения мяч, то скорость мяча, измеренная неподвижным наблюдателем на обочине, будет равна скорости мяча по отношению к автомобилю плюс скорость автомобиля. Аналогично, если вы будете светить фонарем вперед по направлению движения, то скорость света, измеренная человеком на обочине, должна, по идее, равняться обычной скорости света плюс скорость автомобиля.

Экспериментальные данные и кое-какие мысленные эксперименты убедили Эйнштейна, что со светом все иначе. Наблюдаемая скорость света одинакова как для человека, светящего фонарем вперед, так и для человека на обочине. Логические следствия из этого принципа, который, как мне всегда казалось, следовало бы назвать принципом безотносительности, поражают воображение. Ничто не может двигаться быстрее света[12]. По мере того как тело приближается к скорости света, оно сжимается в направлении движения, его масса увеличивается, а время для него течет все более медленно. При скорости, равной скорости света, – если бы такое было возможно – тело стало бы бесконечно тонким и бесконечно тяжелым, а время для него остановилось бы. Масса и энергия связаны между собой: энергия равна массе, умноженной на квадрат скорости света. Наконец, события, которые один наблюдатель видит происходящими одновременно, могут оказаться неодновременными для другого наблюдателя, который движется с постоянной скоростью относительно первого.

В Ньютоновой механике никаких таких странностей нет. Пространство есть пространство, а время есть время, и вместе им не сойтись. В специальной теории относительности пространство и время до некоторой степени взаимозаменяемы, причем степень этой взаимозаменяемости ограничивается скоростью света. Вместе пространство и время образуют единый пространственно-временной континуум. Несмотря на странные предсказания, специальная теория относительности получила признание как наиболее точная теория пространства и времени из всех, какие у нас имеются. Большая часть наиболее парадоксальных эффектов в ней проявляется лишь тогда, когда объекты движутся очень быстро; вот почему мы не замечаем их в повседневной жизни.

Самый очевидный недостающий ингредиент в этой теории – тяготение. Эйнштейн много лет пытался встроить силу тяготения в теорию относительности; отчасти его подталкивала к этому известная аномалия в орбите Меркурия[13]. Конечным результатом этих попыток стала общая теория относительности, распространившая выводы специальной теории относительности с «плоского» пространственно-временного континуума на «искривленное». Мы можем приблизительно представить себе, о чем идет речь, если сократим пространство до двух измерений вместо трех. При этом пространство станет плоскостью, а специальная теория относительности будет описывать движение частиц на этой плоскости. В отсутствие гравитации они движутся по прямым линиям. Как указывал Евклид, прямая есть кратчайшее расстояние между двумя точками. Чтобы ввести в картину гравитацию, поместим на плоскость звезду. Частицы теперь уже не будут двигаться по прямым линиям; вместо этого они начнут огибать звезду по криволинейным траекториям, таким как эллипсы.

В Ньютоновой физике эти траектории искривлены потому, что некая сила отклоняет частицу с прямого пути. В общей теории относительности аналогичный эффект достигается искривлением пространства-времени. Предположим, что звезда искажает форму плоскости, создавая в ней круглую впадину – «гравитационный колодец» со звездой на дне, и будем считать, что частицы всегда движутся по кратчайшему пути, называемому геодезической линией. Поскольку пространственно-временной континуум искривлен, кратчайшим расстоянием в нем перестает быть прямая. К примеру, частица может угодить во впадину и начать описывать круги по стенке на постоянной высоте, как планета на замкнутой орбите.

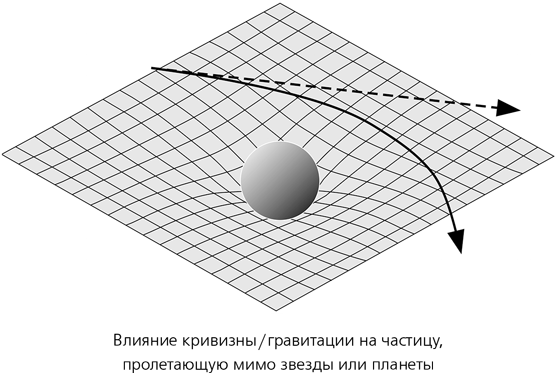
Вместо гипотетической силы, которая заставляет траекторию частицы отклоняться от прямой линии, Эйнштейн ввел пространство-время, которое уже искривлено и кривизна которого влияет на траекторию движущейся частицы. И не надо никакого дальнодействия: пространство-время искривлено потому, что именно так влияют на него звезды, а все тела, движущиеся по орбитам, реагируют на кривизну поблизости. То, что мы и Ньютон называем тяготением и представляем себе в виде силы, на самом деле является кривизной пространства-времени.

Эйнштейн записал математические формулы – уравнения поля Эйнштейна, или просто уравнения Эйнштейна[14], которые описывают, как кривизна влияет на движение масс и как распределение масс влияет на кривизну. В отсутствие какой бы то ни было массы эти формулы сводятся к специальной теории относительности. Так что все необычные эффекты, такие как замедление времени, присутствуют и в общей теории относительности. В самом деле, гравитация может вызвать замедление времени даже для неподвижного объекта. Как правило, такие парадоксальные эффекты слабы, но в крайних обстоятельствах поведение, предсказанное теорией относительности (любой из них), значительно отличается от Ньютоновой физики.

Вы думаете, что все это звучит безумно? Поначалу многие так думали. Но сегодня всякий, кто в поездках пользуется спутниковой навигацией, полагается на специальную и общую теории относительности. Расчеты, которые сообщают вам, что вы находитесь на окраине Бристоля и движетесь на юг по дороге M32, основаны на навигационных сигналах спутников на околоземных орбитах. Процессор в вашем гаджете, вычисляющий ваше положение, должен исправлять полученные со спутников данные, чтобы учесть два эффекта: скорость движения спутника и его положение в гравитационном колодце Земли[15]. Первая поправка задействует специальную теорию относительности, вторая – общую. Без них прибор спутниковой навигации всего за несколько дней забросил бы вас в середину Атлантического океана.

Общая теория относительности показывает, что Ньютонова физика не является истинной и точной «системой мира», каковой ее считал сам Ньютон (и почти все остальные ученые до XX века). Однако это открытие не означало конца Ньютоновой физики. Более того, сегодня она используется намного шире и в куда более практических целях, чем во времена Ньютона. Ньютонова физика проще, чем теория относительности, – как говорится, «сойдет для сельской местности», да и для любой другой тоже. Различия между двумя теориями становятся очевидны в основном при рассмотрении всевозможных экзотических явлений, таких как черные дыры. Астрономы и разработчики космической техники, работающие в основном на правительства или организации вроде NASA или ЕКА, до сих пор используют Ньютонову механику почти для всех расчетов. Есть, правда, несколько исключений, где время требует очень осторожного отношения. По ходу рассказа мы будем снова и снова сталкиваться с действием закона всемирного тяготения Ньютона. И не случайно: этот закон – одно из величайших научных открытий в истории человечества, его значение трудно переоценить.

Однако, когда дело доходит до космологии – исследования Вселенной в целом и в первую очередь ее происхождения, мы должны отставить Ньютонову физику в сторону. Здесь она уже не в состоянии объяснить ключевые наблюдательные результаты. Вместо нее нужно задействовать общую теорию относительности, которой умело ассистирует квантовая механика. Но даже этим двум великим теориям, судя по всему, требуется дополнительная помощь.