Характер физических законов

Рис. 7. Шаровое звездное скопление в галактике Млечного Пути

А что происходит на больших расстояниях? Эта сила действует между двумя звездами; но будет ли она действовать на расстояниях, которые не в два и не в три, а во много раз превосходят диаметр Солнечной системы? На рис. 7 показан объект, который в 100 000 раз больше, чем Солнечная система; это огромное скопление звезд. Большое белое пятно – не сплошное; оно кажется таким, потому что наши несовершенные инструменты не позволяют разглядеть в нем мелкие детали. На самом же деле оно состоит из очень-очень мелких пятнышек – обычных звезд, и вовсе не слипшихся, а сильно удаленных друг от друга, движущихся взад и вперед в этом большом шаровом скоплении.

Рис. 8. Спиральная галактика

Это одно из самых прекрасных явлений на небе – такое же прекрасное, как морские волны и закаты. Размещение материала в скоплении совершенно ясно указывает, что звезды в нем также связаны взаимным тяготением. Зная примерно расстояние до этой галактики и размещение материала в ней, мы можем приблизительно определить закон сил, действующих между звездами, – приблизительно определить, что и здесь они обратно пропорциональны квадрату расстояния. Точность этих измерений и выкладок, конечно, не может сравниться с точностью, какую мы получаем в Солнечной системе.

Рис. 9. Скопление галактик в созвездии Волосы Вероники

Тяготение действует и на еще больших расстояниях. Наше звездное скопление выглядит незаметной точкой на рис. 8, где показана типичная галактика. И опять-таки ясно, что эта галактика держится как единое целое благодаря какой-то силе. А никакой другой силы, кроме тяготения, здесь предположить нельзя. Когда мы переходим к таким масштабам, мы уже не можем проверить справедливость ньютоновского закона. Но несомненно, что в таких гигантских звездных образованиях – в этих галактиках, которые простираются на 50–100 тысяч световых лет, тогда как расстояние от Солнца до Земли составляет только 8 световых минут, – даже на таких огромных расстояниях действуют силы тяготения. Рис. 9 свидетельствует о том, что силы тяготения простираются еще дальше. Это так называемое скопление галактик. Все они собраны в один ком, как и звезды, только этот ком составлен не из звезд, а из «крошек» вроде той, которую вы видите на рис. 8.

Это чуть ли не одна сотая, а может быть, и десятая часть известной нам Вселенной, где мы имеем прямые свидетельства существования сил тяготения. Таким образом, притяжение Земли не имеет границ, хотя в газетах и пишут порой, что такое-то тело освободилось от оков земного притяжения. Притяжение становится все слабее и слабее – оно обратно пропорционально квадрату удаления от Земли: каждый раз, когда расстояние до Земли увеличивается вдвое, сила тяготения падает вчетверо и в конце концов теряется в переплетении более сильных полей тяготения других звезд. Вместе с соседними звездами Земля притягивает другие звезды, и они образуют Галактику. Галактика притягивает другие галактики, и вместе они образуют скопление – систему галактик. Таким образом, притяжение Земли нигде не кончается, но убывает медленно и строго закономерно, может быть, до самых пределов Вселенной.

Закон тяготения отличается от многих других законов. Ясно, что он играет большую роль в механике Вселенной. И покуда речь идет о Вселенной, этот закон всюду находит практическое применение. Но на Земле, как ни странно, закон тяготения дает нам гораздо меньше практически полезных сведений, чем другие законы физики. Только в этом смысле нетипичен выбранный мной пример. Кстати говоря, невозможно выбрать такой пример, который был бы типичен во всех отношениях. Это удивительное свойство нашего мира. Единственные практические приложения этого закона, которые мне приходят на ум, – это, пожалуй, некоторые методы геологической разведки, предсказание приливов и в последнее время расчет движения искусственных спутников и межпланетных станций. Да, и еще одно современное приложение: закон Ньютона позволяет заблаговременно вычислять положения планет астрологам, которые публикуют свои гороскопы в журналах. Поистине мы живем в удивительном мире: все новейшие достижения человеческой мысли используются только для того, чтобы разнообразить чепуху, существующую вот уже две тысячи лет.

Рис. 10. Газовая туманность (в созвездии Ориона)

Теперь я расскажу, где именно тяготение существенно влияет на жизнь Вселенной. Один из интересных в этом смысле примеров – образование звезд. На рис. 10 показаны газообразные туманности внутри нашей Галактики. Это не скопление звезд, это газ. Черные пятнышки – места, где газ сжался и уплотнился за счет притяжения. Процесс этот, может быть, начинается с ударных волн, но потом благодаря притяжению газ стягивается все плотнее и плотнее, и образуются большие шаровые тучи газа и пыли. По мере уплотнения они разогреваются все больше и больше, начинают светиться и превращаются в звезды.

Звезды рождаются из газа, который чересчур сжался под действием притяжения. Иногда звезды взрываются, выбрасывают пыль и газы, потом пыль и газы снова собираются и снова образуют звезды – все это похоже на вечное движение.

Как я уже сказал, тяготение действует на огромных расстояниях. Но Ньютон утверждал, что взаимно притягиваются все предметы. А правда ли, что любые два предмета притягивают друг друга? Можем ли мы сами поставить такой опыт, а не гадать, глядя на небо, притягиваются ли планеты? Такой прямой опыт сделал Кавендиш[7] при помощи прибора, который показан на рис. 11. Идея состояла в том, чтобы подвесить на очень тонкой кварцевой нити стержень с двумя шарами и затем поднести к ним сбоку два больших свинцовых шара, как показано на рисунке. Притяжение шаров слегка перекрутит нить – слегка, потому что силы притяжения между обычными предметами очень слабы. Силу притяжения между двумя шарами можно измерить. Кавендиш назвал свой опыт «взвешиванием Земли». Педантичный и осторожный преподаватель наших дней не позволит студентам так выразиться; нам пришлось бы сказать «измерение массы Земли». При помощи такого прибора Кавендишу удалось непосредственно измерить силу, расстояние и величину обеих масс и, таким образом, определить постоянную тяготения G. Вы скажете: «Взвешивание Земли представляет собой почти такую же задачу. Мы знаем силу притяжения, знаем массу объекта, который притягивается, и знаем, насколько он удален, но мы не знаем ни массы Земли, ни постоянной тяготения, а только их произведение». Измерив постоянную и зная, как Земля притягивает предметы, мы сможем вычислить ее массу.

Этот опыт впервые позволил косвенно определить, насколько тяжел, массивен шар, на котором мы живем. Результат его невольно вызывает удивление, и я думаю, что именно поэтому Кавендиш назвал свой опыт «взвешиванием Земли», а не «определением постоянной уравнения тяготения». Между прочим, он одновременно взвешивал и Солнце и все остальное, потому что притяжение Солнца определяется точно таким же способом.

Интересно было проверить закон тяготения еще с одной стороны: пропорционально ли притяжение массе. Мы знаем, что ускорение прямо пропорционально действующей силе и обратно пропорционально массе. Поэтому если сила притяжения в точности пропорциональна массе, то два тела с разной массой должны одинаково менять свою скорость в поле тяготения. Иначе говоря, два различных предмета в вакууме, независимо от их массы, за одинаковое время пролетят по направлению к Земле одинаковые расстояния. Такие опыты ставил еще Галилей на падающей башне в Пизе. Это означает, например, что какая-нибудь вещь внутри искусственного спутника Земли будет двигаться точно по такой же орбите, как сам спутник, т. е. будет парить внутри его. И все это – следствие того факта, что сила пропорциональна массе, а ускорение обратно пропорционально массе.

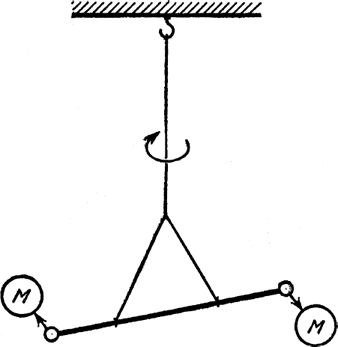
Рис. 11

Насколько точно это утверждение? На опыте его проверил Этвеш[8] в 1909 г., а впоследствии более тщательно – Дикке[9]. Теперь мы знаем с точностью до одной десятимиллиардной, что сила пропорциональна массе. Как удалось добиться такой точности? Предположим, вы хотите определить, в какой мере подчиняется этому правилу притяжение Солнца. Вы знаете, что Солнце притягивает всех нас. Оно притягивает Землю, но, предположим, вы хотите знать, в точности ли это притяжение пропорционально массе. Сначала опыт был проделан над сандаловым деревом, потом экспериментировали с медью и свинцом, а теперь пробуют на полиэтилене. Земля вращается вокруг Солнца, поэтому инерция отбрасывает земные тела от Солнца тем сильнее, чем больше инерция. Но, согласно закону тяготения, тела притягиваются к Солнцу – и тем сильнее, чем больше их масса. Поэтому если они притягиваются к Солнцу не в той же пропорции, в какой отбрасываются инерцией, то один предмет будет, например, стремиться к Солнцу, а другой – прочь от него. И тогда, прикрепив эти два предмета к коромыслу Кавендиша, мы увидим, что оно повернется по направлению к Солнцу и перекрутит кварцевую нить. На самом деле нить не перекручивается, и с той точностью, которую дает этот опыт, мы знаем, что притяжение двух предметов строго пропорционально центробежному эффекту, который обусловлен инерцией. Таким образом, сила притяжения объекта пропорциональна коэффициенту инерции, или, другими словами, массе.

Примечания