
120 детских вопросов о физике и окружающем мире
Так что мы можем сделать простой, но шокирующий вывод: у летящего камня (как и у любого тела в нашей Вселенной) нет «истинной» траектории движения. И чтобы говорить о траектории и, тем более, производить её расчёт, нужно обязательно указывать, относительно какой системы отсчёта это выполняется.
Легко ли поднять Землю рычагом?
Широко известно выражение Архимеда «Дайте мне точку опоры, и я подниму Землю!»1, которое давно стало крылатым. Однако, если разобраться в вопросе, то станет понятно – поднять Землю гипотетически можно, но на практике ни Архимед, ни кто-либо другой сделать этого не сможет.
Для начала разберёмся, почему с помощью рычага можно перемещать тяжёлые предметы. Рычаг – это простейший механизм, в котором используется закон сохранения энергии. При перемещении рычага оба его плеча, независимо от их длины, должны совершать равную работу. А работа – это произведение силы, приложенной к рычагу, на путь (или перемещение). Понятно, что короткое плечо рычага может переместиться на меньшее расстояние, чем длинное плечо, но так как работа, совершаемая плечами одинакова, то на коротком плече возникает большее усилие. При этом длинное плечо совершает больший путь с приложением меньшей силы.
Теперь понятно, о чём думал Архимед – рычагом можно поднять любую массу, даже Землю, для этого достаточно найти рычаг достаточной длины и точку опоры для него. Но вот именно здесь-то Архимед и просчитался.
Простые расчёты приводят к весьма неожиданным результатам. Чтобы человек мог «поднять» Землю хотя бы на 1 см, потребуется рычаг, длина плеч которого отличается в 1023 раз (число с 23 нулями)! Откуда такая разница? Всё просто: масса Земли составляет примерно 6х1024 кг, а человек в среднем может поднять 60 кг, то есть – разница в те самые 1023 раз. При такой длине рычага перемещение его короткого плеча на 1 см потребует перемещения длинного плеча на 1018 (число с 18 нулями) километров или чуть более 100 тысяч световых лет!
При доступной для человека скорости перемещения рычага в 1 м/с весь процесс займёт колоссальное количество времени. При указанной скорости наш Архимед за час сможет сдвинуть рычаг на 3,6 км, за год (8760 часов) – на 31536 км. А чтобы сдвинуть рычаг на 1018 км, потребуется около 31,8 триллионов лет – это примерно в 2200 раз больше текущего возраста Вселенной! Ну, а если пофантазировать и предположить, что Архимед нашёл способ двигать рычаг со скоростью света, то на всю работу потребуются те самые 100 000 лет.
Так что гипотетически сдвинуть Землю Архимед мог бы, но вы уже поняли, насколько это сложная и фантастическая по своей сути затея.
Как балансировать предметами?
Наверняка, вы не раз видели фокус с балансированием предметами: артист (который называется балансёром) держит на одном пальце трость, посуду, стул или даже своего коллегу, и удивляет публику мастерством. Однако балансирование предметами – это не так уж и сложно, как может показаться на первый взгляд. Чтобы понять это, нужно разобраться в некоторых законах механики.
Для начала давайте разберёмся, почему предметы устойчивы. Всё дело в расположении центра тяжести тела относительно его опоры. Для устойчивости должно соблюдаться простое правило: отвесная линия, проведённая из центра тяжести тела, должна проходить через площадь опоры. Как только центр тяжести оказывается вне опоры – тело опрокидывается.
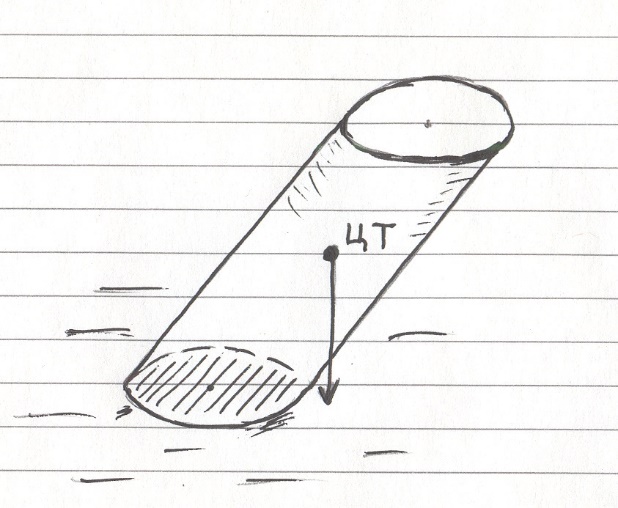
Такой цилиндр опрокинется, так как его центр тяжести (ЦТ) выходит за пределы площади опоры
Теперь посмотрим на балансёра с тростью – он постоянно балансирует ею, двигает из стороны в сторону. Зачем он это делает? А затем, чтобы постоянно удерживать центр тяжести трости над её точкой опоры! При отклонении трости её центр тяжести выходит за границы опоры – балансёр тут же подводит опору под центр тяжести, и трость не падает.
Интересно, что важную роль в этом деле играет высота центра тяжести балансируемого предмета. Если он расположен слишком низко, то при отклонении тела быстро подвести опру под центр тяжести не получится. А если центр тяжести расположен достаточно высоко, то при его отклонении гораздо проще переместить опору в нужное место. Так что не удивляйтесь, когда артист балансирует тяжёлой вещью на тонкой ножке или трости – такой трюк выполнять гораздо проще, чем балансировать короткими и круглыми предметами.
Конечно, это нисколько не умаляет труда и таланта артистов – ведь они должны не просто знать законы физики, но и уметь применять их. А это достигается годами тренировок, проб и ошибок.
Насколько тесно тела контактируют друг с другом?
Возьмите (мысленно или реально) две железных пластины, и измерьте площадь их большой стороны – пусть она будет равной 10 см2. Теперь сложите пластины вместе, и скажите – какова площадь их контакта? Ответ, вроде бы, очевиден – те самые 10 см2. Однако не торопитесь с выводами! Немного подумав, мы придём к выводу, что фактическая площадь контакта тел отличается от площади этих тел.
Чтобы понять, насколько плотно тела прижимаются друг к другу, нужно пристально посмотреть на их поверхность. Желательно через микроскоп. Мы увидим, что даже отполированные стальные бруски имеют шероховатую поверхность, изрытую микроскопических размеров горами и ущельями. Эти микронеровности практически невозможно устранить, а, к тому же, они постоянно подвержены изменениям при трении тел друг о друга – какие-то неровности выравниваются, но в другом месте появляются другие.
При соприкосновении тел в контакт входят именно эти микронеровности, причём только самые большие и высокие из них. Это снижает фактическую площадь контакта тел, причём значительно – например, наши железные бруски будут контактировать всего 1 % своей площади! То есть, при номинальной площади контакта 10 см2 фактическая площадь контакта составляет 10 мм2! У тел с большей шероховатостью площадь контакта может быть ещё меньшей.
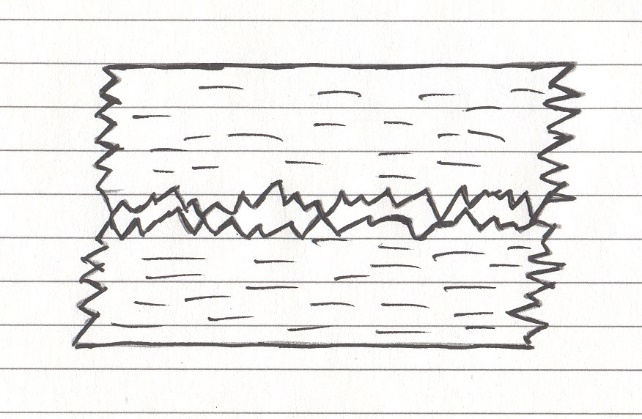
Поверхности контактирующих тел при сильном увеличении
Фактическая площадь контакта тел играет важнейшую роль в науке и технике, её приходится учитывать при расчётах многих конструкций и механизмов. В противном случае возникали бы ошибки, например, в трущихся деталях машин, а поэтому станки, двигатели или измерительные приборы работали бы неправильно.
Поэтому в следующий раз прикладывая твёрдые предметы друг к другу, помните, что они в действительности едва касаются друг друга своими микронеровностями.
Где центр тяжести летящей ракеты?
Этот вопрос на первый взгляд может показаться немного странным – конечно же, центр тяжести ракеты находится где-то в её центре. Однако призадумавшись, вы поймёте, что это не совсем так, ведь ракета постоянно теряет массу в виде истекающих из двигателей газов. А ещё немного подумав, вы и вовсе придёте к удивительному выводу, что центр тяжести летящей ракеты находится очень, очень, очень далеко за её пределами!
Что такое ракета? Её можно представить как тело, которое постоянно теряет массу – ведь топливо сгорает с образованием газов, которые истекают из сопла и создают реактивную тягу. Эти газы, а вместе с ними и часть массы ракеты, остаются где-то позади. И здесь мы должны вспомнить о существовании закона движения центра тяжести (а точнее – центра инерции системы) – движение центра инерции тела или системы тел не может быть изменено действием одних лишь внутренних сил. Что это значит? А то, что в ракете, как в замкнутой системе, положение центра тяжести не может измениться – он всегда расположен там, где и был до начала взлёта!
При этом для ракеты замкнутой системой является целая связка – сама ракета, истекающие из неё газы и, что самое удивительное, вся наша планета, о которую ударяются газы при взлёте. Получается, что центр тяжести ракеты после взлёта, даже если она летит на Луну или к другим планетам, всегда остаётся на Земле! И нужно учесть, что наша планета тоже получает некоторый импульс, сдвигаясь в противоположном от взлёта ракеты направлении. Этот сдвиг невозможно зафиксировать, так как он пренебрежительно мал, но он есть, и все законы механики сохраняются.
Так что центр тяжести (а точнее – центр инерции) любой взлетающей ракеты и всех космических аппаратов ни на мгновение не покидал Землю, а располагается где-то у центра нашей планеты.
С каким ускорением летит парашютист?
Иногда коварные учителя физики задают простой вопрос: а какое ускорение при спуске на землю имеет парашютист? Вопрос очень простой, но каверзный, а самое главное – позволяет посмотреть на ускорение в новом свете.
Итак, вот парашютист начал свой свободный полет, выпрыгнув из самолёта, и вскоре открывает парашют. Представим, что движение к земле происходит с некоторым очень малым ускорением – хотя бы 0,1 м/с2, то есть – за каждую секунду его скорость увеличивается всего на 0,1 м/с. С какой скоростью парашютист встретится с землёй, если он начал падение с высоты 1000 м и при этом имел начальную скорость 5 м/с? Даже несмотря на столь малое (казалось бы) ускорение, результат будет плачевным: парашютист в конце пути будет иметь смертельную скорость 15 м/с или 54 км/ч. А взяв высоту 5000 метров, мы в конце пути получим скорость почти 200 км/ч, что равносильно отсутствию парашюта.
Но, как мы знаем, парашютисты благополучно приземляются, выпрыгнув в любой высоты. Отсюда мы можем сделать вывод, что скорость парашютиста равномерна!
Кстати, здесь можно обратить внимание на связь ускорения, времени и пути: тело, имея даже крошечное ускорение, но обладая большим запасом времени, может приобрести колоссальную скорость. Например, космический аппарат, имея ускорение всего в 1 мм/с2 и начальную скорость в 10 км/с, за год может разогнаться до 41,5 км/с, за пять лет – до 167,7 км/с, а за десять лет – до 325,3 км/с! Примерно такого порядка ускорение обеспечивают космическим аппаратам ионные двигатели. Подобными двигателями оснащены многие современные и будущие космические аппараты, изучающие астероиды, дальние планеты и объекты пояса Койпера.
Поэтому не стоит свысока смотреть на малые ускорения – дайте им время, и они сделают большую работу! А парашютист снижается с постоянной скоростью, и только по этой причине он может без вреда для здоровья спуститься с небес на землю.
Что делает космический спутник – летит или падает?
Говоря о космических аппаратах и о космических телах вообще, мы привыкли использовать слово «полёт» – спутник летит вокруг Земли, а сама Земля летит вокруг Солнца. Однако законы небесной механики нам говорят, что космические тела скорее не летят, а падают! И вы сейчас поймёте, что это действительно так.
Начнём с самого простого: возьмите камень, влезьте на гору, и бросьте его горизонтально – камень полетит по дуге, и упадёт на землю. Вновь возьмите и бросьте камень, но теперь сильнее – камень полетит дальше, но всё равно упадёт. Так, раз за разом бросая камень со всё возрастающей силой, вы добьётесь того, что он никогда не упадёт, а примерно через полтора часа прилетит вам в спину (и он сделал бы так, не будь у нашей планеты атмосферы). Проще говоря, вы сделаете из камня искусственный спутник Земли – для этого вам пришлось разогнать камень до так называемой первой космической скорости, равной примерно 7,9 км/с.
При наблюдении за полётом камня можно заметить интересную особенность: камень всегда летит по дуге, и в первую секунду путь его под действием силы притяжения отклонится от горизонтали на 5 метров. Это происходит независимо от скорости полёта, и даже наш камень-спутник, проделывая 7,9 км в каждую секунду, отклоняется от воображаемой касательной на 5 метров. Но, в отличие от других камней, спутник не падает на Землю, а всегда оказывается на одной высоте над её поверхностью.
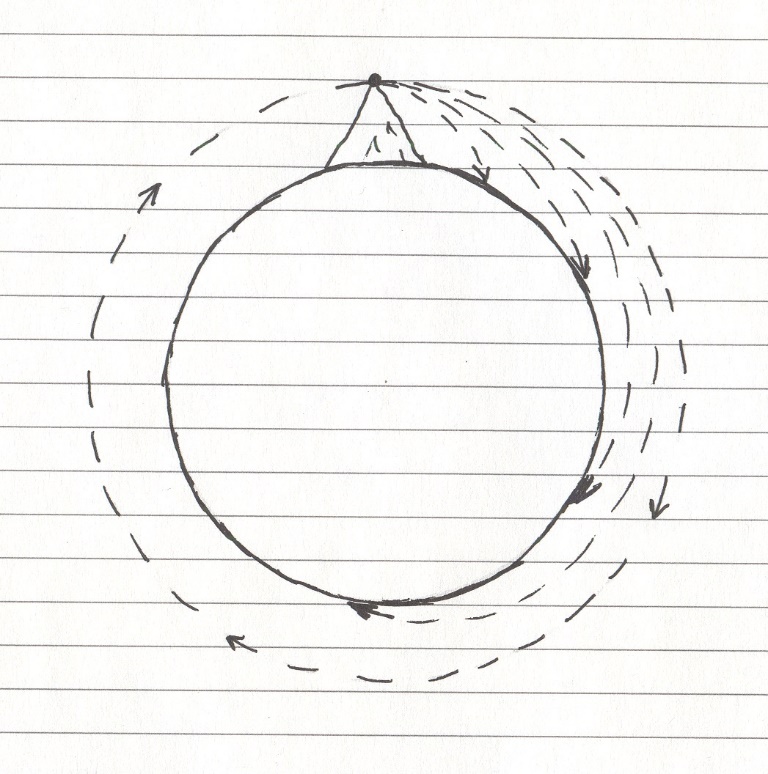
Мысленный эксперимент Ньютона – бросание тел с горы со всё возрастающей скоростью
Кстати говоря, этот мысленный эксперимент придумал ещё Исаак Ньютон, и именно ему принадлежит идея о возможности полёта тел вокруг Земли.
К чему все эти рассуждения? А к тому, что, как и другие камни, наш камень-спутник не просто летит вокруг Земли – он на неё падает! И пока его скорость не станет меньше 7,9 м/с, он не упадёт – те самые 5 метров падения по вертикали компенсируются высокой скоростью по горизонтали, и Земля постоянно как бы уходит из-под ног нашего спутника.
Так на Землю падают и не могут упасть все космические тела, в том числе и Луна. А сама Земля в своём орбитальном движении падает на Солнце, но из-за орбитальной скорости около 30 км/с остаётся почти на одинаковом расстоянии от светила. Этому закону подчиняются вообще все тела, движущиеся в поле тяготения – начиная от крошечных метеоритов, и завершая огромными галактиками, которые сталкиваются друг с другом.
Что такое баллистический маятник?
Как определить скорость пули, тягу реактивного двигателя или эффективность взрывчатки? Может показаться, что это очень сложная задача, однако в действительности всё довольно просто. Нам на помощь приходят элементарные законы физики и простейший прибор – баллистический маятник.
В самом простом случае баллистический маятник представляет собой мешок или ящик с песком, подвешенный на одном или нескольких подвесах. Как понятно из названия, маятник может раскачиваться на подвесах. Масса маятника должна быть строго известной, иначе эксперименты будут давать ошибку.
Итак, встанем на некотором расстоянии от маятника, и выстрелим в него – маятник в момент попадания пули отклонится и поднимется на некоторую высоту. Измерив эту высоту и проделав несложные вычисления, можно узнать скорость пули. Как это возможно? Благодаря закону сохранения количества движения.
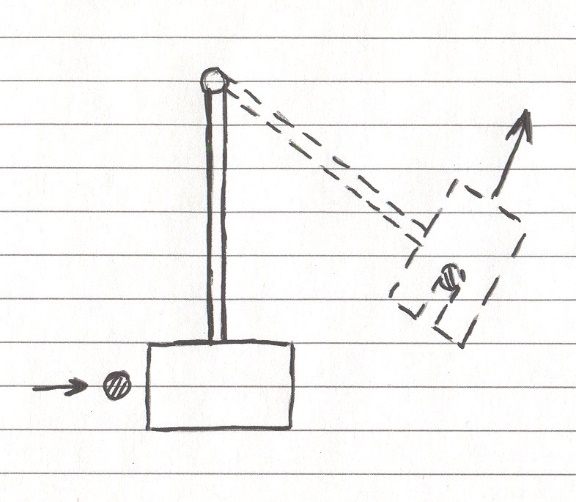
Баллистический маятник. До удара он покоится, после столкновения с движущимся снарядом – отклоняется назад
Снаряд и маятник можно считать замкнутой системой, в которой не участвуют внешние силы (сопротивлением воздуха можно пренебречь), а в любой замкнутой системе действует закон сохранения количества движения. В начале эксперимента пуля была подвижной, а маятник – неподвижным, затем пуля передала маятнику некоторый импульс, в результате чего маятник приобретает скорость и отклоняется – при всём этом общее количество движения системы осталось неизменным.
Но как высота подъёма маятника связана со скоростью пули? Всё дело в той кинетической энергии, которую приобретает маятник от пули – в наивысшей точке подъёма маятника вся его кинетическая энергия переходит в потенциальную. Измерив высоту подъёма, мы рассчитаем потенциальную энергию маятника (по формуле E=mgh, где m – масса маятника вместе с пулей, h – высота полёта, а g – ускорение свободного падения), отсюда найдём кинетическую энергию (E=mv2/2, где v – скорость движения маятника), а значит – скорость движения маятника. Наконец, закон сохранения количества движения (исходя из соотношения mv=(M+m)v1, где m – масса пули, M – масса маятника, v – скорость пули, v1 – скорость маятника после попадания пули) поможет из скорости маятника получить скорость пули.
Сегодня существует масса разновидностей баллистических маятников – они выполняются в виде небольших пушек с зарядами, в виде стендов с реактивными двигателями, и т.д. Но все они основаны на одних законах, поэтому позволяют легко измерять скорости, импульсы и многие другие физические величины различных предметов и приборов.
Как фигурист изменяет скорость своего вращения?
Наверняка, вы не раз видели, как фигуристы выполняют самые удивительные трюки – это красиво и очень интересно. Но обращали ли вы внимание на то, как фигуристы вращаются? Вот спортсмен закручивается с раскинутыми руками, затем притягивает руки к груди, и резко увеличивает скорость вращения – это они могут проделывать в полёте, в приседе, и даже в паре. Но как у фигуристов получается так раскручиваться, ведь они, кажется, даже не прилагают для этого особых усилий?
Фигуристы опираются на закон сохранения момента импульса (или закон сохранения углового момента), который сводится к следующему: каждое вращающееся тело имеет некоторое количество движения, или момент импульса, который без воздействия внешних сил со временем остаётся неизменным. Для вращающегося тела также присуща ещё одна величина – момент инерции, который зависит от массы и конфигурации тела. Например, большой маховик обладает высоким моментом инерции, так как вращающаяся масса находится на некотором расстоянии от центра вращения – такой маховик трудно раскрутить и не менее трудно остановить. А стержень такой же массы имеет гораздо меньший момент инерции, так как вся вращающаяся масса сосредоточена у оси вращения.
Наконец, мы подошли к самому главному: момент импульса вращающегося тела находится в простой зависимости от угловой скорости и от момента инерции: L = Iω (где L – момент импульса, I – момент инерции, ω – угловая скорость). Теперь становится понятным, что если тело раскрутить и уменьшить его протяжённость, то оно вследствие уменьшения момента инерции станет вращаться быстрее, и наоборот.
В этом и заключается секрет фигуристов. Раскручиваясь, спортсмен приобретает некоторый момент импульса. Притянув руки к груди, фигурист уменьшает момент инерции, и вследствие закона сохранения момента импульса его скорость вращения возрастает. Для остановки вращения фигурист сначала разводит руки в стороны (увеличивает момент инерции), а затем гасит оставшуюся скорость трением коньков об лёд.
Закон сохранения момента импульса является одним из фундаментальных законов сохранения в природе, и играет важную роль во Вселенной. Например, при взрывах Сверхновых звёзд возникают нейтронные звезды или чёрные дыры, которые имеют огромную скорость вращения – до нескольких тысяч оборотов в секунду! Это вращение возникает вследствие описанных выше эффектов: Сверхновыми взрываются массивные (в 8 – 10 раз тяжелее Солнца) и большие (диаметром в миллионы километров) звезды, имеющие невысокую скорость вращения. В момент взрыва светило сбрасывает с себя внешнюю оболочку, а на его месте остаётся тяжёлая нейтронная звезда (или даже чёрная дыра) диаметром в лучшем случае километров 30. Такое катастрофическое уменьшение момента инерции и приводит к колоссальному увеличению скорости вращения. Конечно, это только один из примеров действия закона, но он очень показателен.
Так что в следующий раз помните, какие важные законы стоят за красотой элементов фигурного катания.
Почему тормозит автомобиль?
При необходимости остановить автомобиль водитель жмёт на педаль тормоза, и машина замедляет своё движение. А вы задавались когда-нибудь вопросом: почему вообще работают тормоза? Если разобраться в этом, то ответ может показаться несколько неожиданным.
Движущаяся машина имеет некоторую кинетическую энергию, и чем выше скорость, тем выше энергия. Для остановки следует уменьшить количество кинетической энергии – как это сделать? Самое простое – поставить перед движущимся телом препятствие, при ударе о которое вся кинетическая энергия перейдёт… А во что она перейдёт? По большей части – в тепло. Тело и препятствие в результате столкновения нагреются, а некоторая часть энергии перейдёт в деформации. Можно использовать и более щадящий способ: перед движущимся телом поместить поверхность с высоким коэффициентом трения или просто песок. В этом случае вся энергия за счёт сил трения тоже перейдёт в тепло и деформации.
Для транспорта эти способы не годятся, хотя последний из них представляет определённый интерес, но в изменённом виде – нужно поверхность с высоким коэффициентом трения возить с собой. Например, на колёса поставить подвижные и неподвижные детали, которые в нужный момент приводились бы в соприкосновение и испытывали трение. Именно так и устроены фрикционные тормоза – есть диски или барабаны, вращающиеся вместе с колёсами, и неподвижные тормозные колодки, которые в момент остановки плотно прижимаются к дискам.
Таким образом, автомобили, поезда и другие колёсные транспортные средства тормозят потому, что их кинетическая энергия с помощью силы трения переводится в тепло, которое просто-напросто рассеивается. Заметим, что автомобили обладают большой кинетической энергией, поэтому детали тормозов испытывают большой нагрев – нередко они раскаляются докрасна!
НЕОЧЕВИДНОЕ В ОЧЕВИДНОМ
Существуют вопросы, ответы на которые кажутся нам очевидными и само собой разумеющимися. Но стоит копнуть поглубже, как всё встаёт с ног на голову, и в очевидном обнаруживается неочевидное.
Сколько весит килограмм?
Что за странный вопрос? Ведь килограмм – он и есть килограмм! Но не спешите с выводами, ведь здесь мы путаем два хотя и связанных, но разных понятия – вес и массу.
Если говорить просто, то масса – это величина, определяющая количество материи в теле или меру его инертности. Масса является фундаментальной величиной, она присуща всем телам во Вселенной и почти всем частицам – массы лишены только фотоны, которые из-за этого всегда движутся со скоростью света.
Другое дело – вес. Это сила, с которой тело действует на опору или подвес. И самое интересное, что вес одного тела, оказавшегося в разных условиях, может изменяться от нуля до невообразимых величин (но не до бесконечности!). Мы всегда имеем дело с весом, возникающим в поле силы тяжести нашей родной планеты. Но и в обыденной жизни мы постоянно сталкиваемся с изменениями веса, хотя и с краткосрочными: при ускорении и торможении автомобиля, при начале движения лифта вверх и вниз, на каруселях и даже просто в прыжке.
Избавиться от массы невозможно, а лишиться веса – легко. Даже если вы просто подпрыгните, то на краткий миг не будете весить ровным счётом ничего! Ведь в этот момент вы не действуете на опору, а значит – нет силы, нет и веса. Ещё дольше этот эффект можно наблюдать при прыжке с парашютом. Но полная невесомость достигается в космических кораблях. И вы не раз видели кадры парящих космонавтов и необычное поведение предметов внутри космического корабля.
Однако в невесомости теряется только вес, но не масса. И именно в этих условиях масса полностью проявляет себя как мера инертности тел. Например, космонавту приходится прилагать немало усилий, чтобы сдвинуть с места тяжёлый предмет. Но как только этот предмет будет сдвинут – он по инерции продолжит движение, что и облегчает работы по переноске грузов из транспортного космического корабля на космическую станцию и наоборот.
Это «работает» и в обратную сторону: вес тела даже в обычных условиях может очень сильно увеличиваться. Например, в момент удара по мячу его вес и вес ноги на короткое мгновение может увеличиваться по меньшей мере в 20 – 30 раз. А снаряд в момент выстрела из орудия становится тяжелее в 30 000 – 40 000 раз.
Наконец, масса и вес измеряются в разных единицах. Масса – в привычных килограммах (кг), а вес – в ньютонах (Н). В условиях Земли вес в 1 ньютон имеет тело массой примерно 102 грамма. На Луне это значение в 6 раз меньше, на астероидах – в сотни и тысячи раз меньше, на Юпитере – в 2,5 раза больше, на Солнце – в 27,85 раз больше, а на нейтронной звезде – в 100 – 200 миллиардов раз больше.
И может показаться, что самый большой вес тела должны иметь у чёрных дыр – объектов, притяжение которых настолько велико, что даже свет не может вырваться из них. Но нет! У чёрной дыры нет поверхности, и ничто не может вырваться из неё, поэтому и о весе тел, оказавшихся рядом с ней, говорить в принципе невозможно.
Так что не везде во Вселенной килограмм весит одинаково!
Вечный вопрос: что тяжелее – тонна дерева или тонна железа?
Часто можно услышать вопрос: что тяжелее – тонна железа или тонна дерева? Иногда вместо дерева вес железа сравнивают с пухом, но суть от этого не меняется. Нередко люди отвечают, что тонна железа тяжелее, кто-то склонен считать, что железо и дерево весят одинаково, а кто-то делает выбор в пользу дерева. Однако здесь не всё так однозначно, и ответ зависит от того, с какой стороны посмотреть на эту задачку.
Для начала рассмотрим, что представляет собой тонна дерева и тонна железа. Плотность железа составляет почти 7,9 г/см3, плотность древесины зависит от породы, для примера возьмём нашу русскую берёзку с плотностью около 0,65 г/см3. Поэтому тонна дерева занимает примерно в 12 раз больший объем, чем тонна железа. Это имеет важные последствия.