Электроника и электротехника. Шпаргалка

10. МЕТОД НАЛОЖЕНИЯ

Метод наложения основан на том, что в линейных электрических цепях ток любой ветви может быть определен как алгебраическая сумма токов от каждого источника в отдельности.

Расчет электрических цепей методом наложения производят в таком порядке. Из электрической цепи удаляют все источники ЭДС и напряжения, кроме одного. Сохранив в электрической цепи все резистивные элементы, в том числе и внутренние сопротивления источников, производят расчет электрической цепи. Внутренние сопротивления источников с указанными напряжениями полагают равными нулю.

Подобным образом поступают столько раз, сколько имеется в цепи источников.

Результирующий ток каждой ветви определяют как алгебраическую сумму токов от всех источников.

Для того чтобы результирующие токи совпадали с действительными направлениями, целесообразно выбирать положительные направления результирующих токов после определения токов от всех источников.

Метод наложения весьма удобен для анализа явлений, происходящих в электрических цепях при изменении их параметров.

Например, используя метод наложения, нетрудно определить характер изменения токов ветвей в цепи (см. рис. 13) при увеличении ЭДС E1 до E1′ .

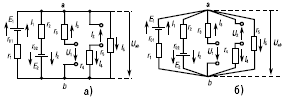
Рис. 13. Схема электрической цепи

Действительно, предположим, что при некоторых параметрах цепи до увеличения E1 установились токи, действительные направления которых совпадают с указанными на рисунке 13. Для решения задачи заменим мысленно увеличение ЭДС E1 введением в первую ветвь дополнительного источника с r0доп = 0 и Едоп = E1′ – E1. После этого удалим из цепи все источники, кроме источника с ЭДС Едоп, и определим действительные направления дополнительных токов от этого источника, которые очевидны.

Поскольку дополнительный ток первой ветви I1доп будет совпадать по направлению с током I1, для определения результирующего тока первой ветви следует воспользоваться формулой I1′ = I1 + I1доп. На основании данной формулы можно сделать вывод о том, что при увеличении Е1 ток I1 будет возрастать.

К такому же выводу можно прийти и в отношении токов других ветвей, кроме третьей.

Так как дополнительный ток третьей ветви I3доп направлен против тока I3, то для определения результирующего тока нужно использовать формулу I3′ = I3 + I3доп. В отношении результирующего тока третьей ветви можно сделать такой вывод: при увеличении ЭДС Е1 ток I3 будет сначала уменьшаться, при некотором значении Е1 окажется равным нулю, а при дальнейшем увеличении Е1 изменит направление (I3 < 0) и по абсолютному значению будет возрастать.

11. МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА

Метод эквивалентного генератора дает возможность упростить анализ и расчет электрических цепей в том случае, когда требуется определить ток, напряжение или мощность лишь одной ветви.

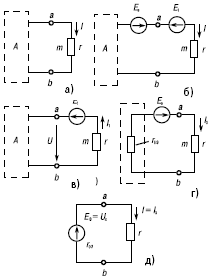
Рис. 14. Схема электрической цепи эквивалентного генератора

Предположим, что требуется найти ток I ветви amb некоторой электрической цепи (рис. 14а), остальные элементы которой сосредоточены в предела прямоугольника, представляющего собой активный двухполюсник А.

Согласно методу наложения ток I не изменится, если в данную ветвь ввести два источника, ЭДС которых Е1 и ЕЭ равны и направлены в разные стороны (рис. 14б).

Ток I можно определить как разность двух токов: I = IЭ + I1,

где I1 – ток, вызванный всеми источниками двухполюсника А и ЭДС Е1 (рис. 14в);

IЭ – ток, вызванный только ЭДС ЕЭ (рис. 14г).

Если выбрать ЭДС Е1 таким образом, чтобы получить I1 = 0, то ток I будет равен:

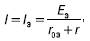
где r0Э – эквивалентное сопротивление двухполюсника А относительно выводов а и b.

Так как при I1 = 0 (рис. 14в) активный двухполюсник А будет работать относительно ветви amb в режиме холостого хода, то между выводами a и b установится напряжение холостого хода U = Ux и по второму закону Кирхгофа получим E1 = I1r + Ux. Но по условию ЕЭ = Е1, поэтому и ЕЭ = Ux. Учитывая это, формулу для определения тока I можно записать в такой форме:

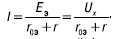
В соответствии с последней формулой электрическая цепь (рис. 14а) может быть заменена эквивалентной цепью (рис. 14д), в которой ЕЭ = Ux и r0Э следует рассматривать как ЭДС и внутреннее сопротивление некоторого эквивалентного генератора.

В результате возможности такой замены и возникло название изложенного метода.

Значения ЕЭ = Ux и r0Э можно определить как расчетным, так и экспериментальным путем. Для расчетного определения Ux и r0Э необходимо знать параметры элементов активного двухполюсника А и схему их соединения. При определении сопротивления r0Э необходимо удалить из схемы двухполюсника все источники, сохранив все резистивные элементы, в том числе и внутренние сопротивления источников ЭДС. Внутренние сопротивления источников с указанными напряжениями следует принять равными нулю.

12. ПОЛУЧЕНИЕ СИНУСОИДАЛЬНОЙ ЭДС. ОСНОВНЫЕ СООТНОШЕНИЯ

Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются во времени по синусоидальному закону, называются цепями синусоидального тока. Иногда их называют просто цепями переменного тока.

Электрические цепи, в которых значения и направления ЭДС, напряжения и тока периодически изменяются во времени по законам, отличным от синусоидального, называются цепями несинусоидального тока.

Генераторы электрических станций переменного тока устроены так, что возникающая в их обмотках ЭДС изменяется по синусоидальному закону. Синусоидальная ЭДС в линейных цепях, где содержатся резистивные, индуктивные и емкостные элементы, возбуждает ток, изменяющийся по закону синуса.

Возникающие при этом ЭДС самоиндукции в катушках и напряжения на конденсаторах, как это вытекает из выражений:

также изменяются по синусоидальному закону, так как производная синусоидальной функции есть функция синусоидальная. Напряжение на резистивном элементе будет так-же изменяться по синусоидальному закону: u = ir.

Целесообразность технического использования синусоидального тока обусловлена тем, что КПД генераторов, двигателей, трансформаторов и линий электропередачи при синусоидальной форме ЭДС, напряжения и тока получается наивысшим по сравнению с несинусоидальным током. Кроме того, при иных формах изменения тока из(за ЭДС самоиндукции могут возникать значительные перенапряжения на отдельных участках цепи.

Важную роль играет и тот факт, что расчет цепей, где ЭДС, напряжение и ток изменяются синусоидально, значительно проще, чем расчет цепей, где указанные величины изменяются по несинусоидальному закону.

Рассмотрим механизм возникновения и основные соотношения, характерные для синусоидальной ЭДС.

Для этого удобно использовать простейшую модель – рамку, вращающуюся с постоянной угловой скоростью в равномерном магнитном поле. Проводники рамки, перемещаясь в магнитном поле, пересекают его, и в них на основании закона электромагнитной индукции наводится ЭДС. Значение ЭДС пропорционально магнитной индукции B, длине проводника l и скорости перемещения проводника относительно поля υt : е = Blυt.

Выразив скорость υt через окружающую скорость υ и угол α, получим: е = Blυ sin α = Em sin α.

Угол α равен произведению угловой скорости рамки ω на время t: α = ωt.

Таким образом, ЭДС, возникающая в рамке, будет равна: е = Em sin α = Em sin ωt.

За один поворот рамки происходит полный цикл изменения ЭДС.

Если при t = 0 ЭДС е не равна нулю, то выражение ЭДС записывается в виде:е = Em sin (ωt + y),

где e – мгновенное значение ЭДС (значение ЭДС в момент времени t);

Em – амплитудное значение ЭДС (значение ЭДС в момент времени );

(ωt + ψ) – фаза;

ψ – начальная фаза.

Фаза определяет значение ЭДС в момент времени t, начальная фаза – при t = 0.

Время одного цикла называется периодом T, а число периодов в секунду – частотой f:

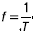
Единицей измерения частоты является c–1, или герц (Гц). Величина

в электротехнике называется угловой частотой и измеряется в рад/с.

Частота вращения рамки n и частота ЭДС f связаны между собой соотношением:

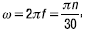
 откуда

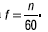
13. ЦЕПЬ, СОДЕРЖАЩАЯ КАТУШКУ С АКТИВНЫМ СОПРОТИВЛЕНИЕМ R И ИНДУКТИВНОСТЬЮ L

Реальная катушка любого электротехнического устройства обладает определенным активным сопротивлением r и индуктивностью L. Участок цепи с индуктивностью L будем рассматривать как участок, обладающий индуктивным сопротивлением xl. Уравнение напряжений, составленное по второму закону Кирхгофа для цепи с r и L, имеет вид:Ū = Ūr + Ūl.

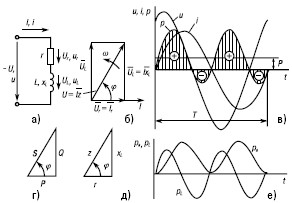
Рис. 15. Цепь, содержащая катушку с активным сопротивлением R и индуктивностью

На векторной диаграмме (рис. 15б) вектор Ur совпадает с вектором тока, а вектор Ul опережает вектор тока на 90°.

Из диаграммы следует, что вектор напряжения сети равен геометрической сумме векторов  Urи Ul. Ū = ŪR + ŪL, а его значение

Выразив напряжения через ток и сопротивления, получим

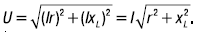
Последнее выражение представляет собой закон Ома цепи (рис. 15г):

 где z – полное сопротивление цепи.

Из векторной диаграммы следует, что напряжение цепи опережает по фазе ток на угол р и его мгновенное значение равно: υ = Um sin (ωt + φ).

Графики мгновенных значений напряжения и тока цепи изображены на рисунке 15в.

Угол сдвига по фазе φ между напряжением и вызванным им током определяют из соотношения:

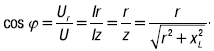
График pa(t) показывает, что активная мощность непрерывно поступает из сети и выделяется в активном сопротивлении в виде теплоты. Она равна:

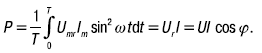
Мгновенная мощность, обусловленная энергией магнитного поля индуктивности, циркулирует между сетью и катушкой. Ее среднее значение за период равно нулю:

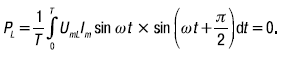
14. ЦЕПЬ, СОДЕРЖАЩАЯ РЕЗИСТИВНЫЙ И ЕМКОСТНОЙ ЭЛЕМЕНТЫ

Участок цепи с емкостью С будем представлять как участок, обладающий емкостным сопротивлением xc.

В этом случае уравнение напряжений цепи (рис. 16а) имеет вид: Ū = Ūr + Ūc

На (рис. 16б) изображена векторная диаграмма цепи r и С.

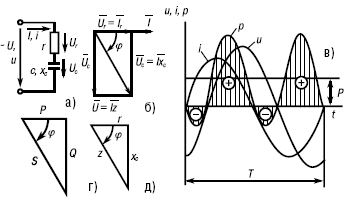
Рис. 16. Электрическая цепь, содержащая резистивный r и емкостный С элементы (а), ее векторная диаграмма (б), графики мгновенных значений (в), треугольники мощностей и сопротивлений (г и д)

Вектор напряжения Ūr совпадает с вектором тока, вектор Ūc отстает от вектора тока на угол 90°. Из диаграммы следует, что модуль напряжения, приложенного к цепи, равен:

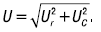
Выразив Ur и Uc через ток и сопротивления, получим:

откуда

Последнее выражение представляет собой закон Ома цепи r и C:

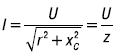
 где z – полное сопротивление.

Графики u(i), i(t) изображены на рисунке 16в. Разделив стороны треугольника напряжений (рис. 16б) на ток, получим треугольник сопротивлений (рис. 16д), из которого можно определить косинус угла сдвига фаз между током и напряжением:

Мгновенная мощность цепи:p = ui = ImsinωtUm × sin (ωt +φ)

Средняя мощность за период:

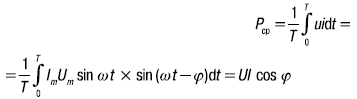
Подставив вместо cos φ его значение, получим Pср = UI cosφ = UI(r/z) = i2r = P

Таким образом, среднее значение мощности цепи с r, С, так же как и цепи с r, L, представляет собой активную мощность, которая выделяется в активном сопротивлении r в виде теплоты.

На (рис. 16в) изображен график мгновенной мощности цепи с r, С.

Энергетические процессы цепи с r, С можно рассматривать как совокупность процессов, происходящих отдельно в цепи с r и С. Из сети непрерывно поступает активная мощность. Реактивная мощность, обусловленная электрическим полем емкости, непрерывно циркулирует между источником и цепью. Ее среднее значение за период равно нулю.

15. ПОСЛЕДОВАТЕЛЬНОЕ СОЕДИНЕНИЕ R, L, C

Уравнение напряжений для цепи (рис. 17а) имеет вид: Ū = Ūr + Ūl+ Ūc

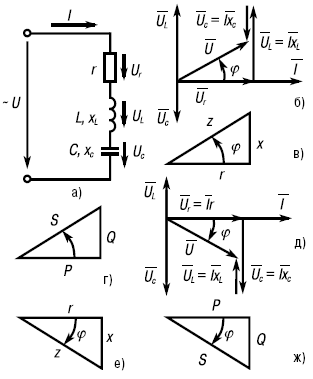
Рис. 17. Электрическая цепь, содержащая последовательно включенные r, L и С (а), ее векторная диаграмма (б), треугольники сопротивлений и мощностей (в и г) цепи при xL > xC, векторная диаграмма (д), треугольники сопротивлений и мощностей (е и ж) цепи при xC > xL.

Векторные диаграммы для цепи (рис. 17а) изображены на рисунках 17б и 17в. Вектор напряжения на активном сопротивлении совпадает с вектором тока, вектор напряжения на индуктивности Ūl опережает вектор тока на 90°, вектор напряжения на емкости Ūc отстает от вектора тока на 90°. Следовательно, между векторами напряжения на индуктивности и емкости образуется угол в 180°.

Если xL > xC, то и UL > Ūc и векторная диаграмма будет такой (см. рис. 17б), а треугольник сопротивлений – на рисунке 17в, где x = xL – xC. Если xC > xL, то UC > UL и векторная диаграмма будет иметь вид, изображенный на рисунке 17е, где x = xC – xL.

Значение напряжения, приложенного к цепи:

Выразив напряжение через ток и сопротивления, получим

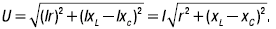
Последнее выражение представляет собой закон Ома для последовательной цепи r, L, C:

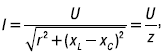
где z – полное сопротивление цепи;

x – реактивное сопротивление цепи.

На основании проведенного анализа цепи, состоящей из последовательно соединенных r, L, C, можно сделать следующие выводы.

Если xL > xC, то напряжение сети опережает по фазе ток на угол φ: υ = Um sin (ωt + φ).

Цепь имеет активно(индуктивный характер.

Если xC > xL, то напряжение сети отстает по фазе от тока на угол φ: υ = Um sin (ωt + φ).

Цепь имеет активно(емкостный характер.

16. АКТИВНАЯ, РЕАКТИВНАЯ И ПОЛНАЯ МОЩНОСТИ ЦЕПИ

Активная мощность цепи – P = UrI = I2r, Вт.

Реактивная индуктивная мощность цели, обусловленная энергией магнитного поля, – QL = ULI = I2xL, ВАР.

Реактивная емкостная мощность цепи, обусловленная энергией электрического поля, – QC = UCI = I2xC, ВАР.

Реактивная мощность цепи Q = QL – QC = I2x, ВАР,– это та мощность, которой приемник обменивается с сетью. Полная мощность цепи – S – UI = I2z, ВА, cos φ = коэффициент мощности цепи. Тогда P = S cos  φ = UI cos  φ; Q = S sin  φ = UI sin  φ;

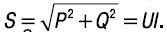
За единицу активной мощности принят ватт (Вт), реактивной мощности – вольт-ампер реактивный (ВАР), полной мощности – вольт-ампер(ВА).

Реактивные (индуктивная, емкостная) мощности, обусловленные соответственно энергией магнитного поля индуктивности и электрического поля емкости, не совершают никакой полезной работы, но они оказывают существенное влияние на режим работы электрической цепи. Циркулируя по проводам трансформаторов, генераторов, двигателей, линий передач, они нагревают их. Поэтому расчет проводов и других элементов устройств переменного тока производят исходя из полной мощности, которая учитывает активную и реактивную мощности.

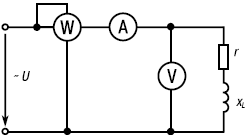
Рис. 18. Схема включения приборов дм измерении активной, реактивной и полной мощностей цепи, a также  ее параметров

Коэффициент мощности имеет большое практическое значение: он показывает, какая часть полной мощности является активной мощностью. Полная мощность и коэффициент мощности наряду с другими параметрами являются расчетными величинами и в конечном счете определяют габаритные размеры трансформаторов, генераторов, двигателей и других электротехнических устройств.

Измерение активной, реактивной, полной мощностей и cos φ, а также параметров цепи, например r и L, можно произвести с помощью ваттметра, амперметра и вольтметра, включенных в цепь по схеме, изображенной на рисунке 18.

Ваттметр измеряет активную мощность Р цепи. Полная мощность цепи равна произведению показаний вольтметра и амперметра.

Реактивную (индуктивную) мощность и коэффициент мощности цепи (рис. 18) определяют расчетным путем по формулам:

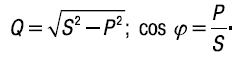
Активное сопротивление находят из формулы:

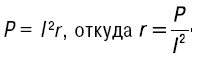
Полное сопротивление цепи -

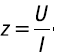
Индуктивное сопротивление -

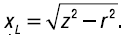
Индуктивность L определяют из формулы: xL = 2pL,

откуда

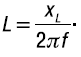
17. РЕЗОНАНС НАПРЯЖЕНИЙ

Известно, что в механической системе резонанс наступает при равенстве собственной частоты колебаний системы и частоты колебаний возмущающей силы, действующей на систему. Колебания механической системы, например колебания маятника, сопровождаются периодическим переходом кинетической энергии в потенциальную и наоборот. При резонансе механической системы малые возмущающие силы могут вызывать большие колебания системы, например большую амплитуду колебаний маятника.

В цепях переменного тока, где есть индуктивность и емкость, могут возникнуть явления резонанса, которые аналогичны явлению резонанса в механи(

ческой системе. Полная аналогия – равенство собственной частоты колебаний электрического контура частоте возмущающей силы (частоте напряжения сети) – возможна не во всех случаях.

В общем случае под резонансом электрической цепи понимают такое состояние цепи, когда ток и напряжение совпадают по фазе, и, следовательно, эквивалентная схема цепи имеет место при определенном соотношении ее параметров r, L, C, когда резонансная частота цепи равна частоте приложенного к ней напряжения.

Резонанс в электрической цепи сопровождается периодическим переходом энергии электрического поля емкости в энергию магнитного поля и наоборот.

При резонансе в электрической цепи малые напряжения, приложенные к цепи, могут вызвать значительные токи и напряжения на отдельных участках. В цепи, где r, L, C соединены последовательно, может возникнуть резонанс напряжений, а в цепи, где r, L, C соединены параллельно, – резонанс токов.

Рассмотрим явление резонанса напряжений на примере цепи (рис. 19).

Как отмечалось, при резонансе ток и напряжение совпадают по фазе, т. е. угол φ = 0, и полное сопротивление цепи равно ее активному сопротивлению:

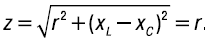
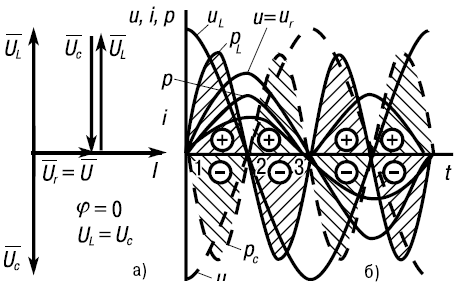
Рис. 19. Явление резонанса напряжений

Это равенство будет иметь место, если xL = xC, т. е. реактивное сопротивление цепи равно нулю: x = xL – xC.

Выразив xL и xC соответственно через L, C и f,

получим:

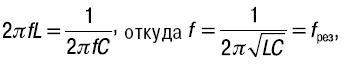
где f – частота напряжения, подведенного к контуру;

fрез – резонансная частота.

Таким образом, при xL = xC в цепи возникает резонанс напряжений, так как резонансная частота равна частоте напряжения, подведенного к цепи.

Из выражения закона Ома для последовательной цепи:

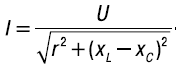
При резонансе:

IxL = IxC = UL = UC; Ur = Ir = U;

Q = QL – QC = ULI – UCI = 0.

18. РЕЗОНАНС ТОКОВ

Резонанс токов может возникнуть в параллельной цепи (см. рис. 20а), одна из ветвей которой содержит L и r, а другая – C и r.

Рис. 20. Резонанс токов в параллельной цепи

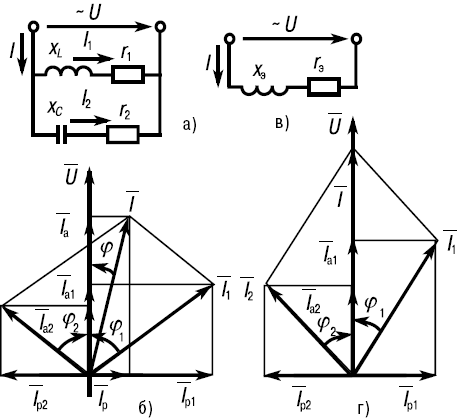
Резонансом токов называется такое состояние цепи, когда общий ток совпадает по фазе с напряжением, реактивная мощность равна нулю и цепь потребляет только активную мощность. На рисунке 20г изображена векторная диаграмма цепи (рис. 20а) при резонансе токов.

Как видно из векторной диаграммы, общий ток цепи совпадает по фазе с напряжением, если реактивные составляющие токов ветвей с индуктивностью и емкостью равны по модулю: I1p = I2p.

Общий реактивный ток цепи, равный разности реактивных токов ветвей, в этом случае равен нулю: I1p – I2p = 0.

Общий ток цепи имеет только активную составляющую, равную сумме активных составляющих токов ветвей: Ia = I1a = I2a.

В идеальном случае, когда

При резонансе токов коэффициент мощности равен единице: cos φ = 1.