
Со спичками не шутят
Используя спички, как палочки, можно изображать не только цифры и буквы. Спички имеют стандартную длину, и это свойство позволяет строить из них различные геометрические фигуры. Более того, с помощью спичек можно вести преподавание геометрии в определенных пределах программы, но только при индивидуальном обучении, потому что они маленькие и в большом классе на доске их не рассмотришь. Одна спичка – это модель отрезка. Две спички, соединенные своими серными головками, – модель угла. Из трех спичек можно выложить ломаную линию, а если её замкнуть, получится равносторонний треугольник.

Спичками можно изобразить прямой и развёрнутый, острый и тупой углы и т.д. Из четырех спичек складываются две фигуры: квадрат и ромб, различающиеся тем, что у квадрата равны не только стороны, но и все углы, а у ромба смежные углы не равны.

Плоские геометрические фигуры, у которых равны все стороны и равны все углы, называются правильными.
Из пяти спичек можно построить как правильный пятиугольник, так и неправильный, то есть с неравными углами.

Наверное, было бы интересно написать учебник геометрии, в котором все определения, все теоремы демонстрируются и доказываются на спичках, но у данной книги другое направление – это сборник занимательных задач для читателя, подготовленного хотя бы на уровне «троечника» средней школы.
Геометрические задачи распределены по характеру самих заданий на несколько разделов, а внутри раздела упорядочены по количеству требуемых в условии спичек.
Раздел А. Требуется изобразить спичками некоторую геометрическую конфигурацию или же переложить (убрать) несколько спичек в заданной фигуре так, чтобы получить определенную новую фигуру.
2-1. Как образовать треугольник одной спичкой, не ломая и не расщепляя её?
Примечание: не все задания серьёзные, могут быть и шутки, но с долей здравого смысла. Особо выделять их не будем, но предупредить должны.
2-2. При помощи двух спичек, не ломая и не расщепляя их, попробуйте образовать квадрат?
2-3. Как двумя спичками, не кладя одну поперек другой, изобразить крест?
2-4. Попросите товарища положить на стол одну спичку горизонтально. Он положит её, разумеется, так:

Затем попросите его положить возле первой спички вторую спичку вертикально. Из 100 человек 99 сделают это примерно так:
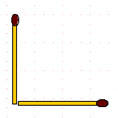
делая ошибку, ведь вторая спичка расположена тоже горизонтально. Вертикально её нужно поставить к плоскости стола.
2-5. Три спички лежат на столе. Как удалить среднюю спичку из середины, не трогая её?

2-6. Четыре спички расположены как на рисунке. Передвиньте одну из них так, чтобы получился квадрат.
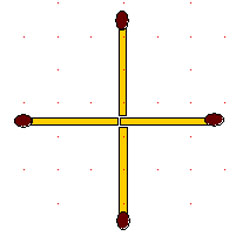
2-7. Возьмите 4 спички и расположите их таким образом, чтобы они образовали четыре прямых угла. (Кроме конфигурации из предыдущей задачи.) Когда это сделано, переложите одну спичку так, чтобы при новом расположении спички ограничивали квадрат. Сколько различных первоначальных положений четырех спичек возможно в этой задаче?
2-8. Ответьте быстро: сколько концов у 4 спичек, у 5 спичек, у пяти с половиной спичек?
2-9. Расположите 6 спичек так, чтобы каждая соприкасалась не менее чем с четырьмя другими.
2-10. Из 6 спичек постройте 6 прямоугольников и 3 квадрата.
2-11. Составьте из 6 спичек шестиугольник с четырьмя острыми углами.
2-12. Положите 6 спичек так, чтобы образовался квадрат.
2-13. Возьмите 6 спичек. Сломайте две из них пополам. Из полученных четырёх целых спичек и четырёх половинок сложите 3 равных квадрата.
2-14. В коробке было 12 спичек, из них можно построить 4 равносторонних треугольника с длиной стороны в одну спичку. Через день осталось в коробке 10 спичек, но из них снова удалось построить 4 равносторонних треугольника. Еще через день (видимо у курящего человека) осталось в коробке 9 спичек, но из них снова удалось построить 4 равносторонних треугольника. Ещё через день спичек осталось всего 6, но и их достаточно, чтобы построить 4 равносторонних треугольника. Проделайте эти выкладки.
2-15. Можно ли расположить 6 спичек так, чтобы каждая из них соприкасалась с пятью остальными?
2-16. Передвинув 2 спички и добавив ещё одну, получите из правильного шестиугольника два ромба.

2-17. Расположите 2 спички рядом так, чтобы они составляли одну прямую линию, и докажите при помощи рассуждений и дополнительного построения на спичках, правильность вашего построения.
2-18. Шесть спичек можно положить так, чтобы каждая из них касалась ровно трёх других.
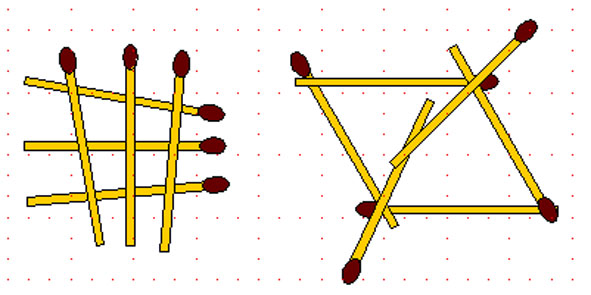
На рисунке показаны два возможных расположения. А можно ли расположить на столе 8 спичек так, чтобы каждая из них касалась ровно трёх других? Тот же вопрос для 7 спичек.
2-19. Восемь спичек положите так, чтобы образовались: один восьмиугольник, два квадрата и восемь треугольников – все в одной фигуре.
2-20. Фигура, изображенная на рисунке, составлена из 8 спичек, наложенных друг на друга. Снимите 2 спички так, чтобы осталось три квадрата.
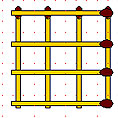
2-21. Правильный шестиугольник составлен из 6 спичек (см. рис. к задаче 2-16). Можете ли вы, добавив 3 спички, изобразить с помощью 9 полученных спичек другую правильную фигуру с шестью сторонами?
2-22. Скрепляя концы 3 спичек шариками из пластилина, легко составить один равносторонний треугольник. Возьмите 9 спичек и, так же скрепляя их концы пластилином, составьте 7 равносторонних треугольников.

2-23. Девять спичек лежат на столе, как указано на рисунке. Если взять из обоих рядов по 1 спичке, то что нужно сделать, чтобы в каждом ряду снова оказалось по 5 спичек?
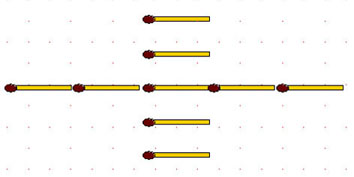
2.24. Составьте из 9 спичек три равных квадрата.
2-25. Из 9 спичек составьте 6 квадратов (допускается наложение одной спички поперёк другой).
2-26. Из 18 спичек можно сложить 2 равносторонних треугольника и 3 квадрата. А попробуйте обойтись всего девятью спичками для их построения.
2-27. Из 10 спичек сложите 3 квадрата. Затем отнимите 1 спичку и сделайте из оставшихся спичек один квадрат и два ромба.
2-28. Из 10 спичек составлены 3 квадрата. Одна спичка удаляется, а из оставшихся 9 спичек требуется составить три новых равных четырёхугольника.
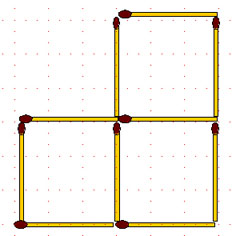
2-29. Как построить из 10 спичек два правильных пятиугольника и пять равных треугольников?
2-30. Переложите все спички на рисунке к задаче 2-28 так, чтобы образовалась фигура, содержащая 4 квадрата.
2-31. Из 12 спичек составьте три равных четырёхугольника и два равных треугольника.
2-32. Из 12 спичек составьте 12-угольник с прямыми углами.
2-33. Из 12 спичек составьте 5 квадратов.
2-34. Для составления одного равностороннего треугольника необходимо 3 спички (если их не ломать). Составьте 6 равносторонних треугольников, равных между собой, из 12 спичек. После этого переложите 4 спички так, чтобы образовалось 3 равносторонних треугольника, из которых только два были бы равны между собой.
2-35. Переложите 3 спички так, чтобы получились 3 квадрата.

2-36. Переложите 6 спичек так, чтобы получилось 5 квадратов.

2-37. Из 12 спичек сложены 3 квадрата со стороной, равной длине спички. Попробуйте из них сложить 6 единичных квадратов.

2-38. Переложите эти 12 спичек так, чтобы вдоль каждой стороны четырёхугольника их лежало не четыре, как сейчас, а пять.
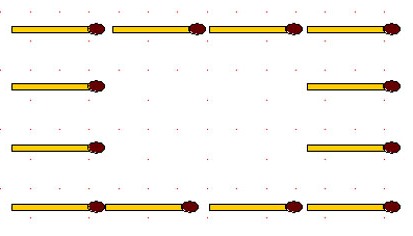
2-39. Изображённые на рисунке 12 спичек требуется переложить так, чтобы вдоль каждой стороны их было:
а) по 5 штук;
б) по 6 штук.

2-40. В фигуре, изображенной на рисунке к задаче 37:
а) переложите 5 спичек так, чтобы получилось всего 2 квадрата;
б) переложите 3 спички так, чтобы получилось 5 квадратов.
2-41. Из спичек сложите правильный шестиугольник и докажите с помощью дополнительного построения и путём рассуждений правильность построения.
2-42. В фигуре, показанной на рисунке:

а) переложите 3 спички так, чтобы вместо фигуры из 6 равносторонних треугольников получилась фигура их 6 равных четырёхугольников;
б) переложите 3 спички так, чтобы получилось 7 четырёхугольников, но на этот раз они могут быть не равные.
2-43. В фигуре, изображенной на рисунке:
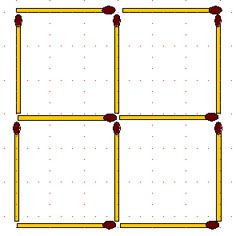
а) переложите 3 спички так, чтобы получилось 3 равных квадрата;
б) переложите 4 спички так, чтобы получилось 3 равных квадрата;
в) переложите 4 спички так, чтобы получилось 2 квадрата;
г) уберите 2 спички так, чтобы осталось 2 квадрата;
д) переложите 2 спички так, чтобы образовалось 7 квадратов (допускается наложение одной спички поперек другой);
е) переложите 4 спички так, чтобы получилось 10 квадратов;
ж) добавьте к исходной фигуре ещё 4 спички так, чтобы квадратов стало 9;
з) расположите те же 12 спичек (все спички должны лежать в плоскости стола) так, чтобы они ограничивали 5 квадратов, причём каждый квадрат должен быть пуст, в противном случае квадраты, изображенные на рисунке, могли бы служить решением, поскольку в качестве пятого мы могли бы считать большой квадрат. Не разрешается ни укладывать две спички одна на другую, ни оставлять свободные концы.
2-44. Спички расположены, как показано на рисунке. Переложите 2 спички так, чтобы получилось 5 равных квадратов.
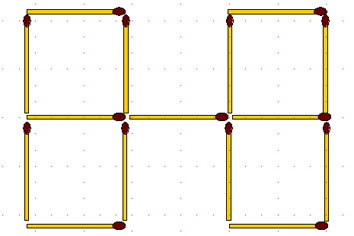
2-45. В фигуре, изображенной на рисунке:

а) снимите 3 спички так, чтобы получилось 3 равных квадрата;
б) переложите 4 спички так, чтобы получилось 3 не равных квадрата;
в) выложите из пяти малых квадратов три, переложив не более 10 спичек.
2-46. Из 16 спичек сложено 5 квадратов. Переложите 2 спички так, чтобы число квадратов уменьшилось на один.
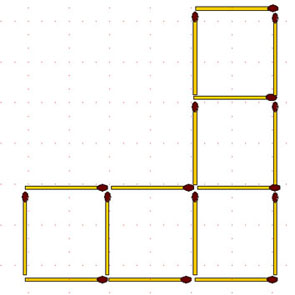
2-47. В пяти квадратах нужно переложить 4 спички так, чтобы получилось 4 квадрата равной величины.

2-48. Передвинув только 2 спички, постройте 4 одинаковых по размеру квадрата.

2-49. Уберите как можно меньше спичек так, чтобы оставшиеся спички образовали 4 равносторонних треугольника, таких же размеров, как и 8 треугольников в исходной конфигурации, и нигде не торчали свободные концы.

2-50. Уберите 5 спичек так, чтобы осталось только 3 квадрата.

2-51. Уберите 2 спички так, чтобы осталось только 4 квадрата.

2-52. Из 18 спичек, составляющих 6 равных квадратов, отнимите 2 спички так, чтобы осталось 4 таких же квадрата.

2-53. Из 18 спичек составьте:
а) пять квадратов;
б) один треугольник и 6 четырёхугольников по 3 двух разных размеров.
2-54. Из 18 спичек составьте шесть равных четырёхугольников и один треугольник, в два раза меньший по площади.
2-55. В фигуре, изображенной на рисунке:
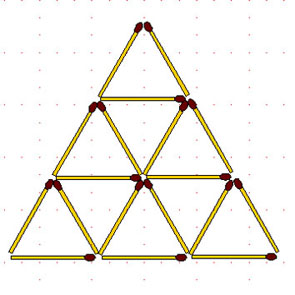
а) убрать 5 спичек так, чтобы осталось 5 треугольников (два решения);
б) переложить 6 спичек так, чтобы получилась фигура, составленная из 6 симметрично расположенных равных четырёхугольников.
2-56. Переложите 7 спичек так, чтобы получилось 4 квадрата.
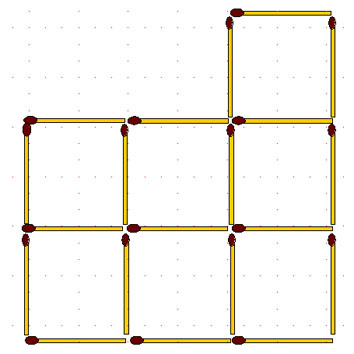
2-57. От 7 квадратов, которые образуют крест и составлены из 22 спичек, отнимите 6 спичек так, чтобы осталось 4 таких же одинаковых квадрата.

2-58. В изображенной фигуре, переложите 2 спички так, чтобы получилось 7 равных квадратов; затем, из полученной фигуры, уберите 2 спички так, чтобы осталось 5 квадратов.
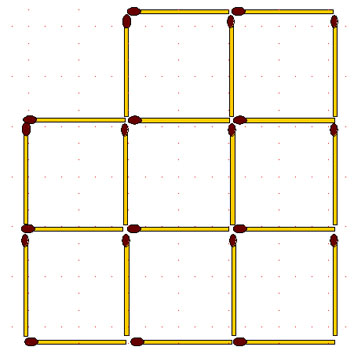
2-59. В фигуре, состоящей из 22 спичек:
а) убрать 4 спички так, чтобы образовалось 5 равных или 5 неравных квадратов;
б) убрать 6 спичек так, чтобы осталось 4 равных квадрата;
в) убрать 7 спичек так, чтобы осталось 4 равных квадрата.
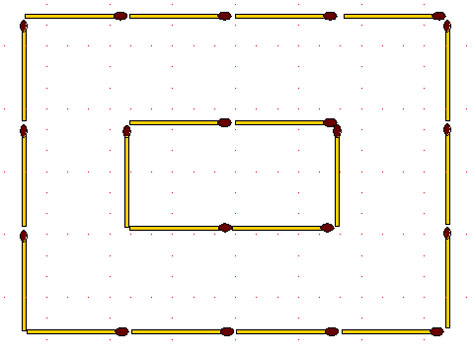
2-60. Представьте себе, что на рисунке изображен остров, окруженный каналом. Ширина канала как раз равна длине одной спички, так что перебросить мостик через канал с помощью одной спички нельзя: невозможно опереться концами о берег канала. Попробуйте построить мост через канал с помощью 2 спичек, не склеивая и не связывая их концы.
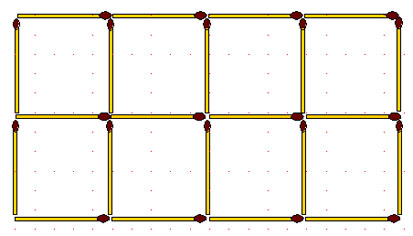
2-61. Уберите 4 спички так, чтобы оставшиеся спички образовали 5 квадратов, причём квадраты могут быть и не одинаковой величины.
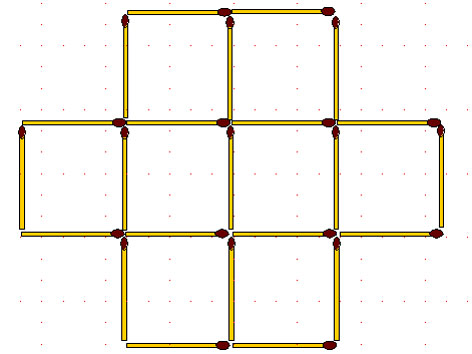
2-62. Уберите 3 спички так, чтобы оставшиеся образовывали 5 одинаковых квадратов.
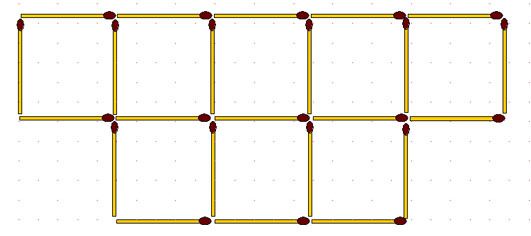
2-63. Переложите 16 спичек так, чтобы образовалось 4 маленьких квадрата в одном большом.

2-64. Из 24 спичек сложена фигура, для которой придумано много задач:
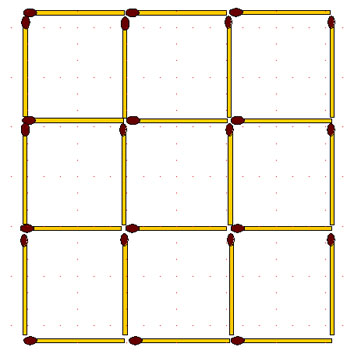
а) переложите 12 спичек так, чтобы образовалось 2 равных квадрата;
б) уберите 3 спички так, чтобы осталось 7 равных квадратов;
в) уберите 4 спички так, чтобы оставшиеся образовали один большой и 4 маленьких квадрата;
г) уберите 4 спички так, чтобы оставшиеся образовали один большой и 3 маленьких квадрата;
д) образуйте 5 равных квадратов, убирая : -4 спички; -6 спичек; -8 спичек;
е) уберите 5 спичек так, чтобы осталось 6 равных квадратов;
ж) уберите 6 спичек так, чтобы получилось 2 квадрата и 2 равных неправильных шестиугольника;
з) уберите 6 спичек так, чтобы из оставшихся образовалось 3 квадрата;
и) уберите 6 спичек так, чтобы из оставшихся образовалось 4 различных по величине квадрата;
к) уберите 8 спичек так, чтобы осталось только 2 квадрата (два решения);
л) уберите 8 спичек так, чтобы осталось 3 квадрата;
м) уберите 8 спичек так, чтобы осталось 4 равных квадрата (два решения).
2-65. Сколько одинаковых квадратов можно сложить из 24 спичек, не ломая их и используя при этом все спички?
А сколько квадратов можно образовать из 24 спичек, если считать при этом ещё дополнительные квадраты других размеров?
2-66. Убрать 10 спичек так, чтобы образовалось 4 равных квадрата. (Есть несколько различных решений).

2-67. Уберите 17 спичек так, чтобы осталось ровно 5 треугольников.

2-68. Экономный фермер для своих 16 коров соорудил треугольные загоны, используя 30 звеньев ограды (рис. предыдущей задачи).
Какое наименьшее количество звеньев ему приходится убирать по утрам, чтобы выгнать всех коров на пастбище?
2-69. У фермера было 32 звена ограды (32 спички), с помощью которых он соорудил загоны для своих 8 коров так, что на каждый загон ушло по 4 звена.

На следующий день он поумнел и перестроил загоны так, что обошелся только 25 звеньями. Ещё через день уменьшил количество звеньев на 3. Наконец, ему пришла в голову мысль, как можно обойтись всего 16 звеньями ограды, чтобы отгородить своё место каждой из 8 коров. Восстановите на спичках искания этого фермера, отгородив 8 загонов 25-ю, 22-я и 16-ю спичками.
2-70. На рисунке 13 одинаковых квадратов. Требуется убрать всего 4 спички так, чтобы осталось 8 равновеликих квадратов.

2-71. Спичками выложено 16 одинаковых квадратов. А сколько всего разных квадратов можно насчитать в этой фигуре? Какое минимальное количество спичек нужно убрать, чтобы оставшаяся фигура не содержала ни одного, ни большого, ни маленького квадрата?

2-72. Количество спичек, используемых в задачах, возрастает и вам уже не хватает одной коробки, но главное хватает ли терпения?
Уберите 24 спички так, чтобы осталось 4 маленьких квадрата в одном большом.
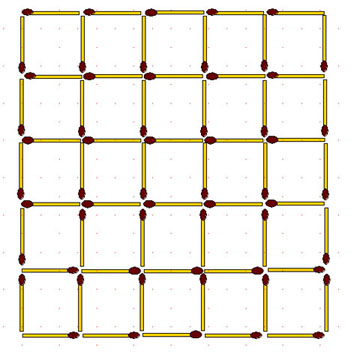
2-73. Из 63 спичек составлен большой треугольник и много маленьких.

Сколько всего различных треугольников можно насчитать в этой фигуре?
Уберите 36 спичек так, чтобы оставшиеся спички образовали 4 равных треугольника.
2-74. Уберите из фигуры 16 спичек так, чтобы осталось 12 равновеликих квадратов.

2-75. Спички на рисунке изображают волейбольную сетку. Какое наибольшее число спичек можно убрать, чтобы сетка при этом не распалась на отдельные части?

2-76. Сколько нужно спичек, чтобы построить фигуру, содержащую 60 квадратов, если разрешается накладывать спичку на спичку и считать квадраты всех размеров?
Сколько нужно спичек, чтобы построить фигуру, содержащую 100 квадратов?
Раздел Б. От геометрических фигур перейдем к изображению различных предметов.
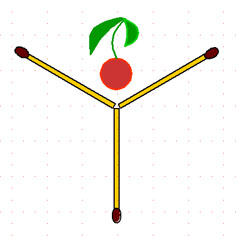
2-77. Бокал. Передвинув как можно меньше спичек, извлеките вишенку из бокала. Вишенку трогать запрещается.
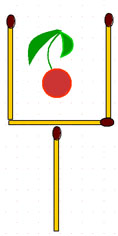
2-78. Рюмка. Решите такую же задачу для рюмки.
2-79. Рыба. Передвинув как можно меньше спичек, заставьте рыбу плыть в противоположном направлении.
2-80. Весы. Весы составлены из 9 спичек и не находятся в равновесии. Требуется переложить в них 5 спичек так, чтобы весы уравновесились.

2-81. Фонарь. Переложив 6 спичек, превратите фонарь в 4 равных треугольника.

2-82. Топор (рис. выше справа). Переложив 4 спички, превратите топор в 3 равных треугольника.
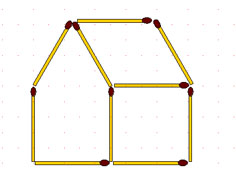
2-83. Дом. Из спичек построен дом. Переложите 2 спички так, чтобы дом повернулся другой стороной (фасадом направо).
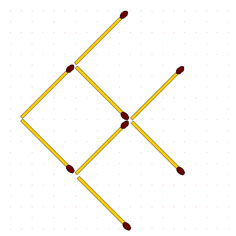
2-84. Летучая мышь (рис. слева ниже). Переложите 3 спички так, чтобы мышь летела в противоположную сторону.
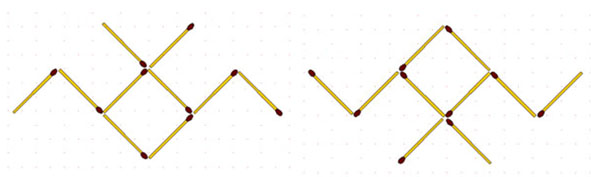
Рак (рис. справа выше). Эта задача может быть представлена в другом варианте. Спичечный рак ползёт вверх. Переложите 3 спички так, чтобы он пополз вниз.
2-85. Рюмки. Две рюмки составлены из 10 спичек. Переложите 6 спичек так, чтобы получился дом.

2-86. Флюгер (рис. ниже слева). Переложив 4 спички, превратите флюгер в дом.
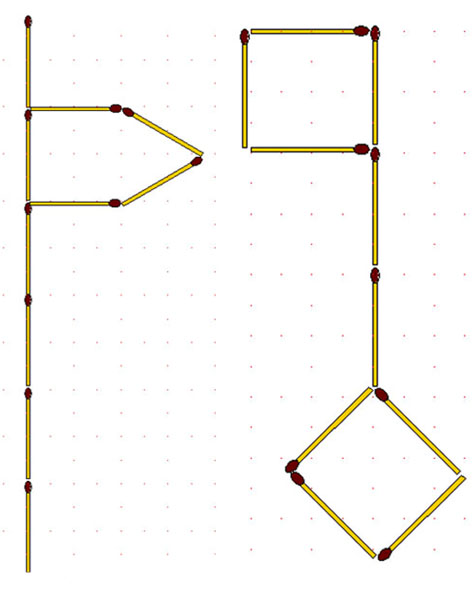
2-87. Ключ (рис. выше справа). Переложив 4 спички, превратите ключ в 3 квадрата.
2-88. Храм. Этот греческий храм сложен из 11 спичек.
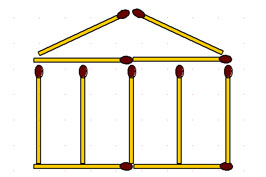
Требуется:
а) переложить 4 спички так, чтобы получилось 15 квадратов;
б) переложить 2 спички так, чтобы получилось 11 квадратов.
2-89. Лампа. Переложив 4 спички (рис. слева ниже), получите из настольной лампы 5 равновеликих треугольников.

2-90. Лампа-2 (рис. справа выше). В лампе, составленной из 12 спичек, переложите 3 спички так, чтобы получилось 5 равных треугольников.
2-91. Звезда и крест. Переложите у этой 12-конечной звезды 4 спички так, чтобы получился 4-конечный георгиевский крест.

2-92. Кресты. Получив в предыдущей задаче георгиевский крест, переложите в нём 8 спичек так, чтобы получился крест, состоящий из 4 крестов.
2-93. Во вновь полученном кресте, переложите 8 спичек так, чтобы образовалось 4 квадрата.
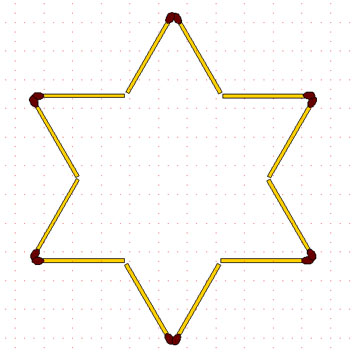
2-94. Звезда. Переложите в звезде 6 спичек так, чтобы получилось 3 равных и одинаково расположенных четырёхугольника.
2-95. Памятник. Требуется переложить 5 спичек так, чтобы получилось 3 квадрата.