Альтернативный волновой анализ
Еще один нюанс, влияющий на построение линейки Фибоначчи, – это значения, которые мы будем использовать в качестве опорных величин, т. е. то, что мы возьмем за 100 %.
Казалось бы, что здесь может быть непонятного? 0–100 %. Нет! Точнее, не всегда это так.
Иногда, например, намного лучше к текущей рыночной ситуации могут подходить несколько иные значения. Обратите внимание, что на нашем графике (см. рис. 2.5) в качестве опорной волны мы взяли значения 0–113 %, вместо 0–100 %. Ниже на рис. 2.6 я привел вероятностные значения ценовых экстремумов для расширяющейся формации, которые могут использоваться при выборе опорной волны, обозначенной цифрами (76,4–100–113 %). Также обратите внимание на то, что речь в данном случае идет о построении линейки Фибоначчи таким образом, что внутри опорной волны не должно быть никаких более мелких волн. Так как, если бы мы использовали именно такой способ (т. е. в качестве опорной волны взяли бы более крупное движение, и внутри оказалась вложенной мелкая коррекционная волна), то естественно, приведенные здесь значения были бы совершенно иными.
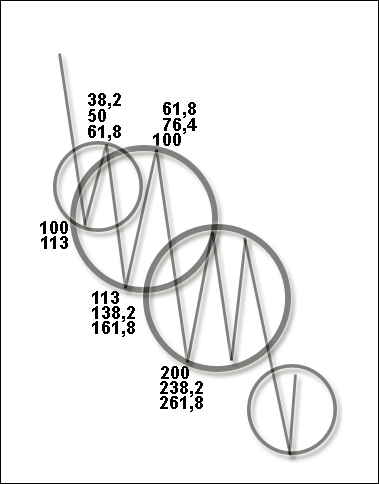
Рисунок 2.6. Вероятностные значения ценовых экстремумов для расширяющейся формации
Прежде чем мы продолжим рассматривать аналогичный пример вероятностных значений ценовых экстремумов, но уже для сужающейся волновой формации, я хотел бы сказать несколько слов относительно того, откуда возникли эти данные и насколько им можно доверять. Дело в том, что приведенные здесь значения являются эмпирическими, они получены мной в процессе обработки различных волновых структур, которые я специально для этих целей подбираю, а затем сохраняю в виде картинок в специальный файл уже длительное время.
Естественно, нужно понимать, что абсолютно все рыночные ситуации никто и никогда не сможет объединить в ограниченное количество волновых или любых других моделей. Аналогичный вывод можно сделать и относительно приведенных здесь цифровых значений для уровней коррекций. Ведь рынок намного более многообразен и сложен, нежели мы это себе представляем.
Тем не менее стоит отметить, что довольно часто (но не всегда) те соотношения, которые даны в примерах, позволяют получать достаточно точные значения величин коррекции, особенно в тех случаях, когда ситуация не находится в ожидании глобальных новостных факторов. Так как в подобной ситуации на рынке может произойти все что угодно! А что говорить о форс-мажорных событиях, которые вообще никак не прогнозируются заранее, хотя основной постулат технического анализа и утверждает, что «цена учитывает всё». Но это, конечно, все спорно.
Тем не менее возвращаемся к нашим значениям коррекции для сужающейся волновой конструкции (рис. 2.7).
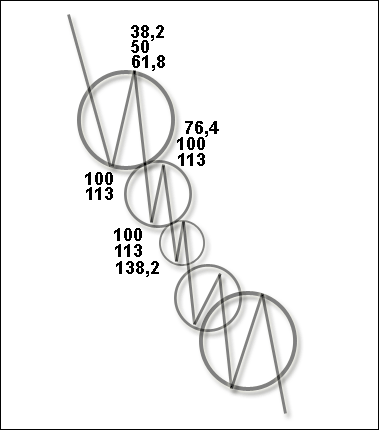
Рисунок 2.7. Вероятностные значения ценовых экстремумов для сужающейся формации
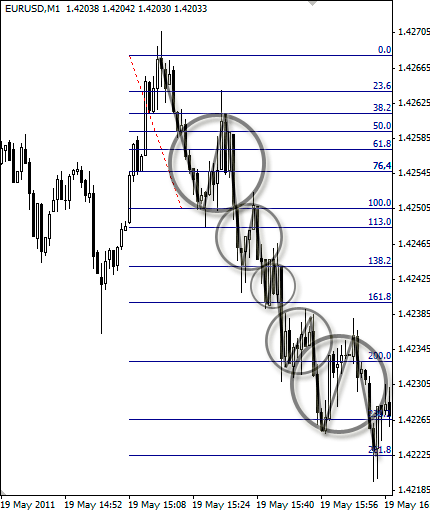
Рисунок 2.8. Пример графика с линейкой Фибоначчи
Вот таким образом я использую линейку для построения и дальнейшей фиксации волн на ценовом графике. Точно так же уровни коррекции Фибоначчи помогают не только выявить зоны поддержки и сопротивления, распознать волновую модель, определить вероятную область завершения корректирующей волны, но и, что самое главное, рассчитать точное значение для постановки отложенного ордера (рис. 2.8).
Линейка Фибоначчи и волновая разметка
Итак, в прошлой главе мы разобрались с вами, как используются коэффициенты «золотого сечения» на финансовых рынках. Теперь пришла пора закрепить материал на практических примерах. Но прежде чем мы перейдем непосредственно к работе с линейкой Фибоначчи, я хотел бы затронуть один болезненный вопрос, связанный с неоднозначностью в интерпретации волновых структур.
Как и все начинающие трейдеры когда-то, однажды я сталкивался с выражением о том, что волновой анализ является по своей природе очень субъективным, или, говоря простым языком, неоднозначным. Ведь действительно, разные аналитики, практикующие волновой анализ, могут по-разному трактовать одну и ту же рыночную ситуацию. С чем это может быть связано?
И я решил найти ответ на этот весьма непростой вопрос. Первое, что мне пришло в голову, разделить рынок на два состояния, когда он, с моей точки зрения, достаточно легко поддается прогнозированию, а когда нет. Поясню, о чем идет речь.
Ранее мы с вами уже говорили о том, что согласно волновому анализу, все финансовые рынки стремятся к равновесию, которое объясняется тем, что предложение стремится удовлетворить фактор спроса и наоборот. В результате происходит формирование таких ценовых волн, размеры которых соответствуют пропорциям «золотого сечения». Чаще всего такие «пропорциональные» волны хорошо прослеживаются тогда, когда на рынке не ожидается выхода важных фундаментальных новостей, способных нарушить хрупкое рыночное равновесие, или же, наоборот, тогда, когда новостные всплески уже компенсированы за счет спекулятивных рыночных сил.
Для того чтобы понять о чем идет речь, представьте себе резинку, которую сильно оттянули в какую-либо сторону. В результате такого воздействия она будет стремиться вернуться в исходное положение, так как на нее будут действовать соответствующие физические силы. Аналогичная ситуация может наблюдаться и на финансовых рынках, особенно в тех случаях, когда существенные колебания цены не подкреплены фундаментальной статистикой.
Из всего вышесказанного можно сделать следующий вывод: в тех случаях, когда на рынке не происходит сильных колебаний цены, связанных с новостными факторами, ценовое движение должно хорошо укладываться в пропорции Фибоначчи. Именно в таких ситуациях должен хорошо работать волновой анализ, а значит, неоднозначность в оценках экспертов должна быть минимальной.
Однако это еще не все, что я хотел бы добавить относительно субъективности волнового анализа. Другой аргумент, объясняющий наличие неоднозначности, связан, на мой взгляд, непосредственно с самим человеком и его методикой выделения волн. Кстати, именно поэтому линейка Фибоначчи, которую мы разбирали, должна быть обязательным инструментом для всех тех, кто желает научиться наносить волновую разметку на ценовом графике.
Поясню, что я имею в виду. Дело в том, что многие примеры волновых разметок, которые мне попадались на просторах сети Интернет, очень часто обладали одним схожим недостатком – практически на каждом из них присутствовала подгонка волн под определенную структуру. Это распространенное явление, когда у «эксперта» уже сформировалась некая картинка в голове, и он начинает выстраивать разметку так, как ему кажется «правильно», прибегая зачастую к явным манипуляциям с волнами.
В результате такой разметки, как правило, могут пропускаться существенные волны, и наоборот, выделяться малозначимые мелкие волны. Естественно, как вы понимаете, это в принципе не правильно, так как не отражает истинной сути происходящего на рынке и является одной из основных причин субъективизма.
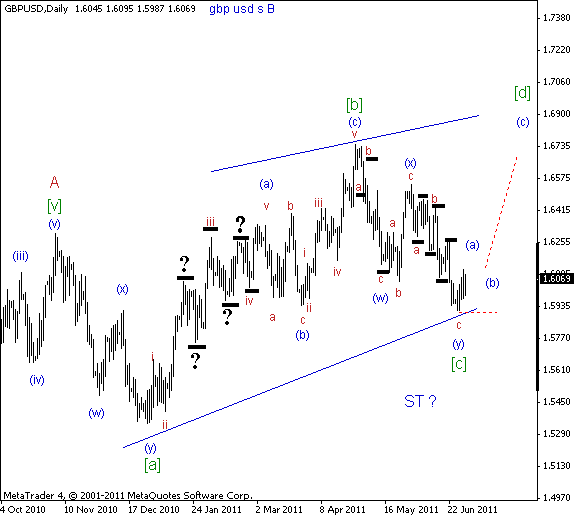
Рисунок 2.9. Волновая разметка пары GBPUSD известного в сети аналитика
Для того чтобы было понятно, о чем идет речь, разберем пример реальной разметки ценового графика пары GBPUSD, который я взял из сети Интернет (рис. 2.9). (Чтобы не вступать в конфликт с автором, я позволил себе удалить его имя с графика.)
Тем не менее вопрос остается прежним: давайте посмотрим на волну (а), где я горизонтальными отрезками с вопросительными знаками обозначил те волны, которые либо оказались совсем не участвующими в разметке, либо участвующими, но наполовину. Почему они остались не выделенными? Кстати, если вы внимательно просмотрите весь график, то найдете еще множество аналогичных примеров.
Однако не будем нападать на автора данной разметки, потому как такая особенность построения волновой разметки встречается чуть ли не у каждого второго сетевого аналитика. Я имею в виду тот факт, что в качестве одной коррекционной волны могут выделять очень малозаметное колебание на графике, в то время как другую коррекционную волну, превышающую предыдущую в несколько раз, при этом могут попросту пропустить, проигнорировав ее, потому что она не вписывается в «необходимую» волновую разметку. Но ведь это неправильно!
На мой взгляд, если вы используете волновой анализ, то как минимум необходимо стремиться к тому, чтобы коррекционные волны соответствующего ранга приблизительно совпадали в своих размерах и как максимум не допускать таких вещей, когда коррекционные волны абсолютно разных размеров относились к волнам одного порядка.
Для этих целей можно и нужно применять линейку Фибоначчи, что я, собственно говоря, и делаю в волновом анализе. Однако для того чтобы научиться это делать правильно, необходимо безошибочно научиться корректировать, а затем фиксировать линейку Фибоначчи на ценовом графике. Давайте посмотрим, как этого добиться.
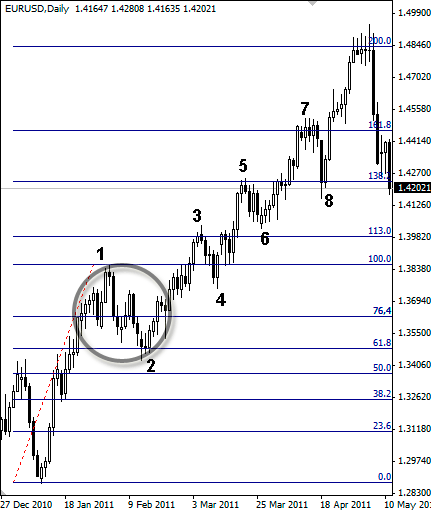
Рисунок 2.10. Первичное построение линейки Фибоначчи на ценовом графике
Для этих целей возьмем дневной график по паре EURUSD, а затем проанализируем, как нужно проводить построение и фиксацию уровней коррекции Фибоначчи с точки зрения волнового анализа (рис. 2.10).
Итак, для того чтобы построить линейку Фибоначчи с точки зрения альтернативного волнового анализа, первое, что нам понадобится – найти опорную волну, которую мы будем использовать затем, чтобы на ее основе строить линейку. Чаще всего такой опорной волной является первый существенный ход по направлению тренда. Кстати, именно такой ход я называю первой импульсивной волной. Итак, в качестве опорных точек мы выбрали первую импульсивную волну, которая в нашем случае представляет значительный рост евро против американского доллара в нижнем углу слева. Соответственно, этой волне мы должны задать начальные параметры 0–100 %, а дальше уже дело «техники», основная суть которой заключается в том, чтобы правильно произвести подстройку и дальнейшую фиксацию линейки Фибоначчи таким образом, чтобы совпало максимальное количество экстремумов на волновом графике. Кстати, сейчас наша линейка подстроена как раз не самым лучшим образом.
Откуда это видно и как это определить?
Для того чтобы научиться определять, правильно или нет произведена подстройка линейки Фибоначчи, необходимо исходить из текущей волновой структуры ценового графика. Обратите внимание на волны, которые я условно пронумеровал цифрами 3–4 и 5–6. Даже на глаз видно, что эти коррекционные волны имеют приблизительно одинаковые ценовые размеры, или, в крайнем случае, волна 3–4 чуть больше, чем волна 5–6. Но вот линейка Фибоначчи в данном случае утверждает обратное. Обратите внимание, что согласно текущему построению уровней коррекции, волна 3–4 теоретически должна находиться в диапазоне 100–113 %, а волна 5–6 располагаться внутри границ 113–138 %. Естественно, этого мы не видим, что означает, что мы неправильно построили нашу линейку. Давайте попробуем ее перестроить.
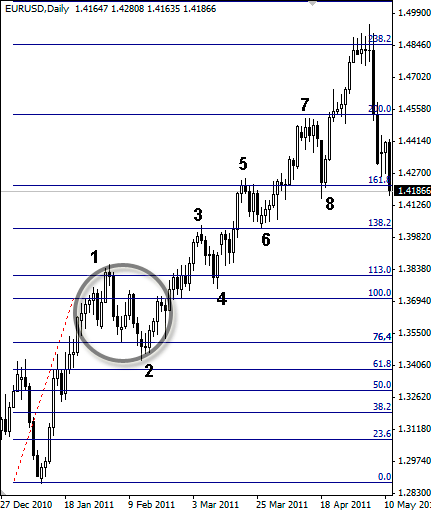
Рисунок 2.11. Корректировка и фиксация линейки Фибоначчи
Итак, подход второй. Теперь мы меняем цифровые обозначения нашей импульсивной волны со значений 0–100 % на значения 0–113 % (рис. 2.11). В результате такой подстройки мы видим, что большинство точек, которыми ранее мы пользовались для определения правильности построения уровней коррекции Фибоначчи, в данном случае достаточно хорошо совпали с указанными значениями диапазонов на линейке Фибоначчи. Давайте проверим их.
Самая первая коррекционная волна (1–2) в результате такой подстройки стала находиться в диапазоне – 113 % – 76 %, что приблизительно составляет ≈ 38 %. При расчете значений диапазонов я умышлено буду пользоваться «дискретными» значениями, в том плане, что эти значения также должны присутствовать на линейке Фибоначчи. Хотя в некоторых случаях точные величины этих диапазонов в некоторой степени могут отличаться от тех цифр, которые я буду приводить.
Продолжаем далее. Следующая коррекционная волна (3–4) достаточно точно вписалась в диапазон 138–113 %, что равняется ≈ 23 %. Примерно такую же величину занимает диапазон и следующей коррекционной волны, которая пронумерована цифрами (5–6). Ее диапазон колебания составил 161–138 % ≈ 23 %.
Ну и последняя коррекционная волна на участке роста – это откат с порядковым номером (7–8). Диапазон колебания этой коррекции был ограничен значениями 200–161 %, что приблизительно составило ≈ 38 %.
Таким образом, хорошо видно, что после корректировки линейки Фибоначчи гораздо большее количество экстремумов стало вписываться в наши границы. Та волновая конструкция, которую мы фиксировали на фазе роста, теперь подразделяется на четыре коррекционные волны, две из которых имеют приблизительный размер 23,6 %, а размеры двух других коррекций ограничены размерами 38,2 % (рис. 2.12).
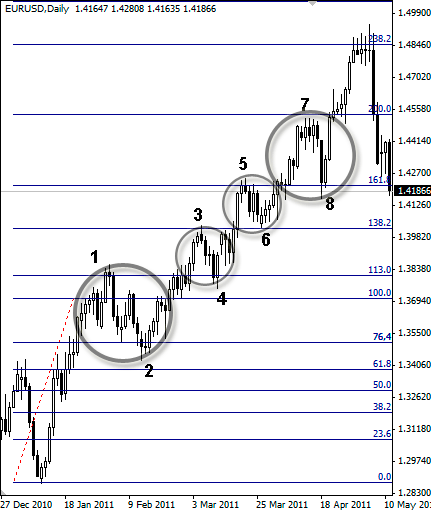
Рисунок 2.12. Пример значений Фибоначчи
В качестве заключения хочу еще раз отметить, что из всего многообразия инструментов, построенных на основе ряда чисел Фибоначчи и получаемых из него коэффициентов, на мой взгляд, только уровни коррекции Фибоначчи заслуживают особого внимания. Конечно, это всего лишь моя личная точка зрения и, возможно, многие не согласятся с ней. Тем не менее сколько я ни пытался применять все остальные инструменты Фибоначчи, ничего хорошего я из этого для себя не взял.
Глава II. Волновая разметка
Часть III. Нанесение волновой разметки
Фрактально-амплитудный способ нанесения волновой разметки
Для того чтобы окончательно закрепить наши знания и научиться правильно выделять ценовые волны на графиках, рассмотрим еще один способ нанесения волновой разметки, называемый фрактально-амплитудным способом. Для этого нам понадобятся индикатор fractals.
Вообще, фракталы используются в торговле по-разному. Кто-то, например, с помощью них строит наклонные и горизонтальные линии, другие трейдеры используют их в качестве ориентиров для определения величины стоп-лоссов, я же использую их для того, чтобы корректно и, что самое главное, единообразно отображать волновые конструкции. Поэтому разберем, что представляет собой фрактал. Построение фракталов есть автоматизированный процесс поиска ценовых экстремумов (максимумов и минимумов) при помощи встроенного алгоритма в торговой платформе MetaTrader4. Суть данного алгоритма заключается в простом использовании правила: две свечи выше/ниже до центральной свечи и две свечи выше/ниже после[2] центральной свечи (рис. 3.1).
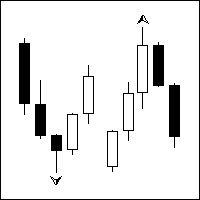
Рисунок 3.1. Фракталы
Например, верхний механический фрактал сформируется на ценовом графике тогда, когда максимальные цены двух предыдущих свечей были ниже текущего значения цены high, при этом две последующие свечи также будут иметь максимальные цены high ниже текущего значения максимума. Если вы посмотрите на свою ладонь, то средний палец, как раз будет тем пальцем, где должна будет формироваться метка фрактала. Тем не менее использование одних только механических фракталов на ценовом графике обычно не дает весомого преимущества по той простой причине, что многие из них оказываются «ложными».
«Ложными» означает тот факт, что они попросту не соответствуют истинным значениям экстремумов, которые затем можно было бы использовать с целью нанесения волновой разметки. Более того, не все из них в действительности определяют те ценовые точки, которые нам понадобятся для выделения волн и определения типа волновой модели. Таким образом, перед нами возникает задача постараться оптимизировать процесс построения фракталов, чтобы на их основе затем можно было сформировать правильную волновую разметку. Для этого будем использовать два основных правила:
• фильтрация механических фракталов величиной минимального шага (амплитуда);
• фильтрация механических фракталов правилом чередования.
Фильтрация механических фракталов величиной минимального шага необходима для того, чтобы отбросить незначительные ценовые колебания, возникающие чаще всего в диапазонах консолидации цен. Также этот фильтр позволяет нам варьировать степень детализации волновых моделей, которые мы собираемся искать на ценовых графиках, так как чем больше величина минимального шага, которую мы будем использовать, тем ниже степень детализации (ранг) волновых моделей мы будем получать. И, наоборот, чем меньше будет величина минимального шага, тем выше степень детализации волновых моделей мы получим.
И второй фильтр, который мы ввели, это правило чередования. Вообще, правило чередования является одним из наиболее важных правил классической теории волн Эллиотта. Оно нам понадобится для того, чтобы исключить некоторое количество ложных фракталов на ценовом графике. В качестве заключения мне хотелось бы добавить, что представленные здесь правила давно применяются на практике, и, прежде всего, моими учениками, во время изучения технического и волнового анализа. Давайте рассмотрим на примере, как работал бы данный способ, если мы возьмем часовой график пары AUD/JPY.
Итак, мы имеем механически расставленные значки экстремумов, выполненные при помощи индикатора «fractals». Наша задача определить, как заданные фильтры изменят имеющуюся картину, в результате чего мы должны будем получить волновую разметку этого ценового графика. Для этого зададим величину минимального шага и применим правило чередования. В качестве величины минимального шага я решил взять самую первую коррекцию, выделенную кругом и обозначенную экстремумами № 1 и № 2. Необходимо отметить, что данная величина будет являться тем минимальным значением волны (амплитудой), которую мы вообще будем фиксировать на ценовом графике. То есть любую волну меньшего размера мы учитывать не будем. Далее начинаем сравнивать длину сформировавшейся волны с заданным значением шага и отслеживать факт чередования экстремумов. Давайте рассмотрим на практике, как в процессе образования ценового графика формировались бы наши предположения об «истинности» или «ложности» фракталов, и соответственно, выстраивались волны.
Шаг № 1
Все сформировавшиеся на ценовом графике фракталы № 1–5 полностью соответствуют заданному нами алгоритму фильтрации.
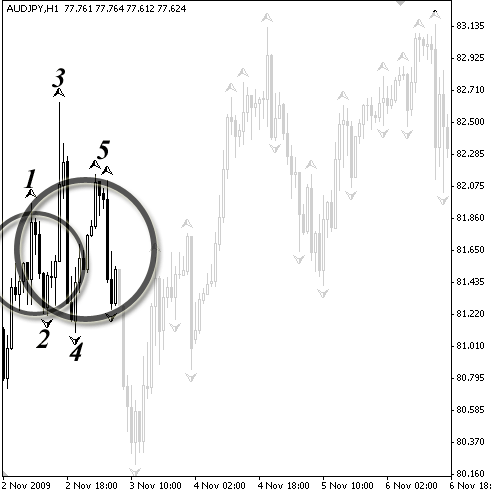
Рисунок 3.2. Шаг № 1
Каждая волна, которую они образовали, больше размера минимального шага, более того, безукоризненно выполняется правило чередования экстремумов: за пиком следует впадина, и, наоборот, за впадиной пик. Первая неувязка возникает после того, как за пятым фракталом появляется пик, в то время как, согласно правилу чередования, должна быть впадина (рис. 3.2).
Здесь наверняка напрашивается вопрос: почему за истинный экстремум взят первый фрактал, а не следующий за ним, хотя точки примерно одинаковые? Ответ следующий: если попадаются два рядом стоящих фрактала, лучше использовать более высокий экстремум для точки максимума и более низкий экстремум для точки минимума. Поэтому фрактал, следующий за пиком № 5, считаем «ложным», а значит, пропускаем его маркировку. Переходим к следующему шагу – второму.
Шаг № 2
После того как мы отбросили ложный фрактал возле максимума № 5, на ценовом графике образовался новый нижний фрактал, расположенный на окружности второго кольца, которое мы строили по точкам № 4–5. Этот фрактал удовлетворяет правилу чередования, и при этом образованная им медвежья волна также подпадает в диапазон нашего минимального размера (рис. 3.3). Казалось бы, все правильно, и можно зафиксировать порядковый номер этого ценового минимума. Однако необходимо проверить еще одно условие, которое обязательно должно выполниться. Речь в данном случае идет о размере минимального шага, но не только для текущей волны, но и последующей волны также. Поэтому, как только цена преодолевает уровень отмеченного фрактала, нумерация минимума аннулируется, а данный фрактал считается ложным.
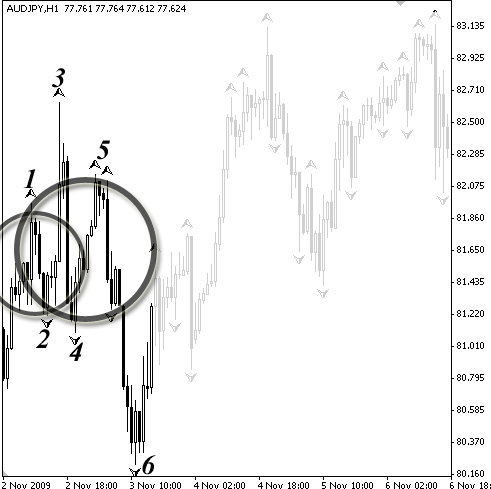
Рисунок 3.3. Шаг № 2
И только после того, как цена существенно снизилась, сформировав при этом новый нижний фрактал, мы можем продолжить нумерацию. В результате фиксируем фрактал № 6.
Шаг № 3
В текущем шаге интересным представляется формирование верхнего фрактала, который мы, согласно последовательности нумерации, обозначаем порядковым номером 7. Однако после того формируется медвежья коррекция, мы видим, что она не отображается снизу соответствующим нижним фракталом. Связано это с тем, что данный минимум не удовлетворяет критерию формирования механических фракталов (две свечи ниже до фрактала и две свечи ниже после фрактала). По этой причине программа, естественно, «упускает из вида» эту точку.
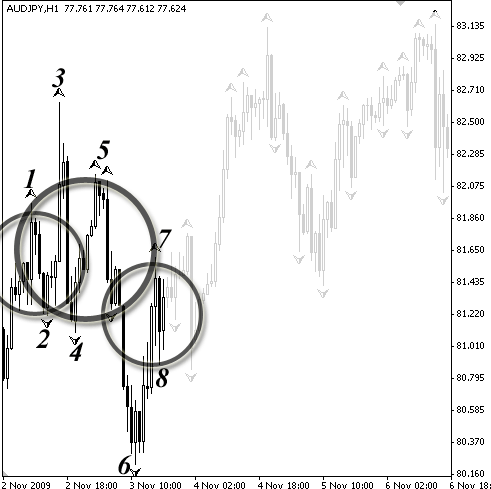
Рисунок 3.4. Шаг № 3
Тем не менее если приглядеться внимательно, в этой точке выполняются оба наших правила фильтрации: и правило чередования, и правило величины минимального шага. Таким образом, будем считать, что если в дальнейшем аналогичные точки будут нам попадаться, необходимо выделять их в качестве фракталов, и подвергать последовательной нумерации. В соответствии с этим запишем текущий минимум под № 8, а также построим круг-коррекцию (рис. 3.4).
Шаг № 4
Следующий шаг дает возможность отследить новый ложный фрактал, сформировавшийся на минимуме между фракталами № 8 и № 9. В данном случае он достаточно легко отфильтровывается, если мы применим правило чередования: после того как мы обозначили локальный минимум номером 8 и этот минимум продолжает «оставаться в игре», наша задача отслеживать, чтобы текущая волна была больше значения минимального шага, а также параллельно фиксировать появление нового верхнего фрактала. Однако в нашем случае появляется второй подряд нижний фрактал, который мы и вынуждены считать ложным. По мере формирования новых свечей на графике появляется верхний фрактал. Он удовлетворяет всем нашим критериям, поэтому считаем его истинным и соответственно маркируем цифрой 9. После этого идет стремительный ценовой спад, в результате чего мы регистрируем новый нижний фрактал, который обозначаем порядковым номером 10 (рис. 3.5).
В данном случае механические фракталы полностью соответствуют всем установленным фильтрам, что означает, что ложных экстремумов среди появившихся отметок нет.
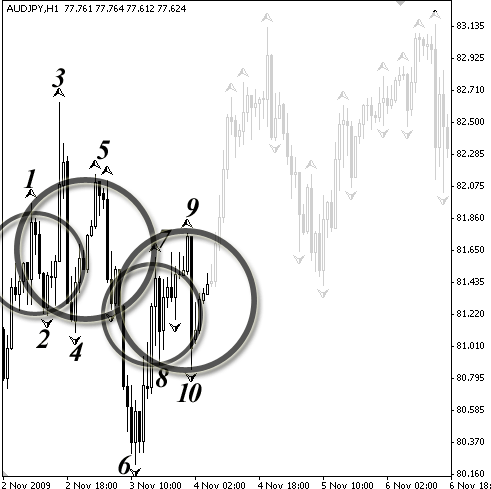
Рисунок 3.5. Шаг № 4
Шаг № 5
Для следующего шага, согласно правилу чередования, мы ожидаем появление верхнего фрактала. В данном случае минимальный размер волны выполняется, поэтому, как только появляется первый верхний фрактал, мы сразу его нумеруем фракталом № 11. Тем не менее спустя некоторое время формируется следующий, более высокий фрактал, следовательно, мы переносим нумерацию нашего 11 экстремума уже на этот фрактал, так как второй верхний фрактал оказывается выше первого. Еще через некоторое время цена вновь делает рывок вверх, в результате чего образуется уже третий верхний фрактал, после чего происходит движение цены вниз, на величину, превышающую размер заданного минимального шага. В соответствие с нашим правилом фильтрации снова передвигаем метку истинного фрактала на образовавшийся максимум и маркируем его номером 11. Теперь, если наш максимум сохранится, наша задача будет заключаться в том, чтобы зафиксировать уже новый ценовой минимум, или которому мы присвоим порядковый № 12 (рис. 3.6).