
Население Земли как растущая иерархическая сеть II
Например, чтобы подсчитать сколько людей проживало в 1700 году сначала находим число циклов до сингулярности Дьяконова – Капицы: (2022–1700)/40 = 8,05 цикла. Затем 1,1·4,3 миллиарда делим на 8,05 и получаем 590 миллионов человек.
* * *Средняя длительность инновационных циклов, так же как продолжительность глобальных исторических периодов Мир-системы, выражается через фундаментальную константу исторического времени τ по одной и той же формуле (обобщение гипотезы Й. Шумпетера):
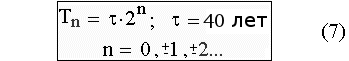
Рис. 3. Длительность экономических и глобальных исторических циклов, выраженная через квант исторического времени τ.
При этом продолжительность сокращающихся по закону прогрессии исторических периодов Дьяконова – Капицы может быть получена, если брать целые неотрицательные значения n в пределах от нуля до семи. Если же брать значения n > 7, то получаются периоды эволюции Homo sapiens, но расположение этих периодов на оси времени не отвечает данным палеоантропологии, т. е. применяемая феноменологическая схема перестает соответствовать действительности.
Отрицательные значения параметра n = -1, -2, -4 в формуле (7) задают среднюю длительность экономических циклов Кузнеца, Жугляра и Китчена. Любопытно, что при n = -9, -11, -14 получаем, причем с приличной точностью, для продолжительности коротких инновационных циклов: месяц, неделю и сутки соответственно.
В заключительной главе книги Виктора Феллера «Предположение о структуре истории» рассмотрена схема построения исторических циклов, «атомом» в которой являются» одни сутки исторического времени. Возможно, это случайное совпадение, но нельзя не отметить, что продолжительность инновационных циклов и циклов Дьяконова – Капицы может быть получена простым умножением времени обращения Земли вокруг своей оси в наше время (с момента своего возникновения 4.5 млрд лет назад из-за приливных сил Земля постепенно замедляла свое вращение) на двойку в некоторой целой степени.
* * *Теоретическая гипербола на рис. 1 наилучшим образом описывает рост численности населения мира от неолита до 1982 года, т. к. лучше всего соответствует работе Фёрстера, исследованиям С.П. Капицы, работе Мак-Эведи, Джоунса и Кремера, данным Остина и Брауэра. Это действительно так, поскольку, во-первых, постоянная Фёрстера, вычисленная по формуле С = k·K42τ = 1.89·1011, равна усредненному ее значению по всем этим работам (см. главу «Константы Капицы»). И, во-вторых, точки сингулярности (256·39.75 = 8154 +2022 = 10176) – также совпадают.
Почему формула на рис. 1 столь хорошо описывает рост населения Земли, какой циклический процесс с периодом τ задает главный исторический цикл и что определяет константа K – все это на данном уровне феноменологии так и остается неизвестным.
Что же такое сингулярность Дьяконова – Капицы?
В своей книге «Пути истории» И.М. Дьяконов рассматривает восемь фаз или ступеней исторического процесса: первобытную, первобытнообщинную, раннюю древность, имперскую древность, средневековье, абсолютистскую средневековую, капиталистическую и посткапиталистическую.
Фазы исторического развития периодизации Дьяконова хорошо соответствуют периодизации по алгоритму восьми шагов, см. таблицу 2. Причем первобытную фазу, относящуюся к позднепалеолитическому периоду, можно считать фазой за номером нуль в теоретической периодизации; далее идут восемь исторических периодов по алгоритму и семь фаз Дьяконова.
Различие в том, что в теории имеется период 1386–1704 гг., отсутствующий в периодизации Дьяконова. И, кроме того, капиталистическая и посткапиталистическая фаза у И.М. Дьяконова ограничены 1840–1950, 1952–?? гг., тогда как по алгоритму – это 1863–1942, 1942–1982 и 1982–?? гг. Что выглядит привлекательнее, т. к. эти периоды неплохо соответствуют Кондратьевским циклам.
Важно отметить, что И.М. Дьяконов никогда не относился к результатам своих исследований как к догме. Это характерно для всех его работ. Можно ли в таком случае периодизацию по правилу восьми шагов считать совпадающей в пределах небольшой погрешности с периодизацией Дьяконова?
Понятно, что любой ответ на этот вопрос субъективен, мы же твердо убеждены в том, что это действительно так, столь велико совпадение независимых экспертных оценок с расчетными данными. В таком случае сингулярность Дьяконова – Капицы можно определить следующим образом:
Сингулярность Дьяконова – Капицы (историческая сингулярность) – это точка сингулярности эмпирической гиперболы мирового демографического роста необходимая наряду с датой начала неолита для расчета периодов мировой истории по правилу восьми шагов. К этой предельной точке на оси времени сходятся сокращающиеся по закону прогрессии исторические циклы. И это тот невидимый рубеж, за которым мировой исторический процесс переходит на совершенно новый, неизведанный путь развития.
Исторических циклов, задававших нарастающий темп развития человеческой цивилизации на протяжении последних десяти тысяч лет, за сингулярностью Дьяконова – Капицы – больше не будет. Что же нас ожидает за сингулярностью?
Что за сингулярностью?
Несомненно только то, что с глобальными историческими циклами будет полностью покончено. Очевидно, за сингулярностью Дьяконова – Капицы их продолжение – невозможно. Но что будет с инновационными циклами?
Ответить на этот вопрос, находясь в рамках феноменологической, чисто описательной теории нельзя, т. к. непонятна сама природа цикличности. Однако похоже, что Кондратьевский цикл каким-то непостижимым образом определяет как инновационные циклы, так и исторические. В таком случае за сингулярностью инновационных циклов также не будет. Более того, за сингулярностью Дьяконова – Капицы могут закончиться и одиннадцатилетние солнечные циклы!
Уж очень непохоже это явление на регулярный физический процесс. Достаточно вспомнить минимум Маундера, достоверность которого считается доказанной, когда в течение 70 лет с 1645-го по 1715 год – пятен на Солнце практически не было совсем! За сингулярностью Дьяконова – Капицы закончится рост численности населения Земли, а сама эта численность устремится к некоторой предельной, асимптотической величине.
Этот рост численности от неолита и до второй половины XX века, несомненно, был связан с цикличностью исторического процесса, о чем говорит эффективность алгоритма восьми шагов, но природа этой связи в рамках предложенной феноменологической схемы остается без объяснения.
* * *Ускорение развития цивилизации, связанное с ростом населения Земли (эта функциональная связь, видимо, не является причинно-следственной), можно сравнить с ускорением состава на восьми последовательных участках железнодорожного пути.
Набор скорости продолжится и в ходе демографического перехода за сингулярностью Дьяконова – Капицы в течение еще одного цикла исторического времени. А затем, во второй половине XXI века, локомотив прогресса выйдет на магистраль (длина которой не определена) равномерного (не ускоренного) бескризисного развития.
Отсутствие ускорения в этой метафоре означает постоянство численности населения Земли, фиксированное энергопотребление, неизменность структуры сформировавшейся ноосферы; в последовательности: мифология, этика, эстетика, искусство, наука, техника, технология, сумма технологий – не будет новых членов. По сути, это будет КОНЕЦ ИСТОРИИ в привычном понимании смысла этого слова, т. е. как процесса циклического, ускоряющегося, качественно меняющегося, каким она, несомненно, во все времена и была: от неолита до наших дней.
Ускорения не будет, но темпы развития во всех областях человеческой деятельности будут максимальными, ранее невиданными – так что с концом роста численности населения Земли прогресс не закончится и творчество не исчезнет. Но грозит ли сингулярность какими-либо катастрофами? Никаких катаклизмов, связанных с завершением цикличности исторического процесса в 2022 году, ожидать не следует.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Примечания
2
Чтобы разобраться в феномене универсальной эволюции, Панов применяет… термодинамику! Для универсума, биосферы и ноосферы, не по аналогии вовсе, а в прямом термодинамическом смысле вводятся в рассмотрение такие понятия, как фазовый переход, масштабная инвариантность, фазовое пространство, точка бифуркации… Физикалистский, катастрофический подход к историческому, эволюционному процессу приводит Панова к апокалиптическим, абсурдным результатам.
Для неискушенного ума творчество Панова представляет несомненный вред уже только потому, что после прочтения его работ может возникнуть иллюзия, что эволюцию и историю можно описывать на языке термодинамики. Для искушенного ума знакомство с «трудами» Панова – напрасная трата времени.
3
https://www.amnh.org/explore/amnh.tv/(watch)/science-bulletins/human-population-through-time
4
Может ли все это быть простым совпадением?
5
Т. е. начинает копировать клаттеры уже скопированные в этом цикле.
6
Foerster, Mora, and Amiot 1960
7
Компьютерра № 27–28 от 1 августа 2007 года.
8
Два цикла характерного времени в приложении этой модели к явлению роста населения Земли, а не две операции самокопирования СИС.
9
В приложении этой математической модели к росту населения Земли можно предположить, что на каждом клаттере копируются некоторые «продвинутые» клаттеры-носители, т. е. «продвинутые» СИС-ы в данной упрощенной модели не имеющие ранга и являющиеся сетеобразующими клаттерами сети ранга нуль. К этим СИС-ам прикрепляются дозревшие (дети) или по какой-либо причине открепленные ранее (кома, клиническая смерть…), но восстановившиеся материальные носители из растущей мировой демографической системы.
10
Т. е. количество его связей становится максимальным.
11
https://ria.ru/20160713/1465314625.html
12
Все вычисления проведены с избыточной точностью. Казалось бы, время начала эволюции человека с точностью до года – это абсурд. Но смысл предлагаемой здесь гипотезы в том, что все стадии и этапы эволюции человека (и не только человека) определяются ростом иерархической сети. Мы считаем, что время начала каждого цикла должно выражаться с «абсолютной» точностью через фундаментальные физические постоянные.
13
Существует точка зрения, и ее сторонники приводят тому многочисленные примеры, что дихотомическая (парная) иерархия прослеживается на всех уровнях организации материи. [17]
14
http://avmol51.narod.ru/Kapitsa/knjazeva_belavin_kurkina.pdf
15
Эта чисто формальная попытка объяснения циклического ускорения исторического времени на основе лишь математики с синергетическим уклоном представляется совершенно бессмысленной.
16
http://www.demoscope.ru/weekly/2003/0139/analit02.php
17
https://pikabu.ru/story/sergey_kapitsa_istoriya_desyati_milliardov_3995327
18
«Пановская» частота фазовых переходов или, что то же самое, «коротаевская» скорость макроэволюционного развития таким показателем считаться не может. Подробнее см. далее: «Миф о пановско—коротаевской сингулярности».
19
О возможной связи циклической активности Солнца с циклами мировой истории см. ниже, а также главу «Фантазии на тему эволюции».
20
Значение Т0 в работах по гиперболическому росту выбирается из интервала 2022–2027 гг. По расчетам Фёрстера Т0 лежит в пределах 2022–2032 гг.
21
В 1976 году советские астрономы А.Б. Северный, В.А. Котов и Т.Т. Цап, работавшие в Крымской астрофизической обсерватории, открыли пульсации Солнца с периодом 160.0101 ± 0.0016 мин. Пульсации были слабыми и охватывали Солнце целиком. Согласно статистическому анализу временного ряда 19 тысяч вспышек, наблюдавшихся на Солнце в 1947–1980 гг., – период пульсации Солнца равен Р0 = 160.0101 ± 0.0001 мин; соответствующая частота n0 = 104.1601 ± 0.0001 мкГц.
Открытие было подтверждено исследователями из Стэнфордского университета США, причем в дальнейшем было отмечено, что колебания с таким периодом уверенно наблюдались у Солнца только в 1974–1983 гг. (Шеррер и Уилкокс, 1983; Котов, 1996).
Статистический анализ данных о частотах короткопериодических звезд показал, что не только Солнце, но и другие звезды некоторых типов также «настроены» в среднем на эту же частоту (Котов, 1985; Котов 1997). В 1994–2005 гг. В.А. Котов и В.М. Лютый, измеряя блеск ядра сейфертовской галактики NGC 4151, обнаружили колебания его яркости с периодом 160.0108(7) мин, т. е. с таким же, что у Солнца.
С учетом данных за 1968–1997 гг. было установлено, что период и начальная фаза осцилляций неизменны на протяжении 38 лет наблюдений за NGC 4151. Причем период этот не подвержен эффекту Доплера (!) и не зависит от красного смещения. Такой же эффект был обнаружен и у других внегалактических объектов, самый далекий из которых квазар ЗС 454.3 (Самый близкий – Солнце.)
При этом удивительным оказалось распределение начальных фаз. Из 26 внегалактических объектов у 15 фаза совпала в пределах ошибок с фазой колебаний яркости Солнца, а у оставшихся 11 оказалась сдвинутой на полпериода; иначе говоря примерно одна половина объектов колеблется в фазе с Солнцем, а другая – в антифазе.
Т. е. имеется парадоксальная согласованность колебаний яркости объектов, разделенных громадными расстояниями. Все это не укладывается в рамки обычных астрономических и физических представлений, поэтому открытые ими колебания авторы представляют как новый космологический феномен: «когерентную космологическую осцилляцию» [18].
24
На самом деле для коэффициента сжатия исторических периодов он получил величину e/(e – 1) = 0.583, которую странным образом округлил до 0.5, что соответствует показателю сжатия, равному двум (1/0.583 ≈ 1.7 ≈ 2). При этом автор «Парадоксов роста» не счел нужным упомянуть ни работу Ю.В. Яковца 1997 года, в которой этот показатель равен 1.8, что ближе к двойке, чем у него, ни нашу работу 2006 года, в которой он в точности равен двум.
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Всего 10 форматов