
Культурно-историческая психология волевого действия: От прогноза – к поступку
При том же числе т возможных событий (т. е. таких событий, которые наступили хоть раз в жизни модели) модель может содержать: ящиков первого порядка – т, ящиков второго порядка – m2, ящиков третьего порядка – m3,, ящиков n порядка – mn.
Так что в простой среде пользоваться ящиками высоких порядков нецелесообразно: процедура прогнозирования становится громоздкой и длительной, а выигрыш в точности может быть малым или даже совсем отсутствовать (если, например, среда представляет собой бернуллиеву последовательность, т. е. случайную последовательность, в которой вероятность возникновения того или иного события не зависит от предшествовавшего события).
Здесь мы сталкиваемся с тем, что стремление улучшить вероятностное прогнозирование приводит к чрезвычайно громоздкой модели памяти. А нельзя ли каким-либо образом несколько разгрузить память, не ухудшая результатов вероятностного прогнозирования? Нельзя ли запоминать не все в равной степени и даже кое-что совсем не запоминать? Вслед за этим сразу же возникает другой вопрос: что именно надо запоминать более основательно, чтобы сохранить способность к вероятностному прогнозированию?
Пусть наша модель запоминает не все, что поступит на ее вход, с одинаковой глубиной. До сих пор блок памяти системы имел на входе сигналы («внешние события»), а на выходе, в качестве конечного продукта, – вероятностный прогноз, который мог быть использован следующими блоками, осуществляющими преднастройку. Теперь же и сам блок памяти должен будет использовать свой «продукт» – прогноз.
Если произошло событие А, то с помощью ящика «А» подсчитывается Р(А) – вероятность того, что снова произойдет А, Р(В) – вероятность того, что наступит событие В…, Р(К) – вероятность того, что наступит событие К. Это и есть вероятностный прогноз.
Предположим, что после этого наступило событие Y – событие, вероятность наступления которого, согласно прогнозу, равнялась P(Y). Теперь, как мы уже писали выше, следует поставить карточку Y в ящик А. Но карточка ставится с разным «весом» в зависимости от степени неожиданности события Y, она ставится с коэффициентом 1— P(Y).
Назовем эту величину коэффициентом неожиданности. Если в прошлом опыте после А всегда следовало Y, то Р(Y) = 1 (субъективная «модель среды» точно соответствует среде). Тогда 1—Р(Y) = 0, т. е. повторно наступившее событие Y не запоминается, не загружает память. В жестко детерминированной среде модель перестает запоминать, как только «научается» безошибочно прогнозировать ход событий. Но, если среда изменится и наступит не то событие, которое прогнозировалось, это событие врежется в память с максимальным коэффициентом неожиданности 1–0 = 1. Каждое событие запоминается тем сильнее (т. е. оказывается труднее забываемым), чем более неожиданным (удивительным) было возникновение его в данный момент.
Вероятности ожидания сигналов или ситуаций могут меняться от Р = 1 до очень маленьких величин. Всегда ли субъект учитывает все значения вероятностей или он может работать более экономно?
Можно предположить, что преднастройка осуществляется лишь по отношению к действиям, адекватным такой ситуации, возникновение которой прогнозируется с вероятностью, превышающей некоторую минимальную величину Р0. Величина Р0 играет роль абсолютного порога вероятностного прогноза. К ситуациям, появление которых прогнозируется с вероятностью меньшей, чем Р0 преднастройка не осуществляется. Если Р0 = 1/10 (а из экспериментальных данных вытекает, что это примерно так), то при наличии равновероятных сигналов вероятностный прогноз достигает пороговой величины Р0 лишь при числе сигналов до 10; при большем числе сигналов вероятностный прогноз появления каждого из них меньше порогового. Если же сигналы возникают с неодинаковыми вероятностями, то среди них могут оказаться сигналы с Р>0,1, но число таких сигналов будет всегда меньше 10 – независимо от общего числа сигналов. А это значит, что, как бы велико ни было число возможных сигналов, при наличии порога Р0 организм упрощает ситуацию так, как будто число возможных сигналов не больше, чем 1/Р0 (т. е. не более 10 в приводимом примере). Наличие порога Р0 позволяет при большом общем числе альтернатив принимать во внимание при прогнозировании лишь небольшую часть (не более 1/Р0) наиболее вероятных альтернатив.
Различие в подготовке к действиям на два сигнала наблюдается лишь тогда, когда различие прогнозируемой вероятности появления этих сигналов достаточно велико, больше некоторого ΔР – дифференциального вероятностного порога. В частности, для выработки условного рефлекса выработка прогноза с Р = 1 не является необходимой (такая ситуация практически недостижима даже в эксперименте); достаточно, чтобы прогнозируемая вероятность подкрепления была близкой к единице (Р≥1–ΔР).
Описанная структура памяти отражает лишь одну ее сторону, но именно ту, которая позволяет понять, как из прошлого опыта создается прогноз будущего, как осуществляется вероятностное прогнозирование.
Подготовка к действию и значимость сигнала
В приведенной выше структуре памяти в основу прогноза кладется частота (вероятность) возникновения событий и их сочетаний. При этом другие характеристики событий принимаются одинаковыми. Между тем ясно, что в действительности и преднастройка, и реакция субъекта на события сильнейшим образом зависят от значимости этого события для субъекта. Рассмотренная выше ситуация, когда все события принимаются как равные по значимости, является искусственной – удобной для первоначального исследования, но отличной от ситуации в реальной жизни. Очевидно, что сообщение о том, что этажом ниже возник пожар, вызовет совсем иную по силе и быстроте реакцию, чем сообщение о том, что этажом ниже ветер выбил стекло в окне – даже в том случае, если априорная вероятность этих сообщений одинакова. Равновероятные события могут вызвать очень различную преднастройку и различные реакции. Два разных субъекта различно реагируют на одну и ту же ситуацию даже при одинаковой неожиданности ее возникновения, если эта ситуация имеет для них различную значимость.
Значимость – величина субъективная, различная для разных субъектов, да и для одного и того же субъекта меняющаяся в зависимости от различных обстоятельств и прежде всего от целей субъекта. Дать определение значимости очень трудно; вместе с тем реальность ее существования и влияния на реакции субъекта не вызывает никакого сомнения. Совокупность значимостей, достаточно постоянных для данного субъекта, составляет существенную характеристику его личности. Это выявляется в его индивидуальных реакциях, в его системе предпочтений. Так, один предпочитает провести вечер на концерте Баха, а другой – за столом с приятелями. Но, чтобы сравнить то и другое и решить вопрос о предпочтении, надо измерить предпочитаемые вещи в сравнимой системе единиц. Поскольку каждый осуществляет такое сравнение, можно предположить, что у субъекта имеется некая единая шкала оценки значимости для различных ситуаций. Такая шкала напоминает деньги – всеобщий эквивалент, единую систему для оценки самых различных предметов и благ, дающую возможность сравнивать их. Только наличие такой единой шкалы (меры) может обеспечить систему индивидуальных предпочтений, выборов. Мы здесь не будем рассматривать, как формируется индивидуальная система значимостей. Ясно, что она связана с опытом, включая воспитание, влияние социальной среды.
В эксперименте, в ситуации, значительно упрощенной, по сравнению со сложными жизненными коллизиями, удается показать, как значимость сигнала влияет на время реакции на этот сигнал.
В экспериментах, проведенных на 26 испытуемых (студентах 20–29 лет), с помощью цифровой лампы предъявлялась случайная последовательность сигналов— цифры 1 и 2 с заданными частотами (соответственно Pj и P). По инструкции испытуемый должен был в ответ на появление сигнала 1 возможно быстрее и без ошибок нажимать ключ левой рукой, а в ответ на сигнал 2 нажимать другой ключ правой рукой. Время реакции регистрировалось электрическим миллисекундомером, включавшимся при появлении сигнала и выключавшимся при правильном нажимании ключа (при этом происходило и выключение сигнала).
Эксперименты проводились с тремя последовательностями сигналов (по 120 сигналов в каждой), различавшихся вероятностями появления сигналов 1 и 2:
а) последовательность: Р1 = Р2 = 0,5;
б) последовательность: Р1 = 0,75; Р2=0,25;
в) последовательность: Р1 = 0,83, Р2 = 0,17.
В I серии опытов испытуемые получали обычную почасовую оплату, зависящую от времени занятости в эксперименте.
Во II серии опытов вводилась еще дополнительная плата за каждую быструю и правильную реакцию на сигнал 2, что делало этот сигнал более значимым для испытуемого. Эта дополнительная плата была неодинаковой в разных сериях и в целом обеспечивала примерно одинаковый выигрыш для всех трех последовательностей сигналов.
В экспериментах с одинаковой значимостью сигналов 1 и 2 (первая серия) время реакции на сигнал и доля ошибочных реакций оказались большими на маловероятный (редкий) сигнал и меньшими на высоковероятный (частый) сигнал.
В экспериментах с неодинаковой значимостью сигналов для испытуемого (вторая серия) оказалось, что при повышении значимости одного из сигналов (2) время реакции на него и доля ошибочных реакций отчетливо снижается. Приводим в таблице 1 результаты этих исследований.
Как видим из этих экспериментов, введение дополнительной платы за правильную и быструю реакцию на сигнал увеличивает значимость отдельного сигнала для субъекта, что сказывается на укорочении времени реакции на этот сигнал. Значимость здесь формируется системой вознаграждений (или наказаний) за определенные реакции.
Повышение значимости сигнала для субъекта через увеличение вознаграждения (платы) за быструю и правильную реакцию на этот сигнал ведет к укорочению времени реакции на этот сигнал и к уменьшению числа ошибок на более значимый сигнал. При наличии двух сигналов, имеющих разную значимость для субъекта, время реакции на редкий (маловероятный) сигнал может не только сравняться с временем реакции на частый (высоковероятный) сигнал, но (при достаточном разведении вероятностей появления сигналов) даже стать более коротким, чем время реакции на частый, но менее значимый для субъекта сигнал.
Таблица 1
Время реакции и процент ошибочных реакций на сигналы одинаковой и неодинаковой значимости
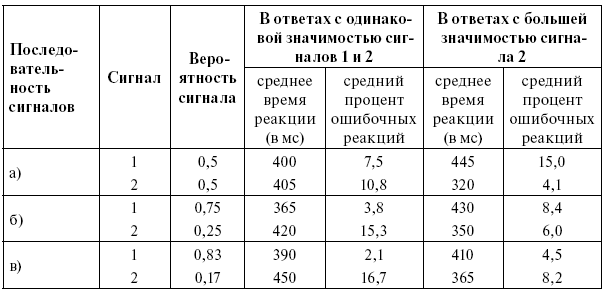
Таким образом, время реакции зависит не только от частоты (вероятности) сигнала, но и от его значимости. Это было, в частности, хорошо показано в работе А. Н. Леонтьева и Е. П. Кринчик (47, 48), в которой редкий, но значимый («аварийный») сигнал вызывал быструю реакцию испытуемого.
Вместе с тем необходимо подчеркнуть, что исследование зависимости времени реакции от значимости сигнала принципиально отличается от исследования зависимости времени реакции от частоты сигнала. Частоту сигнала экспериментатор может задать, а затем проследить, как зависит от нее время реакции. Частота сигнала – объективная величина. Значимость же не может быть полностью задана экспериментатором. Одно и то же событие имеет разную значимость для разных субъектов. Исследователь может судить о значимости только по реакциям испытуемого. В условиях эксперимента исследователь может менять лишь оплату (вознаграждение или наказание) за реакции испытуемого. Но плата и значимость – не одно и то же. Значимость – лишь функция платы. При этом значимость – нелинейная функция платы. При очень маленьких платах значимость почти не меняется с изменением платы. Затем с ростом платы наступает участок прямой и отчетливой зависимости значимости от платы. При очень высокой плате, по-видимому, дальнейшее изменение платы почти не влияет на значимость.
Формализовать понятие значимости во всей сложности не представляется нам возможным, по крайней мере, в настоящее время. В этом отношении мы должны присоединиться к мнению Ф. В. Вассина относительно трудностей формализации «значения – для субъекта», личностного смысла (А. Н. Леонтьев).
Тем не менее для более ограниченных задач, для частного круга простых ситуаций могут быть сделаны попытки формализации понятия значимости.
Пусть стимулы SA и SB, требующие соответственно реакций RAи RB, следуют в случайном порядке с равными вероятностями РА и PB. Если в этих условиях время реакции на эти стимулы ТА и TB оказываются одинаковыми, то естественно считать, что оба стимула имеют одинаковую значимость для субъекта.
Если в тех же условиях время реакции на один из стимулов оказывается меньшим (TA
Если мы имеем дело с двумя стимулами SA и SB неодинаковой значимости, то можно подобрать такое соотношение их частот РА и PBв случайной последовательности сигналов, при которой времена реакции ТА и TB окажутся одинаковыми. 0 возможности такого подбора вероятностей появления стимулов говорят описанные выше эксперименты, из которых следует, что при неодинаковой значимости стимулов время реакции на маловероятный стимул может не только сравняться, нот даже стать меньше, чем время реакции на высоковероятный стимул.
Пусть для уравнивания времени реакции ТА и TB понадобилось так изменить вероятности стимулов, что вероятность менее значимого стимула в n раз больше, чем вероятность более значимого (PB=nРΔ). Можно условиться считать, что в этом случае стимул SA в п раз более значим для субъекта, чем стимул SB.
Такая метрика определения значимости является условной, но она и не может быть абсолютной.
Эта попытка формализации понятия значимости применима лишь в очень ограниченном круге явлений и не может быть распространена на широкий круг многообразных и разнородных психологических феноменов, в которых выступает значимость тех или иных явлений для субъекта. Такой широкий подход к изучению значимости ждет еще как теоретического, так и экспериментального исследования.
Заключение
Быстрота и целесообразность реакций субъекта при возникновении тех или иных ситуаций или сигналов в значительной мере зависят от предварительной подготовки к этим реакциям еще до того, как возникла соответствующая ситуация. Подготовка осуществляется по отношению к тем реакциям, которые целесообразны (соответствуют целям субъекта или удовлетворению его потребностей) в ситуациях, прогнозируемых как наиболее вероятные. Вероятностное прогнозирование основано на прошлом опыте субъекта и возможно лишь при сохранении в памяти субъекта вероятностно упорядоченных следов минувших событий, вероятностно организованного прошлого опыта.
Описывая в этой главе модель такой вероятностно организованной памяти, на которой может основываться вероятностное прогнозирование, мы стремились показать, что даже сравнительно несложно организованная система упорядочения информации о прошлом опыте может быть достаточной для вероятностного прогнозирования предстоящих событий.
Неодинаковая значимость для субъекта различных событий отчетливо влияет на характер его реакций.
Изучение значимости событий для субъекта представляется в вышей степени актуальным. Оно затрудняется сложностью проблемы, отсутствием четкого определения значимости, принятого достаточно большим числом исследователей.
Однако для ограниченного круга сравнительно простых ситуаций возможна некоторая формализация понятия значимости и установление принципов ее измерения. В этой главе такая попытка сделана применительно к области измерения времени реакции в ответ на сигналы, следующие в случайной последовательности.
Глава III
Условная и ориентировочная реакции как опережающие реакции при различной степени неопределенности прогноза
Понятие «ориентировочная реакция», как это нередко бывает с научными терминами, проделало определенную эволюцию. Если И. П. Павлов понимал под этим термином рефлекс «что такое?» – комплекс изменений, связанный с установкой органов чувств при неожиданном воздействии раздражителя, то теперь в комплекс изменений, обозначаемый термином «ориентировочная реакция», многими авторами включается также десинхронизация электрической активности мозга, возникновение неспецифического ответа в виде «вертекс-потенциала», колебание электрического потенциала кожи (КГР), изменение мышечного тонуса, некоторые вегетативные сдвиги. Мы будем здесь пользоваться термином «ориентировочная реакция» в этом широком смысле, не вдаваясь в обсуждение того, насколько удачным он является.
При делении реакций на условные и безусловные ориентировочная реакция оказывается в каком-то промежуточном положении: она, как и безусловные, не требует предварительной выработки, но, как условные, связана с индивидуальным прошлым опытом (например, ее угасание при потере раздражителем «новизны»). На связь ориентировочных и условных реакций указывает и тот факт, что вторые особенно хорошо вырабатываются на те сигналы, которые вначале вызывают сильную ориентировочную реакцию (Соколов, 1958). При выработке условного рефлекса между ним и ориентировочной реакцией возникают своеобразные «ножницы»: условная реакция усиливается, а ориентировочная ослабевает. Создается впечатление, что это две «антагонистические» реакции.
Попробуем, однако, рассмотреть эти две реакции как разные стороны единого процесса.
Избирательность подготовки к действиям и неопределенность прогноза
Мы исходим из представления о том, что на основе прошлого опыта субъект способен прогнозировать (экстраполировать) дальнейшие изменения среды на некоторый отрезок времени. Прогноз относительно наступления определенных событий и соответствующих им действий всегда носит вероятностный характер: одни события и действия ожидаются с большей, другие – с меньшей вероятностью. В соответствии с прогнозом субъект осуществляет подготовку к ожидаемым действиям, активируя одни и притормаживая другие системы.
В ситуации определенного прогноза, когда можно почти однозначно предсказать наступление определенного события, субъект получает возможность осуществлять действие раньше, чем появится ситуация, по отношению к которой это действие является адекватным (условный рефлекс).
В условиях неопределенного прогноза осуществляется подготовка к нескольким возможным действиям – чем больше степень неопределенности прогноза, тем больше систем должно быть подготовлено к действию. Такой предварительной подготовкой систем в ситуации неопределенного прогноза и является ориентировочная реакция.
В этой главе делается попытка рассмотреть ориентировочную и условную реакции как опережающие реакции в условиях различной степени неопределенности прогноза. С этой целью нами была проведена серия экспериментов, в которых изучались особенности преднастройки в ситуации определенного и неопределенного прогноза.
Методика исследования состояла в следующем. Испытуемому давали инструкцию реагировать возможно быстрее движением правой руки на появление светового квадрата и движением левой руки – на появление светового треугольника. Испытуемому сообщали, что перед световыми сигналами будет подаваться сигнал «внимание» (звук длительностью 1,5–2 с). Спустя 1,5–2 с после включения звука на табло появлялся один из световых сигналов. Следующая пара сигналов (звук и свет) подавались через 8—15 с. Было проведено две серии опытов. В одной серии опытов (серия А) испытуемому предъявлялись два световых сигнала в случайном порядке с равной вероятностью (P1 = P2 = 0,5), во второй серии (В) после сигнала «внимание» появлялся только один из световых сигналов (либо квадрат, либо треугольник) с Р = 1. Для половины испытуемых опыт начинался с серии А (50 сигналов), после чего без предупреждения испытуемому начинал предъявляться каждый раз только один из световых сигналов (серия В). Для другой половины испытуемых опыт проводился в обратном порядке – сначала серия В, а потом серия А. В течение опыта непрерывно регистрировались: на ЭЭГ – биоэлектрическая активность затылочной области правого полушария и сенсомоторных областей обоих полушарий; на ЭМГ – биоэлектрическая активность локтевых разгибателей кисти обеих рук или глубоких сгибателей пальцев. Со стопы левой ноги регистрировалась КГР (по Тарханову). В опыте участвовало 20 здоровых испытуемых.
Регистрация основного ритма ЭЭГ затылочной области и сенсомоторных областей обоих полушарий показывает, что первые 8—10 предъявлений сигналов вызывают депрессию основного ритма, начинающуюся при включении сигнала «внимание» (звук) и исчезающую спустя 2–3 с после предъявления светового сигнала. На ЭМГ в интервале времени от выключения звука до предъявления светового сигнала, когда движение отсутствует, наблюдается биоэлектрическая активность примерно одинаковой амплитуды (5—20 мкв) на обеих руках. В начале опыта регистрируются также КГР на звук и на световые сигналы.
В ходе опыта характер наблюдаемых реакций меняется. КГР на звук быстро угасает (через 5—10 предъявлений) и в том случае, когда предъявляется два световых сигнала после звука (серия А) и когда предъявляется один и тот же световой сигнал (серия В). На световые сигналы КГР начинает возникать с меньшим латентным периодом (спустя 0,5–1 с, а иногда в момент предъявления светового сигнала). Когда предъявляется один и тот же световой сигнал (серия В), то КГР на него постепенно угасает: на 3–5 десятке световых сигналов КГР наблюдается в среднем 2,6–1,5 раза на 10 предъявлений сигналов. Когда предъявляются два световых сигнала в случайном порядке (серия А), то КГР на них почти не угасает: в этом случае на 3-5-м десятке сигналов КГР наблюдается в среднем 7–8 раз на 10 предъявлений сигналов.
Возникновение депрессии основного ритма на ЭЭГ в ходе опыта смещается с начала действия звука к моменту предъявления светового раздражителя. Депрессия основного ритма на ЭЭГ в ходе опыта все чаще начинает возникать не на появление сигнала «внимание», а либо в конце действия звука, либо в интервале времени между выключением звука и появлением пускового стимула (рисунки 2–3). Депрессия на световой сигнал укорачивается при этом до 1–1,5 с.
На ЭЭГ затылочной области депрессия основного ритма после смещения во времени возникновения постепенно угасает в интервале от выключения звука до предъявления светового сигнала. На 3-5-м десятке предъявлений сигналов депрессия на ЭЭГ затылочной области в интервале между звуком и светом наблюдается в среднем 4–6 раз на 10 предъявлений сигналов, независимо от того, один или два световых сигнала предъявляются в опыте (т. е. в серии Ли в серии В). На световые сигналы депрессия на ЭЭГ затылочной области угасла только у 3 испытуемых из 20.
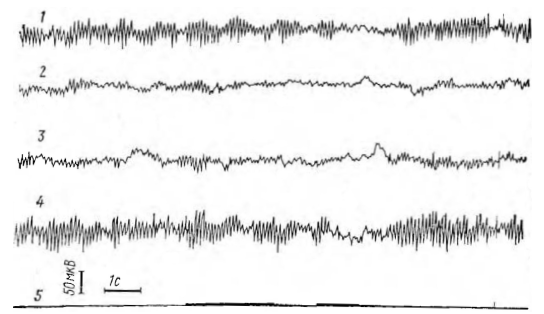
Рис. 2. ЭЭГ-реакция испытуемого А. В. на 31-е предъявление сигналов в серии А. После предупреждающего сигнала предъявляются в случайном порядке два пусковых стимула с равной вероятностью (Р1=Р2=0,5).
Обозначения: 1 – запись затылочной области, 2 – сенсомоторная область левого полушария, 3 – сенсомоторная область правого полушария, 4 – теменно-затылочная область, 5 – отметка раздражителя: первая отметка – предупреждающий сигнал (звук), вторая – пусковой стимул (свет)
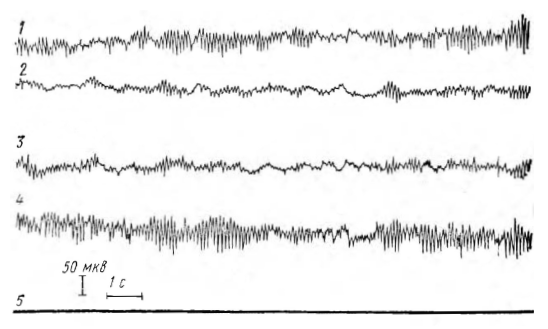
Рис. 3. ЭЭГ-реакция испытуемого А. В. на 49-е предъявление сигналов в серии В. После предупреждающего сигнала предъявляется один пусковой стимул (Р2 = 1, Р2=0). Обозначения те же, что и на рисунке 2
Когда предъявляются два световых сигнала (серия А), депрессия основного ритма на ЭЭГ сенсомоторных областей обоих полушарий, возникая либо в конце действия звука, либо в интервале времени между выключением звука и предъявлением светового сигнала, не угасает до конца опыта, наблюдаясь на 3-5-м десятке сигналов в среднем 8–9 раз на 10 предъявлений сигналов. Если же после звука предъявляется один и тот же световой сигнал (серия В), то до конца опыта не угасает только депрессия на ЭЭГ сенсомоторной области полушария, контрлатерального той руке, которой испытуемый реагирует на предъявляемый световой сигнал. Депрессия на ЭЭГ сенсомоторной области другого полушария в этой ситуации постепенно угасает у половины испытуемых, наблюдаясь у них в конце опыта (31-50-й сигналы) 5–6 раз на 10 предъявлений, сигналов; у другой половины испытуемых депрессия на ЭЭГ полушария, контрлатерального неработающей руке, практически не угасает, наблюдаясь 8-10 раз на 10 предъявлений сигналов в ситуации, когда после звукового сигнала каждый раз предъявляется один и тот же световой сигнал.

