От микроорганизмов до мегаполисов. Поиск компромисса между прогрессом и будущим планеты

Ни одно дерево не растет до небес, как и ни один артефакт, структура или процесс; и модели ограниченного роста характеризуют развитие машин и технических возможностей так же, как описывают рост населения и расширение империй. Все процессы распространения и внедрения неизбежно должны соответствовать этой модели: не важно, быстрый или медленный рост демонстрирует траектория на начальном этапе – в конце концов за ним последует значительное замедление темпов роста по мере того, как процесс асимптотически приближается к насыщению и часто достигает его (иногда после многих десятилетий распространения) всего за несколько процентов, даже за доли процентов до максимума. В 1880 году ни в одном доме не было электричества, но сколько зданий в городах Запада не подключено к электричеству сегодня?

Учитывая распространенность феноменов, демонстрирующих ограниченный рост, неудивительно, что многие исследователи стремились вписать их в разнообразные математические функции. Два основных класса траекторий ограниченного роста включают S-образный (сигмоидальный) и ограниченный экспоненциальный рост. В десятках работ даны описания оригинальных производных и последующих модификаций этих кривых. Они рассмотрены в обширных обзорах (Banks, 1994; Tsoularis, 2001), а лучший обзор, пожалуй, приведен в таблице S1 у Мирвольда (Myhrvold, 2013), где систематически сравниваются уравнения и ограничивающие условия для более 70 нелинейных функций роста.

S-образные функции описывают множество естественных процессов роста, а также внедрение и распространение инноваций, будь то новые промышленные методы или потребительские товары. Изначально медленный рост ускоряется в точке нижнего изгиба, за которым следует быстрый подъем, темп которого в конце концов замедляется, формируя второй изгиб, за которым следует замедленный подъем, так как рост становится минимальным и значения приближаются к максимальной границе конкретного параметра или к полному насыщению рынка. Наиболее известная и распространенная функция с S-образной траекторией описывает логистический рост.

В отличие от экспоненциального (неограниченного) роста, увеличение темпа которого пропорционально текущему значению, относительное приращение логистического (ограниченного) роста уменьшается по мере приближения растущего значения к максимально возможному уровню, который в экологических исследованиях обычно называют предельной нагрузкой. Подобный рост интуитивно кажется нормальным:

Обычно население медленно растет с асимптотического минимума, затем быстро множится и медленно движется к нечетко определенному асимптотическому максимуму. Два конца кривой роста населения в целом определяют всю кривую между ними: чтобы так начаться и так закончиться, кривая должна пройти через точку перегиба, это должна быть S-образная кривая (Thompson, 1942, 145).

Формальное определение логистической функции восходит к 1835 году, когда Адольф Кетле (1796–1874; рис. 1.9), бельгийский астроном и в то время ведущий статистик Европы, опубликовал революционную работу под названием Sur l’homme et le développement de ses facultés, ou Essai de physique sociale («О человеке и развитии его способностей, или Эссе по социальной физике»), где отметил невозможность продолжительного экспоненциального роста любого населения (Quetelet, 1835).

Кетле предположил, что силы, противоположные неограниченному развитию и росту населения, возрастают пропорционально квадрату скорости, с которой оно возрастает, и попросил своего ученика, математика Пьера Франсуа Ферхюльста (1804–1849; рис. 1.9), дать формальное решение и затем применить его к лучшим доступным статистическим данным. Ферхюльст согласился и сформулировал первое уравнение, выражающее ограниченный рост населения в короткой публикации в альманахе Correspondance Mathématique et Physique («Работы по математике и физике») (Verhulst, 1838; перевод на английский язык опубликован Vogels et al., 1975). Логистическая модель описана с помощью дифференциального уравнения

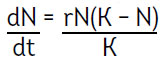
где r – скорость максимального роста, а K – максимально достижимая величина, известная в исследованиях экологии и населения как предельная нагрузка.

Рис. 1.9. Адольф Кетле и Пьер Франсуа Ферхюльст. Гравюра на стали из коллекции изображений XIX века, принадлежащей автору

Чтобы проверить возможность применения уравнения роста, Ферхюльст сравнил ожидаемые результаты с относительно короткими периодами данных переписей населения во Франции (1817–1831), Бельгии (1815–1833), графстве Эссекс (1811–1831) и России (1796–1827), и хотя он обнаружил «очень точное» совпадение с данными по Франции, он сделал верный вывод (учитывая малый объем данных), что «только будущее откроет нам истинный образ действий сдерживающей силы…» (Verhulst, 1838, 116). Семь лет спустя в более объемной работе он решил «назвать кривую логистической» (Verhulst, 1845, 9). Он никогда не объяснял, почему назвал ее именно так, но в период его жизни термин использовался во Франции для обозначения искусства вычислений в целом; возможно, также он использовал слово «логистический» в военном значении (управление резервами), подразумевая арифметическую стратегию (Pastijn, 2006).

В своей второй работе Ферхюльст иллюстрировал логистическую кривую, сравнивая ее с экспоненциальным (логарифмическим) ростом (рис. 1.10). В первой части логистической кривой нормальное население растет экспоненциально, только когда возделываются плодородные земли, а затем наступает замедление роста. Относительный темп роста сокращается с ростом населения, точка перегиба (в которой темп роста достигает своего максимума) всегда находится на полпути от верхнего предела, и в конце концов избыточное население достигает своего максимума. Моментальный темп роста логистической функции (ее производной относительно времени) распределяется нормально, достигая пикового значения в точке перегиба кривой (рис. 1.11). Более высокие темпы роста дадут более крутые кривые роста, достигающие максимального значения быстрее (кривая будет ограничена горизонтально), в то время как более низкие темпы роста дадут кривые, вытянутые по горизонтали.

В своей работе 1845 года Ферхюльст утверждал, что увеличение дальнейшего роста населения будет пропорционально размеру избыточного населения (population surabondante), и когда он использовал функцию роста для определения пределов размера населения Бельгии и Франции, то установил отметки на уровне 6,6 млн и 40 млн соответственно, которые будут достигнуты до конца XX века. Но в своей последней работе на тему роста населения он пришел к выводу, что препятствия к росту населения пропорциональны отношению между избыточным населением и общим населением (Verhulst, 1847). Это изменение дало более высокое значение конечного населения, или, как позже стали называть его асимптотическое значение, более высокий показатель предельной нагрузки (Schtickzelle, 1981).

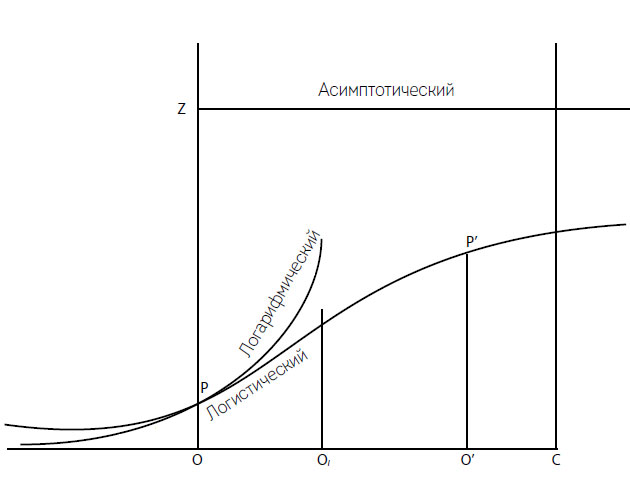
Рис. 1.10. Сравнение логистической и логарифмической (экспоненциальной) кривых Ферхюльста (1845)

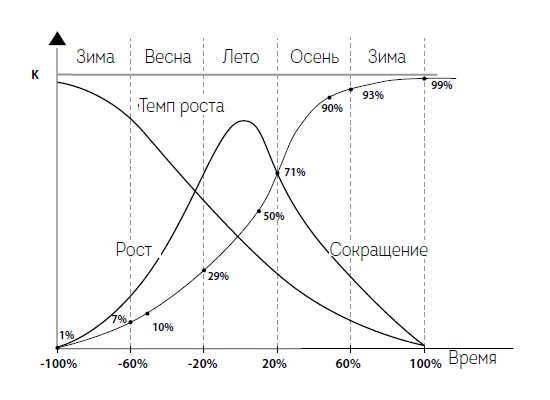
Рис. 1.11. Качественные характеристики логистического роста

По сути, уравнение Ферхюльста отражает смену доминирования (или, математически говоря – мажорирования) между двумя циклами обратной связи: цикл позитивной обратной связи (FBL) инициирует рост, который в конце концов замедляется и уравновешивается негативной обратной связью, отражающей пределы роста, преобладающие в ограниченном мире. Как выразился Кунш (Kunsch, 2006, 35), логистический рост «описывается как сочетание экспоненциального роста, выраженного в (+) FBL, и целенаправленного роста, выраженного в (—) FBL». В этом смысле функцию Ферхюльста с двумя циклами обратной связи, конкурирующими за доминирование, можно рассматривать как основу динамики систем, базирующихся на обратной связи, разработанную Джеем Форрестером из Массачусетского технологического института в 1950-е и 1960-е годы (Forrester, 1971) и примененную в исследовании под названием «Пределы роста», поддержанном Римским клубом (Meadows et al., 1972).

Эта ключевая систематическая концепция ограниченного роста (высокая плотность организмов является непосредственным сдерживающим фактором, а доступность ресурсов – сложной причинной движущей силой) полезна при концептуализации многих природных, социальных и экономических достижений, включая серии обратной связи, но ее механическое применение может вызывать серьезные ошибки. Оригинальные прогнозы роста населения, сделанные Ферхюльстом, представляют собой первые примеры таких ошибок, так как максимальные значения населения не предопределяются какой-либо конкретной функцией роста, а зависят от изменения производственного потенциала страны и в конечном счете всей планеты с помощью научного, технического и экономического прогресса. Сколько можно поддерживать эти максимальные значения на высоком, развивающемся уровне – другой вопрос. Ферхюльст в конце концов увеличил прогнозируемый размер населения Бельгии к 2000 году с 6,6 млн до 9,5 млн человек, но к концу XX века население Бельгии и Франции составляло 10,25 млн и 60,91 млн человек соответственно, то есть для Бельгии было приблизительно на 8 % выше скорректированного Ферхюльстом максимума, а для Франции ошибка составляла 52 %.

Во второй половине XIX века наблюдался всплеск демографических и экономических исследований, однако работу Ферхюльста игнорировали, и она была обнаружена только в 1920-е годы, а влияние приобрела в 1960-х годах (Cramer, 2003; Kint et al., 2006; Bacaër, 2011). Это не единственной пример подобного забвения: фундаментальные эксперименты Грегора Менделя в области генетики растений, проводившиеся в 1860-х годах, также игнорировались в течение почти полувека (Henig, 2001). Можно ли объяснить пренебрежение работами Ферхюльста сомнениями Кетле в ценности вклада его учеников, высказанными в надгробной речи, посвященной преждевременной смерти Ферхюльста в 1849 году? Удни Юл предлагает более правдоподобное объяснение: «Вероятно, в силу того, что Ферхюльст значительно опередил свое время и что существовавшие тогда данные не подходили для того, чтобы эффективно проверить его взгляды, они были преданы забвению, но остаются классикой в этой области» (Yule, 1925a, 4).

Следующее появление логистической функции (без использования этого названия) было связано с количественным выражением прогресса аутокаталитических реакций в химии. Если катализ обозначает повышающуюся скорость химической реакции, что вызвано присутствием дополнительного элемента (в частности, какого-либо тяжелого металла) или сложного вещества (часто в ничтожных количествах), то аутокатализ означает реакцию, ускоряющуюся за счет собственных результатов. Аутокаталитические процессы – реакции, демонстрирующие ускорение темпов роста как функцию от времени, за которым следует насыщение, – необходимы для роста и поддержания живых систем, и без них абиотические химические факторы не смогли бы привести к репродукции, обмену веществ и эволюции (Plasson et al., 2011; Virgo et al., 2014).

После того как Вильгельм Оствальд (1853–1932, ведущий химик времен до Первой мировой войны) представил данную концепцию в 1890 году (Ostwald, 1890), стало быстро понятно, что процесс развивается в соответствии с логистической функцией: концентрация одного реагента повышается по сравнению с начальным уровнем, сначала медленно, потом быстрее, но затем, с учетом ограниченного количества другого реагента, процесс замедляется, а концентрация второго реагента постепенно уменьшается до нуля. В 1908 году Брейлсфорд Робертсон (1884–1930), австралийский физиолог из Калифорнийского университета, отметил, что, если сравнить кривую мономолекулярной аутокаталитической реакции с кривой роста массы тела самцов белых крыс, «схожесть между кривой роста и кривой аутокаталитической реакции сразу становится очевидной» (рис. 1.12) – но сравнение кривой аутокаталитической мономолекулярной реакции с кривой роста массы тела мужчины показало, что вторая из этих траекторий имеет две совмещенные кривые (Robertson, 1908, 586).

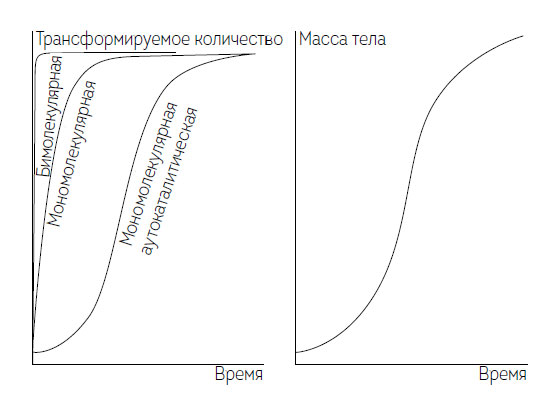
Рис 1.12. Сравнение Робертсоном (Robertson, 1908) прогресса аутокаталитической реакции и увеличения массы тела самцов белой крысы

Обе кривые являются сигмоидальными, но Робертсон не упомянул Ферхюльста. Три года спустя Маккендрик и Кесава Паи (McKendrick and Kesava Pai, 1911) использовали эту функцию, снова не называя имени Ферхюльста, для изображения роста микроорганизмов, а в 1919 году Рид и Холланд (Reed and Holland, 1919) сослались на Робертсона (Robertson, 1908), но не использовали термин «логистическая» в своей кривой роста подсолнечника. Этот пример роста растений позже стал широко цитироваться в биологической литературе, посвященной теме роста.

Наблюдаемый рост в высоту подсолнечника (Helianthus) в период между посадкой и 84-м днем очень близко соответствует логистической функции с четырьмя параметрами, где точка перегиба приходится на 37-й день (рис. 1.13).

В 1920 году логистическая функция снова появилась в демографии, когда Реймонд Перл и Лоуэлл Рид, профессора Университета Джонса Хопкинса, опубликовали работу, посвященную росту населения США (Pearl and Reed, 1920), но только два года спустя они кратко признали первенство Ферхюльста (Pearl and Reed, 1922). Во многом как и Ферхюльст в середине 1840-х годов, Перл и Рид использовали логистическую функцию, чтобы вычислить максимальный размер населения США, который сможет прокормить сельское хозяйство страны (Pearl and Reed, 1920, 285):

Верхняя асимптота… имеет значение приблизительно 197 274 000. Это означает, что… максимальное население, которое будут иметь континентальные США при текущем ограничении площади, будет приблизительно вдвое выше нынешнего. Мы боимся, что некоторые осудят всю теорию, потому что это число недостаточно внушительно. Рассчитать население с помощью геометрической прогрессии (и большинство авторов работ на тему населения склоняются к этому) или с помощью параболы или другой чисто эмпирической кривой и прийти к таким изумляющим цифрам настолько легко, что спокойно осмыслить реальную вероятность этого будет крайне сложно.

Рис. 1.13. Логистический рост (точка перегиба на 37,1-й день, асимптота на уровне 292,9 см) растения подсолнечника, изображенный Ридом и Холландом (Reed and Holland, 1919)

Как в случае с максимальными цифрами населения Ферхюльста для Бельгии и Франции, Перл и Рид также недооценили приемлемый максимум населения США. К 2018 году оно превысило 325 млн, что почти на 65 % больше их расчетов максимальной предельной нагрузки (рис. 1.14) – даже с учетом того, что 40 % урожая кукурузы, крупнейшей сельскохозяйственной культуры США, перерабатывают в этиловый спирт и страна является крупнейшим в мире экспортером продуктов питания. Но Перл не сомневался в прогностической силе своего уравнения: в 1924 году он «скромно» сравнил кривую с законом движения планет Кеплера и законом о газах Бойля (Pearl, 1924, 585).

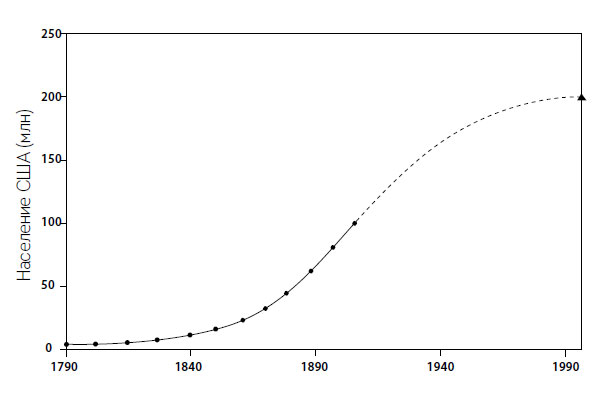
Рис. 1.14. Прогноз роста населения США на основе логистической кривой (точка перегиба в 1919 году, асимптота на уровне 197,3 млн), согласованный с переписью населения, проводившейся раз в десять лет в период между 1790 и 1910 годами (Pearl and Reed, 1920)

Применение функции логистического роста начало распространяться. Робертсон использовал информацию о росте молочных коров, домашней птицы, лягушек, однолетних растений и фруктовых деревьев в своем объемном исследовании под названием The Chemical Basis of Growth and Senescence («Химические основы роста и старения») (Robertson, 1923). Год спустя Спиллман и Ланг (Spillman and Lang, 1924) подробно изложили Закон убывающего плодородия, приведя множество количественных описаний ограниченных темпов роста. Рид и Берксон (Reed and Berkson, 1929) применили логистическую функцию к нескольким бимолекулярным реакциям и протеолизу гелеобразования с помощью панкреатина, а Блисс (Bliss, 1935) использовал ее для расчета кривой зависимости смертности вредителей от дозировки пестицидов. И в течение двадцати лет до Второй мировой войны Перл и его коллеги применяли логистическую кривую «к популяциям почти всех живых существ от плодовых мушек до населения французских колоний в Северной Африке, а также росту дынь канталуп» (Cramer, 2003, 6).

В 1945 году Харт опубликовал всестороннее исследование логистических социальных тенденций со множеством примеров, поделенных на серии, отражающие рост конкретных социальных единиц (населения, городов, урожая, производства и потребления промышленных продуктов, выдачи патентов на изобретения, длины железных дорог), распространение конкретных культурных явлений (охват детей школьным образованием, владение автомобилями, социальные и гражданские движения) и так называемые индексы социальной эффективности, включая продолжительность жизни, рекорды скорости и доход на душу населения (Hart, 1945). В течение двадцати лет после окончания Второй мировой войны наблюдался быстрый рост населения и экономический рост, вызванный расширением технических возможностей. В тот период преобладали многочисленные примеры экспоненциального роста, но с ростом экологического сознания в конце 1960-х и 1970-х логистическая функция снова получила популярность. Неудивительно, что существует множество публикаций о том, как описать данные с помощью логистической кривой (Cavallini, 1993; Meyer et al., 1999; Arnold, 2002; Kahm et al., 2010; Conder, 2016).

Существует еще одна довольно распространенная модель роста – кривая Гомпертца, выведенная еще раньше функции Ферхюльста. Изначально модель была предложена в 1825 году Бенджамином Гомпертцем (1779–1865), британским математиком, для оценки смертности людей (Gompertz, 1825). В ней, как и в логистической функции, имеются три константы, асимптота и фиксированная степень асимметрии, но, как уже отмечалось, логистическая функция имеет точку перегиба точно посередине между двумя асимптотами, и ее кривая радиально симметрична по отношению к этой точке перегиба. В отличие от нее функция Гомпертца дает асимметричную кривую с точкой перегиба на уровне 36,78 (е–1) асимптотического максимума и, следовательно, асимметрична (Tjørve and Tjørve, 2017). Эта кривая подходит лучше, чем логистическая, для моделирования процессов сигмоидального роста, которые замедляются после достижения приблизительно трети от своего максимального значения (Vieira and Hoffmann, 1977).

Более века спустя Винзор (Winsor, 1932, 1) отмечал, что «кривая Гомпертца долго интересовала только статистиков страховых учреждений. Однако в последнее время она используется различными авторами как кривая роста для оценки как биологических, так и экономических феноменов». Но он называл только три области применения: рост веса скота (но только после того как животные достигли около 70 % своей зрелой массы), рост размера раковины двустворчатого моллюска и рост гигантского Тихоокеанского моллюска, – делая вывод, что в силу практически аналогичных свойств ни логистическая кривая, ни кривая Гомпертца не имеют «значительного преимущества друг перед другом в отношении количества явлений, рост которых можно было бы описать с их помощью» (Winsor, 1932, 7).

Но это было до того, как во многих исследованиях было обнаружено, что более старая функция во многих случаях является предпочтительной. К природным явлениям, которые лучше всего описывает функция Гомпертца, относятся такие фундаментальные биохимические процессы, как рост нормальных и злокачественных клеток, кинетика ферментативных реакций и интенсивность фотосинтеза как функция концентрации CO2 в атмосфере (Waliszewski and Konarski, 2005). Когда логистическое уравнение стало чаще использоваться для изучения роста организмов, многие исследователи отмечали ограничения функции при воспроизведении наблюдаемого роста животных и растений и ее недостаточную надежность при прогнозировании прироста на основе прошлых показателей. Нгуимке (Nguimkeu, 2014) предлагает простой дифференциальный тест для выбора между моделями Гомпертца и логистического роста.

Основным недостатком кривой логистического роста является ее симметрия: она напоминает колебания маятника, набирающего максимальную скорость в середине траектории. Точка перегиба логистической кривой приходится на 50 % максимального значения, в результате чего схема роста дает симметричную колоколообразную кривую (кривую Гаусса), которая будет рассмотрена в следующем разделе. Многие организмы демонстрируют более быстрые темпы роста на начальных стадиях, и кривые их роста достигают точки перегиба гораздо раньше, чем асимптотического максимума. Аналогично многие процессы распространения (будь то внедрение новых промышленных методов или распространение владения бытовой техникой) следуют асимметричной S-образной траектории.

И поскольку степень асимметрии также зафиксирована в асимметрической функции Гомпертца, многие попытки избавиться от этих недостатков ведут к формулированию нескольких дополнительных моделей роста логистического типа. Цуларис (Tsoularis, 2001) рассмотрел эти производные модели – главные из которых были представлены Берталанффи (von Bertalanffy, 1938), Ричардсом (Richards, 1959), Блумбергом (Blumberg, 1968), Тернером и др. (Turner et al., 1976) и Берчем (Birch, 1999), – а также предложил собственную обобщенную логистическую функцию, из которой можно получить все эти модификации. Они не систематизированы в зависимости от практической ценности: все эти функции принадлежат к одной семье (являясь вариациями на тему S-образного роста), и ни одна из них не превосходит другие сигмоидальные кривые с тремя постоянными по степени пригодности.

Фон Берталанффи (von Bertalanffy, 1938) построил уравнение роста на аллометрическом (неравномерном) соотношении между скоростью обмена веществ и массой тела животного, где масса меняется в связи с разницей анаболических и катаболических процессов. Максимальный темп роста функции (точка перегиба) находится на уровне около 30 % (8/27) асимптотического значения и применяется при изучении роста и продукции лесного хозяйства, но особенно в гидробиологии, для коммерческих видов рыбы, таких как треска (Shackell et al., 1997), тунец (Hampton, 1991), а также акул (Cailliet et al., 2006) и даже белых медведей (Kingsley, 1979). Однако Рофф (Roff, 1980, 127) доказывал, что данная функция «в лучшем случае пригодна для отдельных случаев, а в худшем – лишена смысла» и от нее следует отказаться, так как она исчерпала себя в исследованиях рыболовного промысла. Дей и Тейлор (Day and Taylor, 1997) также пришли к выводу, что уравнение фон Берталанффи не следует использовать для моделирования возраста и размера организмов в период зрелости.

Ричардс (Richards, 1959) модифицировал уравнение фон Берталанффи, чтобы оно соответствовало эмпирическим данным о росте растений. Функция, также известная как модель роста Чапмана – Ричардса, имеет на один параметр больше, чем логистическая кривая (необходимый для асимметрии), и широко используется в исследованиях лесного хозяйства, а также для моделирования роста млекопитающих и птиц и для сравнения влияния ухода на рост растений, но имеются и возражения против ее использования (Birch, 1999). Ее точка перегиба колеблется на уровне от менее 40 % до почти 50 % асимптотического значения. Тернер и др. (Turner et al., 1976) называл модифицированное ими уравнение Ферхюльста универсальной функцией роста. Гиперлогистическая функция Блумберга (Blumberg, 1968) также является модификацией уравнения Ферхюльста, предназначенной для моделирования роста размеров органов, а также динамики населения.

И распределение Вейбулла, изначально разработанное для изучения вероятности отказа вследствие изменения свойств материала (Weibull, 1951) и используемое в тестах на надежность в инжиниринге, легко модифицируется для получения гибкой функции роста, которая может дать самые разнообразные сигмоидальные функции роста. Оно используется в лесном хозяйстве для моделирования высоты и объемного прироста отдельных видов деревьев, а также объема и возраста полиморфических лесных насаждений (Yang et al., 1978; Buan and Wang, 1995; Gómez-García et al., 2013). Двумя последними пополнениями по-прежнему растущего семейства сигмоидальных кривых являются новое уравнение роста, разработанное Берчем (Birch, 1999), и уже упоминавшаяся обобщенная логистическая функция Цулариса (Tsoularis, 2001). Берч модифицировал уравнение Ричардса, чтобы оно лучше подходило для универсальных имитационных моделей, особенно для представления роста различных видов растений с отличающимися вегетационными периодами, тогда как Цуларис (Tsoularis, 2001) предложил уравнение обобщенного логистического роста, включающее все прежде использовавшиеся функции в качестве особых случаев.