
Природа и свойства физического времени
Необходимо отметить также, что мы рассматриваем здесь элементарные случаи вычисления временного интервала. В более сложных случаях, когда в одном и том же процессе происходит одновременное множественное преобразование вложенной энергии, выражение для него может содержать сумму элементарных процессов и состоять из нескольких отношений обобщенных моментов инерции к соответствующим им элементам вложенной энергии.
Проверим полученную зависимость на правильность с точки зрения соответствия размерностей в системе СИ, ради простоты выполнив эту процедуру для квадрата интервала времени:

Как видно, соответствие размерностей в полученном выражении не нарушено, значит, это и есть искомая зависимость, характеризующая свойства физического времени.
Для того чтобы дополнительно убедиться, что полученное выражение имеет всеобъемлющий характер, возьмем случай, далекий от рассматриваемой тематики, например, время расползания волнового пакета частицы массы m0:
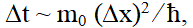
где m0 – масса частицы;
ħ – постоянная Планка.
Умножим обе стороны соотношения на
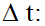
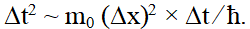
И, учитывая, что
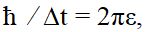

где ε – энергия частицы.
Откуда легко увидеть, что и в этом случае мы получаем то же выражение:

Из рассмотренных случаев видно, что, как мы и предполагали, из любой задачи динамики всегда получается одно и то же выражение для текущего временного интервала. Связано это с тем, что время как физическая величина имеет единообразный внутренний физический смысл для всей классической механики и, предположительно, и для всей физики вообще, несмотря на то, что первоначально оно было введено как не имеющая дополнительных свойств абстрактная длительность.
Прежде чем приступить к анализу найденной закономерности, необходимо сделать некоторые замечания о степени ее значимости и границах ее применимости.
В качестве исходной точки для последующих преобразований был взят второй закон Ньютона в каноническом виде. Поскольку этот закон выражает наиболее фундаментальные свойства материального мира, заключающиеся, во-первых, в существовании массы как меры инертности тела и, во-вторых, в способности этого тела изменять свою скорость под действием приложенной силы, то полученное выражение для величины интервала физического времени также является фундаментальным законом, связывающим меру противодействия со стороны материального тела изменению его энергии с количеством внешней энергии, вложенной в процесс движения, а следствия, из него вытекающие, имеют столь же фундаментальное значение.
Кроме того, выражение для временного интервала было получено из второго закона без каких-либо специальных ограничений или искусственных приемов, выходящих за рамки классической механики. Поэтому полученное выражение может быть применено в той же мере и тех же случаях, что и упомянутый выше закон. То есть выражение для временного интервала, полученное подобным образом, без каких-либо ограничений применимо в границах применимости классической механики.
И отсюда следует главный вывод: если считать, что второй закон Ньютона адекватно описывает реальные движения, то полученное выражение описывает их столь же адекватно.
При этом учитывается, как уже ранее отмечалось, некоторая ограниченность описания, присущая абстрактному изображению реального движения.
Отмечая это, приходим к окончательному выводу, что выражение вида
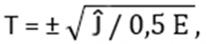
где Т – временной интервал;
Ĵ – обобщенный момент инерции;
E – вкладываемая в процесс или извлекаемая из процесса сторонняя энергия, имеет для классической механики всеобщий характер и исчерпывающим образом характеризует физическое время, фигурирующее в ее задачах.
Перейдем теперь к анализу свойств выведенной закономерности.
Заметим, прежде всего, что величина временного интервала, выраженная таким образом, может быть вычислена для реального, наблюдаемого в действительности движения действительно существующего материального тела. Несмотря на то, что мы вначале исходили из представления об абсолютном времени, которое постулируется для применения в законах Ньютона, полученное из анализа этих законов время (поскольку, как мы считаем, они адекватно описывают реальность) уже имеет иные характеристики. То, что свойства времени, выражение для которого было получено подобным образом, отличаются от свойств Ньютонова абсолютного времени, мы покажем, когда подробно проанализируем эти свойства, но даже без подробного анализа видно, что эти свойства скорее соответствуют тому относительному времени, которое Ньютон считал «кажущимся» и неспособным при его применении в научном исследовании адекватно описывать явления окружающего нас мира.
Отсюда следует, что Ньютон, давая характеристику абсолютному и относительному времени, описал ситуацию, противоречащую реальному положению дел. На самом деле всеобщим определением времени является то, что он объявляет относительным, а его абсолютное характеризует лишь некий ограниченный набор частных случаев, то есть представляет собой определение особенного.
Поэтому, чтобы отличать наше представление от представления Ньютона, мы будем далее везде называть отрезки времени в нашем представлении временным интервалом (с ударением на третьем слоге первого слова). И, говоря о временном интервале, нужно учитывать, что на самом деле мы обсуждаем свойства того реального физического времени, о котором шла речь в начале исследования.
Первое, что бросается в глаза при рассмотрении выражения для временного интервала, – это полное и окончательное устранение из проблемы физического времени любых, даже самых слабых, намеков на существование у времени каких-либо мистических свойств.
Время в классической механике является параметром, принципиально не выделяющимся среди других общепринятых параметров, таких как, например, сила, масса, скорость, ускорение и т. д., и это обстоятельство позволяет раз и навсегда отмежеваться от многочисленных попыток спекулятивного использования его свойств в разного рода эзотерических конструкциях.
Вторым выводом, непосредственно следующим из самого вида закономерности, является утверждение о том, что время не является самостоятельной материальной сущностью. В отличие от абсолютного времени Ньютона квазиматериальность не является необходимым свойством временного интервала ни теоретически, ни при практическом его использовании в реальных динамических задачах. Квадрат значения временного интервала в построениях классической механики есть счетная величина, как и считал в свое время Аристотель. Она в итоге есть отношение сопротивления протеканию процесса к половине энергии, вкладываемой в процесс или извлекаемой из него. Поэтому время по своей сути есть отношение. Однако, будучи отношением, оно, тем не менее не имеет материального воплощения, как, например, масса. У времени в нашей интерпретации нет такой двойственности: время, используемое в физических зависимостях, есть число, и у него нет присущих Ньютоновому времени противоречивых свойств.
Физически время есть измеренная продолжительность единичного процесса и вне процесса не существует.
Являясь абстрактной характеристикой реального материального взаимодействия, его параметром, свойством, присущим движению материи, т. е. свойством свойства или свойством в квадрате, само время, поэтому особым видом материи, как, например, электромагнитное поле, не является, и непосредственно с ним невозможно производить материальные преобразования. Подобные действия можно предпринять лишь по отношению к самому движению, воздействуя на условия его осуществления. И лишь в результате этого параметры движения, в том числе и время, изменятся в свою очередь. Поэтому время само по себе, независимо от движения, к которому оно относится, нельзя как нечто самостоятельно существующее «отразить», «сжать», «повернуть», извлечь из него энергию, как нельзя извлечь, например, энергию из числового значения скорости или ускорения, поскольку «движет» процесс не время, а вложенная в процесс сторонняя энергия.
Подобное заключение, объявляющее ложной субстанциональную концепцию, которой придерживался Козырев, требует дополнительного пояснения. Для того чтобы сделать такое заявление, нам пришлось использовать полученное ранее общеизвестное математическое выражение, связывающее между собой некоторые физические величины (второй закон Ньютона), и в результате анализа этого выражения определить свойства временного интервала. Подобный способ объяснения физических явлений широко применяется в современной науке и не является чем-то необычным или недостаточно строгим. Собственно, вся математическая физика построена на этом приеме. Вопрос здесь заключается лишь в том, какое математическое выражение при этом берется за основу, насколько оно соответствует и как точно описывает истинные закономерности реального мира?
Но мы уже указывали, что выражение для временного интервала, выведенное из второго закона Ньютона, является столь же фундаментальным, как и этот закон. А поскольку второй закон Ньютона появился в результате обобщения и осмысления гигантского количества опытных данных, взятых из наблюдений над природными явлениями, то можно считать, что и прямые следствия из этого закона в той же степени соответствуют природным явлениям. То есть выражение для временного интервала можно также считать полученным, в конечном счете, из обобщения опытных данных, взятых из наблюдений над природными явлениями. В то же время субстанциональная концепция Козырева получена из анализа математического выражения, которому, как мы впоследствии покажем, вообще не соответствует никакая физическая реальность. Это обстоятельство позволяет нам полностью проигнорировать физический смысл и сущность положений теории времени, предложенной Козыревым, не тратя усилий, за некоторыми исключениями, на детальное обсуждение этих положений. Коротко можно лишь заметить, что «зеркала времени», заявленные Козыревым, невозможны по вышеописанным обстоятельствам, а в его экспериментах присутствуют невыясненные доселе артефакты, либо не относящиеся к времени непосредственно необъясненные эффекты.
Третьим выводом относительно природы времени, вытекающим из вида полученной зависимости, будет категорическое утверждение о его строгой локальности в виде временного интервала.
Никакого единого всеобщего времени, «текущего» через весь материальный мир и «движущего» собой все процессы Вселенной, принципиально не существует. Или, по-другому, никакого иного времени, кроме того, что мы называем физическим, представляющим собой продолжительность единичного процесса, не существует в реальности. Всякого рода «духовные», «внутренние», «субъективные», «личностные», «векторные», «линейные», «статические», «динамические», «субстанциональные», «реляционные» и прочие виды времени есть отражение в сознании человека различных сторон реального физического времени как измеренной продолжительности единичного процесса.
Если хотя бы для одного процесса можно найти временному интервалу иное объяснение, чем Ньютонова концепция, вся она полностью должна быть пересмотрена, так как всеобщее абсолютное время может существовать только в согласии с принципом «все, или ничего». Поскольку оно принято неизменным и независимым, то любой намек на другие свойства, тем более на зависимость и изменяемость, разрушает саму основу этой концепции. Но мы получили вполне определенное выражение для временного интервала простейшего случая – механического движения, которое строится принципиально противоположно абсолютному времени. Время в нашем случае является функцией вложенной энергии и сопротивления внутри процесса происходящим под действием этой энергии изменениям. Поэтому приходим к неизбежному выводу, что единственным материальным носителем реально существующего времени как свойства движения является сам единичный процесс, длительность протекания которого или его части и выражает величина временного интервала.
Времени, существующего самостоятельно, отдельно от единичного процесса, в реальности не бывает. Время всегда конкретно, т. е. всегда принадлежит конкретному процессу. И это правило не знает исключений.
А это означает, что время есть только там, где есть процесс, есть движение материи. Если такого движения не наблюдается, то никакого времени в этом случае нет. Его не существует. Соответственно, всегда, когда мы имеем счет времени, он производится неким процессом, либо уже существующим, либо специально организованным. Поэтому время вообще, существующее самостоятельно, а именно «единое всеобщее независимое время», есть абстракция, присутствующая только в нашем сознании.
Как ни странно, Ньютон, вводя свое абсолютное время в обиход научного исследования, хорошо это понимал. Он не интересовался свойствами относительного времени и не рассматривал возможности его применения в законах движения, считая его изменчивым, а потому и недостоверным, но, тем не менее, признавал его существование. Его оговорка по поводу того, что «относительное время есть мера продолжительности, совершаемая при посредстве какого-либо движения», прекрасно это демонстрирует. И когда, в соответствии с ранее заданным вопросом, мы переходим от его абсолютного времени к его же относительному, то обнаруживаем, что материальным, ощутимым и здесь является только наблюдаемый нами процесс, то есть движение, о котором говорил Ньютон. Наблюдаемое же в реальности время служит лишь характеристикой этого движения, то есть само по себе ни в коем случае не является материальной сущностью. Этим заявлением полностью устраняется та противоречивость, которая присуща абсолютному времени Ньютона. Отсюда, в свою очередь, следует заключение, что единое всеобщее время, которое мы себе представляем и в которое, как нам кажется, мы «погружены», на самом деле есть результат сложения длительностей бесчисленных отдельных процессов в единое существование Вселенной, Земли и человечества. «Река времени» как поэтический образ также существует только в нашем сознании и лишь отражает в нем совместное существование этого бесконечного числа отдельных процессов.
Оставляя пока в стороне вопрос о мнимом времени, которое в классической механике не рассматривается, заметим, что, поскольку подкоренное выражение в зависимости для временного интервала сугубо положительно, значения временного интервала действительны во всей области их существования. Что это именно так, можно убедиться непосредственно. Масса в классической механике не может быть отрицательной. Длина пройденного телом пути входит в выражение для обобщенного момента инерции во второй степени, поэтому направление движения в первом приближении не играет роли при определении длительности. И хотя энергия в равной степени может вкладываться в процесс (при разгоне тела, например) и извлекаться из него (при торможении), сама по себе она, в границах применимости второго закона, всегда имеет действительное, также сугубо положительное, значение. Но при положительном подкоренном выражении временной интервал представляет собой, как уже указывалось, действительное число или функцию действительного переменного. Эта функция имеет в общем случае двузначный вид, так как квадратный корень в нашей зависимости мы вынуждены принимать и со знаком плюс, и со знаком минус, поскольку не существует никаких специальных соображений, которые запрещали бы нам использовать оба знака в полученном выражении. Кроме того, двойной знак в выведенной формуле появляется исключительно из-за того, что время входит во второй закон Ньютона в составе второй производной. А это обусловлено только свойствами нашего физического мира, и ничем иным. Если бы время в этом законе входило в состав первой производной, то двойной знак перед отношением обобщенного момента инерции к энергии отсутствовал бы, что легко проверить. Поэтому мы не можем из соображений здравого физического смысла, как это обычно бывает, проигнорировать знак минус перед корнем в формуле для величины временного интервала. А необходимость использования обоих знаков приводит нас еще к одному выводу.
Четвертым, неожиданным и важнейшим выводом, имеющим далекоидущие последствия для физической теории, является утверждение, что в нашей Вселенной, понимаемой как объективная реальность в самом широком смысле, при известном наборе мировых констант, совместно существуют два равноправных встречных направления протекания механических процессов во времени. Эти процессы могут быть полностью идентичны, их временные интервалы могут иметь равное значение, но последовательности смены этапов у них будут направлены навстречу друг другу. Или по-другому в нашей Вселенной существуют два равноправных, но встречно-направленных способа возрастания энтропии.
Заметим по этому поводу, что исходное выражение для временного интервала, как мы уже отмечали, адекватно описывает реальную физическую действительность. Поэтому оба знака времени не являются следствием особенностей математических операций при выведении зависимости, а соответствуют реальному положению вещей в окружающем нас материальном мире. Иными словами, причиной появления многозначности у выражения для временного интервала являются особенности строения Вселенной, а сама многозначность есть лишь следствие описания этих особенностей, а не наоборот.
Возвращаясь к предпосылкам нашего вывода, можно сказать, что второй закон Ньютона сформулирован таким образом, что не является Т – инвариантным в строгом смысле слова, а объединяет в абстракции две идентичные, но противоположно направленные во времени независимые ветви процессов, существующие в реальности.
Иными словами, в природе совместно существуют два направления времени: из нашего прошлого в наше будущее и из нашего будущего в наше прошлое.
Если распространить понятие временного интервала в нашем понимании (как отношение сил сопротивления изменениям к вложенной энергии) на все возможные процессы, то получится, что именно потому и многие другие законы, использующиеся в физике, выглядят Т-инвариантными, поскольку большинство из них сформулированы таким образом, что в своей формулировке описывают все явление, состоящее из одномоментно существующих, противоположно направленных временных ветвей, а поэтому не различают противоположных временных направлений. Этим же утверждением разрешается также проблема «запаздывающих» и «опережающих» потенциалов, соответствующие уравнения которых описывают разные направления времени в нашем мире. То есть опережающие потенциалы описывают процессы в минус-времени, которые наблюдались бы в нашем мире, если бы происходили на наших глазах. При этом запаздывающие потенциалы описывают реально существующие процессы, которые принадлежат нашему плюс-времени.
Удивительно, что Ньютон, формулируя свое определение абсолютного времени, однозначно указывал на его движение («протекает»), но никоим образом не определял направление или направления этого «протекания», в противоположность позднейшим исследователям, что свидетельствует не только о его научной добросовестности, но и о его безошибочной интуиции.
Итак, непосредственный и предварительный анализ зависимости для временного интервала позволяет сделать следующие исходные и неоспоримые заключения:
1. Время в классической механике является параметром, принципиально не выделяющимся среди других общепринятых параметров, таких как, например, сила, масса, скорость, ускорение и т. д.
2. Время представляет собой свойство движения материи, а не ее форму.
3. Время не является самостоятельной материальной сущностью.
4. Единого всеобщего времени, «пронизывающего» все процессы Вселенной, не существует.
5. Временной интервал строго локален. Любая реальная длительность (длительность реального процесса) слагается из бесчисленного количества длительностей элементарных актов движения, составляющих этот процесс.
6. Во Вселенной, при известном наборе мировых констант, совместно существуют два равноправных встречных направления протекания механических процессов во времени.
3. Темп времени
Для абсолютного времени, представляемого как течение реки, совершенно естественным выглядит существование некоего «хода» времени – равномерного и непрерывного одностороннего движения из нашего прошлого в наше будущее. Именно это движение, по существующим представлениям, «несет» все процессы и все тела в одну сторону. На него мы, по представлениям Ньютона, повлиять не в силах, и нам остается только наблюдать, какие изменения в окружающем мире, «уносимом» в неизвестное будущее, происходят на наших глазах. Главная особенность такого движения, введенная аксиоматически, – это неизменность скорости. Абсолютное время всегда и во всех случаях «движется» с постоянной скоростью, не изменяющейся ни при каких условиях.
Если мы переходим к использованию временного интервала, то подобное свойство уже не может приниматься нами в качестве основного для времени, как мы и покажем в дальнейшем. Однако, рассматривая выражение для временного интервала и подчеркивая, что время есть число, мы, таким образом, фиксируем продолжительность завершившейся части процесса. Но временной интервал есть результат движения процесса от начала к концу и, следовательно, результат его динамических свойств. Когда мы фиксируем результат, свойства временного интервала в промежутке между началом и концом движения остаются в тени. Между тем в зависимости от конкретного значения выведенного ранее соотношения: сопротивление развитию процесса – вложенная в процесс энергия; скорость его развития может меняться не только для разных процессов, но даже и внутри одного и того же временного интервала.
И для того чтобы было возможно сравнивать между собой процессы одного и того же вида, но происходящие при разных условиях, необходимо ввести скорость изменения величины временного интервала по отношению к одной из величин, входящих в выражение для него и являющихся по отношению к нему аргументом. Наиболее универсальной в этом смысле является величина вложенной в процесс энергии. Поэтому для характеристики процесса введем производную от времени по величине вложенной энергии и назовем ее темпом времени:
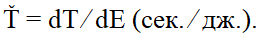
Темп времени – достаточно устоявшееся в темпорологии понятие. Оно определяет частоту событий в течение некоего определенного промежутка времени, что в элементарном виде представляет собой расстояние во времени от одного события до другого, т. е. внешний по отношению к процессу счет. Введенный же нами темп, напротив, характеризует процесс с точки зрения внутренних свойств временного интервала. Внешний счет времени, который также может здесь использоваться, относится в рассматриваемом случае исключительно к изменениям в процессе, происходящим внутри временного интервала, и не распространяется на события, происходящие за пределами этого интервала. Темп времени в нашей интерпретации – это характеристика движения в интервале от

Введение темпа времени позволяет, во-первых, сравнивать между собой процессы одного вида по скорости их протекания и, во-вторых, различать между собой этапы процесса, протекающие в изменившихся по отношению к энергии условиях.
Если
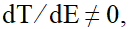
Темп времени, введенный подобным образом, не является еще одним его (времени) измерением, так же как скорость движения не является дополнительным измерением пространства. Хотя это утверждение само по себе является физической банальностью, забвение смысла этого обстоятельства встречается не так редко, как хотелось бы. Попытки сконструировать многомерное время, приспосабливая в виде дополнительных измерений его искусственные характеристики, существуют, и игнорировать их существование было бы безответственно.