
Закат Западного мира. Очерки морфологии мировой истории
Диофант жил ок. 250 г. по Р. X., т. е. в третьем столетии арабской культуры, чей исторический организм лежал до сих пор погребенным под поверхностными формами римской императорской эпохи и «Средневековья»[52], между тем как к ней относится все то, что возникло посреди ландшафта будущего ислама. Именно тогда перед лицом нового пространственного ощущения купольных строений, мозаик и рельефов саркофагов в древнехристианско-сирийском стиле изгладились последние следы пластики античной статуи. Тогда снова появились архаическое искусство и строго геометрический орнамент. Именно тогда Диоклетиан довел до конца создание халифата теперь уже только по наружности Римской империи. 500 лет отделяют Диофанта от Евклида, Плотина – от Платона, первого схоластика только пробудившейся тогда культуры Дунса Скота – от последнего, замыкающего мыслителя культуры завершенной, Канта.
Здесь мы впервые сталкиваемся с неведомым прежде существованием тех великих индивидуумов, чье становление, рост и увядание образуют подлинную субстанцию всемирной истории, протекающей под тысячеликой, приводящей в замешательство поверхностью. Пришедшая к своему завершению в римской интеллигенции античная душевность, чье «тело» образует античная культура с ее произведениями, идеями, деяниями и развалинами, появилась на свет ок. 1100 г. до Р. X. среди ландшафта Эгейского моря. Зарождающаяся на Востоке начиная с Августа под покровом античной цивилизации арабская культура берет свое начало всецело из недр ландшафта между Арменией и Южной Аравией, Александрией и Ктесифоном. В качестве выражения этой новой души следует рассматривать почти все «позднеантичное» искусство императорского времени, все пронизанные юным жаром восточные культы, мандаитскую и манихейскую религии, христианство и неоплатонизм, императорские форумы в Риме и возведенный там Пантеон, эту самую раннюю из всех мечетей.
То, что в Александрии и Антиохии писали все еще по-гречески и полагали также, что по-гречески мыслят, имеет не большее значение, чем то обстоятельство, что наука Запада вплоть до Канта предпочитала латинский язык или что Карл Великий «возродил» Римскую империю.
У Диофанта число больше не есть мера и сущность скульптурных вещей. На мозаиках Равенны человек более не тело. Греческие обозначения незаметно утратили свое первоначальное содержание. Мы покидаем область аттической καλοκἀγαθία [физического и нравственного совершенства (греч.)], стоических ἀθαραξία и γαλήνη [невозмутимости и безмятежности (греч.)]. Правда, Диофанту еще неизвестны нуль и отрицательные числа, однако скульптурные единицы пифагорейских чисел ему уже неизвестны. С другой стороны, неопределенность неименованных арабских чисел представляет собой все же нечто совершенно иное, нежели закономерная изменчивость позднего западного числа, функции.
Магическая математика вполне последовательно и мощно развивалась (хотя подробности этого нам неизвестны) и после Диофанта (который уже сам предполагает определенное развитие) вплоть до своего завершения в эпоху Аббасидов в IX в., как это доказывается уровнем знаний у Аль-Хорезми и Аль-Зиджи. Что означает рядом с евклидовой геометрией аттическая скульптура (тот же самый язык форм в ином обличье), что означает рядом с пространственным анализом полифонический стиль в инструментальной музыке, то же самое означает рядом с этой алгеброй магическое искусство мозаики, все с большим богатством развивавшиеся в империи Сасанидов, а позже в Византии арабески с их чувственно-бесплотным улетучиванием (Verschweben) органических формальных мотивов и горельефы константиновского стиля с неопределенной глубокой темнотой фона, оставленного между свободно изваянными фигурами. Как алгебра соотносится с античной арифметикой и западным анализом, так и купольная церковь соотносится с дорическим храмом и готическим собором.
Не то чтобы Диофант был великим математиком. То, из-за чего чаще всего вспоминают его имя, содержится не в его трактатах, а то, что в них содержится, вне всякого сомнения, не является всецело его собственностью. Его обязанное случаю значение заключается в том, что – насколько нам известно – у него первого с совершенной несомненностью заявило о себе новое ощущение числа. Сравнивая его с мастерами, завершавшими математику, такими как Аполлоний и Архимед в античной математике и соответствующие им Гаусс, Коши и Риман – в математике западной, мы находим у Диофанта, прежде всего в его формульном языке, нечто примитивное, что до сих пор охотно приписывалось позднеантичному упадку. Впоследствии мы это поймем и научимся ценить – по образцу той переоценки до сих пор прямо-таки презиравшегося якобы позднеантичного искусства в продвигающееся пока на ощупь самовыражение только еще пробуждающегося раннеарабского мироощущения. Такое же архаическое, примитивное и гадательное впечатление производит и математика Николая Оресма, епископа Лизье (1323–1382), впервые на Западе введшего свободную разновидность координат и даже степени с дробными показателями, которые предполагают – еще неясное, но несомненно наличное – ощущение числа, которое всецело неантично, но в то же время не походит и на арабское. Рядом с Диофантом вспоминаются раннехристианские саркофаги из римских собраний, а рядом с Оресмом – готические задрапированные статуи из немецких соборов, и нечто родственное можно заметить также и в ходе математических рассуждений, которые представляют у того и другого одну и ту же раннюю ступень абстрактного понимания. Стереометрическое ощущение границы в последней отточенности и изяществе какого-нибудь Архимеда, что предполагает интеллигенцию мировой столицы, уже давно исчезло без следа. Повсюду в раннеарабском мире господствует смутный, тоскливый, мистический настрой, аттических ясности и свободы нет и в помине. Здесь живут земнородные люди раннего ландшафта, а не такие обитатели крупных городов, как Евклид и Д’Аламбер[53]. Глубокие и усложненные построения античного мышления здесь больше не понимали, но располагали спутанными и новыми, отчетливая духовно-городская формулировка которых будет получена еще не скоро. Вот готическое состояние всякой юной культуры, через которое сама античность прошла еще в раннедорическую эпоху, от которой не сохранилось ничего, за исключением керамики дипилонского стиля. Лишь в Багдаде в IX и X вв. зрелые мастера, не уступавшие Платону и Гауссу, провели до конца и завершили концепции ранней эпохи Диофанта.
8Решающим свершением Декарта, чья «Геометрия» вышла в свет в 1637 г., явилось не введение нового метода или точки зрения в области традиционной геометрии, как это постоянно изображают, но окончательная концепция новой идеи числа, которая выразилась в отделении геометрии от зрительных средств конструкции, вообще от измеренных и измеримых отрезков. Тем самым анализ бесконечно малых сделался свершившимся фактом. Декарт, если проникнуть в глубину его помыслов, не усовершенствовал жесткую, так называемую декартову систему координат, это идеальное представление измеримых величин в полуевклидовом смысле, которая имела величайшее значение в предыдущий период, например у Оресма, но ее преодолел. Его современник Ферма был ее последним классическим представителем.
На место чувственного момента конкретных отрезков и поверхностей, этого специфического выражения античного ощущения границы, заступает абстрактно-пространственный, а значит, неантичный момент точки, характеризуемой отныне как группа взаимноупорядоченных чистых чисел. Декарт уничтожил пришедшее из античных текстов и арабской традиции понятие величины, чувственного размера, и заменил его переменным значением соотношения положений в пространстве. Это было упразднение геометрии как таковой, которая начиная с этого момента ведет в пределах числового мира лишь призрачное, завуалированное античными реминисценциями существование, однако этого никто не заметил. Слово «геометрия» ни за что не отлучить от присутствующего в нем аполлонического смысла. Начиная с Декарта эта якобы «новая геометрия» представляет собой либо синтетическую деятельность, которая числами определяет положение точек в теперь уже не обязательно трехмерном пространстве («точечное многообразие»), либо аналитическую, которая определяет уже числа положением точек. Однако заменить отрезки положениями – это значит понимать протяжение теперь уже чисто пространственно, а не телесно.
Мне представляется, что классическим примером этого уничтожения наследия доставшейся от предыдущих поколений конечно-оптической геометрии является обращение круговых функций (которые в каком-то едва ли постижимом для нас смысле были «числами» индийской математики) в циклометрические с их последующим разложением в ряды, утратившие в бесконечной числовой области алгебраического анализа хотя бы самое отдаленное напоминание о геометрическом образе в духе Евклида. Число круга, π, возникая повсюду вновь и вновь в этой числовой области в качестве основания натуральных логарифмов е, порождает отношения, изглаживающие все границы прежних геометрии, тригонометрии и алгебры, которые не имеют теперь ни арифметического, ни геометрического характера: теперь в связи с ними никто более не имеет в виду ни действительно вычерченного круга, ни степеней, которые следует вычислить.
9Между тем как благодаря Пифагору ок. 540 г. античная душа пришла к открытию своего, аполлонического числа как измеримой величины, душа Запада в точно соответствующий временной момент отыскала благодаря Декарту и его поколению (Паскаль, Ферма, Дезарг) идею числа, родившуюся из неодолимого фаустовского пристрастия к бесконечному. Число как чистая величина, пристегнутая к телесному присутствию единичной вещи, находит свое контрастное подобие в числе как чистом отношении[54]. Если античный мир, космос, исходя из его глубокой потребности в зримой ограниченности, может быть определен как исчисленная сумма материальных вещей, то наше мироощущение осуществилось в картине бесконечного пространства, в котором все зримое, как обусловленное в противоположность необусловленному, воспринимается едва ли не как действительность второго порядка. Его символом оказывается решающее понятие функции, и намека на которое нет ни в одной другой культуре. Функция – это отнюдь не расширение какого бы то ни было из существующих понятий числа; она представляет собой полное его преодоление. Тем самым для действительно значимой математики Западной Европы утрачивает ценность не только евклидова, а значит, «общечеловеческая», основанная на повседневном опыте геометрия детей и профанов, но и архимедова сфера элементарного счета, арифметика. Отныне существует лишь абстрактный анализ. Для людей античности геометрия и арифметика были замкнутыми в самих себе и совершенными науками высшего ранга; процедуры той и другой были наглядными, имевшими дело с величинами через черчение или счет. Для нас же они – лишь практические вспомогательные средства повседневной жизни. Два античных метода вычисления величин, сложение и умножение, эти братья графических построений, полностью исчезают в бесконечности функциональных процессов. Сама степень, являющаяся поначалу лишь числовым обозначением определенной группы умножений (для произведений одинаковых величин), оказывается – в новом символе экспоненты (логарифма) и его применении в комплексной, отрицательной, дробной форме – всецело отделенной от понятия величины и переведенной в мир трансцендентных отношений, который должен был оставаться недоступным грекам, знавшим лишь две положительные, целочисленные степени в качестве представителей поверхностей и тел, – довольно будет привести такие выражения, как
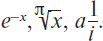
Все глубокие по мысли порождения, которые начиная с Возрождения стремительно следовали одно за другим, – мнимые и комплексные числа, введенные Кардано уже в 1550 г., бесконечные ряды, надежно обоснованные в плане теории великим открытием теоремы Ньютона о биноме, введенные ок. 1610 г. логарифмы, дифференциальная геометрия, открытый Лейбницем определенный интеграл, множество как новая числовая единица, намек на что имелся уже у Декарта, такие новые процессы, как неопределенное интегрирование, разложение функций в ряды, даже в бесконечные ряды других функций, – все это есть не что иное, как победы, одержанные над коренящимся в нас вульгарно-чувственным ощущением числа, которое следовало преодолеть исходя из духа новой математики с ее задачей воплощения нового мироощущения. Не было доныне второй такой культуры, которая окружала бы таким благоговением достижения другой, находилась бы под таким сильным ее влиянием в научном смысле, как это происходит с западной культурой по отношению к культуре античной. Много, очень много времени прошло, пока мы собрались с духом и стали пользоваться собственным мышлением. В основании этого лежало неизменное желание ни в чем не уступить античности. Тем не менее каждый шаг, делавшийся с этой целью, был на самом деле удалением от идеала, к которому стремились. Поэтому история западноевропейской науки представляет собой последовательное освобождение от античного мышления, – освобождение, которого никто вовсе и не желал, которое было навязано нам в глубинах бессознательного. Таким образом, развитие новой математики вылилось в негласную, долгую, увенчавшуюся в конце концов победой борьбу против понятия величины[55].
10Ориентированные на античность предубеждения мешали нам по-новому обозначить собственно западное число как таковое. Язык символов современной математики замазывает этот факт, и прежде всего на его счет следует отнести то, что еще и сегодня также и среди математиков господствует убеждение в том, что числа – величины, ибо на этой предпосылке, разумеется, и основывается наш способ письменных обозначений.
Однако новым числом являются не служащие для выражения функции отдельные символы (х, π, 5), а сама функция как единство, как элемент, как переменное отношение, более не вмещающееся в оптические границы. Для него понадобился бы новый, не находившийся под влиянием античных воззрений формульный язык.
Необходимо давать себе ясный отчет, чем отличаются друг от друга два таких уравнения (уже само одно это слово не должно было бы одновременно обозначать столь разноплановые вещи), как 3x + 4x = 5x и хn + уn = zn (уравнение теоремы Ферма). Первое образовано несколькими «античными числами» (величинами), второе представляет собой число другого рода, что оказывается сокрытым тождественным способом записи, который развился под впечатлением евклидовско-архимедовских представлений. В первом случае знак равенства является констатацией жесткой связи определенных, доступных чувствам величин; во втором – он устанавливает существующую внутри группы переменных образований связь такого рода, что определенные изменения необходимо влекут за собой другие. Цель первого уравнения – определение (измерение) конкретной величины, «результата»; у второго вообще нет никакого результата, а является оно лишь отображением и знаком отношения, которое исключает целочисленные значения для п > 2 (это и есть знаменитая проблема Ферма), что, возможно, удастся доказать. Греческий математик вообще бы не взял в толк, какова собственно цель операций такого рода, вообще не направленных на «вычисление» как таковое.
Понятие неизвестного всецело сбивает с толку, если применить его к буквам уравнения Ферма. В первом, «античном», x является определенной и измеримой величиной, которую следует получить. Во втором слово «определить» для х, у, z и п вовсе не имеет никакого смысла, и, следовательно, мы не желаем получать «значения» этих символов, т. е. они вообще не являются числами в скульптурном смысле, а знаками такой взаимозависимости, у которой вообще отсутствуют такие черты, как величина, образ и однозначность, знаками бесконечности возможных положений одного и того же характера, которые становятся собственно числами, лишь будучи осознаны как единство. Все уравнение в целом, в символьной записи, которая, к сожалению, использует много вводящих в заблуждение символов, фактически является одним-единственным числом, и х, у, z являются ими столь же мало, как + и =.
Ибо понятие конкретного, определенного числа оказалось в глубочайшем своем основании уничтоженным уже с введением понятия иррационального, всецело антигреческого числа. Теперь эти числа образуют уже не обозримый ряд нарастающих, дискретных, скульптурных величин, но поначалу одномерный континуум, каждое сечение которого (в смысле Дедекинда) представляет «число», которому вряд ли стоило давать это старое обозначение. Для античного ума между 1 и 3 существует лишь одно число, для западного – их здесь бесконечное множество. Наконец, с введением мнимых
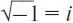
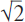
Классическим столетием этой барочной математики – в противоположность математике ионического стиля – явился XVIII в., который от решающих открытий Ньютона и Лейбница приводит через Эйлера, Лагранжа, Лапласа, Д’Аламбера к Гауссу. Бурный взлет этого мощного духовного творения происходил как чудо. Все едва отваживались на то, чтобы верить тому, что открывалось их глазам. Одна за другой отыскивались истины, представлявшиеся невозможными утонченным умам этой скептически настроенной эпохи. Это и имел в виду Д’Аламбер, сказав: «Allez en avant et la foi vous viendra» [Ступайте вперед, и обретете веру (фр.)]. Это относилось к теории дифференциала. Казалось, сама логика протестовала против того, чтобы основывать все предпосылки на погрешностях, и все же цель была достигнута.
Это столетие возвышенного упоения всецело абстрактными, отрезанными от телесного зрения формами (ибо рядом с этими мастерами анализа стоят Бах, Глюк, Гайдн, Моцарт), когда узкий кружок избранных и углубленных умов всецело предавался изысканным открытиям и отважным догадкам, отрезанными от которых оказались Гёте и Кант, в точности соответствует по содержанию наиболее зрелому столетию ионического стиля, к которому принадлежали Евдокс и Архит (440–350; к ним опять-таки следует присоединить Фидия, Поликлета, Алкамена и постройки Акрополя), когда весь мир форм античной математики и скульптуры расцвел во всей полноте своих возможностей и пришел к завершению.
Только теперь и возможно вполне обозреть элементарную противоположность античной и западной душевности. В пределах целостной картины истории высшего человечества невозможно – при таком множестве и силе исторических связей – отыскать ничего более чуждого друг другу. И как раз потому, что противоположности сходятся, что они, быть может, указывают на нечто общее в последнем основании бытия, мы находим в западной, фаустовской душе эту страстную тоску по идеалу аполлоническому, который она любила более всех прочих и которому завидовала из-за силы ее преданности чисто чувственному настоящему.
11Еще до нас замечено, что в прачеловечестве, как и в ребенке, происходит внутреннее переживание, рождение «я», благодаря которому они оба постигают смысл числа, а тем самым обретают соотносящийся с «я» окружающий мир.
Как только перед изумленным взглядом раннего человека из хаоса впечатлений крупными штрихами выделяется этот предрассветный мир упорядоченных протяженностей, осмысленно ставшего, и глубоко воспринимаемая неотвратимая противоположность этого внешнего мира и мира внутреннего придает направление и облик бодрствующей жизни, в этой внезапно осознавшей собственное одиночество душе тут же рождается прачувство томления. Это томление по цели становления, по завершению и осуществлению всех внутренних возможностей, по раскрытию идеи собственного существования. Это томление ребенка, которое с нарастающей ясностью входит в сознание в качестве чувства неудержимого направления и впоследствии возникает перед созревшим духом в форме загадки времени – тревожной, влекущей, неразрешимой. Слова «прошлое» и «будущее» внезапно обретают роковой смысл.
Однако это томление от переизбытка и блаженства внутреннего становления оказывается в то же самое время в самой потаенной глубине всякой души также и страхом. Как всякое становление направлено к ставшему, которым и завершается, так и прачувство становления, томление, уже соприкасается с иным ставшего – страхом. В настоящем мы ощущаем утекание, в прошлом заложена преходящесть. В этом корень вечного страха перед неизбежным, достигнутым, окончательным, перед преходящестью, перед самим миром как воплощенным, в котором одновременно с гранью рождения оказывается заданной и грань смерти, страх перед мгновением, в которое осуществляется возможное, внутренне исполняется жизнь, где сознание приходит к цели. Это тот глубокий мировой страх детской души, который никогда не покидает высшего человека, верующего, поэта, художника в их безграничном обособлении, страх перед чуждыми силами, которые во всем своем угрожающем величии, в обличье чувственных явлений, проникают в предрассветный мир. Также и направлению во всяком становлении во всей его неумолимости – необратимости – человеческое желание понять дает, как чему-то чуждому и враждебному, имена, с тем чтобы околдовать непонятное. Это есть нечто неуловимое, превращающее будущее в прошлое, и это придает времени в противоположность пространству ту полную противоречий жутковатость и гнетущую неоднозначность, от которой не способен до конца защититься никакой значительный человек.
Мировой страх – несомненно, самое творческое из всех прачувств. Это ему человек обязан самыми зрелыми и глубокими из всех форм и образов не только собственной сознательной внутренней жизни, но также и его отражениями в бесчисленных порождениях внешней культуры. Как некая тайная, доступная не всякому уху мелодия, страх проходит через язык форм всякого подлинного произведения искусства, всякой внутренней философии, всякого значительного поступка, и это он – доступный здесь еще меньшему числу людей – лежит в основе также и великих проблем всякой математики. Лишь внутренне умерший человек поздних городов – Вавилона Хаммурапи, птолемеевой Александрии, исламского Багдада или нынешних Парижа и Берлина, лишь этот чисто интеллектуальный софист, сенсуалист и дарвинист уходит от него или его отрицает, воздвигая между собой и чуждым лишенное тайны «научное мировоззрение».
Если томление связывается с тем неуловимым нечто, чьи тысячеликие неуловимые знаки присутствия скорее скрываются, чем обозначаются словом «время», то прачувство страха находит выражение в духовных, доступных, способных к преобразованию символах протяжения. Так, в бодрствовании всякой культуры, во всякой по-своему, присутствуют противоформы времени и пространства, направления и протяжения, причем первое лежит в основе второго, как становление – в основе ставшего (ибо также и томление лежит в основе страха, это оно делается страхом, а не наоборот); первое ускользает от силы духа, а второе стоит у нее на службе, первое служит только переживанию, второе только познанию. «Бояться и любить Бога» – вот христианское выражение противоположного смысла того и другого мироощущения.

