Искусственный интеллект в прикладных науках. Медицина

Глава 3. Прогнозирование эпидемий и распространения заболеваний

Роль искусственного интеллекта (ИИ) в прогнозировании эпидемических ситуаций становится все более значимой и важной в современном мире. ИИ обладает потенциалом для анализа больших объемов данных, выявления скрытых закономерностей и предсказания развития эпидемий на ранних стадиях. Он может помочь в выявлении и отслеживании распространения инфекционных заболеваний, оценке рисков и прогнозировании возможных сценариев развития ситуации.

Использование искусственного интеллекта (ИИ) в прогнозировании эпидемий открывает новые возможности для более точного и эффективного контроля за распространением инфекционных заболеваний. Одним из ключевых преимуществ такого подхода является способность ИИ обрабатывать огромные объемы данных с множеством переменных и факторов. В контексте эпидемиологии это означает учет широкого спектра параметров, включая географическое расположение, демографические характеристики населения, миграционные потоки, климатические условия, уровень доступа к медицинской помощи и многое другое.

ИИ позволяет анализировать эти данные с высокой степенью точности и выявлять скрытые закономерности, которые могут быть невидимы для человеческого восприятия. Например, системы машинного обучения могут выявлять связи между различными факторами и тенденциями распространения инфекции, что помогает более точно моделировать и прогнозировать эпидемические сценарии.

Благодаря использованию ИИ можно разрабатывать интеллектуальные системы, способные оперативно реагировать на изменяющиеся условия и адаптировать стратегии борьбы с эпидемией. Это позволяет быстрее и эффективнее принимать меры по контролю за распространением инфекций, направленные на минимизацию рисков для общественного здоровья. Таким образом, использование ИИ в прогнозировании эпидемий способствует улучшению реакции на угрозы здоровью и содействует более эффективному управлению пандемическими ситуациями.

ИИ также может быть использован для анализа данных о заболевших, таких как симптомы, медицинские истории, контакты с другими людьми и перемещения, что позволяет выявлять и прогнозировать потенциальные очаги заболевания, а также разрабатывать стратегии контроля и предотвращения распространения инфекций. Кроме того, с помощью методов машинного обучения и анализа данных можно проводить прогнозирование эффективности различных мер по борьбе с эпидемиями, таких как вакцинация, карантинные меры или массовое тестирование. В целом, использование ИИ в прогнозировании эпидемических ситуаций может значительно улучшить способность общества реагировать на угрозы здоровью и предотвращать пандемии.

Рассмотрим 10 моделей, которые часто используются для прогнозирования распространения инфекционных заболеваний:

1. SEIR-модель (Susceptible-Exposed-Infectious-Recovered): Эта модель является одной из самых распространенных и используется для моделирования распространения инфекционных заболеваний. В SEIR-модели каждый индивидуум в населении находится в одном из четырех состояний: подверженный (Susceptible), инфицированный, но не инфекционный (Exposed), инфекционный (Infectious) и выздоровевший (Recovered). Модель учитывает потоки людей между этими состояниями: здоровые могут заразиться и перейти в состояние инфицированных, инфицированные могут стать инфекционными и передавать болезнь другим, затем они могут выздороветь и стать иммунными к болезни. SEIR-модель позволяет моделировать динамику эпидемии, такую как скорость распространения инфекции и общее количество заболевших, что помогает оценить эффективность мер по контролю за заболеванием и прогнозировать его дальнейшее развитие.

Скелет модели SEIR представляет собой систему дифференциальных уравнений, описывающих динамику распространения инфекции в популяции. Вот как выглядит скелет SEIR-модели:

Рассмотрим пример реализации модели SEIR на языке Python с использованием библиотеки SciPy для решения дифференциальных уравнений:

```python

import numpy as np

from scipy.integrate import odeint

import matplotlib.pyplot as plt

# Функция, описывающая систему дифференциальных уравнений SEIR

def deriv(y, t, N, beta, sigma, gamma):

S, E, I, R = y

dSdt = -beta * S * I / N

dEdt = beta * S * I / N – sigma * E

dIdt = sigma * E – gamma * I

dRdt = gamma * I

return dSdt, dEdt, dIdt, dRdt

# Параметры модели и начальные условия

N = 1000 # Общее количество людей в популяции

beta = 0.2 # Коэффициент передачи болезни

sigma = 0.1 # Скорость перехода от инфицированного, но не инфекционного, к инфекционному состоянию

gamma = 0.05 # Скорость выздоровления или перехода от инфекционного к выздоровевшему состоянию

E0, I0, R0 = 1, 0, 0 # Начальное количество инфицированных, выздоровевших

S0 = N – E0 – I0 – R0 # Начальное количество подверженных

# Временные точки

t = np.linspace(0, 160, 160)

# Решение системы дифференциальных уравнений SEIR

y0 = S0, E0, I0, R0

ret = odeint(deriv, y0, t, args=(N, beta, sigma, gamma))

S, E, I, R = ret.T

# Построение графика

plt.figure(figsize=(10, 6))

plt.plot(t, S, 'b', alpha=0.7, linewidth=2, label='Подверженные')

plt.plot(t, E, 'y', alpha=0.7, linewidth=2, label='Инфицированные, но не инфекционные')

plt.plot(t, I, 'r', alpha=0.7, linewidth=2, label='Инфекционные')

plt.plot(t, R, 'g', alpha=0.7, linewidth=2, label='Выздоровевшие')

plt.xlabel('Время (дни)')

plt.ylabel('Численность')

plt.title('Модель SEIR для эпидемии')

plt.legend()

plt.grid(True)

plt.show()

```

Этот код решает систему дифференциальных уравнений SEIR и строит графики изменения численности подверженных, инфицированных, выздоровевших в течение времени. Пожалуйста, обратите внимание, что значения параметров и начальных условий могут быть изменены в зависимости от конкретной ситуации и характеристик заболевания.

Для написания кода модели SEIR в Python мы используем библиотеку SciPy для решения системы дифференциальных уравнений. Вначале мы определяем функцию, которая представляет собой систему уравнений для SEIR модели. Затем мы используем функцию `odeint` из библиотеки SciPy для решения этой системы уравнений на протяжении определенного временного интервала. В результате мы получаем временной ряд, показывающий изменение численности каждой группы (подверженные, инфицированные, выздоровевшие) с течением времени.

После получения результатов, мы можем визуализировать динамику эпидемии с помощью библиотеки Matplotlib, чтобы лучше понять, как распространяется инфекция в популяции. Например, мы можем построить графики для численности каждой группы на протяжении времени, чтобы увидеть, как количество зараженных, выздоровевших и подверженных меняется во времени.

Это позволяет нам оценить влияние различных параметров на динамику эпидемии и прогнозировать ее дальнейшее развитие. Такой подход позволяет исследователям и общественным организациям более точно понимать характеристики инфекционных заболеваний и разрабатывать эффективные стратегии борьбы с ними.

2. SIR-модель (Susceptible-Infectious-Recovered) является упрощенной версией SEIR-модели, где не учитывается состояние подверженных (Susceptible). В этой модели предполагается, что все люди, которые не выздоровели от болезни, уже инфицированы, и нет новых случаев заражения. Таким образом, SIR-модель описывает только два основных состояния популяции: инфицированные (Infectious) и выздоровевшие (Recovered).

Система дифференциальных уравнений для SIR-модели включает три уравнения, описывающих изменение численности каждой группы с течением времени. Первое уравнение описывает скорость изменения числа подвергшихся инфекции, которая уменьшается по мере того, как они выздоравливают и становятся иммунными к болезни. Второе уравнение описывает скорость изменения числа инфицированных, которая зависит от количества подвергшихся инфекции и скорости распространения болезни. Третье уравнение описывает скорость изменения числа выздоровевших, которая зависит от количества инфицированных и скорости выздоровления от болезни.

SIR-модель является полезным инструментом для анализа и прогнозирования эпидемических ситуаций, особенно в случаях, когда нет необходимости учитывать подверженные состояния или когда количество новых случаев заражения невелико. Эта модель может помочь оценить влияние различных факторов на динамику эпидемии и предсказать ее дальнейшее развитие, что позволяет принимать более информированные решения в области общественного здравоохранения.

Рассмотрим пример кода на Python для реализации SIR-модели:

```python

import numpy as np

from scipy.integrate import odeint

import matplotlib.pyplot as plt

# Определение функции, представляющей систему дифференциальных уравнений SIR-модели

def sir_model(y, t, beta, gamma):

S, I, R = y

dSdt = -beta * S * I

dIdt = beta * S * I – gamma * I

dRdt = gamma * I

return [dSdt, dIdt, dRdt]

# Начальные условия: количество подвергшихся инфекции, инфицированных и выздоровевших

S0 = 0.99

I0 = 0.01

R0 = 0.0

# Временные параметры

t = np.linspace(0, 200, 1000) # Временной интервал: от 0 до 200 дней, 1000 точек

# Коэффициенты модели: скорость передачи болезни (beta) и скорость выздоровления (gamma)

beta = 0.3

gamma = 0.1

# Решение системы дифференциальных уравнений

solution = odeint(sir_model, [S0, I0, R0], t, args=(beta, gamma))

# Построение графика

plt.plot(t, solution[:, 0], label='Подверженные') # Подверженные

plt.plot(t, solution[:, 1], label='Инфицированные') # Инфицированные

plt.plot(t, solution[:, 2], label='Выздоровевшие') # Выздоровевшие

plt.xlabel('Время (дни)')

plt.ylabel('Доля населения')

plt.title('Модель SIR')

plt.legend()

plt.grid(True)

plt.show()

```

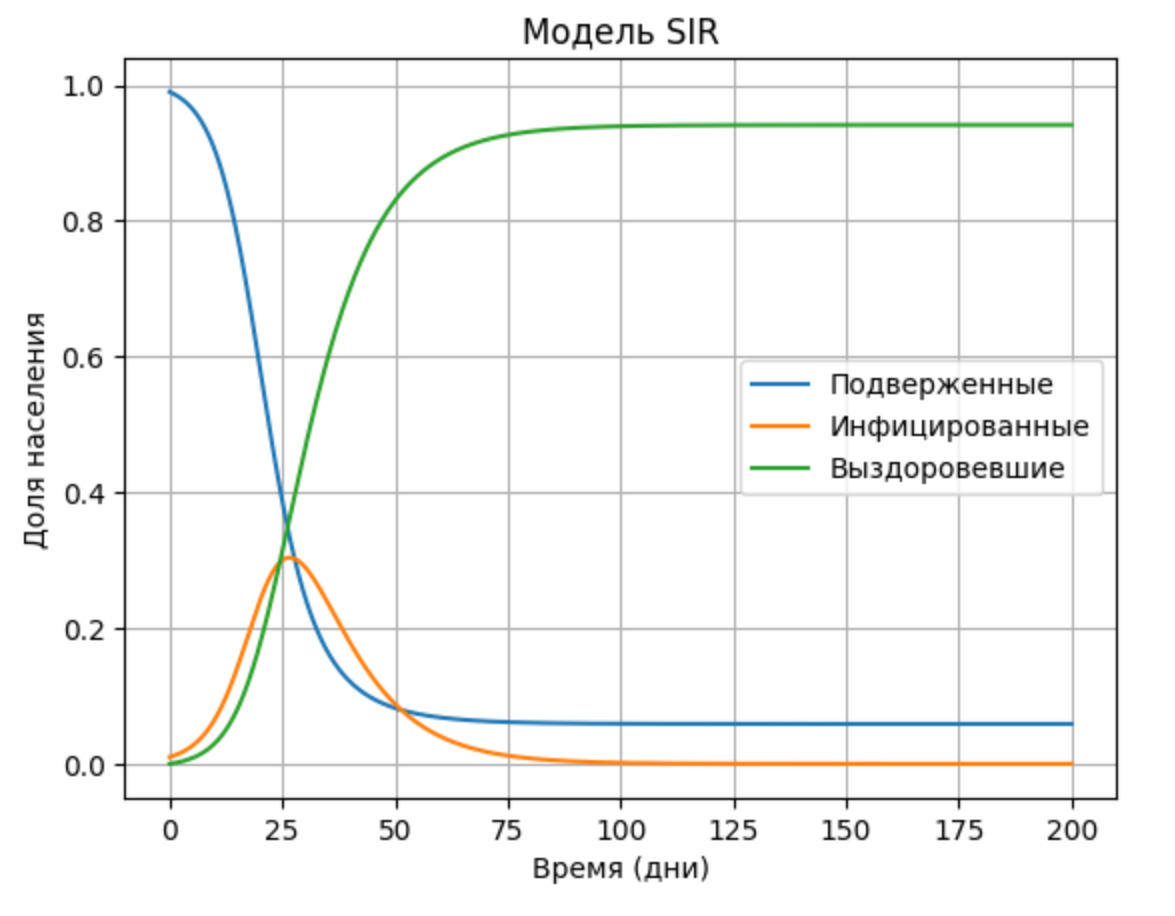
Этот код реализует SIR-модель для моделирования распространения инфекционного заболевания в популяции. Он использует библиотеки NumPy, SciPy и Matplotlib для выполнения численных вычислений, решения дифференциальных уравнений и визуализации результатов.

Комментарии в коде объясняют каждую часть программы: определение функции `sir_model` для системы дифференциальных уравнений SIR-модели, установка начальных условий и временных параметров, решение дифференциальных уравнений с помощью функции `odeint`, построение графика, показывающего изменение численности каждой группы (подверженные, инфицированные, выздоровевшие) с течением времени.

После выполнения кода, мы получаем графики, отображающие динамику эпидемии во времени. В результате мы увидим три кривые, представляющие количество подверженных инфекции (S), инфицированных (I) и выздоровевших (R) с течением времени.

– График для подверженных инфекции (S): На этом графике мы увидим, как количество подверженных инфекции уменьшается с течением времени, поскольку люди заражаются и становятся иммунными к болезни.

– График для инфицированных (I): Этот график показывает, как количество инфицированных меняется во времени. На начальном этапе количество инфицированных может расти, затем оно может достигнуть пика и начать снижаться по мере того, как люди выздоравливают от болезни.

– График для выздоровевших (R): На этом графике мы видим, как количество выздоровевших от болезни растет с течением времени, поскольку инфицированные люди выздоравливают и становятся иммунными к болезни.

Эти графики позволяют нам визуально оценить динамику эпидемии, а также определить основные параметры, такие как скорость распространения болезни и эффективность мер по ее контролю. Это позволяет принимать более обоснованные решения в области общественного здравоохранения для борьбы с эпидемией.

3. SEIRS-модель является вариантом SEIR-модели, которая в свою очередь является математической моделью для изучения распространения инфекционных заболеваний в популяции. В SEIR-модели популяция разделяется на четыре категории: подверженные инфекции (Susceptible), инфицированные (Exposed), инфицированные и инфекциозные (Infectious), и выздоровевшие или имеющие иммунитет (Recovered).

В SEIRS-модели добавляется дополнительная категория – Recovered with temporary immunity, что означает, что выздоровевшие имеют временный иммунитет перед тем, как вернуться в состояние подверженности инфекции. Это позволяет учесть факторы, такие как временное уменьшение иммунитета после выздоровления или длительный период времени, когда человек может быть вновь подвержен заражению после излечения.

Одна из ключевых особенностей SEIRS-модели – учет временного интервала между инфицированием и появлением симптомов заболевания. Этот интервал может варьироваться в зависимости от конкретного инфекционного заболевания и может быть важным фактором при прогнозировании распространения болезни и планировании мер по ее контролю. В целом, SEIRS-модель предоставляет более реалистичное описание динамики распространения инфекционных заболеваний в сравнении с более простыми моделями, не учитывающими временные аспекты и динамику иммунитета в популяции.

Давайте представим, что у нас есть небольшая популяция, состоящая из 1000 человек, и они подвержены вспышке инфекционного заболевания, например, гриппа. Мы будем использовать SEIRS-модель для иллюстрации динамики этой вспышки.

Начальные условия: Первоначально, все 1000 человек в популяции считаются подверженными инфекции (Susceptible).

Ввод параметров: Мы определяем параметры модели, такие как коэффициент передачи инфекции, коэффициент инкубационного периода, коэффициент выздоровления и длительность временного иммунитета.

Экспозиция (Exposed): Некоторые из подверженных инфекции начинают инкубационный период, в течение которого они инфицированы, но еще не заразны для других. Допустим, в первый день 50 человек становятся экспонированными (Exposed).

Инфекция (Infectious): По прошествии определенного времени после инкубационного периода, экспонированные становятся инфекциозными и могут заразить других. Предположим, что каждый инфицированный в среднем заражает 1,5 человека.

Выздоровление (Recovered with temporary immunity): После некоторого времени инфицированные выздоравливают и приобретают временный иммунитет к болезни. Например, допустим, что средняя продолжительность болезни составляет 7 дней.

Потеря временного иммунитета: После определенного времени временный иммунитет уменьшается, и ранее выздоровевшие снова становятся подверженными инфекции.

Повторение цикла: Процесс повторяется, пока большинство популяции не будет либо заражено, либо приобретет иммунитет.

Модель позволяет нам проследить динамику распространения болезни во времени, учитывая временные аспекты, такие как инкубационный период и временной иммунитет, что делает ее более реалистичной и полезной для прогнозирования и управления эпидемиологической ситуацией.

Рассмотрим пример простой реализации SEIRS-модели на языке Python с использованием библиотеки `numpy` для вычислений и `matplotlib` для визуализации:

```python

import numpy as np

import matplotlib.pyplot as plt

def seirs_model(beta, sigma, gamma, delta, susceptible, exposed, infectious, recovered, days):

N = susceptible + exposed + infectious + recovered

S = [susceptible]

E = [exposed]

I = [infectious]

R = [recovered]

for _ in range(days):

new_exposed = beta * S[-1] * I[-1] / N

new_infectious = sigma * E[-1]

new_recovered = gamma * I[-1]

new_susceptible = delta * R[-1]

susceptible -= new_exposed

exposed += new_exposed – new_infectious

infectious += new_infectious – new_recovered

recovered += new_recovered – new_susceptible

S.append(susceptible)

E.append(exposed)

I.append(infectious)

R.append(recovered)

return S, E, I, R

# Параметры модели

beta = 0.3 # Скорость инфекции

sigma = 0.2 # Скорость инкубационного периода

gamma = 0.1 # Скорость выздоровления

delta = 0.05 # Скорость временного иммунитета

susceptible = 990

exposed = 10

infectious = 0

recovered = 0

days = 160

# Запуск модели

S, E, I, R = seirs_model(beta, sigma, gamma, delta, susceptible, exposed, infectious, recovered, days)

# Визуализация результатов

plt.figure(figsize=(10, 6))

plt.plot(S, label='Susceptible')

plt.plot(E, label='Exposed')

plt.plot(I, label='Infectious')

plt.plot(R, label='Recovered')

plt.xlabel('Days')

plt.ylabel('Population')

plt.title('SEIRS Model')

plt.legend()

plt.grid(True)

plt.show()

```

Этот код создает функцию `seirs_model`, которая моделирует SEIRS-модель в течение определенного количества дней. Затем задаются параметры модели и вызывается функция `seirs_model` с этими параметрами. Результаты моделирования визуализируются с помощью библиотеки `matplotlib`.

На графике, полученном в результате выполнения этого кода, можно увидеть изменение численности каждой категории популяции (подверженные инфекции, инфицированные, выздоровевшие) в течение времени (в днях).

– "Susceptible" (подверженные инфекции) показывает, как меняется количество людей, которые могут быть инфицированы.

– "Exposed" (инфицированные, но еще не заразные) показывает количество людей, которые уже заразились, но еще не стали инфекциозными.

– "Infectious" (инфициозные) отображает количество людей, которые являются инфекциозными и могут передавать болезнь.

– "Recovered" (выздоровевшие) показывает количество людей, которые уже выздоровели от болезни и временно имеют иммунитет.

График позволяет визуализировать динамику эпидемии: как изменяется число подверженных инфекции, инфицированных, выздоровевших с течением времени в моделируемой популяции.

4. SIS-модель – это математическая модель, которая описывает динамику распространения инфекционных заболеваний в популяции, учитывая только переход между инфицированными и восприимчивыми состояниями, без учета выздоровления или приобретения иммунитета. В этой модели популяция делится на две основные категории: инфицированные (Infected) и восприимчивые (Susceptible).

Основное предположение SIS-модели состоит в том, что после инфицирования человек остается восприимчивым к заболеванию снова, после того как вылечится или станет носителем болезни. Это означает, что в модели нет категории выздоровевших или имеющих иммунитет.

Математически SIS-модель описывается системой дифференциальных уравнений, которые описывают скорость изменения численности инфицированных и восприимчивых во времени, учитывая параметры, такие как скорость заражения и скорость выздоровления. Эта модель может быть использована для прогнозирования динамики эпидемии, определения оптимальных стратегий контроля и оценки эффективности мер по борьбе с распространением инфекционных заболеваний.

Модель SIS, хоть и является простой, играет важную роль в изучении динамики распространения инфекционных заболеваний в популяции. Ее преимущество заключается в доступности и понятности как для исследователей, так и для практиков в области общественного здравоохранения. Универсальность этой модели позволяет применять ее для анализа различных эпидемических сценариев, не требуя сложных вычислений или данных.

Однако упрощенный характер модели означает, что она не учитывает некоторые ключевые аспекты реальной динамики заболевания. Основным ограничением является отсутствие учета приобретения иммунитета после инфекции или вакцинации. Это может привести к недостаточно точным прогнозам и рекомендациям при планировании мер по контролю за распространением болезни.

В то же время модель SIS остается ценным инструментом для идентификации рисков и прогнозирования тенденций в эпидемиологии. Она позволяет легко оценить влияние различных параметров, таких как скорость инфицирования и выздоровления, на динамику заболевания в популяции. Несмотря на свои ограничения, модель SIS остается важным инструментом для исследования основных механизмов распространения инфекционных заболеваний и разработки стратегий по их контролю.

SIS-модель представляет собой важный инструмент для изучения динамики распространения инфекционных заболеваний и принятия решений в области общественного здравоохранения, особенно там, где не предполагается приобретение стойкого иммунитета после выздоровления.

Рассмотрим пример реализации SIS-модели на языке Python с использованием библиотеки `numpy` для вычислений и `matplotlib` для визуализации:

```python

import numpy as np

import matplotlib.pyplot as plt

def sis_model(beta, gamma, susceptible, infected, days):

N = susceptible + infected

S = [susceptible]

I = [infected]

for _ in range(days):

new_infections = beta * S[-1] * I[-1] / N

new_recoveries = gamma * I[-1]

susceptible -= new_infections

infected += new_infections – new_recoveries

S.append(susceptible)

I.append(infected)

return S, I

# Параметры модели

beta = 0.3 # Скорость инфекции

gamma = 0.1 # Скорость выздоровления

susceptible = 990

infected = 10

days = 160

# Запуск модели

S, I = sis_model(beta, gamma, susceptible, infected, days)

# Визуализация результатов

plt.figure(figsize=(10, 6))

plt.plot(S, label='Susceptible')

plt.plot(I, label='Infected')

plt.xlabel('Days')

plt.ylabel('Population')

plt.title('SIS Model')

plt.legend()

plt.grid(True)

plt.show()

```

Этот код создает функцию `sis_model`, которая моделирует SIS-модель в течение определенного количества дней. Затем задаются параметры модели и вызывается функция `sis_model` с этими параметрами. Результаты моделирования визуализируются с помощью библиотеки `matplotlib`.

На графике, полученном в результате выполнения этого кода, можно увидеть изменение численности двух категорий популяции – восприимчивых к инфекции (Susceptible) и инфицированных (Infected) – в течение времени (в днях), согласно модели SIS.

– "Susceptible" показывает, как изменяется количество людей, которые могут быть инфицированы.

– "Infected" отображает количество людей, которые являются инфицированными и могут передавать болезнь.

График позволяет визуализировать динамику эпидемии, показывая, как число инфицированных и восприимчивых меняется в течение времени в моделируемой популяции.

5. Модель случайного блуждания – это абстрактная математическая модель, основанная на идее случайного перемещения индивидов и их контактах друг с другом. Эта модель предполагает, что каждый индивид перемещается в пространстве случайным образом, не зависящим от действий других людей, и встречается с другими индивидами случайным образом. Таким образом, модель отражает основные характеристики движения и контактов в реальных социальных сетях, что делает ее полезной для изучения распространения инфекций.

В рамках модели случайного блуждания каждый индивид представляется точкой или агентом в пространстве, который в каждый момент времени принимает случайное направление и перемещается на некоторое расстояние. Встречи между индивидами могут быть случайными и происходить с некоторой заданной интенсивностью.

Одним из ключевых применений модели случайного блуждания является оценка вероятности распространения инфекции в зависимости от перемещения людей. Путем моделирования случайных перемещений и контактов между индивидами можно определить, как вероятность заражения зависит от различных факторов, таких как плотность населения, скорость перемещения и частота контактов.

Однако важно учитывать, что модель случайного блуждания представляет собой упрощенную абстракцию реальной динамики социальных сетей, и ее применение может иметь ограничения в точности прогнозирования реальных ситуаций. Тем не менее, благодаря своей простоте и интуитивной понятности, модель случайного блуждания остается полезным инструментом для анализа и прогнозирования распространения инфекций в различных контекстах.