Как предсказать курс доллара. Эффективные методы прогнозирования с использованием Excel и EViews

Контрольные вопросы и задания к главе 1

1. Чем отличается строго стационарные процессы от стационарных процессов в широком смысле?

2. Может ли стационарный процесс иметь тренд или какие-либо строго периодические колебания?

3. Чем нестационарный процесс отличается от стационарного? Может ли у нестационарного процесса быть тренд?

4. Если Вы пришли к выводу о нестационарности данного временного ряда, то, что можно сказать об устойчивости его средней, дисперсии и автоковариации. Дайте определение средней, дисперсии и автоковариации.

Глава 2.

Метод наименьших квадратов и решение уравнения регрессии в Excel

2.1. Характеристика метода наименьших квадратов и его применение при прогнозировании курса доллара

Как мы выяснили в главе 1, динамика курса валют представляет собой временной ряд, имеющий не только тренд, но и случайную компоненту, поэтому в качестве метода оценки параметров прогностической модели, как правило, используется регрессионный анализ. Как известно, задачей регрессионного анализа является определение аналитического выражения (математической формулы), аппроксимирующего связь между зависимой переменной Y (ее называют также результативным признаком) и независимыми (их называют также факторными) переменными X1, X2…Xn. При этом форма связи результативного признака Y с факторами X1, X2…Xn, либо с одним фактором X, получила название уравнения регрессии. В качестве метода аппроксимации (приближения) в уравнении регрессии используется метод наименьших квадратов (МНК), который минимизирует сумму квадратов отклонений фактических значений Y от его предсказываемых значений, рассчитанных по определенной математической формуле. Причем, решение уравнения регрессии относительно интересующих нас переменных у (курс доллара) и х (время или порядковый номер месяца), по сути, заключается в подборе прямой линии к совокупности данных, состоящих из пар данных, характеризующих динамику курса доллара и соответствующие порядковые номера месяцев. При этом линию, которая лучше всего подойдет к этим данным, выбирают так, чтобы сумма квадратов значений вертикальных отклонений зависимой переменной (фактического курса доллара) от линии, рассчитанной по уравнению регрессии (предсказанный курс доллара), была минимальной.

Математические подробности оценки параметров уравнения регрессии методом наименьших квадратов

В самом общем виде формулу МНК можно представить следующим образом (2.1):

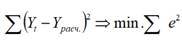
где Yt и Yрасч. – фактические и расчетные значения зависимой (результативной) переменной для различных моментов времени;

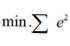
– минимальная сумма квадратов отклонений (остатков) фактических значений Y от его расчетных (предсказываемых) значений.

Поскольку Yрасч. =a +bX (где а – свободный член уравнения регрессии, а b – коэффициент регрессии), то уравнение (2.1) примет следующий вид (2.1.1):

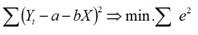
Для отыскания параметров a и b, при которых функция f(a,b) принимает минимальное значение, необходимо найти частные производные по каждому из параметров этой функции a и b и приравнять их нулю. Если минимальную сумму квадратов отклонений (остатков) e2 обозначить через S, то в результате мы получим систему нормальных уравнений МНК для прямой (2.1.2):

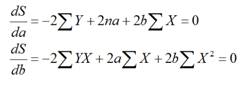
Преобразовав систему уравнений (2.1.2) получим (2.1.3):

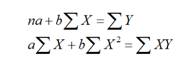
Решив систему уравнений (2.1.3) методом последовательного исключения переменных найдем следующие оценки параметров:

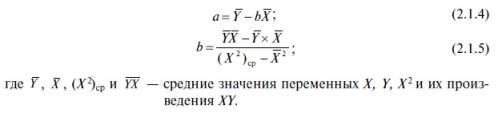
С помощью оцененного таким образом уравнения регрессии можно предсказать, как в среднем изменится признак Y в результате роста факторов X1, X2…Xt (или одного фактора X). В зависимости от того, какая математическая функция используется для прогнозирования результирующей переменной Y, различают линейную и нелинейную регрессию. При этом в основе линейной регрессии лежит уравнение линейного тренда, а в основе нелинейной регрессии – целое семейство уравнений нелинейных трендов (полиномиальный второй, третьей и прочих степеней, степенной, экспоненциальный, логарифмический и другие). В случае если результативный признак Y зависит от одного фактора X, то такое уравнение регрессии называется парным, а если Y зависит от нескольких факторов X1, X2…Xt – то уравнением множественной регрессии.

Практически в любом учебнике по общей теории статистики и по эконометрике можно более подробно познакомиться со спецификой уравнений регрессии. (См., например, учебник «Эконометрика» под ред. И.И. Елисеевой. – 2-е изд., пер. и доп. – М,: Финансы и статистика, 2006, стр. 43-132).

Существуют формулы, по которым можно самостоятельно найти параметры, как уравнения линейной регрессии, так и различных видов уравнений нелинейной регрессии. Однако с внедрением в широкую практику компьютеров и соответствующих компьютерных программ уже нет необходимости оценивать параметры уравнения регрессии вручную, тем более что этот процесс довольно трудоемкий.

2.2. Решение уравнения регрессии в Excel с учетом фактора времени. Интерпретация и оценка значимости полученных параметров

Поэтому далее остановимся на изучении алгоритма решения уравнений регрессии с применением соответствующих вычислительных программ. При этом работу с уравнениями регрессии в компьютерных программах можно разделить на три этапа.

На первом, подготовительном этапе необходимо определиться с набором факторов, которые необходимо включить в уравнение регрессии, а также с его аналитической формой, что в ряде случаев требует предварительной обработки данных. Например, в случае выбора степенного уравнения регрессии вместо исходных данных нужно взять их логарифмы.

Второй этап состоит из собственно решения уравнения регрессии и нахождения его параметров.

На третьем этапе проводится оценка и тестирования общего качества уравнения регрессии, проверка статистической значимости каждого из коэффициентов регрессии, определяются их доверительные интервалы, а также принимается окончательное решение об адекватности или неадекватности полученного уравнения регрессии.

Как известно, одним из наиболее распространенных способов определения тренда в динамике курса валюты является построение его зависимости от фактора времени T. Так, если в качестве зависимой переменной Y мы возьмем ежемесячный курс доллара, а в качестве независимой переменной T – время (в данном случае порядковые номера месяцев, начиная с июня 1992 г.=1), то у нас получится следующее уравнение парной линейной регрессии:

Y расч. =a + bT (2.2);

где a – свободный член уравнения регрессии; b – линейной коэффициент регрессии, показывающий, как изменение величины независимой переменной (фактора) T в среднем способствует изменению зависимой переменной (результативного признака) Y; Y расч. – расчетное значение результативного признака, вычисляемое по формуле (2.2).

Минимизируем сумму квадратов отклонений (остатков) Y факт. от Y расч.,то есть от фактических значений курса доллара от его расчетных значений. В результате формулу МНК (2.1.1) для линейной регрессии можно в данном случае представить в виде формулы (2.3):

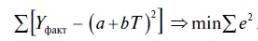
Уравнение (2.3) в принципе можно решить самостоятельно, если найти его параметры согласно формулам (2.1.4) и (2.1.5), но в целях ускорения этого процесса мы будем его решать с помощью Пакета анализа Excel. Кстати, желающие лучше усвоить суть МНК могут сначала самостоятельно в «ручном режиме» решить данное уравнение регрессии, а затем сверить свои результаты с теми, что мы получим в Excel.

Для того чтобы подготовить исходные данные к решению данного уравнения регрессии разместим в Excel два столбца исходных данных. В первом столбце, который озаглавим Time, поместим порядковые номера месяцев, начиная с июня 1992 г. (с номером =1) и кончая апрелем 2010 г. (с номером =215). Во втором столбце, который озаглавим USDOLLAR, поместим данные по курсу доллара на конец месяца, начиная с июня 1992 г. и заканчивая апрелем 2010 г. (последние данные, имевшиеся на тот момент, когда писались эти строки). Таким образом столбец Time представляет собой независимую переменную, которая в формуле (5) обозначена символом T, а столбец USDOLLAR является зависимой переменной Yфакт. Далее переходим к решению уравнения регрессии в Пакете анализа Excel, о том, как это делается, можно прочитать ниже – в алгоритме действий № 3.

Алгоритм действий № 3 «Как решить уравнение регрессии в Excel»

Шаг 1. Ввод в уравнение исходных данных

Делается это следующим образом: сначала в Microsoft Excel 2007 г. в верхней панели инструментов выбирается опция Данные (в Microsoft Excel 1997-2003 гг. нужно выбрать опцию Сервис), потом в появившемся окне Анализ данных – опция Регрессия. После чего появляется новое окно – Регрессия (см. рис. 2.1), в котором в графе Входной интервал y выделяем (с помощью мышки) столбец данных USDOLLAR (ячейки $C$1:$C$216). Здесь же в графе Входной интервал Х» выделяем столбец данных Time(ячейки $B$1:$B$216), то есть независимую переменную T из нашего уравнения регрессии (5).

Шаг 2. Дополнительные опции

Если бы мы хотели получить уравнение регрессии без свободного члена, который в формуле (2.2) обозначен символом a, то тогда нам следовало бы выбрать еще и опцию КОНСТАНТА-НОЛЬ. Однако в данном случае в использовании этой опции нет необходимости.

Опцию Остатки следует выбирать тогда, когда есть необходимость, чтобы в выходных данных содержалась информация об отклонении расчетных y от их фактических значений. При этом остатки находятся по следующей формуле (2.4):

Остатки = Yрасч.– Yфакт. (7); где Yрасч. – расчетные, Yфакт. – фактические значения результативного признака.

Опцию МЕТКИ применяют для того, чтобы переменные, включенные в уравнение регрессии, в выводе итогов были обозначены в виде заголовков соответствующих столбцов.

По умолчанию оценка в Excel параметров уравнения регрессии делается с 95% уровнем надежности. Однако в случае необходимости в опции Уровень надежности можно поставить цифру 99, что означает задание для программы оценить коэффициенты регрессии с 99% уровнем надежности. В результате в выводе итогов мы получим данные, характеризующие как в целом уравнение регрессии, так и верхние и нижние интервальные оценки коэффициентов данного уравнения с 95% и 99 % уровнями надежности. При 95% уровне надежности существует риск, что в 5 % случаях оценки коэффициентов уравнения регрессии могут оказаться неточными, а при 99% уровне надежности этот риск равен 1%.

Шаг 3. Вывод итогов

На заключительном этапе выбираем в параметрах вывода (окно РЕГРЕСССИЯ) опцию выходной интервал, в которой указываем соответствующую ячейку Excel ($H$2), далее щелкаем по надписи ОК и получаем ВЫВОД ИТОГОВ (см. рис 2.1, где можно увидеть все заданные нами параметры уравнения регрессии). В случае необходимости вывод итогов можно получить на отдельном листе (см. опцию НОВЫЙ РАБОЧИЙ ЛИСТ) или в новой книге Excel (см. опцию НОВАЯ РАБОЧАЯ КНИГА).

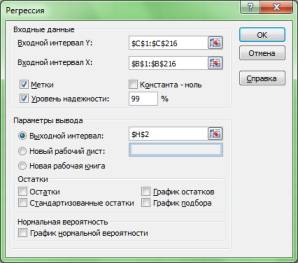
Рис. 2.1. Диалоговое окно РЕГРЕССИЯ для вывода итогов при решении в Excel уравнения регрессии

Результаты решения уравнения регрессии, которые в программе Excel выдаются в виде единой таблицы под заголовком ВЫВОД ИТОГОВ, у нас представлены в виде трех блоков (см. табл. 2.2-2.4). Так, в табл. 2.2 сгенерированы результаты по регрессионной статистике, в табл. 2.3 дается дисперсионный анализ, а в табл. 2.4 оценивается статистическая значимость коэффициентов регрессии .

Параметры, представленные в табл. 2.2, оценивают уровень аппроксимации фактических данных, полученный с помощью данного уравнения регрессии. Так, параметр Множественный R обозначает множественный коэффициент корреляции R, который характеризует тесноту связи между результативным признаком Y и факторами переменными X1, X2…Xn. Данный коэффициент изменяется в пределах от 0 до 1, причем, чем ближе к 1, тем теснее корреляционная связь между переменными, включенными в уравнение регрессии. Множественный коэффициент корреляции равен квадратному корню, извлеченному из коэффициента детерминации R2, который у нас также приводится в регрессионной статистике. Множественный коэффициент R также находят по формуле (2.5):

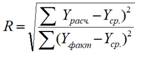
где Y факт. – фактическое, а Y расч. – расчетное (предсказанное по уравнению регрессии) значение результативного признака.

Зная величину коэффициента корреляции R, можно дать качественную оценку силы связи между зависимой и независимыми переменными, включенными в данное уравнение. С целью классификации силы связи обычно используют шкалу Чеддока (см. табл. 2.1).

Таблица 2.1. Шкала Чеддока для классификации силы связи

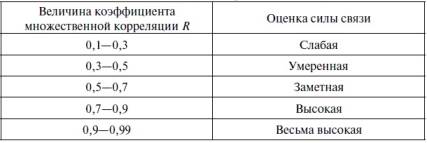
В случае между переменными существует функциональная связь, то R=1, а если корреляционная связь отсутствует, то R=0. Поскольку в таблице 2.2 множественный коэффициент корреляции R равен 0,8456, то согласно таблице Чеддока, связь между переменными, включенными в уравнение регрессии можно считать высокой. Следует также заметить, что если коэффициент множественной корреляции меньше 0,7, то это означает, что величина коэффициента детерминации R2 (о нем мы расскажем ниже) будет меньше 50%, а потому регрессионные модели с таким коэффициентом детерминации не имеют большого практического значения.

Однако самым важным является другой параметр регрессионной статистики – R-квадрат (его мы выделили жирным шрифтом), обозначающий коэффициент детерминации R2. Коэффициент детерминации R2 характеризует долю дисперсии результативного признака Y, объясняемую уравнением регрессии, в общей дисперсии результативного признака. Коэффициент детерминации R2 находится по формуле (2.6):

Конец ознакомительного фрагмента.

Текст предоставлен ООО «ЛитРес».

Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.