
Финансовая грамотность, или Основы управления личными финансами
Поэтому возникла альтернативная ординалистская теория полезности.
Кривая безразличия и бюджетная линия
Ординалистская (порядковая) теория полезности, основывается на том, что предпочтения потребителя относительно предлагаемых к выбору альтернатив не могут измеряться количественно, а только сравниваться. Потребитель выбирает – эта альтернатива хуже или лучше другой?
Согласно этой теории, невозможно измерить предельную полезность, так как потребитель измеряет не полезность отдельных благ, а полезность наборов благ. Предполагается, что измерению поддаётся порядок предпочтения наборов благ. Более глубокое объяснение поведение потребителя, когда он стремится максимизировать полезность, получаемую от приобретения двух товаров (разных благ) в условиях ограниченного бюджета, даётся при помощи кривой безразличия и бюджетной линии.
• Кривая безразличия – это множество всевозможных комбинаций благ, имеющих для потребителя одинаковую полезность, то есть потребителю безразлично какой набор товаров выбрать;
• Бюджетная линия (линия бюджетных ограничений) – показывает различные комбинации двух благ, которые потребитель может приобрести, при данном доходе и данных ценах.
Равновесие потребителя достигается, когда при определенных ценах и уровне дохода потребитель получает максимальную полезность от потребления набора товаров. В этой точке наклон бюджетной линии и кривой безразличия совпадает.
Чтобы подробнее ознакомиться с этими теориями, автор рекомендует читателю обратиться к специализированной литературе.
Санкт-петербургский парадокс
В 1738 году Даниил Бернулли предложил объяснение так называемого Санкт-Петербургского парадокса, иллюстрирующего расхождение между теоретически оптимальным поведением человека (игрока) и «здравым смыслом». Этот парадокс возник как математический казус и попытка найти всеобщий принцип (правило) принятия решений в условиях неопределённостей. Этот парадокс неявно сыграл важную роль в развитии экономических теорий и стал предтечей теории ожидаемой полезности.
Суть парадокса в следующем. Предлагается следующая игра: подбрасывается монетка до первого выпадения орла. По итогам игры выплачивается выигрыш в размере 2N-1 руб., где N – номер броска, на котором выпадет орёл.
Вопрос: сколько бы вы заплатили за участие в такой игре? Или, в другой формулировке, при каком вступительном взносе игра становится выгодной (то есть игрок выиграет больше, чем заплатит)?
При каждом подбрасывании вероятность выпадения орла 1/2 или 0,5 (так как монетка выпадет либо орлом, либо решкой). При этом предыдущий результат подбрасывания не оказывает влияние на результат последующего подбрасывания. Каждое подбрасывание независимо друг от друга. Если орёл выпадает при первом броске, то выигрыш составит 1 рубль. Если орёл выпадает при втором броске, то выигрыш составит 2 рубль. Если орёл выпадает при третьем броске, то выигрыш составит 4 рубля. При четвёртом – 8 рубля и т.д. Другими словами, выигрыш, возрастая от броска к броску вдвое, последовательно пробегает степени двойки – 1, 2, 4, 8, 16, 32 и так далее.
Другими словами, подходящим математическим описанием данной ситуации, является случайная величина х, принимающая значения × = 2N-1, с вероятностью р = 2-N. Требуется найти значение, которое в определённом смысле эквивалентно указанной величине. В качестве такого эквивалента случайных величин (в данном случае цена участия в игре) используют математическое ожидание (как справедливую цену азартной игры). Математическое ожидание есть среднее значение случайной величины, которая считается по следующей формуле:
М(х) = р1х1 + р2х2 + … рnхn,
где р1, р2, …рn – вероятность каждого исхода, х1, х2, …хn – значение каждого исхода.
Математическое ожидание выигрыша:
• N=1 (при первом подбрасывания составляет), р1х1 = 2-N * 2N-1= 0,5*20 = 0,5 руб.;
• N=2 (при втором подбрасывания составляет), р2х2= 2-N * 2N-1= 0,25*21 = 0,5 руб.;
• N=3(при третьем подбрасывания составляет), р3х3= 2-N * 2N-1= 0,125*22 = 0,5 руб.;
• И т.д.
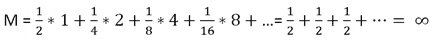
Как видим, для данной задачи математическое ожидание выигрыша бесконечно.
Это означает, что формально игрок может получить бесконечно большой выигрыш, однако большинство людей уклонится от участия в такой игре. Именно по этой причине и используется слово «парадокс» в названии задачи.
Иными словами, ожидаемый денежный выигрыш в игре бесконечен, однако рациональный игрок не готов заплатить за возможность участие в ней даже весьма небольшую цену. Казалось бы, какую бы цену организатор игры не запрашивал, в ней выгодно участвовать, так как ожидаемый выигрыш бесконечно велик, но на таких условиях найдётся мало желающих, готовых поучаствовать в игре.
Почему это так? Для объяснения этого, Бернулли предположил, что люди максимизируют не ожидаемый выигрыш, а ожидаемую полезность от выигрыша.
Теория ожидаемой полезности
Очевидно, что когда потенциального участника игры просят сделать бесконечно большой взнос, желающих не будет. Но, если условия азартной игры не будут явно нечестными, всегда можно будет найти желающих поучаствовать в ней. Всё дело в цене входа, приемлемого для участников и организаторов игры. Игроки готовы играть в эту игру, но за право участия в ней согласны платить сравнительно небольшие суммы (а кто не согласился бы на таких условиях?), при этом организаторы игры готовы играть и согласны принимать конечную ставку, при этом рискуя потенциально неограниченным проигрышем (уже не так очевидно почему они идут на это?).
Если считать что люди ведут себя как рациональные агенты, тогда должна работать так называемая «теория ожидаемой полезности» – формула, которая может использоваться рациональным игроком при принятии решений. Здесь предполагается, что каждый стремиться максимизировать благо (в терминах азартной игры – выигрыш).
Но многое говорит о том, что поведение людей скорее нерациональное, а иррациональное. И даже более того, наше иррациональное поведение не является случайным или бессмысленным, а является систематическим и предсказуемым (подробно описывается в теории перспектив, о которой поговорим далее).
Например, если предложить человеку сыграть в игру и дать два варианта на выбор:
1) Возможность получить 5 тыс. руб. с вероятностью 5 %;
2) Возможность получить 100 руб. с вероятностью 100 %.
Большинство людей, при таких условиях, выбирает второй вариант – с меньшим риском, но и с меньшим математическим ожиданием. В первом варианте математическое ожидание равно 250 руб. (5,000 × 5 %). Во втором варианте математическое ожидание равно 100 руб.
Для описания поведения, при котором люди предпочитают гарантированную выплату (не смотря на её меньшее математическое ожидание) была придумана формула ожидаемой полезности как инструмент анализа выбора в условиях риска. В 1944 году вышла монография Джона фон Неймана[23] и Оскара Моргенштерна «Теория игр и экономическое поведение», в которой авторы обобщили и развили результаты теории игр и предложили новый метод для оценки полезности благ. Они показали, что в условиях неполной информации рациональным выбором человека будет выбор варианта с максимальной ожидаемой полезностью. Не смотря на то, что концепция Неймана-Моргенштерна вдохнула новую жизнь в концепцию кардиналистской полезности, она далеко не всегда может объяснить поведение людей.
Рассмотрим другой пример. Вам предлагают сыграть в следующую игру. В закрытой коробке находится 99 белых шариков и 1 чёрный шарик. Вам нужно в слепую вытащить один шарик. Если вы вытяните белый – то вы потеряете всё то, что имеете. А если вытяните чёрный шарик – получите от организаторов 1 млрд. долларов. Допустим, у вас есть в собственности квартира, автомобиль и другие ценности общей стоимостью 100 тыс. долларов, что и будет, является величиной потенциального проигрыша.
По математике игра чрезвычайно выгодная для вас (математическое ожидание выигрыша будет 10 млн. долларов = 1 млрд. * 0,01). С вероятностью 0,01 можно выиграть 1 млрд. долларов. Но в данном конкретном случае, подавляющее большинство людей всё же откажется от участия в такой игре (хотя при этом будут продолжать покупать лотерейные билеты с гораздо меньшей вероятностью выиграть гораздо меньший потенциальный выигрыш).
На этом примере становится понятным, что даже лишь при двух исходах и с огромным средним выигрышем «рациональное» поведение людей не гарантированно. Без всякой математики условия данной игры для большинства людей кажутся неприемлемыми.
Поэтому приходится допустить, что рациональное поведение не есть простое стремление к максимизации блага (выигрыша).
Такое поведение людей, можно частично разрешить, если в качестве гипотезы принять, что когда мы говорим о бесконечном ряде стоимостных величин, потенциальный участник игры оценивает не столько сумму выигрыша, сколько ожидаемую полезность выигрыша. Полезность (ценность) ожидаемого рубля будет всегда ниже полезности предшествующего. Вот представьте, что вы заработали свой первый миллион рублей (или долларов, или евро – не суть). Полезность первого миллиона для вас самая максимальная. Затем появляется второй, третий, … десятый, двадцатый, … сотый и т.д. По мере насыщения полезность каждого последующего миллиона снижается (первый закон Госсена в действии). Кстати, отсюда напрашивается вывод о нелинейной полезности денег (хотя в большинстве случаев полезность можно отождествлять с деньгами).
Но парадокс разрешен лишь частично, так как потенциальные участники игры по-разному определяют собственную функцию полезности. Вывод простой и очевидный: в условиях неопределенности нельзя предсказать поведение потенциальных участников игры, поскольку неизвестны их функции полезности. Отсюда и возникает идея классификации участников в контексте их отношения к риску.
У каждого человека есть собственное отношение к риску, иначе говоря, к возможности потери денег. Принято выделять три категории:
• Нейтральные к риску;
• Любители риска;
• Противники риска.
Кто-то предпочитает не рисковать и не предпринимать рисковых действий, а кто-то, в этих же обстоятельствах готов рискнуть в надежде получить больше. Для объяснения выбора различных вариантов поведения, необходимо использовать концепцию ожидаемой полезности.
Практика показывает, что в большинстве люди всё-таки не склонны к риску. Такое поведение, помимо особенностей человеческой психики, обычно объясняется экономической причиной, а именно: действием закона убывающей предельной полезности.
У вас есть 100 руб. вам предлагают сыграть в «орёл/решка» и поставить 50 руб. В случае выпадения орла – вы получаете 50 руб. Выигрыша и в итоге у вас будет 150 руб. Если выпадет решка, то у вас в итоге будет 50 руб. То есть с вероятностью 1/2 выигрываете 50 руб. и с вероятностью 1/2 проигрываете 50 руб. Математическое ожидание равно 0, так как 0,5*50 + 0,5*(-50) = 0.
Если схематично изобразить на кривой совокупной полезности, то наглядно увидим, что ожидаемая полезность будет иметь отрицательное значение. В условных единицах полезности (числа выбраны произвольно) проигрыш будет равен -3 = 5–8, а выигрыш +1 = 9–8, что в сумме даёт "-2".
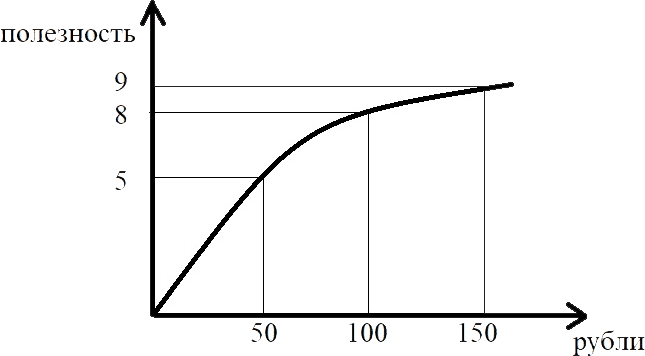
Рисунок 7. Кривая совокупной полезности игры «орёл-решка».
В случае проигрыша ваши убытки в условных единицах полезности по величине будут больше, чем выигрыш (3 против 1 условной единицы). Хотя в денежном выражении и проигрыш и выигрыш равны 50 руб. каждый. Именно потому, что рассуждая в терминах полезности ситуация выглядит иначе, чем рассуждая в терминах денег и необходимо различать математическое ожидание суммы выигрыша и её ожидаемую полезность.
Ваши негативные эмоции от потери 50 руб. будут сильнее примерно в 2 раза, чем ваши радостные эмоции от находки такой же суммы денег. Надо будет найти как минимум 100 руб., чтобы эмоционально компенсировать потерю 50 руб. Конечно, вам доставит радость получить больше того, что вы имеете, но для вас гораздо ощутимее будет потеря того, к чему вы уже привыкли.
Человек больше ценит те вещи, которыми уже владеет, а не те, которыми может овладеть. В экономической теории данный феномен получил название эффекта владения. В классической экономической теории этот эффект невозможно объяснить. Но объяснить этот и многие другие эффекты удалось Даниэлю Канеману, опираясь на теорию перспектив. Его совместная работа с Амосом Тверски привела к созданию «поведенческой экономики».
Теория перспектив или поведенческие финансы
Предлагаем вашему вниманию небольшую задачку. Попробуйте её решить самостоятельно и дать ответ, прежде чем продолжите чтение.
1. Ананас + яблоко стоят 110 руб.
2. Ананас стоит на 100 руб. дороже яблока.
ВОПРОС: Сколько стоит яблоко?
Теория была создана в 1979 году и развита в 1992 году Даниэлем Канеманом и Амосом Тверски. В 2002 году, несмотря на то, что Канеман проводил исследования как психолог, а не как экономист, ему была присуждена Нобелевская премия по экономике «за применение психологической методики в экономической науке, в особенности – при исследовании формирования суждений и принятия решений в условиях неопределённости».
Отталкиваясь от эмпирических наблюдений и свидетельств, теория описывает как люди оценивают потери и выигрыши. Эта теория описательная: она моделирует решения, принимаемые в реальной жизни, а не оптимальные решения, следующие из теории ожидаемой полезности. Одним из недостатков теории ожидаемой полезности является то, что в ней не учитывается такое явление как избегание рисков (неприятие потерь), что есть следствие того, что люди переоценивают маленькие вероятности и недооценивают большие.
Теория перспектив – это экономическая теория, которая сформулирована индуктивно (на основе экспериментов), и описывает поведение людей при принятия решений, связанных с рисками. Как люди принимают решения в ситуации неопределенности? Как выбирают между альтернативами, вероятности различных исходов в которых не известны. Каждый возможный исход имеет определенную вероятность возникновения и ценность, которую человек определяет субъективным образом. Причём ценности могут быть положительными, так и отрицательными (то есть потери человека).
В 1970-е годы общепринятыми считались два предположения. Во-первых, что люди в основном рациональны. Во-вторых, что большинство отклонений от рациональности объясняется эмоциями. Но исследования Канемана показали, что постоянные ошибки мышления людей обусловлены скорее самим механизмом мышления, нежели влиянием эмоций. Наши умы склонны к систематическим ошибкам или когнитивным искажениям, которые предсказуемо возникают в одних и тех же обстоятельствах.
Обычно вы можете сказать, о чём думаете. Процесс мышления кажется понятным: одна осознанная мысль закономерно вызывает следующую. Но разум работает не только так; более того, в основном он работает по-другому. Большинство впечатлений и мыслей возникает в сознании неизвестным вам путём. Как сказал автор теории: «… мы знаем о себе гораздо меньше, чем нам кажется».
В центре теории перспектив лежит три когнитивных свойства.[24] Они играют главную роль в оценке финансовых исходов и обычны для многих автоматических процессов восприятия, суждений и эмоций:
1. Оценка осуществляется относительно начальной точки отсчёта. Температура в квартире как точка отсчёта. Один вышел из ванны – ему кажется в квартире прохладно, другой зашёл с улицы с мороза – для него в квартире тепло.
2. Нелинейная оценка вероятностей. Разница между 900 руб. и 1000 руб. субъективно оценивается намного меньше разницы между 100 и 200 руб.
3. Неприятие потерь. Потери кажутся крупнее, чем выигрыш.
Эти три принципа, можно проиллюстрировать с помощью следующего графика, который показывает психологическую ценность выигрышей и потерь.
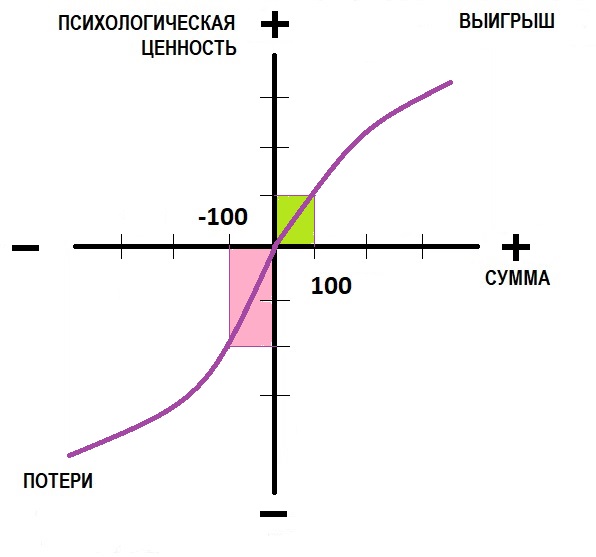
Рисунок 8. График психологической ценности потери/выигрыша.
Две половинки S-образной кривой не симметричны относительно вертикальной линии. Кривая изменяет свой характер в точке пересечения (точки отсчёта). Это происходит из-за того, что в большинстве случаев реакция человека на потери сильнее, чем его же реакция на соответствующий выигрыш. Это и есть проявление неприятия потерь. Горечь от потери 900 руб. больше, чем 90 % горечи от потери 1 тыс. руб. Иначе говоря, для большинства из нас страх потери 1 тыс. руб. сильнее надежды на выигрыш 1,5 тыс. руб.
Степень неприятия потери можно измерить самостоятельно, спросив себя: какой минимальный выигрыш уравновесит для меня равную вероятность потерять 100 руб.? Для большинства людей – будет примерно 200 руб., то есть вдвое больше проигрыша. При этом неприятие потерь у одних людей больше, у других меньше. Люди, профессионально рискующие на финансовых рынках, спокойней относятся к потерям – возможно потому, что не реагируют эмоционально на каждое колебание рынка.
Автор теории утверждает, что:
• В смешанных случаях, когда возможны и выигрыши, и потери, неприятие потерь приводит к выбору, при котором неприятие потерь максимально.
• В заведомо проигрышной ситуации, когда гарантированный проигрыш сравнивается с большей потерей, которая лишь вероятна, снижение чувствительности вызывает стремление к риску.
Эти два вывода – суть теории перспектив.
Давно известно, что на фондовом рынке инвесторы достаточно быстро продают те акции, которые выросли в цене, но достаточно долго держат те акции, которые упали в цене и продолжают падать. Основываясь на экспериментальных исследованиях, теория перспектив делает парадоксальный вывод: люди скорее готовы взять на себя больший риск, чтобы избежать потерь, чем получить дополнительную прибыль при большом риске. Этот феномен называется «неприятие потерь».
Посмотрите на два варианта ниже и выберите тот ответ, который вам больше нравится.

Более 80 % людей в первой ситуации выбирают ответ «А». И более 90 % людей во второй ситуации выбирают ответ «Б». Но если бы люди поступали рационально, тогда в первой ситуации следовало бы выбрать вариант «Б», а во втором – «А».
В подобных рисковых ситуациях, потребитель должен считать математическое ожидание и выбирать наилучший вариант.
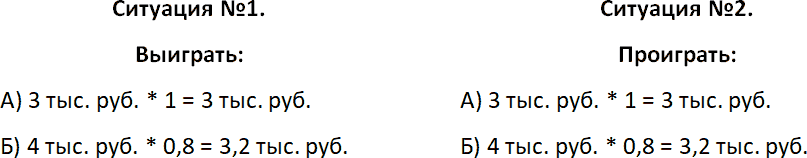
Но большинство людей выбирает то, что выбирает и это происходит из-за «неприятия потерь». Субъективно каждый проигранный рубль значит больше чем выигранный. Вот именно это, в первой ситуации толкает сделать выбор варианта «А», а во второй ситуации – «Б».
На заметку. Одно из возможных объяснений «магии бесплатного» – первое занятие бесплатно, беспроцентный кредит, бесплатное обслуживание, купи две вещи, а третья в подарок и т.д. – как раз и может заключаться в неприятии потерь. Почему для нас всё то, что бесплатно так притягательно? Даже если что-то тебе не надо, но оно бесплатно, тогда надо! Почему так?
Когда нам надо сделать выбор между чем-то и чем-то, то в большинстве подобных ситуаций будут как свои плюсы, так и минусы. Но когда предлагают нам что-то бесплатно, мы забываем про минусы и не видим возможности что-то потерять. Когда мы выбираем платный вариант, всегда присутствует риск неверного выбора или неправильного решения, которые может привести к потери. Поэтому, когда предлагают на выбор, мы склонны выбирать бесплатное, хотя, скорее всего, это лишь выглядит на первый взгляд как «бесплатное».
Допустим, девушка идет по торговому центру и видит: «Купи удлиняющую тушь для ресниц 3D с эффектом подкручивания и получи гель для душа в подарок». Тушь семьсот рублей стоит плюс гель за двести рублей – сложить не так сложно и в уме. Выгодно! Тут бесплатно гель предлагают, двести рублей сэкономить можно. А ведь в голову даже не приходит, что ещё совсем недавно гель, да и тушь сама, не нужны были, пока рекламу не увидели. Если так сильно гель нужен был, то можно было бы просто так купить за 200 руб. – не так ли? При этом реально удалось бы сэкономить 500 руб. Но «магия бесплатного» сработала и минус 700 руб.
Другой пример. Допустим, есть два человека и у каждого есть 1 млн. руб. Теория ожидаемой полезности гласит, что они оба должны быть одинаково счастливы. Но если мы учтём, что у первого вчера ничего не было и он сегодня выиграл в лотерею 1 млн. руб., а у второго ещё вчера было 3 млн. руб., а сегодня остался 1 млн. руб., то становиться очевидным тот факт, что они определённо не могут быть одинаково счастливы. У каждого была своя точка отсчёта. Теория ожидаемой полезности не рассматривает такие детали и просто ставит знак равенства между текущим количеством денег и счастьем человека. Теория перспектив учитывает, поэтому она и вышла на первый план благодаря своей лучшей точности моделирования реальных ситуаций.
Пример с яблоком и ананасом, приведенный в начале главы, показывает, как мы, люди, привыкли думать. Если вы ответили, что яблоко стоит 10 руб., то вы относитесь к подавляющему большинству людей, которые дают неправильный ответ. Автор задавал этот вопрос своим знакомым – и каждый раз все давали неправильный ответ… увы, когда автор впервые столкнулся с оригинальным вопросом в книге, то тоже дал быстрый и неверный ответ.
Десять рублей это не правильный ответ! Если яблоко стоит 10 руб., тогда ананас должен стоить 110 руб. (ведь по условиям задачи ананас стоит на 100 руб. дороже яблока). В сумме получается 120 руб. (10+110). Но это не может быть верным ответом, так как вместе они стоят 110 руб. Правильный ответ – яблоко стоит 5 руб., тогда ананас будет стоить 105 руб., что в сумме составит 110 руб. (105+5).
Когда вы быстро выдали ответ – 10 руб., это означает, что при решении этой задачи у вас сработала автоматическая Система № 1. Всего Канеман выделяет две системы:
• Система 1: срабатывает автоматически и очень быстро, почти не требуя усилий и не давая ощущения намеренного контроля.
• Система 2: выделяет внимание, необходимое для сознательных умственных усилий, в том числе для сложных вычислений.
В оригинале книга, описывающая эти системы, называется «Thinking, Fast and Slow», что можно перевести как «Мышление: быстрое и медленное». Оригинальное название отражает суть многолетних психологических исследований автора, который показывает нам на многочисленных примерах, что в нас есть две системы мышления: быстрая и медленная, то есть Система 1 и Система 2. Подробнее с самой теорией можно ознакомится в, уже вышеупомянутой, книге, которая в русском варианте была издана под названием «Думай медленно… решай быстро».
Проведенные Канеманом исследования не только не оторваны от реальной жизни, но и имеют достаточно конкретный, прикладной характер. Именно поэтому, с точки зрения автора, каждому, кто стремиться повысить свою финансовую грамотность, необходимо подробно ознакомиться с этой теорией и прочитать данную книгу.
Ведь даже само знание о том, что мы не в силах избежать когнитивных искажений, возможно, однажды поможет остановиться на несколько секунд, задуматься (то есть заставить работать Систему 2) и попытаться сделать оптимально возможный выбор, в ситуации, когда не до конца будет понятно верный выбор или нет.
В дополнение к вышеизложенному, хотелось бы ещё упомянуть и о том, что наш мозг воспринимает информацию только в окружении какого-либо контекста. Всегда.

Рисунок 9. Мозг воспринимает информацию только в окружении контента.
Только убрав окружающий контекст, мы можем понять, что центральные круги в действительности равны. Но, даже зная, что центральные круги одинакового диаметра, нам всё равно кажется, что они изменяют свой размер в зависимости от того, какого диаметра круги их окружают.
Этот простой рисунок отражает принцип нашего мышления. Мы всегда смотрим на вещи с учётом их окружения и сравниваем их с другими. От этого тяжело избавиться. Мы сравниваем не только материальные предметы – автомобили, одежду, еду, телефоны и т.д. – но и не материальные – один вариант отпуска с другим, один вариант ответа с другим, одну работу с другой и т.д.
Хотите увидеть, как это работает в реальности? Зайдите в любой супермаркет бытовой техники и скорее всего там увидите что, товары на полке располагают определённым образом – дорогой товар, средний, дешевый. Например, чайник 3500 руб., затем 1490 руб., и 550 руб. Вы думает три с половиной тысячи дороговато, на этом фоне чайник за 550 руб. выглядит вообще как-то откровенно дёшево, а вот за 1490 руб. самое то. И покупаете то, что надо продать магазину. А если добавить в этот ряд еще более дорогой товар (чайник за 5 тыс. руб.), то средняя цена покупки вырастет ещё больше, так как контекстная цена вокруг выросла (это работает «эффект привязки» – когнитивное искажение, подробнее о котором поговорим далее).