
Основы статистической обработки педагогической информации
По аналогии можно задавать свойства объекта geom вручную, например, можно сделать все точки на диаграмме зелеными, если использовать следующий синтаксис:
geom_point(mapping = aes(x = displ, y = hwy), color = "green")
Здесь цвет не передает информацию о переменном, он только меняет внешний вид графика. Устанавливая параметры вручную, можно регулировать общий стиль диаграмм. В частности, форму точек можно задавать порядковыми номерами, например, 0, 15 и 22 – это квадраты, разница между ними заключается в том, что некоторые залиты сплошным цветом. Полые формы (0-14) имеют границу, определяемую значением параметра color; сплошные формы (15-18) заполнены цветом указанным в color; а заполненные формы (21-24) имеют границу, совпадающую с цветом заливки.
Упражнения
1. Как сделать цвет всех точек графика синим?
2. Какие переменные в базе mpg являются категориальными? Который переменные являются непрерывными? (Подсказка: найдите в документации описание типов полей таблицы mpg). Где найти эту информацию при открытии справки по mpg?
3. Сопоставьте непрерывную переменную с цветом, размером и формой. Как такие настройки эстетики поведут себя для категориальных в отличии от непрерывных переменных?
4. Что произойдет, если сопоставить одну и ту же переменную с несколькими эстетиками?
5. Что делает эстетика stroke? В каких случаях она применима? (Подсказка: в документации найдите описание функции geom_point, для этого в консоли можно ввести ?geom_point)
6. Что произойдет, если сопоставите эстетику с чем-то другим, не являющимся именем переменной, например color = displ < 5? Как и прежде предварительно нужно будет указать значения параметров x и y.
Когда начнете выполнять код R, возможны некоторые затруднения. Не волнуйтесь, это случается со всеми. Автор книги тоже писал код R, в течение многих лет, который работает не сразу. Начните с тщательного сравнения кода, который используете, с кодом из книги. R чрезвычайно придирчив. Убедитесь, что каждая открывающаяся скобка «(«соответствует закрывающейся «)», а каждая кавычка «"» имеет парную «"». Иногда запускаете код, но ничего не происходит. Проверьте содержимое левого нижнего угла консоли: если там «+», это означает, что R ничего не делает, просто набрали не полное выражение, и он ждет завершения ввода. В этом случае можно начать с начала, нажав клавишу ESC, чтобы прервать обработку текущей команды.
Частая ошибка при создании графиков ggplot2 это расположение «+» в неправильном месте, он должен находиться в конце строки, а не в начале. Убедитесь, что не сделали этого случайно. Если всё ещё в тупике, попробуйте обратиться к справочной информации. Для получения развернутой справки о любой функции R достаточно ввести команду ?имя_функции в консоли, или выделить имя интересующей функции и нажать клавишу F1 в RStudio. Не волнуйтесь, если справки не кажется, бывает полезным вместо этого перейти к примерам и найти код, который соответствует тому, что пытаетесь сделать. Если и это не помогает, то внимательно перечитайте сообщение об ошибке. Иногда ответ содержится именно там. Просто для начинающих пользователей R, ответ может находиться в сообщении об ошибке, но не приходит его понимания. Еще одним отличным инструментом является Yandex, попробуйте поискать сообщение об ошибке в интернете, так как возможно, у кого-то была аналогичная проблема, и её решение описали на специализированных онлайн-форумах.
Как было показано выше, один из способов добавить дополнительные измерения на графике, это художественные вариации эстетических параметров. Но есть ещё один способ, особенно полезный для категориальных переменные, – это разбивка графика на фрагменты, подзадачи, каждая из которых заключается в отображении некоторого подмножества анализируемых данных.
Чтобы собрать свой график из нескольких фрагментов от одной одной переменной, используйте facet_wrap(). Первым аргументом функции facet_wrap() должна быть именем структуры данных в R, которое начинается с символа «~», за которым следует имя переменной. Переменная, передаваемая в функцию facet_wrap(), должна быть дискретной. Например, следующая команда:
ggplot(data = mpg) +
geom_point(mapping = aes(x = displ, y = hwy)) +
facet_wrap(~ class, nrow = 1)
разобьет общее изображение данных известной уже нам базы на фрагментарные части, расположив их одной строкой, так как указано nrow = 1:
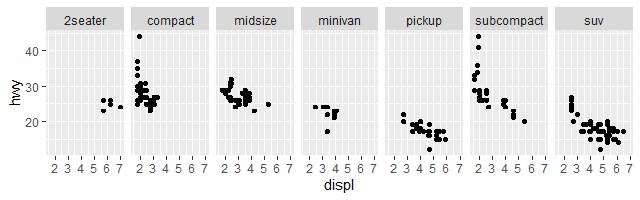
Чтобы расположить группы данных фрагментами на сетке, можно использовать комбинацию из двух переменных, добавив функцию facet_grid() к вызову графопостроителя. Первый аргумент в этом случае на этот раз будет содержать два имени переменных, разделенных знаком «~»:
ggplot(data = mpg) +
geom_point(mapping = aes(x = displ, y = hwy)) +
facet_grid(drv ~ cyl)
Если необходимо расположить группы только по одной переменной, в одну строку, либо в столбец, то достаточно поставить «.» вместо имени второй переменной. Так, например окончание +facet_grid(cyl ~ .) предпишет расположить графики вертикально, сгруппировав автомобили по числу цилиндров.
Упражнения
1. Что произойдет, если будете группировать данные по непрерывной переменной?
2. Что означают пустые ячейки на графике с facet_grid(drv~cyl)?
3. Каковы преимущества использования группирования данных частями по сравнению с цветовым выделением точек на одном графике? Каковы их недостатки? Как соблюдать баланс достоинств и недостатков этих подходов на больших объемах данных?
4. Прочитайте справку по ?facet_wrap. Что регулируется параметрами nrow, ncol? Какие ещё параметры управляют компоновкой? Почему функция facet_grid() не имеет аргументов nrow и ncol?
5. При использовании facet_grid() рекомендуется в столбцах располагать переменные с большим количеством уникальных значений. Почему?
Вернёмся к данным о результатах обучения. Во введении использовалась таблица с оценками успеваемости, которую можно воспроизвести следующей командой консоли:
My_table <– structure(list(Класс = c("7а", "7а", "7а", "7а", "7а", "7а", "7а", "7а", "7а",
"7а", "7б", "7б", "7б", "7б", "7б", "7б", "7б", "7б", "7б", "7б", "эталон", "отстающий"),
`Фимилия Имя` = c("Иванов Иван", "Петров Петр", "Сидоров Сидор", "Егоров Егор",
"Романов Роман", "Николаев Николай", "Григорьев Григогий", "Викторов Виктор",
"Михайлов Михаил", "Тимуриев Тимур", "Ульянова Ульяна", "Ольгина Ольга",
"Людмилова Людмила", "Дарьева Дарья", "Кристинина Кристина",
"Натальина Наталья", "Глафирова Глафира", "Янина Яна", "Иринова Ирина",
"Валентинова Валентина", "Идеальный ученик", "Другая крайность"), Тема1 = c(5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 5, 1), Тема2 = c(2, 3, 3, 2, 2, 3, 3, 2, 2, 3, 4, 5, 5, 4, 4, 4, 5, 5, 4, 5, 5, 1), Тема3 = c(1, 2, 2, 1, 1, 2, 2, 1, 2, 2, 1, 2, 2, 1, 1, 2, 2, 2, 1, 2, 5, 1), Тема4 = c(4, 5, 5, 4, 4, 4, 5, 5, 5, 4, 5, 5, 4, 4, 5, 5, 4, 4, 5, 4, 5, 1), `Тема 5` = c(1, 2, 2, 2, 1, 2, 1, 1, 2, 2, 1, 2, 2, 1, 1, 2, 2, 1, 2, 5, 5, 1), `№№` = c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22)),
row.names = c(NA, -22L), class = c("tbl_df", "tbl", "data.frame"))
Представим успеваемость графически:

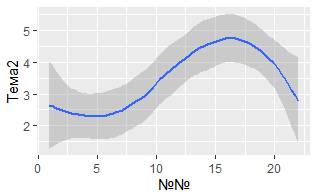
Насколько похожи эти две иллюстрации?
Оба графика содержат одну и ту же переменную x, один и тот же y, оба визуализируют одни и те же данные. Но их сюжет не идентичен. Каждая иллюстрация описается на свои визуальные образы для представления данных. В синтаксисе ggplot2 они используют разные геометрические объекты (geom). Geom – это геометрический объект, который применяет графопостроитель для представления данных. Например, линейные диаграммы используют линейные геометрические объекты, прямоугольные диаграммы используют геометрические объекты прямоугольной формы и так далее. Диаграммы рассеяния нарушают этот тренд, они используют точечное представление данных. Как видели выше, можно использовать разные геометрические объекты для визуализации одних и тех же данных. На левом графике используется точечная геометрия, а в правом – гладкая линия, усредняющая данные. Чтобы изменить геометрические примитивы на вашем чертеже, измените функцию geom_, которую добавляете к ggplot (). Например, чтобы воспроизвести вышеприведенные рисунки, выполните код:
# левый график
ggplot (data = My_table) +
geom_point (mapping = aes (x = `№№`, y = Тема2))
# правый график
ggplot (data = My_table) +
geom_smooth (mapping = aes (x = `№№`, y = Тема2))
Каждая функция geom в ggplot2 принимает аргумент mapping, однако не каждая настройка эстетики работает с любой функцией geom. Можно было бы установить форму точки, но нельзя установить форму линии. С другой стороны, можно установить параметр linetype, тогда geom_smooth() нарисует линии разного типа для каждого уникального значения переменной, которая сопоставлена с типом линии.
Например, функция geom_smooth() может разделить обучающихся по классам:
ggplot (data = My_table) +
geom_smooth (mapping = aes (x = `№№`, y = Тема2, linetype = Класс))
Одна линия описывает успехи в освоении Темы2 для всех одноклассников из «7а», а другая из «7б»:
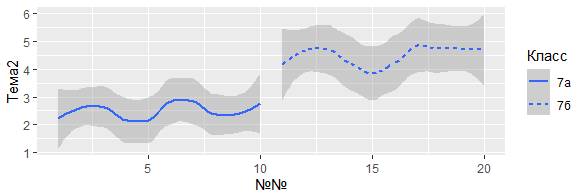
Покажется немного странным, эклектикой, но можно выполнить наложение всех линий поверх необработанных данных с последующим их окрашиванием в соответствии с успеваемостью класса. Заметим, что этот график потребует два вызова geom_ для построения, но как разместить несколько геометрических объектов разного типа на одном и том же графике.
ggplot2 обеспечивает более 40 вариантов функции geom_, пакеты расширений предоставляют ещё больше возможностей. Лучший способ получить исчерпывающий обзор, используйте справку: ?geom_smooth.
Многие варианты функции geom_, такие как geom_smooth(), например, используют один геометрический объект для отображения нескольких строк данных. Для этих функций, можно выносить эстетику группы в категориальную переменную для рисования нескольких объектов в едином стиле, так как ggplot2 нарисует отдельный объект для каждого уникального объекта значение группирующей переменной. На практике ggplot2 будет автоматическая группировка данных для этих функций всякий раз, когда сопоставляется эстетика для дискретной переменной (как было в примере с linetype). Удобно использовать эту особенность, потому что в таком случае группа эстетических параметров оказывается самой по себе, она не выносится на поле легенды или в настройки каждого объекта. К слову, показ легенды можно запретить вовсе, установкой значения параметра show.legend = FALSE, как это показано в примере кода ниже:
ggplot (data = My_table) + geom_smooth (mapping = aes (x = `№№`, y = Тема2))
ggplot (data = My_table) +
geom_smooth (mapping = aes (x = `№№`, y = Тема2, group = Класс))
ggplot (data = My_table) +
geom_smooth( mapping = aes(x = `№№`, y = Тема2, color = Класс),
show.legend = FALSE)
Чтобы изобразить несколько графиков на одном чертеже, добавьте несколько вызовов функции geom к ggplot():
ggplot (data = My_table) +
geom_point (mapping = aes (x = `№№`, y = Тема2)) +
geom_smooth (mapping = aes (x = `№№`, y = Тема2))
Это, однако, вносит некоторое дублирование в код. Представите, что хотите изменить ось y для отображения успеваемости по теме 3 вместо темы 2, нужно будет менять переменную в дух местах, при этом можно забыть про обновление в одном из них.
Дабы избежать подобного сценария, набор значений аргумента mapping передается непосредственно в функцию ggplot(). ggplot2 будет рассматривать эти значений как глобальные и применять их к каждой функции вызываемой внутри. Другими словами, следующий код создаёт ту же иллюстрацию, что и предыдущий, но более лаконичен:
ggplot (data = My_table, mapping = aes (x = `№№`, y = Тема2)) +
geom_point() + geom_smooth()
Если же размещаете параметры mapping внутри каждой функции geom, то ggplot2 будет рассматривать их как локальные настройки для слоя. Будет использоваться параметр mapping для расширения или перезаписи глобальных настроек слоя. Это позволяет настраивать различную эстетику внутри индивидуальных слоёв:
ggplot (data = My_table, mapping = aes (x = `№№`, y = Тема2)) +
geom_point (mapping = aes (color = Класс)) + geom_smooth()

Можно использовать подобную идею, чтобы выбирать разные данные для каждого слоя:
ggplot (data = My_table, mapping = aes (x = `№№`, y = Тема2)) +
geom_point (mapping = aes (color = Класс)) +
geom_smooth (data = My_table[My_table$Класс == "7а", ], se = FALSE)

В приведенном примере, гладкая линия охватывает только подмножество исходного набора данных. Локальный аргумент в geom_smooth() переопределяет глобальный аргумент отбора данных в ggplot().
Разберем как работает фильтрация чуть позже, на данный момент достаточно понять, что эта команда выбирает только учеников 7а класса, а опция se = FALSE отключает подсветку доверительного интервала.
Упражнения
1. Какую функцию из категории geom_ вы бы использовали для построения линейного графика? А для круговой, лепестковой диаграммы, гистограммы?
2. Что меняет опция show.legend = FALSE? Что происходит если её убрать? Как думаете, почему она использовалась ранее в примере?
3. Что делает аргумент se для функции geom_smooth ()?
4. Воссоздайте код R, необходимый для создания следующего рисунка и дайте ему соответствующую интерпретацию:

Подробнее остановимся на гистограммах, – так называемых прямоугольных диаграммах. Они кажутся простыми, но интересны тем, что открывают потенциальные закономерности в наблюдаемой статистике. Рассмотрим базовую линейчатую диаграмму, построенную следующим образом с помощью функции geom_bar(). Принимая во внимание, как Роберт Грин Ингерсолл (1833-1899) за оффлайн-школой закрепил хлёсткое определение: «Школа – это место, где шлифуют булыжники и губят алмазы», – медленно, но верно приобщаясь к принципиально иной онлайн-школе попробуем всё же научиться правильному обращению с алмазами. На диаграмме ниже будет показано общее количество обработанных алмазов – бриллиантов, хранящихся в предустановленной с пакетом ggplot2 базе данных, сгруппированных по огранке.
База данных о бриллиантах (diamonds) поставляется в комплекте ggplot2 и содержит информацию о ~54 000 дорогостоящих украшениях, включая цену, размер в каратах, цвет, прозрачность и огранку каждого из них. Несомненно, онлайн-учителю любой по карману. Диаграмма показывает, что бриллиантов с идеальной огранкой имеется гораздо больше, чем с черновой обработкой:
ggplot (data = diamonds) +
geom_bar (mapping = aes (x = cut, colour = diamonds$color))

На оси x диаграмма показывает огранку (cut) алмазов. На оси y с учетом цвета отображается их общее количество (count), но в базе данных не хранится поле count. Откуда же берется информация о количестве? Одни алгоритмы графопостроителей, например диаграммы рассеяния, формируют изображение по необработанным значениям исходного набора данных. Другие, например гистограммы, вычисляют новые вспомогательные значения при построении. Гистограммы, как частотные диаграммы, преобразуют ваши данные, осуществляют подсчеты числа записей определенного типа, будто раскладывая их по ящикам. При масштабировании последних диаграмма адаптируется к объему исходных данных, а затем строятся прямоугольники нужного размера. Вычисляется статистическая сводка выборки и после этого рисуется специально отформатированный прямоугольник. Алгоритм, используемый при вычислении новых значений для графиков, определяется параметром stat, сокращенно от «статистическое преобразование». В примере ниже показано, как это работает с geom_bar(). Вы можете узнать, какое статистическое преобразование использует та или иная функция, проверив значение по умолчанию аргумента stat. Например, в документации по функции ?geom_bar сказано, что её значение по умолчанию для аргумента stat это count, то есть geom_bar() использует функцию stat_count(), описанную на той же странице, что и geom_bar(), и если прокрутить вниз, то можно найти раздел «вычисляемые переменные», в котором сказано, что вычисляются две новые вспомогательные переменные: count и prop.
Как правило, префиксы geom_ и stat_ взаимозаменяемы. Например, можно запустить предыдущий пример с использованием stat_count() вместо geom_bar(). Это работает, потому что каждая функция категории geom_ имеет параметр stat по умолчанию, а каждая функция категории stat_ имеет двойственный параметр geom по умолчанию. Это означает, что можно используйте функции построения графиков, не беспокоясь о лежащих в их основе статистических преобразованиях данных. Есть три причины, по которым может потребоваться использовать параметр stat в явном виде:
1) Возможно, захотите переопределить используемое по умолчанию статистическое преобразование. В коде ниже, заменено значение аргумента stat в geom_bar() с count (принятого по умолчанию) на identity. Это позволяет сопоставить высоту баров с необработанным значением переменной. Когда говорят о столбцевой диаграмме, можно иметь ввиду такой тип гистограммы, в котором высота столбика уже присутствует в данных, либо предыдущую диаграмму, на которой высота генерируется с помощью подсчет строк.

Историческая справка.
Как известно, из всех систем оценивания знаний в России поныне жива 5-балльная, которая была в 1837 году официально установлена Министерством народного просвещения. Положим, что продемонстрированные воспитанницами на одном из уроков математики в Серпуховской женской гимназии результаты были занесены в следующую демонстрационную таблицу.
library(tidyverse)
demo <– tribble( ~оценка, ~количество,
"слабо", 1,
"посредственно", 1,
"достаточно", 3,
"хорошо", 2,
"отлично", 3 )
ggplot(data = demo) +
geom_bar(mapping = aes(x = оценка, y = количество), stat = "identity")
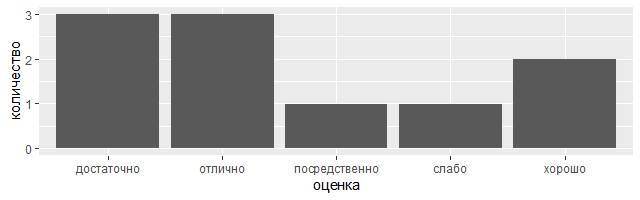
Не волнуйтесь, что не видели <– tribble раньше. Из контекста понятно назначение этих операторов, но что именно они делают в общем случае, будет подробно рассказано чуть позже.
2) Возможно, потребуется переопределить сопоставление по умолчанию от трансформированных переменных. Например, можете чтобы отобразить линейчатую диаграмму частот, а не количества:
library(tidyverse)
demo <– tribble( ~оценка, "слабо", "посредственно",
"достаточно", "достаточно", "достаточно",
"хорошо", "хорошо",
"отлично", "отлично", "отлично" )
ggplot (data = demo) +
geom_bar (mapping = aes (x = оценка, y = stat (prop), group = 1))
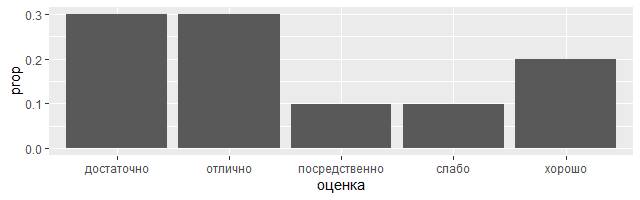
Чтобы найти полный список переменных, вычисляемых в статистике, достаточно заглянуть в раздел справки, озаглавленный как «вычисляемые переменные».
3) Возможно, захотите извлечь больше статистической информации в вашем коде. Например, если использовать функцию stat_summary(), то будет получена дополнительная описательная статистика, которую можно показать на диаграмме. Следующий фрагмент кода выберет из тестовой базы успеваемость обучающихся в 7а или 7б классах по теме 2, найдет наименьшую оценку в каждом классе, наибольшую и медианное значение. После этого найденные статистики будут отображены на диаграмме соответствующими линиями:
ggplot(data = My_table[My_table$Класс == "7а" | My_table$Класс == "7б",]) +
stat_summary(
mapping = aes(x = Класс, y = Тема2),
fun.ymin = min,
fun.ymax = max,
fun.y = median
)
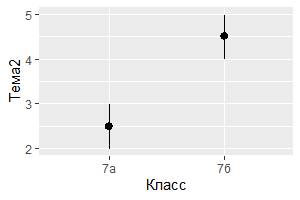
На данном этапе развития проекта, пакет ggplot2 предоставляет пользователям более 20 статистик. Каждое значение параметра stat является функцией, поэтому получить справку по ним можно обычным способом, например, введя ?stat_bin в консоли.
Упражнения
1. Что такое geom по умолчанию, связанный с stat_summary()? Как переписать код из примеров, чтобы использовать функцию начинающуюся с geom_ вместо stat_?
2. Что делает функция geom_col()? Чем она отличается от geom_bar()?
3. Большинство значений параметров geom и stat парные, и почти всегда используется вместе. Ознакомьтесь с документацией и составьте список всех пар, что у них общего?
4. Какие вспомогательные переменные вычисляет функция stat_smooth()? Какие параметры контролируют её поведение?
5. В диаграмме частот из примера установлено значение group = 1. Зачем? Другими словами, что будет нарисовано без указания этого параметра?
Есть еще одна интересная опция, связанная с гистограммами. Можно раскрасить её элементы с помощью любого цвета, указав значения параметров цвета границы (color) и заливки (fill). Обратите внимание, что произойдет, если сопоставите настройки заливки с отдельной переменной: каждый цветной прямоугольник будет представлять комбинированную информацию из двух параметров.
Регулировка положения прямоугольников задается соответствующим аргументом (position). Если его не менять, то построится столбчатая диаграмма, но можете использовать один из трех других вариантов: используемый по умолчанию (identity), развернутый по горизонтали (dodge) или с заполнением прямоугольников до равной высоты (fill). Указание position = "identity" будет размещать каждый объект ровно там, где он попадает в контекст графика. Это не очень полезно в случае детализированных прямоугольников, потому что фрагменты могут перекрываться между собой внутри одного прямоугольного столбика. Чтобы увидеть это перекрытие, можно сделать заливку полупрозрачной, придав уровню прозрачности (alpha) небольшое значение, либо использовав настройку fill = NA. Такое расположение прямоугольников полезно для 2d-примитивов, в виде точек. Указание position = "fill" работает как штабелирование, оно сделает каждый набор прямоугольников одинаковой суммарной высоты. Такой подход значительно облегчает сравнение пропорций внутри групп. И наконец position = "dodge" нарисует перекрывающиеся объекты непосредственно рядом друг с другом, что облегчает сравнение индивидуальных значений.
Заключительный тип регулировки является не очень полезным для гистограмм, но может быть очень полезен для диаграмм рассеяния. Вспомните примеры из первой главы. неужели не заметили, что график отображает только 126 точек, хотя в базе данных об автомобилях записано 234 значения. Как в известном письме на Балабановскую спичечную фабрику: «Я 11 лет считаю спички у вас в коробках – их то 59, то 60, иногда 58. Вы там сумасшедшие что ли все???». Источник обозначенной проблемы в том, что значения x и y округлены. В результате, многие точки появляясь на сетке перекрывают друг друга. Эта проблема известна как «overplotting». Такое расположение делает график трудным для понимания, когда на нём находится много данных. Распределены ли точки данных поровну на всем графике, или есть комбинация координат x и y, которая содержит 109 значений одновременно? Проблемы можно избежать, переключив регулировку положения в режим дрожания (jitter). Настройка position = "jitter" добавляет небольшое количество случайных шумов в каждую точку. Это распространяется на всю поверхность и поэтому не окажется двух точек, которые, вероятно, получат одинаковое количество случайных шумов. Добавление случайности кажется странным способом улучшения изображения, но несмотря на то, что график получится менее точным на малом масштабе, в больших масштабах график становится более иллюстративным. Поскольку это такая полезная опция, в ggplot2 внесена отдельная краткая форма записи выражения geom_point(position = "jitter"), вместо него лучше использовать geom_jitter().
Чтобы узнать больше о регулировке положения, загляните в раздел справки, посвященный каждой из перечисленных настроек.
Упражнения
1. Какие параметры функции geom_jitter() регулируют количество дрожаний?
2. Примените geom_jitter() и geom_count(), сравните полученные результаты.