
What We Cannot Know
Scientists went on to determine the chemical composition of stars we are unlikely ever to visit. As science in the nineteenth century continued to give us an ever greater understanding of the mysteries of the universe, there began to emerge a feeling that we might eventually have a complete picture.
In 1900 Lord Kelvin, regarded by many as one of the greatest scientists of his age, believed that moment had come when he declared to the meeting of the British Association of Science: ‘There is nothing new to be discovered in physics now. All that remains is more and more precise measurement.’ American physicist Albert Abraham Michelson concurred. He too thought that the future of science would simply consist of adding a few decimal places to the results already obtained. ‘The more important fundamental laws and facts of physical science have all been discovered … our future discoveries must be looked for in the sixth place of decimals.’
Five years later Einstein announced his extraordinary new conception of time and space, followed shortly after by the revelations of quantum physics. Kelvin and Michelson couldn’t have been more wrong about how much new physics there was still to discover.
What I want to try to explore is whether there are problems that we can prove will remain beyond knowledge despite any new insights. Perhaps there are none. As a scientist that is my hope. One of the dangers when faced with currently unanswerable problems is to give in too early to their unknowability. But if there are unanswerables, what status do they have? Can you choose from the possible answers and it won’t really matter which one you opt for?
Talk of known unknowns is not reserved to the world of science. The US politician Donald Rumsfeld strayed into the philosophy of knowledge with the famous declaration:
There are known knowns; there are things that we know that we know. We also know there are known unknowns; that is to say, we know there are some things we do not know. But there are also unknown unknowns, the ones we don’t know we don’t know.
Rumsfeld received a lot of stick for this cryptic response to a question fired at him during a briefing at the Department of Defense about the lack of evidence connecting the government of Iraq with weapons of mass destruction. Journalists and bloggers had a field day, culminating in Rumsfeld being given the Foot in Mouth award by the Plain English Campaign. And yet if one unpicks the statement, Rumsfeld very concisely summed up different types of knowledge. He perhaps missed one interesting category: The unknown knowns. The things that you know yet dare not admit to knowing. As the philosopher Slavoj Zizek argues, these are possibly the most dangerous, especially when held by those with political power. This is the domain of delusion. Repressed thoughts. The Freudian unconscious.
I would love to tell you about the unknown unknowns, but then they’d be known! Nassim Taleb, author of The Black Swan, believes that it is the emergence of these that are responsible for the biggest changes in society. For Kelvin it was relativity and quantum physics that turned out to be the unknown unknown that he was unable to conceive of. So in this book I can at best try to articulate the known unknowns and ask whether any will remain forever unknown. Are there questions that by their very nature will always be unanswerable, regardless of progress in knowledge?
I have called these unknowns ‘Edges’. They represent the horizon beyond which we cannot see. My journey to the Edges of knowledge to articulate the known unknowns will pass through the known knowns that demonstrate how we have travelled beyond what we previously thought were the limits of knowledge. This journey will also test my own ability to know, because it’s becoming increasingly challenging as a scientist to know even the knowns.
As much as this book is about what we cannot know, it is also important to understand what we do know and how we know it. My journey to the limits of knowledge will take me through the terrain that scientists have already mapped, to the very limits of today’s cutting-edge breakthroughs. On the way I will stop to consider those moments when scientists thought they had hit a wall beyond which progress was no longer possible, only for the next generation to find a way, and this will give us an important perspective on those problems that we might think are unknowable today. By the end of our journey I hope this book will provide a comprehensive survey not just of what we cannot know but also of the things we do know.
To help me through those areas of science that are outside my comfort zone, I have enlisted the help of experts to guide me as I reach each science’s Edge and to test whether it is my own limitations, or limitations inherent in the questions I am tackling, that make them unknowable.
What happens then if we encounter a question that cannot be answered? How does one cope with not knowing? Dare I admit to myself that some things will forever remain beyond my reach? How do we as a species cope with not knowing? That is a challenge that has elicited some interesting responses from humans across the millennia, not least the creation of an idea called God.
TRANSCENDENCE
There is another reason why I have been driven to investigate the unknowable, which is also related to my new job. The previous incumbent of the chair for the Public Understanding of Science was a certain Richard Dawkins. When I took over the position from Dawkins I braced myself for the onslaught of questions that I would get, not about science, but about religion. The publication of The God Delusion and his feisty debates with creationists resulted in Dawkins spending a lot of the later years of his tenure debating questions of religion and God.
So it was inevitable that when I took up the chair people would be interested in my stance on religion. My initial reaction was to put some distance between myself and the debate about God. My job was to promote scientific progress, and to engage the public in the breakthroughs happening around them. I was keen to move the debate back to questions of science rather than religion.
As a strategy to deflect the God questions I actually admitted that I was in fact a religious man. Before journalists got too excited, I went on to explain that my religion is the Arsenal. My temple is the Emirates (it used to be Highbury Stadium) in north London, and each Saturday I worship my idols and sing songs to them. And at the beginning of each season I reaffirm my faith that this will be the year we finally win some silverware. In an urban environment like London, football has taken over the role that religion played in society of binding a community together, providing rituals that they can share.
For me, the science that I began to learn as a teenager did a pretty good job of pushing out any vaguely religious thoughts I had had as a kid. I sang in my local church choir, which exposed me to the ideas that Christianity had to offer for understanding the universe. School education in the Seventies in the UK was infused with mildly religious overtones: renditions of ‘All Things Bright and Beautiful’ and the Lord’s Prayer in assemblies. Religion was dished up as something too simplistic to survive the sophisticated and powerful stories that I would learn in the science labs at my secondary school. Religion was quickly pushed out. Science … and football … were much more attractive.
Inevitably the questions about my stance on religion would not be fobbed off with such a flippant answer. I remember that during one radio interview on a Sunday morning on BBC Northern Ireland I was gradually sucked into considering the question of the existence of God. I guess I should have seen the warning signs. On a Sunday morning in Northern Ireland, God isn’t far from the minds of many listeners.
As a mathematician I am often faced with the challenge of proving the existence of new structures or coming up with arguments to show why such structures cannot exist. The power of the mathematical language to produce logical arguments has led a number of philosophers throughout the ages to resort to mathematics as a way of proving the existence of God. But I always have a problem with such an approach. If you are going to prove existence or otherwise in mathematics, you need a very clear definition of what it is that you are trying to prove exists.
So after some badgering by the interviewer about my stance on the existence of God, I pushed him to try to define what God meant for him so that I could engage my mathematical mind. ‘It is something which transcends human understanding.’ At first I thought: what a cop-out. You have just defined it as something which by its very nature I can’t get a handle on. But I became intrigued by this as a definition. Perhaps it wasn’t such a cop-out after all.
What if you define God as the things we cannot know. The gods in many ancient cultures were always a placeholder for the things we couldn’t explain or couldn’t understand. Our ancestors found volcanic eruptions or eclipses so mysterious that they became acts of gods. As science has explained such phenomena, these gods have retreated.
This definition has some things in common with a God commonly called the ‘God of the gaps’. This phrase was generally used as a derogatory term by religious thinkers who could see that this God was shrinking in the face of the onslaught of scientific knowledge, and a call went out to reject this kind of God. The phrase ‘God of the gaps’ was coined by the Oxford mathematician and Methodist church leader Charles Coulson, when he declared: ‘There is no “God of the gaps” to take over at those strategic places where science fails.’
But the phrase is also associated with a fallacious argument for the existence of God, one that Richard Dawkins spends some time shooting down in The God Delusion: if there are things that we can’t explain or know, there must be a God at work filling the gap. But I am more interested not in the existence of a God to fill the gap, but in equating God with the abstract idea of the things we cannot know. Not in the things we currently don’t know, but the things that by their nature we can never know. The things that will always remain transcendent.
Religion is more complex than the simple stereotype often offered up by modern society. For many ancient cultures in India, China and the Middle East, religion was not about worshipping a Supernatural Intelligence but precisely the attempt to appreciate the limits of our understanding and language. As the theologian Herbert McCabe declared: ‘To assert the existence of God is to claim that there is an unanswered question about the universe.’ Science has pushed hard at those limits. So is there anything left? Will there be anything that will always be beyond the limit. Does McCabe’s God exist?
This is the quest at the heart of this book. Can we identify questions or physical phenomena that will always remain beyond knowledge? If we can identify things that will remain in the gaps of knowledge, then what sort of God is this? What potency would such a concept have? Could the things we cannot know act in the world and affect our futures? Are they worthy of worship?
But first we need to know if in fact there is anything that will remain unanswered about the universe. Is there really anything we cannot know?
1
The unpredictable and the predetermined unfold together to make everything the way it is. It’s how nature creates itself, on every scale, the snowflake and the snowstorm. It makes me so happy. To be at the beginning again, knowing almost nothing.
Tom Stoppard, Arcadia
There is a single red dice sitting on my desk next to me. I got the dice on a trip to Las Vegas. I fell in love with it when I saw it on the craps table. It was so perfectly engineered. Such precise edges coming to a point at the corners of the cube. The faces so smooth you couldn’t feel what number the face was representing. The pips are carved out of the dice and then filled with paint that has the same density as the plastic used to make the dice. This ensures that the face representing the 6 isn’t a touch lighter than the face on the opposite side with a single pip. The feeling of the dice in the hand is incredibly satisfying. It is a thing of beauty.
And yet I hate it.
It’s got three pips pointing up at me at the moment. But if I pick it up and let it fall from my hand I have no way of knowing how it is going to land. It is the ultimate symbol of the unknowable. The future of the dice seems knowable only when it becomes the past.
I have always been extremely unsettled by things that I cannot know. Things that I cannot work out. I don’t mind not knowing something provided there is some way ultimately to calculate what’s going on. With enough time. Is this dice truly so unknowable? Or with enough information can I actually deduce its next move? Surely it’s just a matter of applying the right laws of physics and solving the appropriate mathematical equations. Surely this is something I can know.
My subject, mathematics, was invented to give people a glimpse of what’s out there coming towards us. To look into the future. To become masters of fate, not its servants. I believe that the universe runs according to laws. Understand those laws and I can know the universe. Spotting patterns has given the human species a very powerful way to take control. If there’s a pattern then I have some chance to predict the future and know the unknowable. The pattern of the Sun means I can rely on it rising in the sky tomorrow or the Moon taking 28 sunrises before it becomes full again. It is how mathematics developed. Mathematics is the science of patterns. Being able to spot patterns is a powerful tool in the evolutionary fight for survival. The caves in Lascaux show how counting 13 quarters of the Moon from the first winter rising of the Pleiades will bring you to a time in the year when the horses are pregnant and easy to hunt. Being able to predict the future is the key to survival.
But there are some things which appear to have no pattern or that have patterns that are so complex or hidden that they are beyond human knowledge. The individual roll of the dice is not like the rising of the Sun. There seems to be no way to know which of the six faces will be pointing upwards once the cube finally comes to rest. It is why the dice has been used since antiquity as a way to decide disputes, to play games, to wager money.
Is that beautiful red cube with its white dots truly unknowable? I’m certainly not the first to have a complex relationship with the dynamics of this cube.
KNOWING THE WILL OF THE GODS
On a recent trip to Israel I took my children to an archaeological dig at Beit Guvrin. It was such a popular settlement in ancient times that the site consists of layer upon layer of cities built on top of each other. There is so much stuff in the ground that the archaeologists are happy to enlist amateurs like me and my kids to help excavate the site even if a few pots get broken along the way. Sure enough, we pulled out lots of bits of pottery. But we also kept unearthing a large number of animal bones. We thought they were the remains of dinner, but our guide explained that in fact they were the earliest form of dice.
Archaeological digs of settlements dating back to Neolithic times have revealed a disproportionately high density of heel bones of sheep or other animals among the shattered pottery and flints that are usually found in sites that humans once inhabited. These bones are in fact ancestors of my casino dice. When thrown, the bones naturally land on one of four sides. Often there are letters or numbers carved into the bones. Rather than gambling, these early dice are thought to have been used for divination. And this connection between the outcome of the roll of a dice and the will of the gods is one that has persisted for centuries. Knowledge of how the dice would land was believed to be something that transcended human understanding. Its outcome was in the lap of the gods.
Increasingly these dice assumed a more prosaic place as part of our world of leisure. The first cube-shaped dice like the one on my desk were found around Harappa in what is now northeast Pakistan, where one of the first urban civilizations evolved, dating back to the third millennium BC. At the same time, you find four-faced pyramid dice appearing in a game that was discovered in the city of Ur, in ancient Mesopotamia.
The Romans and Greeks were addicts of games of dice, as were the soldiers of the medieval era who returned from the Crusades with a new game called hazard, deriving from the Arabic word for a dice: al-zahr. It was an early version of craps, the game that was being played in the casino in Vegas where I picked up my dice.
If I could predict the fall of the dice, all the games that depend on them would never have caught on. The excitement of backgammon or hazard or craps comes from not knowing how the dice are going to land. So perhaps gamers won’t thank me as I try to predict the roll of my dice.
For centuries no one even thought that such a feat was possible. The ancient Greeks, who were among the first to develop mathematics as a tool to navigate their environment, certainly didn’t have any clue how to tackle such a dynamic problem. Their mathematics was a static, rigid world of geometry, not one that could cope with the dice tumbling across the floor. They could produce formulas to describe the geometric contours of the cube, but once the dice started moving they were lost.
What about doing experiments to get a feel for the outcomes? The anti-empiricist attitude of the ancient Greeks meant they had no motivation to analyse the data and try to make a science of predicting how the dice would land. After all, the way the dice had just landed was going to have no bearing on the next throw. It was random and for the ancient Greeks that meant it was unknowable.
Aristotle believed that events in the world could essentially be classified into three categories: ‘certain events’ that happen by necessity following the laws of nature; ‘probable events’ that happen in most cases but can have a few exceptions; and finally ‘unknowable events’ that happened by pure chance. Aristotle put my dice firmly in the last category.
As Christian theology made its impact on philosophy, matters worsened. Since the throw of the dice was in the hands of God, it was not something that humans could aspire to know. As St Augustine had it: ‘We say that those causes that are said to be by chance are not non-existent but are hidden, and we attribute them to the will of the true God.’
There was no chance. No free will. The unknowable was known by God, who determined the outcome of the dice. Any attempt to try to predict the roll was the work of a heretic, someone who dared to think they could know the mind of God. King Louis XI of France even went as far as prohibiting the manufacture of dice, believing that games of chance were ungodly. But the dice like the one I have on my desk eventually began to yield their secrets. It took till the sixteenth century before dice were wrestled out of the hands of God and their fate put in the hands, and minds, of humans.
FINDING THE NUMBERS IN THE DICE
I’ve put another two dice next to my beautiful Las Vegas dice. So here’s a question: if I throw all three dice, is it better to bet on a score of 9 or a score of 10 coming up? Prior to the sixteenth century there were no tools available to answer such a question. And yet anyone who had played for long enough would know that if I was throwing only two dice then it would be wise to bet on 9 rather than 10. After all, experience would tell you before too long that on average you get 9 a third more often than you get 10. But with three dice it is harder to get a feel for which way to bet, because 9 and 10 seem to occur equally often. But is that really true?
It was in Italy at the beginning of the sixteenth century that an inveterate gambler by the name of Girolamo Cardano first realized that there are patterns that can be exploited in the throw of a dice. They weren’t patterns that could be used on an individual throw. Rather, they emerged over the long run, patterns that a gambler like Cardano, who spent many hours throwing dice, could use to his advantage. So addicted was he to the pursuit of predicting the unknowable that on one occasion he even sold his wife’s possessions to raise the funds for the table stakes.
Cardano had the clever idea of counting how many different futures the dice could have. If I throw two dice, there are 36 different futures. They are depicted in the following diagram.
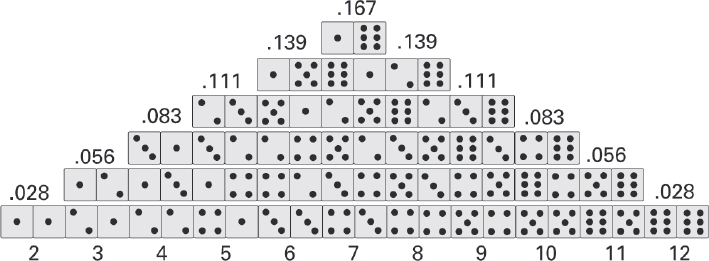
Only in three of them is the total 10, while four give you a score of 9. So Cardano reasoned that, in the case of two dice being thrown, it makes sense to bet on 9 rather than 10. It did not help in any individual game, but in the long run it meant that Cardano, if he stuck to his maths, would come out on top. Unfortunately, while a disciplined mathematician, he wasn’t very disciplined when it came to his gambling. He managed to lose all the inheritance from his father and would get into knife fights with his opponents when the dice went against him.
He was nevertheless determined to get one prophecy correct. He had apparently predicted the date of his death: 21 September 1576. To make sure he got this bet right he took matters into his own hands. He committed suicide when the date finally struck. As much as I crave knowledge, I think this is going a little far. Indeed, the idea of knowing the date of your death is something that most would prefer to opt out of. But Cardano was determined to win, even when he was dicing with Death.
Before taking his life, he wrote what many regard as the first book that made inroads into predicting the behaviour of the dice as it rolls across the table. Although written around 1564, Liber de Ludo Aleae didn’t see the light of day until it was eventually published in 1663.
It was in fact the great Italian physicist Galileo Galilei who applied the same analysis that Cardano had described to decide whether to bet on a score of 9 or 10 when three dice are thrown. He reasoned that there are 6 × 6 × 6 = 216 different futures the dice could take. Of these, 25 gave you a 9 while 27 gave you a 10. Not a big difference, and one that would be difficult to pick up from empirical data, but large enough that betting on 10 should give you an edge in the long run.
AN INTERRUPTED GAME
The mathematical mastery of the dice shifted from Italy to France in the mid-seventeenth century when two big hitters, Blaise Pascal and Pierre de Fermat, started applying their minds to predicting the future of these tumbling cubes. Pascal had become interested in trying to understand the roll of the dice after meeting one of the great gamblers of the day, Chevalier de Méré. De Méré had challenged Pascal with a number of interesting scenarios. One was the problem Galileo had cracked. But the others included whether it was advisable to bet that at least one 6 will appear if a dice is thrown four times, and also the now famous problem of ‘points’.
Pascal entered into a lively correspondence with the great mathematician and lawyer Pierre de Fermat in which they tried to sort out the problems set by de Méré. With the throw of four dice, one could consider the 6 × 6 × 6 × 6 = 1296 different outcomes and count how many include a 6, but that becomes pretty cumbersome.