
What We Cannot Know
Born a hundred years after Laplace, Poincaré believed, like his compatriot, in a clockwork universe, a universe governed by mathematical laws and utterly predictable. ‘If we know exactly the laws of nature and the situation of the universe at the initial moment, we can predict exactly the situation of the same universe at a succeeding moment.’
Understanding the world was Poincaré’s prime motivation for doing mathematics. ‘The mathematical facts worthy of being studied are those which, by their analogy with other facts, are capable of leading us to the knowledge of a physical law.’
Although Newton’s laws of motion had spawned an array of mathematical equations to describe the evolution of the physical world, most of them were still extremely complicated to solve. Take the equations for a gas. Think of the gas as made up of molecules crashing around like tiny billiard balls, and theoretically the future behaviour of the gas was bound up in Newton’s laws of motion. But the sheer number of balls meant that any exact solution was well beyond reach. Statistical or probabilistic methods were still by far the best tool to understand the behaviour of billions of molecules.
There was one situation where the number of billiard balls was reasonably small and a solution seemed tractable. The solar system. Poincaré became obsessed with the question of predicting what lay in store for our planets as they danced their way into the future.
Because the gravitational pull of a planet on another planet at some distance from the first planet is the same as if all the mass of the planet is concentrated at its centre of gravity, to determine the ultimate fate of the solar system one can consider planets as if they are just points in space, as Newton had done. This means that the evolution of the solar system can be described by three coordinates for each planet that locate the centre of mass in space together with three additional numbers recording the speed in each of the three dimensions of space. The forces acting on the planets are given by the gravitational forces exerted by each of the other planets. With all this information one just needs to apply Newton’s second law to map out the course of the planets into the distant future.
The only trouble is that the maths is still extremely tricky to work out. Newton had solved the behaviour of two planets (or a planet and a sun). They would follow elliptical paths, with their common focal point being the common centre of gravity. This would repeat itself periodically to the end of time. But Newton was stumped when he introduced a third planet. Trying to calculate the behaviour of a solar system consisting, say, of the Sun, the Earth and the Moon seemed simple enough, but already you are facing an equation in 18 variables: 9 for position and 9 for the speed of each planet. Newton conceded that ‘to consider simultaneously all these causes of motion and to define these motions by exact laws admitting of easy calculation exceeds, if I am not mistaken, the force of any human mind’.
The problem got a boost when King Oscar II of Norway and Sweden decided to mark his sixtieth birthday by offering a prize for solving a problem in mathematics. There are not many monarchs around the world who would choose maths problems as their way to celebrate their birthdays, but Oscar had always enjoyed the subject ever since he had excelled at it when he was a student at Uppsala University.
His majesty Oscar II, wishing to give a fresh proof of his interest in the advancement of mathematical science has resolved to award a prize on January 21, 1889, to an important discovery in the field of higher mathematical analysis. The prize will consist of a gold medal of the eighteenth size bearing his majesty’s image and having a value of a thousand francs, together with the sum of two thousand five hundred crowns.
Three eminent mathematicians convened to choose a number of suitable mathematical challenges and to judge the entries. One of the questions they posed was to establish mathematically whether the solar system was stable. Would it continue turning like clockwork, or, at some point in the future, might the Earth spiral off into space and disappear from our solar system?
To answer the question required solving the equations that had stumped Newton. Poincaré believed that he had the skills to win the prize. One of the common tricks used by mathematicians is to attempt a simplified version of the problem first to see if that is tractable. So Poincaré started with the problem of three bodies. This was still far too difficult, so he decided to simplify the problem further. Instead of the Sun, Earth and Moon, why not try to understand two planets and a speck of dust? The two planets won’t be affected by the dust particle, so he could assume, thanks to Newton’s solution, that they just repeated ellipses round each other. The speck of dust, on the other hand, would experience the gravitational force of the two planets. Poincaré set about trying to describe the path traced by the speck of dust. Some understanding of this trajectory would form an interesting contribution to the problem.
Although he couldn’t crack the problem completely, the paper he submitted was more than good enough to secure King Oscar’s prize. He’d managed to prove the existence of an interesting class of paths that would repeat themselves, so-called periodic paths. Periodic orbits were by their nature stable because they would repeat themselves over and over, like the ellipses that two planets would be guaranteed to execute.
The French authorities were very excited that the award had gone to one of their own. The nineteenth century had seen Germany steal a march on French mathematics, so the French academicians excitedly heralded Poincaré’s win as proof of a resurgence of French mathematics. Gaston Darboux, the permanent secretary of the French Academy of Sciences, declared:
From that moment on the name of Henri Poincaré became known to the public, who then became accustomed to regarding our colleague no longer as a mathematician of particular promise but as a great scholar of whom France has the right to be proud.
A SMALL MISTAKE WITH BIG IMPLICATIONS
Preparations began to publish Poincaré’s solution in a special edition of the Royal Swedish Academy of Science’s journal Acta Mathematica. Then came the moment every mathematician dreads. Every mathematician’s worst nightmare. Poincaré thought his work was safe. He’d checked every step in the proof. Just before publication, one of the editors of the journal raised a question over one of the steps in his mathematical argument.
Poincaré had assumed that a small change in the positions of the planets, a little rounding up or down here or there, was acceptable as it would result in only a small change in their predicted orbits. It seemed a fair assumption. But there was no justification given for why this would be so. And in a mathematical proof, every step, every assumption, must be backed up by rigorous mathematical logic.
The editor wrote to Poincaré for some clarification on this gap in the proof. But as Poincaré tried to justify this step, he realized he’d made a serious mistake. He wrote to Gösta Mittag-Leffler, the head of the prize committee, hoping to limit the damage to his reputation:
The consequences of this error are more serious than I first thought. I will not conceal from you the distress this discovery has caused me … I do not know if you will still think that the results which remain deserve the great reward you have given them. (In any case, I can do no more than to confess my confusion to a friend as loyal as you.) I will write to you at length when I can see things more clearly.
Mittag-Leffler decided he needed to inform the other judges:
Poincaré’s memoir is of such a rare depth and power of invention, it will certainly open up a new scientific era from the point of view of analysis and its consequences for astronomy. But greatly extended explanations will be necessary and at the moment I am asking the distinguished author to enlighten me on several important points.
As Poincaré struggled away he soon saw that he was simply mistaken. Even a small change in the initial conditions could result in wildly different orbits. He couldn’t make the approximation that he’d proposed. His assumption was wrong.
Poincaré telegraphed Mittag-Leffler to break the bad news and tried to stop the paper from being printed. Embarrassed, he wrote:
It may happen that small differences in the initial conditions produce very great ones in the final phenomena. A small error in the former will produce an enormous error in the latter. Prediction becomes impossible.
Mittag-Leffler was ‘extremely perplexed’ to hear the news.
It is not that I doubt that your memoir will be in any case regarded as a work of genius by the majority of geometers and that it will be the departure point for all future efforts in celestial mechanics. Don’t therefore think that I regret the prize … But here is the worst of it. Your letter arrived too late and the memoir has already been distributed.
Mittag-Leffler’s reputation was on the line for not having picked up the error before they’d publicly awarded Poincaré the prize. This was not the way to celebrate his monarch’s birthday! ‘Please don’t say a word of this lamentable story to anyone. I’ll give you all the details tomorrow.’
The next few weeks were spent trying to retrieve the printed copies without raising suspicion. Mittag-Leffler suggested that Poincaré should pay for the printing of the original version. Poincaré, who was mortified, agreed, even though the bill came to over 3500 crowns, 1000 crowns more than the prize he’d originally won.
In an attempt to rectify the situation, Poincaré set about trying to sort out his mistake, to understand where and why he had gone wrong. In 1890, Poincaré wrote a second, extended paper explaining his belief that very small changes could cause an apparently stable system suddenly to fly apart.
What Poincaré discovered, thanks to his error, led to one of the most important mathematical concepts of the last century: chaos. It was a discovery that places huge limits on what we humans can know. I may have written down all the equations for my dice, but what if my dice behaves like the planets in the solar system? According to Poincaré’s discovery, if I make just one small error in recording the starting location of the dice, that error could expand into a large difference in the outcome of the dice by the time it comes to rest on the table. So is the future of my Vegas dice shrouded behind the mathematics of chaos?
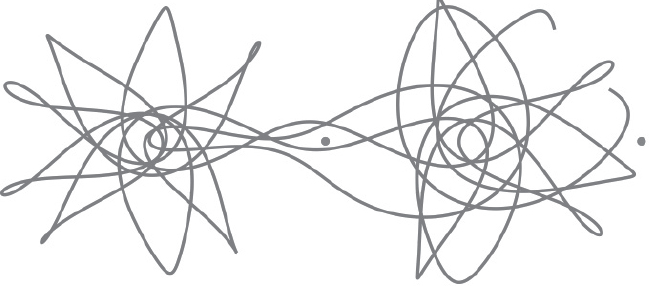
The chaotic path mapped out by a single planet orbiting two suns.
2
If nature were not beautiful it would not be worth knowing, and if nature were not worth knowing, life would not be worth living.
Henri Poincaré
I wasted a lot of time at university playing billiards in our student common room. I could have pretended that it was all part of my research into angles and stuff, but the truth is that I was procrastinating. It was a good way of putting off having to cope with not being able to answer that week’s set of problems. But in fact the billiard table hides a lot of interesting mathematics in its contours. Mathematics that is highly relevant to my desire to understand my dice.
If I shoot a ball round a billiard table and mark its path, then follow that by shooting another ball off in very nearly the same direction, the second ball will trace out a very similar path to the first ball. Poincaré had believed that the same principle applied to the solar system. Fire a planet off in a slightly different direction then the solar system will evolve in a very similar pattern. This is most people’s intuition: if I make a small change in the initial conditions of the planet’s trajectory it won’t alter the course of the planet much. But the solar system seems to be playing a slightly more interesting game of billiards than the one I played as a student.
Rather surprisingly, if I change the shape of the billiard table this intuition turns out to be wrong. For example, fire balls round a billiard table shaped like a stadium with semicircular ends but straight sides and the paths can diverge dramatically even though they started in almost the same direction. This is the signature of chaos: sensitivity to very small changes in the initial conditions.
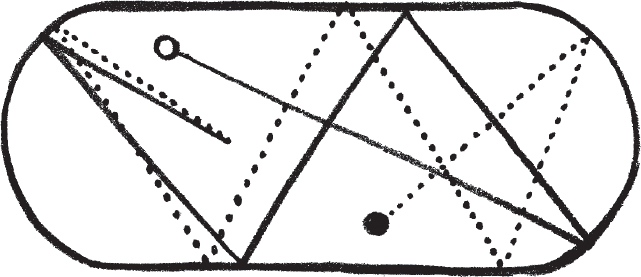
Two quickly diverging paths taken by a billiard ball round a stadium-shaped billiard table.
So the challenge for me is to determine whether the fall of my dice is predictable, like a conventional game of billiards, or whether the dice is playing a game of chaotic billiards.
THE DEVIL IN THE DECIMALS
Despite Poincaré being credited as the father of chaos, it is striking that this sensitivity of many dynamical systems to small changes was not very well known for decades into the twentieth century. Indeed, it really took the rediscovery of the phenomenon by scientist Edward Lorenz, when he, like Poincaré, thought he’d made some mistake, before the ideas of chaos became more widely known.
While working as a meteorologist at MIT in 1963, Lorenz had been running equations for the change of temperature in a dynamic fluid on his computer when he decided he needed to rerun one of his models for longer. So he took some of the data that had been output earlier in the run and re-entered it, expecting to be able to restart the model from that point.
When he returned from coffee, he discovered to his dismay that the computer hadn’t reproduced the previous data but had generated very quickly a wildly divergent prediction for the change in temperature. At first he couldn’t understand what was happening. If you input the same numbers into an equation, you don’t expect to get a different answer at the other end. It took him a while to realize what was going on: he hadn’t input the same numbers. The computer printout of the data he’d used had only printed the numbers to three decimal places, while it had been calculating using the numbers to six decimal places.
Even though the numbers were actually different, they differed only in the fourth decimal place. You wouldn’t expect it to make that big a difference, but Lorenz was struck by the impact such a small difference in the numbers had on the resulting data. Here are two graphs created using the same equation but where the data that is put into the equations differ very slightly. One graph uses the input data 0.506127. The second graph approximates this to 0.506. Although the graphs start out following similar paths, they very quickly behave completely differently.

The model that Lorenz was running was a simplification of models for the weather that analysed how the flow of air behaves when subjected to differences in temperature. His rediscovery of how small changes in the way you start a system can have such a big impact on the outcome would have huge implications for our attempts to use mathematical equations to make predictions into the future. As Lorenz wrote:
Two states that were imperceptibly different could evolve to two considerably different states. Any error in the observation of the present state – and in a real system, this appears to be inevitable – may render an acceptable prediction of the state in the distant future impossible.
THE REVENGE OF THE GRASSHOPPER
When Lorenz explained his findings to a colleague, he received the reply: ‘Edward, if your theory is correct, one flap of a seagull’s wings could alter the course of history forever.’
The seagull would eventually be replaced by the now famous butterfly when Lorenz presented his findings in 1972 at the American Association for the Advancement of Science in a paper entitled: ‘Does the Flap of a Butterfly’s Wings in Brazil Set Off a Tornado in Texas?’
Curiously, both the seagull and the butterfly might have been pre-empted by the grasshopper. It seems that already in 1898 Professor W. S. Franklin had realized the devastating effect that the insect community could have on the weather. Writing in a book review, he believed:
An infinitesimal cause may produce a finite effect. Long-range detailed weather prediction is therefore impossible, and the only detailed prediction which is possible is the inference of the ultimate trend and character of a storm from observations of its early stages; and the accuracy of this prediction is subject to the condition that the flight of a grasshopper in Montana may turn a storm aside from Philadelphia to New York!
This is an extraordinary position to be in. The equations that science has discovered give me a completely deterministic description of the evolution of many dynamical systems like the weather. And yet in many cases I am denied access to the predictions that they might make because any measurement of the location or wind speed of a particle is inevitably going to be an approximation to the true conditions.
This is why the MET office, when it is making weather predictions, takes the data recorded by the weather stations dotted across the country and then, instead of running the equations on this data, the meteorologists do several thousand runs, varying the data over a range of values. The predictions stay close for a while, but by about five days into the future the results have often diverged so wildly that one set of data predicts a heat wave to hit the UK while a few changes in the decimal places of the data result in rain drenching the country.

Starting from nearly the same conditions, forecast A predicts strong wind and rain over the British Isles in 4 days’ time, while forecast B predicts incoming high pressure from the Atlantic.
The great Scottish scientist James Clerk Maxwell articulated the important difference between a system being deterministic yet unknowable in his book Matter and Motion, published in 1877: ‘There is a maxim which is often quoted, that “The same causes will always produce the same effects.”’ This is certainly true of a mathematical equation describing a dynamical system. Feed the same numbers into the equation and you won’t get any surprises. But Maxwell continues: ‘There is another maxim which must not be confounded with this, which asserts that “Like causes produce like effects.” This is only true when small variations in the initial circumstances produce only small variations in the final state of the system.’ It is this maxim that the discovery of chaos theory in the twentieth century revealed as false.
This sensitivity to small changes in initial conditions has the potential to sabotage my attempts to use the equations I’ve written down to predict the outcome of my dice. I’ve got the equations, but can I really be sure that I’ve accurately recorded the angle at which the cube leaves my hand, the speed at which it is spinning, the distance to the table?
Of course, everything isn’t completely hopeless. There are times when small changes don’t alter the course of the equations dramatically, like the paths in the classical billiard table. What is important is to know when you cannot know. A beautiful example of knowing the point when you can’t know what is going to happen next was discovered by mathematician Robert May when he analysed the equations for population growth.
KNOWING WHEN YOU CAN’T KNOW
Born in Australia in 1938, May had originally trained as a physicist working on superconductivity. But his academic work took a dramatic turn when he was exposed in the late 1960s to the newly formed movement in social responsibility in science. His attention shifted from the behaviour of collections of electrons to the more pressing questions of the behaviour of population dynamics in animals. Biology at the time was not a natural environment for the mathematically minded, but following May’s work that would all change. It was this fusion of the hardcore mathematical training he’d received as a physicist combined with a new sensibility to biological issues that led to his great breakthrough.
In a paper in Nature called ‘Simple Mathematical Models with Very Complicated Dynamics’, published in 1976, May explored the dynamics of a mathematical equation describing population growth from one season to the next. He revealed how even a quite innocent equation can produce extraordinarily complex behaviour in the numbers. His equation for population dynamics wasn’t some complicated differential equation but a simple discrete feedback equation that anyone with a calculator can explore.
Feedback equation for population dynamics
Suppose I consider an animal population whose numbers can vary between 0 and some hypothetical maximum value that I will call N. Given some fraction Y (lying between 0 and 1) of that maximum, the equation determines what in the next season is the revised fraction of the population that survives after reproduction and competition for food. Let’s suppose that each season the reproduction rate is given by a number r. So that if the fraction of the maximum population that survived to the end of the season was Y, the next generation swells to r × Y × N.
But not all of these new animals will survive. The equation determines that the fraction that will not survive is also given by Y. So out of the r × Y × N animals that start the season, Y × (r × Y × N) die. So the total left at the end of the season is (r × Y × N) – (r × Y2 × N) = [r × Y × (1 – Y)] × N, which means that the fraction of the maximum population that exists in the current season is r × Y × (1 – Y).
Essentially the model assumes that at the end of each season the surviving population gets multiplied by a constant factor, called r, the reproduction rate, to produce the number of animals at the beginning of the next season. But there aren’t enough resources for them all to survive. The equation then calculates how many of these animals will make it till the end of the season. The resulting number of animals that survive then gets multiplied by the factor r again for the next generation. The fascinating property of this equation is that its behaviour really depends only on the choice of r, the reproduction rate. Some choices of r lead to extremely predictable behaviours. I can know exactly how the numbers will evolve. But there is a threshold beyond which I lose control. Knowledge is no longer within reach because the addition of one extra animal into the mix can result in dramatically different population dynamics.
For example, May discovered that if r lies between 1 and 3 then the population eventually stabilizes. In this case it doesn’t matter what the initial conditions are, the numbers will gradually tend to a fixed value depending on r. It’s like playing billiards on a table where there is a sinkhole in the middle. However I shoot the ball off, it eventually finds its way to the bottom of the sinkhole.