What We Cannot Know

ZOOMING IN

To predict how the dice might land I need to know what my cube is made from. Denser acetate in one corner of the shape will lead to one side of the dice being favoured over the others. So if I am going to attempt to apply Newton’s laws to my dice as it tumbles through the air, I need to know how my dice is put together. Is it a continuous structure, or, if I look closely, is it made up of discrete pieces?

If I accept the limits of my own vision, as Schopenhauer’s quote at the beginning of this Edge suggests I tend to, then I can’t see anything other than the clear red acetate that makes up the dice. But with an optical microscope I can magnify the dice by a factor of 1500, which would scale my dice up to the size of a large building. Peering inside this huge dice still won’t reveal much about the secrets of how it is built. Everything still looks pretty smooth and continuous.

In the twentieth century microscopes exploiting different bits of the electromagnetic spectrum have allowed scientists to create images which magnify things a further 1000 times. Now my dice will span from one side of London to the other. At this magnification the dice is looking grainier. The sense of the continuous structure is giving way to something more discrete. Current electron microscopes allow me to zoom in another 10 times closer, at which point I might start to see the carbon and oxygen atoms that I know are some of the ingredients of the acetate from which my dice is made.

The intriguing thing is that scientists had already formulated an atomic view of matter long before I could actually see these atoms under the modern microscopes in the labs across the road from the mathematics department. And it is a combination of a mathematical and theoretical perspective with a physical vision that is the best tool for knowing what my dice is made from.

But atoms like oxygen and carbon turned out not to be as atomic as the name suggests. Beyond the atomic structure revealed by current electron microscopes, I know that there is more internal structure. Atoms give way to electrons, protons and neutrons. Protons and neutrons in turn give way to quarks. In 2013 quantum microscopes even captured pictures of electrons orbiting the nucleus of a hydrogen atom. But is there a theoretical limit to how far I can dig down inside my dice?

What happens, for example, if I take my dice and keep dividing it in half? Just how far can I go? The mathematical side of me says: no problem. If I have a number I can keep dividing it by two:

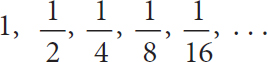
There is no point mathematically where I have to stop. Yet if I start trying to do the same thing with the physical dice sitting on my desk and cut it in half, then in half again, just how far can I keep going?

The tension between the continuous versus the discrete nature of matter, between what is possible mathematically versus the limits placed by physical reality, has been raging for millennia. Is the universe dancing to the sound of my trumpet or shimmying to the glissando of my cello?

THE MUSIC OF THE SPHERES

How did I personally come to know about these electrons and quarks that are believed to be the last layer of my dice? I’ve never seen them. If I actually ask myself how I know about them, the answer is that I’ve been told and read about them so many times that I’ve actually forgotten why or how I know. Or, come to think of it, was I ever told how we know? Is it a bit like the way I know Everest is the tallest mountain? I know that only because I’ve been told it enough times. So before I ask whether there is anything beyond this layer, I need to know how we got to these building blocks.

Reading through the history, I am surprised that it is only just over a hundred years ago that convincing evidence was provided for the fact that things like my dice are made of discrete building blocks called atoms and are not just continuous structures. Despite being such a relatively recent discovery, the hunch that this was the case goes back thousands of years. In India it was believed that matter was made from basic atoms corresponding to taste, smell, colour and touch. They divided atoms into ones that were infinitesimally small and took up no space, and others that were ‘gross’ and took up finite space – an extremely prescient theory, as you will see once I explain our current model of matter.

In the West it was the ancient Greeks who first proposed an atomistic philosophy of nature, advocating the reductionist view that physical reality could be reduced to fundamental units that made up all matter. These atoms could not be broken down into anything smaller, and their properties should not depend on some further complex inner structure. One of the seeds for this belief in a universe made from indivisible building blocks was the Pythagorean philosophy that number is at the heart of explaining the secrets of the universe.

The conviction in the power of whole numbers had its origins in a rather remarkable discovery attributed to Pythagoras: namely, that number is the basis of the musical harmony that both my cello and my trumpet exploit. The story has it that inspiration struck when he passed a blacksmith and heard the hammers banging out a combination of harmonious notes. (We can’t be sure whether this and similar stories told about Pythagoras are true, or even whether he really existed and wasn’t an invention of later generations used to promote new ideas.)

This story goes that he went home and experimented with the notes made by a stringed instrument. If I take the vibrating string on my cello then I can produce a continuous sequence of notes by gradually pushing my finger up towards the bridge of the cello, making a sound called a glissando (although the question of whether this is truly producing a continuous sequence of notes will be challenged in the next Edge). If I stop at the positions that produce notes that sound harmonious when combined with the open vibrating string, it turns out that the lengths of the strings are in a perfect whole-number ratio with each other.

For example, if I place my finger at the halfway point along the vibrating string I get a note which sounds almost like the note I started with. The interval is called the octave, and to the human ear the note sounds so similar to the note on the open string that in the musical notation that emerged we give these notes the same names. If I place my finger a third of the distance from the head of the cello, I get a note which sounds particularly harmonious when combined with the note of the open string. Known as the perfect fifth, what our brains are responding to is a subliminal recognition of this whole-number relationship between the wavelengths of the two notes.

Having found that whole numbers were at the heart of harmony, the Pythagoreans began to build a model of the universe that had these whole numbers as the fundamental building blocks of everything they saw or heard around them. Greek cosmology was dominated by the idea of a mathematical harmony in the skies. The orbits of the planets were believed to be in a perfect mathematical relationship to each other, giving rise to the idea of the music of the spheres.

More importantly for understanding the make-up of my dice, it was also believed that discrete numbers rather than a continuous glissando were the key to understanding what constituted matter. The Pythagoreans proposed the idea of fundamental atoms that, like numbers, could be added together to get new matter. The Greek philosopher and mathematician Plato developed the Pythagorean philosophy and makes these atoms into discrete pieces of geometry.

Plato believed the atoms were actually bits of mathematics: triangles and squares. These were the building blocks for the shapes that he believed were the key to the ingredients of Greek chemistry: the elements of fire, earth, air and water. Each element, Plato believed, had its own three-dimensional mathematical shape.

Fire was the shape of a triangular-based pyramid, or tetrahedron, made from 4 equilateral triangles. Earth was cube-shaped like my Vegas dice. Air was made from a shape called an octahedron, constructed from 8 equilateral triangles. It is a shape that looks like two square-based pyramids fused together along the square faces. Finally, water corresponded to the icosahedron, a shape made from 20 equilateral triangles. Plato believed that it was the geometrical interaction of these basic shapes that gave rise to the chemistry of the elements.

The atomistic view of matter was not universally held across the ancient world. After all, there was no evidence for these indivisible bits. You couldn’t see them. Aristotle was one of those who did not believe in the idea of fundamental atoms. He thought that the elements were continuous in nature, that you could theoretically keep dividing my dice up into smaller and smaller pieces. He believed that fire, earth, air and water were elemental in the sense that they could not be divided into ‘bodies different in form’. If you kept dividing, you would still get water or air. If you take a glass of water then to the human eye, it appears to be a continuous structure which can theoretically be infinitely divided. If I take a piece of rubber then I can stretch it in a smooth manner making it appear continuous in nature. The stage was set for the battle between the continuous and discrete models of matter. The glissando versus the discrete notes of the musical scale. The cello versus the trumpet.

Intriguingly, it was a discovery credited to the Pythagoreans that would threaten the atomistic view and which turned the tide for many years in favour of the belief that matter could be divided infinitely.

NUMBERS AT THE EDGE

From the atomistic point of view, if I draw two lines on the page then each line will be made from a certain number of these indivisible atoms and hence their lengths would be in a ratio of whole numbers corresponding to the number of atoms making up each line. But things didn’t turn out to be so orderly. In fact, it was Pythagoras’ own theorem about right-angled triangles that revealed that the world of geometry could give rise to lines whose relative lengths could not be captured by simple fractions.

The dimensions of my dice already have hidden in them a challenge to this atomistic view of nature. Take two of the edges of the cube at 90 degrees to each other. They have equal length. Now consider the diagonal line across the face of the cube that completes the triangle made up from the two edges of equal length. How long is this diagonal line relative to the shorter sides?

Pythagoras’ theorem about right-angled triangles says that the square of the length of the diagonal is equal to the sum of the squares of the lengths of the two shorter sides. If I set the length of the sides of my dice as 1, then Pythagoras’ theorem implies that the length of the diagonal across the face of my dice is a number which, when you square it, is equal to 2. So what is this number?

The Babylonians had been fascinated by the challenge of calculating this length. Dating back to the Old Babylonian period (1800–1600 BC), a tablet housed at Yale University has an estimate for the distance. Written using the sexagesimal system, or base 60, they got the length to be:

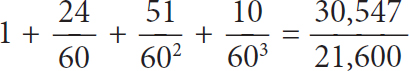
which in decimal notation comes out at 1.41421296296 …, where the 296 repeats itself infinitely often. It is true of all fractions that when written as decimals they repeat themselves after some point. Indeed, any decimal expansion which does repeat itself can always be written as a fraction. The Babylonian calculation is quite a feat. It is correct to six decimal places. But when you square that fraction it just misses being 2. What the ancient Greeks discovered is that however hard the Babylonian scribes tried, they would always find that their fractions just missed squaring to 2.

It was one of Pythagoras’ followers, Hippasus, who is credited with the discovery that the Babylonians were doomed to failure. He proved that the length of this diagonal across the side of my dice could never be expressed as a fraction.

Pythagoras’ theorem about right-angled triangles implied that this long side had length the square root of 2 times the length of the short sides. But Hippasus could prove that there was no fraction whose square was exactly 2. The proof uses one of the classic tools in the mathematician’s arsenal: proof by contradiction. Hippasus began by assuming there was a fraction whose square was 2. By some deft manipulation this always led to the contradictory statement that there was a number that was both odd and even. The only way to resolve this contradiction was to realize that the original assumption must have been false: there can be no fraction whose square is 2.

His fellow Pythagoreans were reputed to be dismayed by the revelation that their beautiful right-angled triangles could produce such inharmonic lengths. The sect took a vow of silence, but when Hippasus let the discovery out of the bag, the story goes that he was drowned at sea for revealing such disharmony in the physical world. But these new numbers, called irrational numbers because they are not ratios of whole numbers, were not so easily silenced.

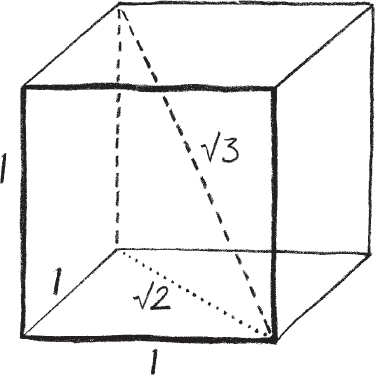
Irrational lengths inside the cube.

I certainly have the feeling that this length exists. I can see it on a ruler held up against the long side of the triangle. It is the distance between two opposite corners of any side of my dice. Yet try to write down the number as an infinite decimal and I can never capture it. It begins 1.414213562 … and then continues to infinity never repeating itself.

IRRATIONAL EXUBERANCE

The discovery by the ancient Greeks that there were lengths that couldn’t be expressed as simple ratios of whole numbers led the mathematicians of the time to create new mathematics, the mathematics of irrational numbers, in order to truly take the measure of the universe. Other basic lengths like π, the circumference of a circle of unit diameter, also turned out to be irrational and not captured by ratios of whole numbers. Although the ancient Greeks knew 2000 years ago about the irrationality of the square root of 2, it took till the eighteenth century for Swiss mathematician Johann Heinrich Lambert to prove that no fraction could capture π.

Despite my aversion to things we cannot know, reading about numbers that can’t be captured using simple whole-number ratios or fractions was one of the defining moments that sparked my love affair with mathematics. The same year that my music teacher introduced me to the trumpet in the storeroom cupboard, my maths teacher introduced me to the proof of the irrationality of the square root of 2. The proof was contained in one of the books my maths teacher recommended to me to ignite the mathematical fire in me. It worked. I was amazed to find that you could prove with a finite logical argument that only the infinite could articulate what a length such as the diagonal across a square measured. If I couldn’t write out this length, the next best thing was knowing why I couldn’t know this number.

Since reading that proof as a schoolkid I have learnt about alternative ways to explore these irrational numbers – so perhaps these are numbers we can know. There are infinite expressions with patterns that make the number less mysterious. For example,

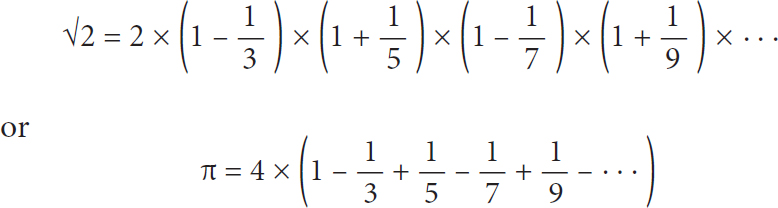
The discovery of these expressions pulls these irrational numbers into the known. A fraction is a number whose decimal expansion repeats itself from some point. Couldn’t I regard these expressions as a pattern, not too dissimilar from the repeating pattern of the decimal expansion of the fraction? The repeating pattern of the fraction means that there are two numbers whose ratio captures the number, while in the case of √2 and π I am resigned to needing infinitely many numbers to pin down these lengths. The question of whether something has to be finite to be known will haunt me continually throughout my journey to the frontiers of the unknown.

Of course, for any practical application of these numbers, I could probably get away with an approximation which is a fraction. Most engineers are happy to use the estimate 22⁄7 for π that Archimedes got by approximating a circle with a 96-sided figure. In fact, I need only know 39 digits of π to be able to calculate the circumference of a circle the size of the observable universe to a precision comparable to the size of a hydrogen atom. There even exists a formula that can tell me what the millionth digit of π is without calculating all the intervening digits. Not something that I’m desperate to know. But this formula will only ever give me finite knowledge of a number that necessitates the infinite to fully embrace it.

The discovery of these numbers seemed to imply an infinite divisibility of space. Only by dividing space infinitely would I be able to measure the precise dimensions of my simple cube. The discovery meant that in the West Aristotle’s continuous view of matter would remain dominant until the Renaissance.

THE HARMONY OF TINY SPHERES

With the insights of the science of Newton’s generation and beyond, the tide would turn in favour of the view that the universe is indeed made from basic building blocks. Newton’s contemporary, Robert Boyle, was perhaps the first to question the Aristotelian view of matter, which had dominated for nearly 2000 years. In his book The Sceptical Chymist, Boyle challenged the idea that matter was made up of the four elements of fire, earth, air and water. These might be good descriptions of the states of matter but not of the constituents.

Instead, he argued for a new list of chemical elements. Not only that, he made what at the time was rather a heretical statement. He believed that these elements would be minute bodies or atoms differing only in ‘bulk, figure, texture and motion’. This was regarded as theologically dangerous: a materialistic godless view of the world in the eyes of the Church, which had always favoured the Aristotelian view. Some have declared Boyle the Galileo of the chemical revolution.

Although Newton would concur with Boyle’s proposal for a material world made from indivisible units, the mathematical tools that Newton developed at the same time as Boyle’s work relied heavily on time and space being infinitely divisible. The calculus that allowed one to take a snapshot of a universe in constant flux made sense only as a process in which space is divided up into ever smaller pieces and then interpreting what happens in the limit as the pieces become infinitesimally small.

The question of the infinite divisibility of time and space had fuelled philosophical argument since the ancient Greek thinker Zeno of Elea came up with paradoxes that seemed to arise from this cutting up of space. For example, Zeno proposed that an arrow can never hit its target because it must first cover half the distance to the target, then half the distance again, and then half again, requiring infinitely many moves if it is ever going to make it to the target. The success of Newton’s calculus reignited the debate. There were still those who considered such infinite divisibility as almost heretical.

Bishop Berkeley dedicated a whole treatise called The Analyst to arguing that trying to make sense of dividing by zero was absurd, which the subtitle made clear: it was ‘Addressed to an Infidel MATHEMATICIAN’.

While most infidel mathematicians quickly latched on to the power of the calculus, Newton’s other breakthroughs supported a view that, although space and time could be infinitely divided, matter could not. His idea of a world made up of indivisible matter would in time become the prevalent theory of the universe. But at this point it was still very much a theory without a great deal of evidence.

His theory of forces acting on large objects like planets and apples had been so successful that Newton believed that if the ideas worked on the very large and the medium sized then why not on the very small. Why should there be a change in the way the laws of motion dictate the behaviour of the universe as we zoom in on my dice? The success of his calculus when applied to the movement of the planets depended on regarding them as single points with the mass concentrated at a point corresponding to the centre of gravity of the body. Maybe all matter consisted of particles like tiny planets whose behaviour was determined by his laws of motion. In his Principia he stated his belief that by applying his ideas to these individual particles one could predict the behaviour of all material things.

Newton’s theory of light also contributed to the growing feeling that an atomistic perspective was the best way to understand the world. Regarding light as a particle seemed the easiest way to describe the phenomena he documented in his book Opticks. The way that light reflected seemed to mimic the behaviour of a billiard ball as it bounced off the sides of the table. But from a scientific point of view there was no empirical evidence for this model of a universe made from indivisible particles.

Even with the microscopes that were emerging in the seventeenth century, you couldn’t see anything to justify this atomistic model. Even if you could see discrete objects, it wouldn’t prove anything about their indivisibility. But we can judge that the tide was turning by the fact that the atomistic view of matter made it into the popular culture of the time. Nicholas Brady’s ‘Ode to Saint Cecilia’, set to music by Purcell in 1691, talks of seeds of matter:

Soul of the World! Inspir’d by thee,

The jarring Seeds of Matter did agree,

Thou didst the scatter’d Atoms bind,

Which, by thy Laws of true proportion join’d,

Made up of various Parts one perfect Harmony.

The best evidence for an atomistic view of matter came a hundred years later from experiments that showed how matter combined to make new materials. And it was full of perfect harmony, as Brady had intimated.

ATOMIC ALGEBRA

It was the work of the English chemist John Dalton at the beginning of the nineteenth century that provided the first real experimental justification for thinking of matter as made of indivisible atoms. His discovery that compounds seemed to be made up of substances that were combined in fixed whole-number ratios was the breakthrough, and it led to the scientific consensus that these substances really did come in discrete packages.