Расчеты в Excel

Берем меньшее значение W из двух значений…

.jy1=h*b*b*b/12…

.jy2=hm*bm*bm*bm/12…

.jy3=hs*bs*bs*bs/12…

.jy=jy1+jy2+jy3… Момент инерции рельса по Y.

Выбор максимально удаленной части для оси Y-Y.

.wy=jy/(b/2)… Момент сопротивления изгибу рельса по YY.

.wy=jy/(bm/2)… Момент сопротивления изгибу рельса по YY.

Берем меньшее значение W из двух значений…

Выбираем меньшее значение момента инерции «j».

.rm=sqrt(jx/s)…

.rm=sqrt(jy/s)…

Запись программы в Excel.

Смотри открытый и закрытый листы Е 24.. ( Скачать из приложения ).

В колонке «Е»расчет промежуточных величин.

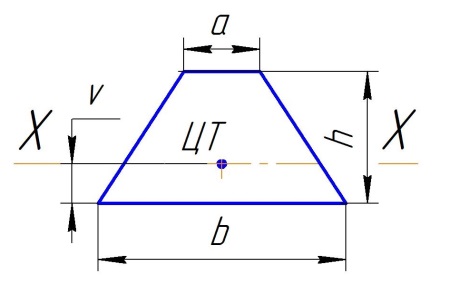
Параметры сечения трапеции

Высота трапеции = h.

Верх трапеции = a.

Основание трапеции = b.

Ось Х-Х проходит через Ц.Т. и параллельна основанию.

Ось Y-Y проходит через Ц.Т. и перпендикулярна основанию.

Рис. Сечение трапеции.

# Ведем расчет по классическим формулам 14-03-2020 г..

Pii = 3,141592654… Число Пи.

.x=(b-a)/2..

.y=(h*h)+(x*x)..

.ab=sqrt(y).. # Извлекаем квадратный корень ( Боковая грань трапеции ).

.xx=((a+x)*(a+x))+(h*h)..

.dt=sqrt(xx).. # Извлекаем квадратный корень (Диагональ трапеции ).

Ugrx=h/x..

Ugr=arctan(Ugrx).. # АрксТангенс от Ugrx в радианах.

Ug=Ugr*180/Pii.. # Угол в градусах…( Угол при основании ).

.s=h*(b+a)/2.. Площадь трапеции.

Далее расчет по оси Х-Х ( Ось Х-Х параллельна основанию ).

Разложим трапецию на два треугольника и на прямоугольник.

Sp=a*h.. # Площадь прямоугольника.

Jp=h*h*h*a/12.. # Момент инерции прямоугольника.

St=((b-a)/2)*h/2.. # Площадь одного треугольника.

.x=(b-a)/2.. # Основание одного треугольника.

Jt=h*h*h*x/36.. # Момент инерции одного треугольника.

.yt=h/3.. # Нейтральная ось от основания треугольника.

# Центр тяжести системы от основания ( нейтральная ось ).

.z=(((St+St)*yt)+(Sp*h/2))/(St+St+Sp).. ( На рисунке z обозначена как V ).

# Момент инерции двух треугольников со смещенным центром.

.at=z-yt.. # Смещение центра тяжести треугольников относительно Ц.Т. трапеции.

Момент инерции двух треугольников по Х-Х со смещенным центром.

Jts=2*(Jt+at*at*(St))..

# Момент инерции прямоугольника по Х-Х со смещенным центром.

.ap=z-(h/2).. # Смещение центра прямоугольника относительно Ц.Т. трапеции.

Jps=Jp+ap*ap*Sp.. Момент инерции прямоугольника по Х-Х со смещенным центром.

.jx=Jps+Jts.. # Момент инерции трапеции по оси ХХ.

.v=z.. # От основания – до нейтральной оси трапеции.

.wxv=jx/(h-v).. # Момент сопротивления изгибу для верхнего основания X-X.

.wxn=jx/v.. # Момент сопротивления изгибу для нижнего основания X-X.

.xr=jx/(Sp+St+St).. # jx / Площадь трапеции.

Rix=sqrt(xr).. # Извлекаем квадратный корень ( Радиус инерции ).

Далее расчет по оси YY.

# Разложим трапецию на два треугольника и на прямоугольник.

Sp=a*h.. # Площадь прямоугольника.

Jpy=a*a*a*h/12.. # Момент инерции прямоугольника.

# …

St=((b-a)/2)*h/2.. # Площадь одного треугольника.

.hy=(b-a)/2.. # Высота одного треугольника.

Jty=hy*hy*hy*h/36.. # Момент инерции одного треугольника Y-Y.

.yty=hy/3.. # Нейтральная ось от основания треугольника.

.ytyc=yty+(a/2).. # Нейтральная ось треугольника от оси Y-Y.

# Момент инерции двух треугольников со смещенным центром.

# .ytyc – Смещение центра треугольников от оси Y-Y.

Jtsy – Момент инерции двух треугольников по Y-Y со смещенным центром.

Jtsy=2*(Jty+ytyc*ytyc*(St))..

# Jpy – Момент инерции прямоугольника ( смещения нет ).

.jyy=Jpy+Jtsy.. # Момент инерции трапеции по оси Y-Y.

.wyv=jyy/(b/2).. # Момент сопротивления изгибу для Y-Y.

.xr=jyy/(Sp+St+St).. # ( jx / Площадь трапеции ).

Riy=sqrt(xr).. # Извлекаем квадратный корень ( Радиус инерции по Y-Y ).

Контрольный расчет:

Сечение в виде симметричной трапеции.

Высота трапеции = 30.

Основание трапеции = 50.

Верх трапеции = 20.

…

Боковая грань трапеции = 33.54102.

Диагональ трапеции = 46.097722.

Угол при основании = 63.434949 Градус.

Площадь трапеции = 1050.0.

Далее расчет по оси Х-Х.

Момент инерции по Х-Х одного треугольника Jt = 11250.0.

Центр тяжести системы Х-Х от основания = 12.8571.

Момент инерции двух треугольников по Х-Х со смещенным центром. = 26173.4694.

Момент инерции прямоугольника по Х-Х со смещенным центром. = 47755.102.

Момент инерции трапеции по оси ХХ. = 73928.5714.

Момент сопрот.изгибу по оси ХХ. = 4312.5 верх; 5750.0 низ;

Радиус инерции оси Х-Х = 8.391..

Далее расчет по оси YY.

Момент инерции по Y-Y одного треугольника Jt = 2812.5..

Момент инерции двух треугольников по Y-Y со смещенным центром. = 106875.0..

Момент инерции прямоугольника по оси Y-Y ( смещения нет ) = 20000.0..

Момент инерции трапеции по оси Y-Y. = 126875.0..

Момент сопрот.изгибу по оси Y-Y. = 5075.0..

Радиус инерции оси Y-Y = 10.9924..

Запись программы в Excel.

Смотри открытый и закрытый листы Е 25.. ( Скачать из приложения ).

В колонке «Е» расчет промежуточных величин.

Параметры сечения шестигранника

Рис. Шестигранник.

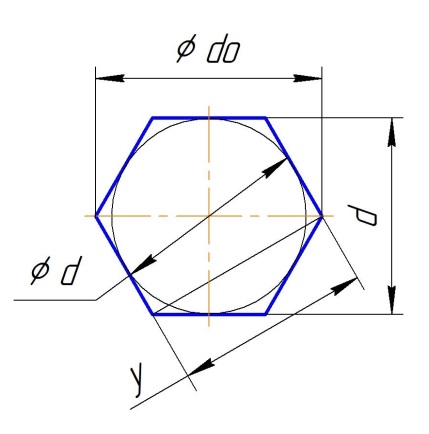
Ось Х-Х проходит через Ц.Т. Ось ХХ проходит через вершины на описанном диаметре do.

Ось Y-Y проходит через Ц.Т. и перпендикулярна оси Х-Х.

.d – Вписанный диаметр ( размер под ключ ).

.ss=0,866025403*d*d … Площадь шестигранника через вписанный диаметр.

.do=1,154700538*d … Описанный диаметр.

.ss=0,6495190528*do*do … Площадь шестигранника через описанный диаметр.

.ls=do/2 … Длина грани.

Для дальнейшего расчета представим шестигранник.

Как две трапеции соединенные основаниями.

Далее расчет заимствуем из расчета трапеции.

.h=d/2 … Высота трапеции.

.a=do/2… Верх трапеции ( Длина грани ).

.b=do… Основание трапеции.

Далее расчет трапеции:

.s=h*(b+a)/2.. Площадь трапеции.

Далее расчет по оси Х-Х ( Ось Х-Х параллельна основанию )..

Разложим трапецию на два треугольника и на прямоугольник.

Sp=a*h.. # Площадь прямоугольника.

Jp=h*h*h*a/12.. # Момент инерции прямоугольника.

St=((b-a)/2)*h/2.. # Площадь одного треугольника.

.x=(b-a)/2.. # Основание одного треугольника.

Jt=h*h*h*x/36.. # Момент инерции одного треугольника.

.yt=h/3.. # Нейтральная ось от основания треугольника.

# Центр тяжести системы ( трапеции ) от основания ( нейтральная ось )..

.z=(((St+St)*yt)+(Sp*h/2))/(St+St+Sp).. ( На рисунке z обозначена как V ).

# Момент инерции двух треугольников со смещенным центром.

.at=z-yt.. # Смещение центра тяжести треугольников относительно Ц.Т. трапеции.

Момент инерции двух треугольников по Х-Х со смещенным центром.

Jts=2*(Jt+at*at*(St))..

# Момент инерции прямоугольника по Х-Х со смещенным центром.

.ap=z-(h/2).. # Смещение центра прямоугольника относительно Ц.Т. трапеции.

Jps=Jp+ap*ap*Sp.. Момент инерции прямоугольника по Х-Х со смещенным центром.

.jx=Jps+Jts.. # Момент инерции трапеции по оси ХХ.

Ось ХХ трапеции смещена относительно оси ХХ шестигранника на величину V или z.

Jtz – Момент инерции трапеции по оси смещенной на величину V.

Jtz= jx + V*V*s..

Jse= Jtz+ Jtz.. Момент инерции шестигранника по оси ХХ.

Wse=Jse*2/d.. Момент сопротивления изгибу шестигранника по оси ХХ.

.rm=sqrt(Jse/(s+s))… Радиус инерции оси Х-Х.

Контрольные цифры:

Вписанный диаметр ( размер под ключ ) d = 86,60254038..

Описанный диаметр do = 100..

Площадь шестигранника = 6495,190528..

Запись программы в Excel.

Смотри открытый и закрытый листы Е 26.. ( Скачать из приложения ).

В колонке «Е»расчет промежуточных величин.

Расчет произвольного сечения

Расчет параметров произвольного сечения – эта программа весьма востребована при расчете на прочность разных, особенно сварных, конструкций. Программа часто применяется на практике.

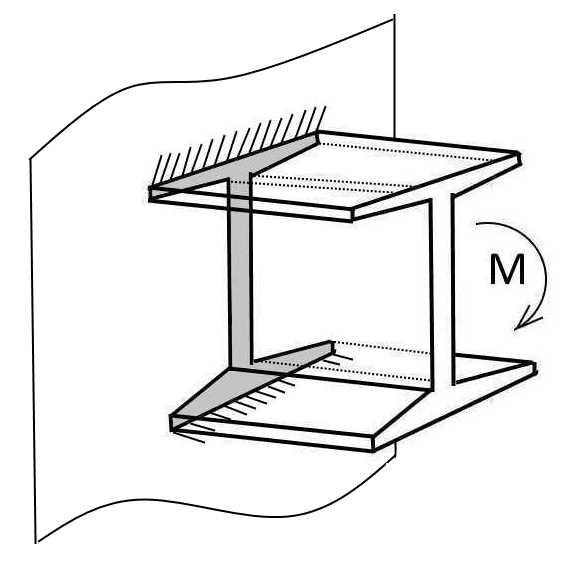
Рис. Приваренный двутавр.

….

….

Для примера: Двутавр № 10 .. Н=100 мм В= 55 мм. Wx= 39,7 куб.см.

Приварен к стальной стенке двумя швами L = 50 мм. Катет шва 10 мм.

Нагружен моментом М=100 кгс*метр.. М=10000 кгс*см..

Рекомендуется с каждего конца шва по 10 мм не учитывать в расчете, так как концы швов низкого качества.

Эфективное сечение шва = 0,7 от катета шва. И так имеем два шва с расчетными: длиной = 30мм.

С сечением 7 мм. Площадь сечения шва S = 210 кв.мм. Растояние по осям швов А=107 мм.

По программе Е_27 находим момент инерции швов; Jх = 1203860 мм в четвертой.

Программа определяет положение центра тяжести комплекса расчетных элементов.

Расчитаем величину растояния от центра тяжести до максимально удаленного от Ц.Т. элемента –

Обозначим максимальное растояние как «Y». Тогда Wx= Jх/Y..

Jх = 120,3860 см в четвертой. Wx=21120,35 куб.мм. Wx=21,12035 куб.см.

Напряжение в металле шва В=М/W.. В=10000/21,12035.. В= 473,48 кгс/кв.см.

Напряжение для шва вполне допустимое.

Напряжение изгиба в металле двутавра: В=М/W.. В=10000/39,7.. В= 251,9 кгс/кв.см.

Напряжение в металле двутавра низкое..

Если только два шва – то этого расчета достаточно. Если есть еще швы – то при добавлении элементов

Центр тяжести и Yмах будут изменяться. Программа расчитана на добавление девяти элементов, что

для практических расчетов вполне достаточно. Расчет можно закончить на любом по счету элементе.

На колонку «Е»можно не обращать внимания – там выводятся промежуточные результаты.

Расчет рекомендуется повторить не менее трех раз – часто бывают незаметные ошибки ввода данных.

Внимание – центр тяжести сместился при добавлении шва. Для нахождения момента сопротивления нужно найти максимальное растояние от центра тяжести системы до внешнего края системы «Y мах». W = J / Y мах…

,,,,

Заданное произвольное сечение представим как набор элементарных прямоугольников.

Вспомогательную ось Хv-Хv расположим по нижней грани самого нижнего прямоугольника.

Для первого этапа необходимо взять самый нижний прямоугольник фигуры.

Далее берем следующий по расположению по высоте нижнего края прямоугольник.

Определяем площадь, расстояние центра тяжести от оси Хv-Хv и

момент инерции первого прямоугольника. Формула [ 1 ].

Определяем площадь, расстояние центра тяжести от оси Хv-Хv и

момент инерции второго прямоугольника.

Находим расстояние центра тяжести системы двух прямоугольников от оси Хv-Хv.

Ось Х-Х проходит через центр тяжести системы из друх прямоугольников.

Находим момент инерции каждого прямоугольника относительно оси Х-Х

проходящей через общий центр тяжести. Формула [ 2 ].

Находим общий для системы момент инерции и общую площадь.

Определяем растояния от Ц.Т. крайних верхних и нижних точек системы.

Находим моменты сопротивления изгибу по верхней и по нижней граням системы.

Запишем результаты.

Рассчитанную систему принимаем как первый прямоугольник.

Добавляем еще один прямоугольник и повторяем выше приведенный расчет.

Расчеты ведем, пока не просчитаем все прямоугольники произвольного сечения.

Примечание: В программах типа «Бейсик, Питон, Паскаль» такие расчеты делаем закольцоваными

( циклическими ) – и количество добавляемых элементов не ограничено.

Excel имеет встроенную блокировку циклов. Поэтому программа ограничена десятью элементами.

Высота первого прямоугольника = h.

Ширина первого прямоугольника = b.

.j1=b*h*h*h/12… Момент инерции первого прямоугольника. Формула [ 1 ].

.w1=j1/(h/2)… Момент сопротивления первого прямоугольника.

.s1=h*b… Площадь сечения первого прямоугольника.

.xc1=h/2… Высота центра тяжести первого прямоугольника от оси Х-Х.

.m1=s1*(h/2)… Момент площади первого прямоугольника относительно оси Х-Х.

# Точка расчета № 1…

Высота второго прямоугольника = h1.

Ширина второго прямоугольника = b1.

Высота расположения основания

второго прямоугольника относительно оси Х-Х = hx.

.j2=b1*h1*h1*h1/12… Момент инерции второго прямоугольника.

.w2=j2/(h1/2)… Момент сопротивления второго прямоугольника.

.s2=h1*b1… Площадь сечения второго прямоугольника.

.xc2=(h1/2)+hx… Высота центра тяжести второго прямоугольника от оси Х-Х.

.m2=s2*((h1/2)+hx)… Момент площади второго прямоугольника относительно оси Х-Х.

.xx=(m1+m2)/(s1+s2)… Расстояние Ц.Т. от оси Хv-Хv системы двух прямоугольников.

R1=xx-xc1… Расстояние между Ц.Т. системы и Ц.Т. первого прямоугольника.

R2=xc2-xx… Расстояние между Ц.Т. системы и Ц.Т. второго прямоугольника.

Формула [ 2 ].

.j1x=j1+( R1*R1*s1)…Момент инерции первого прямоугольника относительно Ц.Т. системы.

.J2x=j1+( R2*R2*s2)…Момент инерции второго прямоугольника относительно Ц.Т. системы.

.Jx=j1x+j2x… Момент инерции системы двух прямоугольников относительно Ц.Т. системы.

Sx=s1+s2… Суммарная площадь двух прямоугольников.

.... .....

Далее в расчете принимаем систему двух прямоугольников за новый, первый прямоугольник у которого:

.s1=Sx… xc1=xx… j1=Jx… m1=Sx*xx…

Вводим данные следующего прямоугольника:

( считая его новым вторым прямоугольником ) и снова проходим весь расчет,

начиная с # Точки расчета № 1…

Для проверки можно пересчитать сечение «Рельс» и »Проверочный прямоугольник».

……..

Кстати все вышеизложенные расчеты эффективнее выполнять используя программы.

Программы можно скопировать из книги «Python 3 Полезные программы книга третья.».

Программы значительно экономят время и уменьшают вероятность ошибок в расчетах..

Программы можно выполнить так же в Excel.

Запись программы в Excel.

Смотри открытый и закрытый листы Е 27.. Е 28.. ( Скачать из приложения ).

В колонке «Е»расчет промежуточных величин.

Колонку»D»и»Е»Делаем с запасом по высоте – Выдеяем с «D2» до «D28» со свойствами «Цифровой»

точность шесть знаков после запятой, центровка по левому краю, шрифт «16», «Скрыть формулы».

Колонка «Е»– точно так же.

В лист Е 28 результат предыдущего расчета переносим – записав его на бумажке и вводя затем вручную.

При переносе результата можно ошибиться. Более сложное действие описано ниже..

@014. – Вставим лист № 2.

Смотри открытый лист Е 27хх.. ( Скачать из приложения ).

Заполнив открытый лист Е 27хх .. также как в предыдущем случае лист Е 27..

Области результатов нужно выделять с большим запасом вниз и задавать по шесть знаков после запятой.

Затем можно просто скопировав лист Е 27 под именем Е 27хх, дополним его листом № 2.

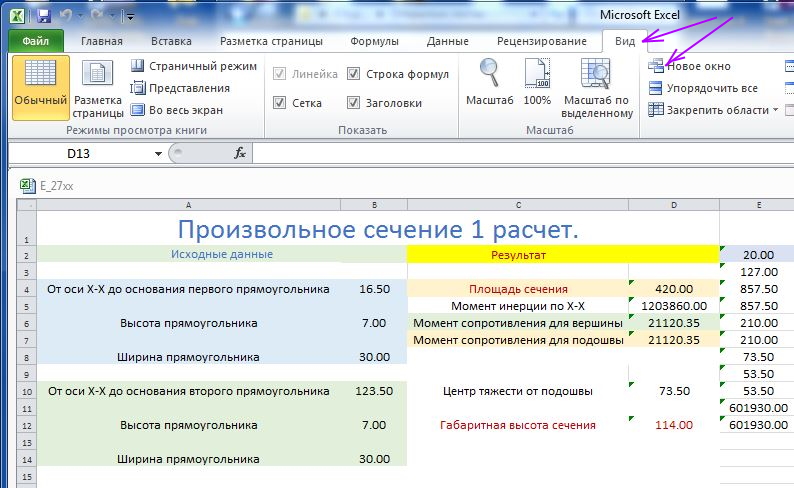
Для этого в верхней строке режимов ( Лента от «Файл» до «Вид») перейдем в режим «Вид»-

щелкнем на иконке «Новое окно»-

Рис. Экран Excel Произвольное 1.

…

…

Щелкнем на иконке «Добавить лист».

Рис. Экран Excel Добавить лист.

…

…

Появится лист №2 – второй лист заполняем так же как заполняли лист Е 28…

При заполнении второго листа – результаты из первого листа ( цифры ) переносим вручную.

@015. – Перенос результатов копированием.

# Точка расчета № 2…

Области результатов нужно выделять с большим запасом вниз и задавать по шесть знаков после запятой.

Выделяем область результатов левой кнопкой мыши – на листе № 2..

На выделенной области щелкаем правой кнопкой «Скопировать».

Выделяем и копируем весь столбик результатов.

Рис. Экран Excel Перенесли результаты.

…

…

На листе № 2 в колонке D1 выделяем ячейку D15 левой кнопкой мыши –щелкаем правой кнопкой

«Вставить». в режиме «123». В этом режиме произойдет вставка цифр результатов. Формулы стоящие за цифрами в этом режиме не копируются.

Рис. Экран Excel Скопированные цифры.

…

…

Далее На листе № 2 – выделяем ячейку В4 – удаляем цифру площади в исходных данных в ячейке В4. Выделяем ячейку D15 – левой кнопкой – щелкаем «Вставить». Блок результатов скопирован в ячейки

D15.. D21 .. Левой кнопкой выделяем ячейку D15.. Щелкая правой кнопкой – копируем величину площади

из ячейки D15.. ( из одной ячейки ) – Выделяем левой кнопкой ячейку В4 –

правой кнопкой вставляем в ячейку В4. В режиме «123». данные из ячейки D15..

Рис. Экран Excel Режим вставки.

,,,

,,,

Аналогично удаляем значения в ячейках В6 и В8 и заменяем цифрами из ячеек D21 и D16. Переносим по очереди по одной ячейке.

В ячейки В10, В12, В14 – вводим значение нового прямоугольника. В колонке D4.. D10 появились данные сечения с вновь добавленным прямоугольником. Если все элементарные прямоугольники закончились –

То расчет закончен. Если надо добавить еще прямоугольник, то выделяем область D15.. D21 – и удаляем

Все данные – затем переходим в # Точка расчета № 2…

Процедура довольно капризная – нужно строго соблюдать последовательность действий.

Внимание: Открыв для работы расчетный лист – можно менять цифры только в колонке для ввода исходных данных. Удаляя или меняя цифры в других колонках Вы на самом деле разрушаете скрытые за ними формулы.

В результате лист будет испорчен, работать не станет.

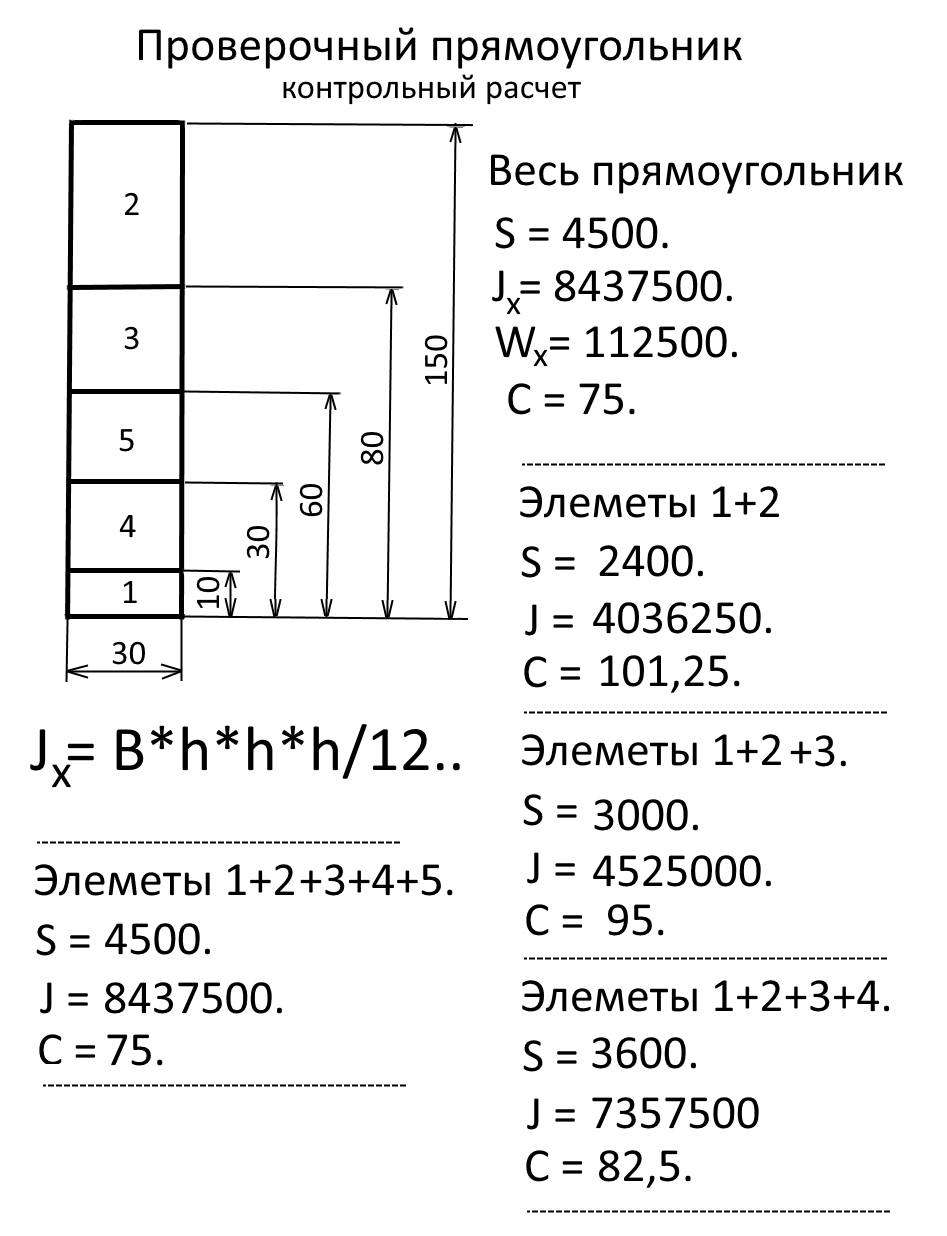
Рис. Проверочный прямоугольник.

…..

,,,,,

Проверка программы – и своих действий при работе с программой:

Проверочный прямоугольник разбили на пять прямоугольников.

Нулевая ось – по нижнему краю самого нижнего прямоугольника. Xv – Xv

Размер «С» это размер высоты центра тяжести системы от Нулевой оси Xv-Xv.

На листе Е 27хх № 1.. Ввод данных начинаем с прямоугольника № 1. – Самого нижнего.

Затем вводим данные прямоугольника № 2. – Самого верхнего.

Запишем результаты и введем их Е 27хх № 2.. Далее работаем с листом Е 27хх № 2..

Последовательно добавляя прямоугольники и контролируя результаты.

В итоге данные системы из пяти прямоугольников должны полностью соответствовать данным

Одного целого прямоугольника высотой = 150, шириной = 30..

Центр тяжести системы при расчете всегда выше оси Xv-Xv.

,,,,

@016. – Программирование ( запись ) Макроса .

Более сложный при разработке, но значительно удобней при работе режим с применением Макросов

при копировании результатов первого и промежуточных расчетов.

В виду важности данной программы – описываем разработку листа полностью и пошагово.

.01- Открываем файл Е_27хх сохраняем его как Е_27хх_М.

На Листе №1 Колонка «В3-В24» Запись исходных данных. Проверяем – Выделить – Формат ячеек –