
Население Земли как растущая иерархическая сеть II
Сравним теорию с этой гиперболой. Для этого сдвинем начало отсчета времени от начала новой эры к неолиту, а численность будем измерять в клаттерах. За точку отсчета на оси времени возьмем 8154 год до н. э. (255·39,75 = 10136, 10136 – 1982 = 8154, 10136 + 39,75 ≈ 10180).
И для удобства расчетов ищем зависимость от (-t), т. е. отсчитываем время от 8154 года до н. э. в прошлое. Тогда t = 0 – начало неолита, а t = -10180 – точка сингулярности гиперболы демографического роста. С учетом зомби-коэффициента k = 1.1 находим число клаттеров Сети как функцию времени:

Рис. 2. Зависимость числа клаттеров Сети человека в млрд от (– t) по формуле Мак-Эведи и Джоунса. Время отсчитывается в годах от начала неолита в прошлое.
Алгоритм дает:

Рис. 3. Зависимость числа клаттеров Сети человека от времени в циклах согласно теории.
Построим в одних координатных осях графики теоретической и эмпирической зависимости числа клаттеров Сети от времени. Время отсчитываем в прошлое в циклах и в логарифмическом масштабе: от 8 тыс. года до н. э. до 1,7 млн лет до н. э. По оси ординат, для лучшего сравнения, логарифмический масштаб применять не будем.

Рис. 4. Сравнение алгоритма теоретической зависимости и гиперболы Мак-Эведи и Джоунса для времен от начала эволюции до неолита.
Алгоритм дает целое число клаттеров, т. е. его погрешность составляет 65536 носителей. Наибольшее отклонение теории от гиперболы (4) равно 11 %. Теоретическая кривая почти не отличается от гиперболы Мак-Эведи и Джоунса, следовательно, теория полностью соответствует имеющимся демографическим данным для времен до 8154 года до н. э. Точность всех дат зависит от точности определения начала перехода: 1982 год (слабо) и от точности, с которой известна постоянная цикла τ = 39.75 лет (сильно).
Второй этап роста Сети человека
Последние 255 циклов роста Сети человека1.7 млн лет и 42142 цикла понадобилось Сети, чтобы собрать 256 клаттеров. 42143-ий цикл был первым циклом, в процессе которого с нуля был собран дочерний клаттер. Начало этого цикла – восемь тысяч лет до нашей эры – было началом эпохи неолита: времени перехода от охоты и собирательства к оседлому образу жизни, появлению сельского хозяйства, домашних животных, культурных растений.
Именно в этот момент времени Сеть человека достигает гармонической стадии своего роста, но вопрос о том, как это повлияло на социум, мы рассмотрим позже. Почему десять тысяч лет тому назад началась новая эра в истории человечества?
На самом деле Сети это было известно еще во время старта, и по мере приближения к этому моменту она выбрала из всех возможных сценариев тот, который обеспечивал необходимую динамику ее роста.
Здесь нужно ясно понимать, что не культурные и технологические достижения неолита были первопричиной ускоренного роста численности населения мира, а плановые потребности Сети по приросту числа ее клаттеров.
Здесь и в дальнейшем Сетью (в смысле имени собственного) будем называть изначально существующую и прогрессирующую ментальность природы, выражающуюся в плановом, эквифинальном росте биниальной иерархической сети соответствующего ранга на множестве носителей текущей авангардной системы эволюции.
В качестве носителей иерархических сетей различных рангов выступали представители авангардных систем ядерной, химической, биологической и социальной эволюции – от бариона до человека. Рост Сети человека от 256-ти до 65536-ти клаттеров описывается теоретической гиперболой:
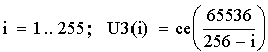
Рис. 1. Теоретическая зависимость числа клаттеров Сети от номера цикла от неолита до перехода; ce(X) – ближайшее целое, меньшее или равное X (ce(2.3) = 2).
Найдем зависимость численности носителей Сети от 8154 года до н. э. до 1982 года н. э. Интерполируем кубическими сплайнами функцию численности населения мира, заданную на сетке с шагом 39.75 года:
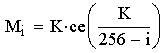
Рис. 2. Зависимость численности носителей Сети от 8154 года до н. э. до 1982 года.
Казалось бы, что время роста сети с точностью до года – это абсурд. Но смысл предлагаемой здесь гипотезы в том, что все стадии и этапы эволюции человека (и не только человека) определяются ростом иерархической сети. Мы считаем, что время начала каждого цикла должно выражаться с «абсолютной» точностью.
Запишем это в системе MathCAD:
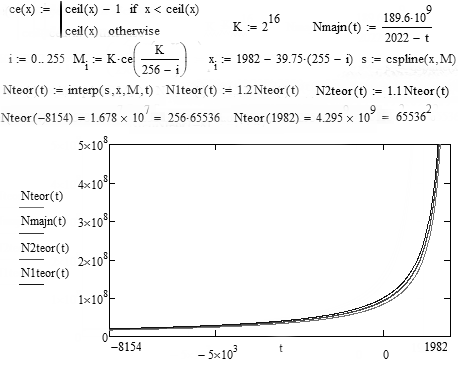
Рис. 3. Сравнение гиперболы Мак-Эведи и Джоунса с теоретической гиперболой при k = 1.0, k = 1.1, k = 1.2 (k – эомби-коэффициент) на временах от начала неолита до 1982 года.
При k =1.1 теоретическая гипербола сливается с гиперболой Мак-Эведи и Джоунса. Сравним теперь теоретическую гиперболу (k = 1.1) с гиперболами Фёрстера и Хорнера за последние два столетия:
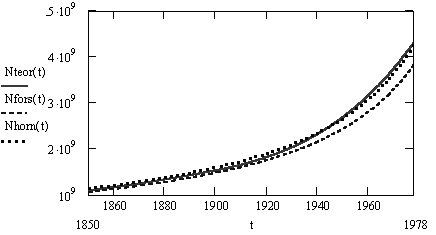
Рис. 4. Зависимость численности Земли за последние два столетия для гипербол Фёрстера, Хорнера и теоретической гиперболы.
Теоретическая гипербола практически сливается с гиперболой Хорнера. Итог таков: предложенная модель на интервале от -8154 до 1982 года согласуется с демографическими данными так же хорошо, как и все эмпирические гиперболы роста населения Земли. Главный же вывод состоит в том, что предложенная модель описывает рост населения Земли в точном соответствии с демографическими данными на всем протяжении истории развития человечества.
При этом сама гиперболическая зависимость, константы Капицы К и τ, а также постоянная Фёрстера С выводятся из идеальной математической схемы и космологических данных (Tu = 13.81 млрд лет) без всякой связи с работами Фёрстера и Капицы.
Теперь о точности теоретической зависимости. Прежде всего, важно еще раз отметить то, что теоретическая гипербола – это точечная функция и областью ее определения и множеством значений являются 256 фиксированных значений.
Согласно первому закону Сети точные значения числа носителей могут быть получены только в точках сетки, образованной обратным отсчетом времени от 1982 года в прошлое с шагом τ = 39.75 года. (Речь здесь идет о приоритете роста по циклам, который может и нарушаться для предотвращения сбоя по гармоническим и тем более совершенным стадиям роста Сети, обладающим бо́льшим приоритетом.)
Внутри же циклов значения теоретической функции могут быть лишь интерполированы. Причем результаты этой интерполяции как теоретические данные могут быть неточны и даже ошибочны. Эта математика хорошо соответствует закону роста, который не обязывает население мира расти в точности по закону гиперболы, а лишь расставляет систему приоритетов: значений численности носителей в начале и в конце каждого цикла, а также в предзаданные моменты гармонического достижения.
Кроме того, необходимо помнить, что зомби-коэффициент k, учитывающий народонаселение, неспособное выступать в качестве носителей Сети, который мы ввели как величину неизменную и равную 1.1, на самом деле менялся (видимо уменьшался) на протяжении всей истории развития человечества. Поэтому не следует забывать про все эти оговорки при оценке погрешности, с которой может быть определена численность населения Земли, скажем, в 1370 году.
Последний цикл роста СетиОн особенный, ведь за время его прохождения прирост носителей был таким же, как за все предыдущие 42396 циклов. Это был последний переход Сети человека от самой большой гармонической сети к сети совершенной. Начался он в 1942 году и закончился в 1982-м.
Самый бурный и неповторимый этап развития прошла и Мир-система. Атомная энергия, генетика, космос, телевидение, компьютеры… И это несмотря на вторую мировую войну и риск развязывания третьей.
Первая половина цикла – замедление роста, перегиб, спад; вторая половина – быстрый взлет с последующей стагнацией скорости роста. Динамику роста численности внутри этого цикла предложенная гипотеза не объясняет (и не должна).
Видимо, форсаж Сети связан с ее стремлением как можно более плавно вписаться в демографический переход. Но первый закон остается в силе: об этом говорят демографические данные. Действительно, численность носителей Сети (k = 1.1) в 1942 году составила примерно 2.15 миллиарда (2.35/1.1), а в 1982-м – удвоилась и составила примерно 4.30 миллиарда (4.6/1.1).
И вот что потрясает, как и в момент начала неолита, ведь все научные, технологические, культурные и прочие достижения, приведшие к удвоению населения за столь короткий промежуток времени, были заранее спланированы Сетью. Иначе как бы она смогла выполнить первый закон своего роста (постоянство времени цикла)?
Но процесс развития зависит от всей своей предыстории, и, скажем, без знания электродинамики создать компьютер невозможно, значит, уравнения Максвелла должны были быть открыты где-то за век до того. Так каким же непостижимым по мощи должно быть то сознание, которое способно на такое историческое моделирование и столь безукоризненную реализацию своих расчетов!
В 1982 году произошло событие, оставшееся незамеченным. Сеть достигла совершенства, а вид Homo sapiens – потолка в своем развитии. Закончилась эволюция нашего вида – вот почему столь значим этот последний цикл в его развитии.
Демографический переход
Так что же такое глобальный демографический переход? Внимательный читатель, наверное, давно уже понял, что это такое. О, да! – это Сеть снимает с себя копию и заходит на следующий виток спирали – вперед к новому виду! Попробуем разобраться, как она это делает. Прежде всего, уточним, что такое демографический переход. В демографии под ним понимается заключительный этап роста населения, который начинается в момент наивысшего набора скорости роста численности и заканчивается в момент наибольшего спада ее прироста.
Здесь же – и это логично – считать, что это временной интервал, в течение которого совершается операция репликации, отсчитываемый от того момента времени, когда Сеть становится совершенной до того момента, когда создается ее копия, прокладываются связи и запускается рост Сети следующего, пятого ранга.
Сеть измеряет время циклами – квантами исторического времени. Время цикла Сети было предопределено прогрессией эволюции и общим числом циклов, включающим циклы перехода. Но сколько всего циклов Сеть человека отложила на переход? Ясно, что больше одного, т. к. к 2022 году численность человечества будет меньше 9 млрд. Следовательно, переход будет состоять из двух или большего числа циклов. Поскольку время роста сети «квантовано» и измеряется целым числом циклов, логично предположить, что переход займет ровно два цикла характерного времени Капицы.
Действительно, за последний цикл роста Сети 1942-1982 гг. ее размер удвоился и, соответственно, вдвое возросла численность населения Земли. Среднее значение скорости роста численности составило 1,1·2,15/40 = 60 млн/год. В середине шестидесятых годов прошлого века она достигла в своем относительном выражении абсолютного за всю историю человечества максимума два процента в год и началось ее снижение.
Поскольку в процессе перехода Сети потребуется скопировать вдвое большее число носителей, чем на последнем цикле, причем скорость ее роста будет непрерывно (вплоть до нуля) уменьшаться, то минимальное время, которое ей на это потребуется, равно удвоенному характерному времени Капицы. Следовательно, откладываем на глобальный демографический переход ровно два цикла характерного времени (столько же, сколько в модели Капицы).
Его продолжительность составит 2τ = 80 лет, и завершится он в 2062 году (1982 + 80 = 2062). Численность населения мира к этому времени достигнет значения 9.2 ± 0.2 млрд человек (8.6·1.07) и более меняться не будет (зомби-коэффициент на время перехода считаем равным 1.07). Динамику роста внутри перехода наша модель в точности предсказать не может. (Заметим, что исследование этой динамики как по отдельным странам, так и по миру в целом позволит лучше понять как функционирует Сеть.)
Первый цикл переходаЕго начало – 1982 год, конец – 2022-й. В 2000 году население мира достигло значения 6.1 млрд, а темпы прироста – своего максимума: 87 млн человек в год. Вторая производная от численности по времени обратилась в нуль. При такой скорости роста население Земли к 2021.5 году составило бы N = 6.1 + 0.087·21.5 = 7.97 млрд человек, что меньше, чем 9.2 млрд (фактически на начало 2021 года N = 7.84 млрд). По-видимому, скорость роста населения будет продолжать уменьшаться в течение всего второго цикла.
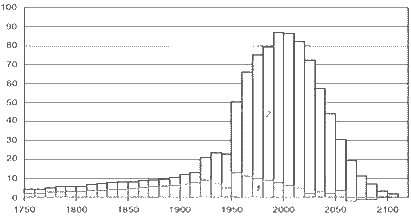
Рис. 1. Демографический переход. Годовой прирост населения мира в млн человек 1750–2100 гг., усредненный за декады. 1 – развивающиеся страны, 2 – развитые страны.
Второй цикл переходаЕго начало – 2022 год, конец – 2062-й. Этот цикл является завершающим для сети 65536 и обещает быть самым необычным. В его конце скорость роста численности вместе с высшими производными должна будет устремиться к нулю. И выполнить это условие не так-то просто.
Математика не знает такой элементарной, непрерывной со всеми производными функции, значения которой на конечном интервале возрастают до некоторой величины и далее не меняются. Такую функцию нельзя также представить как конечную комбинацию элементарных. С точки зрения математики ее можно, например, представить как бесконечный ряд (интеграл) такой, как ряд (интеграл) Фурье.
В конце второго цикла перехода произойдет стабилизация численности на уровне 9.2 ± 0.2 млрд человек. Однако непонятно как все это будет реализовано на множестве подмножеств сообществ, объединенных по разным признакам своего родства.
Можно было бы предположить, что Сеть прибегнет к уже испытанному приему временно́й дисперсии Мир-Cистемы, как это было с рядом развитых стран, уже прошедших свой демографический переход. Но слишком мало остается времени, «хвосты» у этих функций длинные, а логистическая кривая Сети не нужна.
Ведь в 2062 году должен быть собран второй клаттер Сети 4 294 967 296. Сеть всегда выполняет план в приоритетных точках своего роста. В соответствии со вторым законом, феномен сознания связан с Сетью. Те, кто находятся вне Сети представляют собой «неуправляемую» часть социума. Их доля составляет примерно 9 %, т. е. она невелика; от ее величины очевидным образом зависит способность социума к прогрессивному развитию – это как минимум, и управляемость обществом вообще – как максимум.
Если Сеть выберет сценарий «длинных хвостов», то в конце второго цикла перехода следует ожидать резкого роста людей с больной психикой. Такие явления, как сумасшествие или впадение в кому, можно рассматривать как факт замены Сетью «игрока», а ремиссия и, соответственно, выход из комы – как его возврат.
Возможен еще один сценарий, имеющий меньшие издержки. Если в социуме будут возбуждены колебания прироста численности на множестве подмножеств различных социальных групп – погрешность Сети может быть значительно уменьшена. Чисто схематически все это можно представить так:
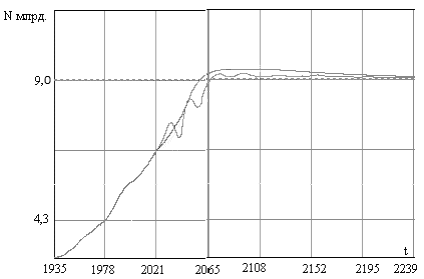
Рис. 2. Варианты роста населения мира в процессе демографического перехода согласно теории (схема).
Итог такой: последний цикл Сети, особенно его концовка с продолжением, – время стрессов, эпидемий, роста числа психических и прочих заболеваний, возможно, локальных войн и природных катаклизмов. Численность населения Земли достигнет значения 9.2 ± 0.2 млрд человек и многие тысячи лет меняться практически не будет. (В июле 2020 года (пандемия covid-19) ученые из Вашингтонского университета опубликовали в медицинском журнале The Lancet прогноз на численность населения мира к концу текущего столетия: 8.79 млрд человек, что на два с лишним миллиарда меньше, чем прогноз ООН 2019 года: 11 млрд.)
Уравнение Капицы
Пусть имеется сеть, размер которой равен М, т. е. ИС, содержащая М клаттеров. И допустим, что за цикл новый клаттер собрать не удается. Т. е. рассмотрим сначала первый этап роста. На копирование одного клаттера требуется М носителей и всего за цикл их будет скопировано М2. Если N – полная численность носителей Сети, то:
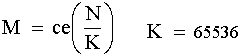
Рис. 1. Число носителей, идущих на копирование одного клаттера.
Здесь ce(X) – ближайшее целое, меньшее или равное числу X. Прирост численности носителей за цикл равен:
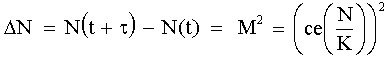
Рис. 2. Прирост носителей за цикл.
К этому разностному уравнению необходимо добавить условие завершение цикла. Как только в процессе итераций число носителей N(t) достигнет значения, достаточного для сборки нового клаттера, нужно сделать подстановку:

Рис. 3. Условие подстановки.
Вот решение этого уравнения в системе MathCAD (здесь τ = 1, время измеряется в циклах):

Рис. 4. Алгоритм решения разностного уравнения.
Зависимость численности носителей от времени получается такой же, как в модели роста клаттеров по циклам U2(C). Если число собранных за цикл клаттеров значительно меньше размера сети (второй этап ее роста), то и в этом случае данное разностное уравнение служит хорошим приближением алгоритму.
При этом N(t) мало меняется за время τ. Если, к тому же N(t) >> K, то дифференциальное уравнение может служить хорошим приближением разностному.

Рис. 5. Переход от разностного уравнения к уравнению Капицы.
Здесь τ – время цикла сети, равное постоянной времени Капицы. Этим же уравнением описывается теоретическая гипербола и численность населения мира N2(t) = kN(t). Важно понимать следующее: зависимость N(t), задаваемая алгоритмом роста сети, может быть описана уравнением Капицы на всем протяжении гиперболического роста.
Тем не менее гиперболы роста на этапах до момента начала неолита и после момента начала неолита – отличаются. Дело в том, что теоретически рост сети на первом этапе описывается уравнением Капицы лишь приблизительно.
Тогда как на втором этапе, когда рост согласно алгоритму резко ускоряется, он может быть в точности описан теоретической гиперболой, которая, как мы неоднократно отмечали ранее, является «точечной» функцией (т. е. ее областью определения и множеством значений являются 256 фиксированных значений времени и численности), все точки которой лежат на гиперболе, являющейся решением уравнения Капицы.
Поэтому аппроксимирующие зависимости численности от времени до, и после начала неолита – отличаются, и общее решение «сшивается» из двух различных гипербол. Поэтому в момент начала неолита скорость роста как функция времени (теоретически) претерпевает разрыв.
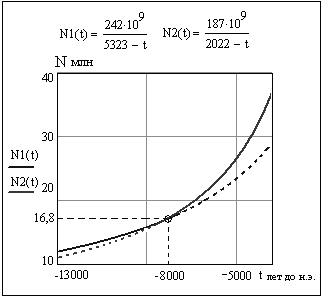
Рис. 6. Неолитический скачок скорости роста населения Земли.
Теоретическая гипербола как результат алгоритма роста сети совпадает с гиперболой, являющейся решением уравнения Капицы. Для описания гиперболического роста численности населения мира необходимо домножить N(t) на зомби-коэффициент k ≈ 1.1: N2(t) = kN(t). Парадоксальная гиперболическая зависимость численности населения Земли от времени возникает (при заданном алгоритме роста сети) по причине постоянства времени цикла.
История
Гармонические сети и ноосфера
Можно ли всерьез сомневаться в том, что разум – эволюционное достояние только человека? И, следовательно, можем ли мы из какой-то ложной скромности колебаться и не признавать, что обладание разумом дает человеку коренной перевес над всей предшествующей ему жизнью?
Пьер Тейяр де ШарденОсобые дарования, которые мы обсуждаем, ясно указывают на существование в человеке качеств, которые он не мог унаследовать от своих животных предков, – чего-то, что мы с большим основанием отнесли бы к духовной сущности… помимо материальных объяснений, законов и движущих сил.
Aльфред Рассел УоллесСуществует принципиальный разрыв между человеком и всеми другими животными. Мышление человека первично коллективно и изначально осуществлялось сетью мозгов, связанных речевыми сигналами. Лишь по мере развития общества формируется индивидуальное мышление.
Б.Ф. ПоршневПрежде всего, хотелось бы отметить, что эта глава, в отличие от предыдущих, носит лишь эвристический характер. Это первое приближение, первая попытка дать объяснение сокращающимся по закону прогрессии историческим циклам на основе предлагаемой здесь гипотезы. Возможно, все это покажется вымыслом или даже бредом, но должна же существовать какая-то причина ускорению исторического времени и глобальным историческим циклам…
* * *Попробуем сначала представить как росла Сеть. Процесс ее роста, который будет здесь описан, – всего лишь вольная интерпретация математического алгоритма, который методом проб и ошибок был выбран нами таким, чтобы размер сети как функция номера цикла рос по закону простой, «школьной» гиперболы. Что при постоянстве времени цикла приводит к гиперболическому росту населения мира.
В этой вольной интерпретации клаттер-носитель (в приложении нашей модели к процессу роста численности населения Земли) – это клаттер, связанный с каждым человеком; но это не человек в биологическом и психическом смысле этого слова, а некая глубинная и бессмертная сущность, которая живет в каждом человеке и которая связана с его подсознанием. Эта сущность: энтелехия, душа, монада – связана с Сетью, точнее, является ее частью и может влиять на поступки людей, способствуя выполнению ее плана.
Процесс копирования узлов и связей сети в математической модели можно интерпретировать как репликацию некоторых клаттеров-носителей в каждом сетеобразующем клаттере Сети человека. Для зазеркального мира сетей здесь постулируется фундаментальное свойство жизни: способность к размножению, т. е. способность каждой частице живого создавать собственную копию.
В тот момент, когда был собран первый клаттер Сети человека, 1.7 млн лет тому назад, из 65536 клаттеров-носителей была выбрана пара самых «продвинутых». Когда в процессе операции репликации был собран второй клаттер и стартовал рост этой сети, в каждом из двух ее клаттеров было по два «продвинутых» клаттера-носителя, способных поддерживать связи более высокого уровня растущей сети четвертого ранга.
Именно этим «продвинутым» клаттерам Сеть человека и позволила размножаться. Клатер-носитель – единственный клаттер Сети человека, который не может существовать без связи с материальным миром (с миром барионной материи?), т. е. он не может существовать без своей пары – носителя-человека или просто человека.
Годовой прирост клаттеров-носителей, контролируемый Сетью, умноженный на зомби-коэффициент k, должен быть равен человеческому годовому естественному приросту. Клаттер-носитель после гибели связанного с ним человека «пересаживается» на какого-то другого. Причем это необязательно должен быть кто-нибудь из детей двух, трехлетнего возраста, в очередном порядке обретающих своего клаттера-носителя (ангела-хранителя?), а, например, это может быть человек, пришедший в сознание после клинической смерти, временно удаленный из Сети.
Здесь еще нужно учесть то, что в данном случае из всего множества клаттеров-носителей выделяется некоторое динамическое подмножество лидеров: множество «продвинутых» клаттеров, что представляет собой, по сути, сетевой искусственный отбор. При этом клаттеры-носители наделяются индивидуальностью и постоянной «пропиской» в пределах каждого сетеобразующего клаттера.
Нарушенную таким образом однородность состава клаттеров математической модели можно восстановить, постулируя межклаттерное перемешивание клаттеров-носителей при замещении носителя открепленным (не скопированным) клаттером-носителем.
Но Сеть не только постоянно «затыкает бреши», но еще и растет, что, собственно, и описывает математическая модель ее роста. Человеческий естественный прирост (полученный за 2-3 года до…) «подхватывается» только что рожденными клаттерами-носителями во время сборки очередного клаттера Сети человека.