
Как работает мозг
Смею надеяться, что вознаграждением за долгие рассуждения о ментальных вычислениях и ментальных репрезентациях, через которые я вас провел, стало понимание того, на какую сложность, тонкость и гибкость способен человеческий разум, даже если он – всего лишь машина, всего-навсего бортовой компьютер робота, сделанного из живых тканей. Нам не нужны духи или оккультные силы, чтобы объяснить интеллект. Не нужно нам и игнорировать очевидное в надежде сделать свое объяснение более научным, утверждая, что человек – всего лишь куча обусловленных ассоциаций, марионетка генов или раб примитивных инстинктов. Мы можем совместить живость и проницательность человеческого ума с механистической основой, без которой сложно его объяснить. Последующие главы, в которых предпринимается попытка дать объяснение здравому смыслу, эмоциям, общественным отношениям, юмору, искусству, основаны на фундаменте представлений о сложной вычислительной психике.
Действующий чемпион
Конечно, если бы никто не взялся оспаривать истинность вычислительной теории, это означало бы, что она бессодержательна. На самом деле она подвергалась самой жесткой критике. Как в случае с любой теорией, которая стала столь незаменимой, обыкновенных придирок было недостаточно; чтобы разрушить ее, нужно было подорвать ее основания, никак не меньше. За эту задачу решили взяться два ярких автора. Оба выбрали оружие вполне подходящее для такого случая, но совершенно разное: один решил прибегнуть к здравому смыслу; второй – к понятным лишь посвященным физике и математике.
Первым с критикой выступил философ Джон Серль. Серль считает, что опроверг вычислительную теорию сознания еще в 1980 году с помощью мысленного эксперимента, который он с небольшими изменениями позаимствовал у другого философа, Неда Блока (который, как ни парадоксально, был одним из наиболее активных сторонников вычислительной теории). Версия Серля стала известна под названием «китайская комната». Человека, который не знает китайского языка, помещают в комнату. Под дверь подсовывают листки бумаги с какими-то закорючками. Человеку дают целый список сложных указаний вроде следующего: «Если увидите надпись [закорючка закорючка закорючка], напишите [каракули каракули каракули]». Некоторые из этих правил предписывают подсовывать написанные им каракули обратно под дверь. Он достаточно прилежно выполняет инструкции, не подозревая, что закорючки и каракули – это китайские иероглифы, а инструкции – это программа искусственного интеллекта, предназначенная для того, чтобы отвечать на вопросы о рассказах на китайском языке. Человек, находящийся по другую сторону двери, делает вывод, что в комнате находится человек, владеющий китайским как родным. Так вот, если понимание заключается в том, чтобы запустить подходящую компьютерную программу, значит, участник эксперимента понимает китайский, потому что он как раз использует подходящую программу. Но этот человек не понимает ни слова по-китайски; он просто манипулирует символами. Следовательно, понимание – и, если уж на то пошло, любой другой аспект интеллекта – не то же самое, что манипуляция символами или вычисление90.
Серль утверждает, что программе не хватает интенциональности: связи между символом и тем, что он обозначает. Многие интерпретировали его слова так, будто программе не хватает сознания. Действительно, Серль считает, что сознание и интенциональность тесно связаны, ведь мы осознаем, что мы имеем в виду, когда думаем о чем-то или используем какое-либо слово. Интенциональность, сознание, другие явления мыслительной деятельности обусловлены не обработкой информации, заключает Серль, а «реальными физико-химическими свойствами реального человеческого мозга» (хотя что это за свойства, он так и не уточняет)91.
«Китайский эксперимент» вызвал поистине невообразимые дебаты. В ответ на него было опубликовано более сотни статей, и для меня это стало прекрасной причиной удалить свое имя из всех списков участников интернет-обсуждений. Тем, кто утверждает, что вся комната в целом (человек плюс список инструкций) понимает китайский язык, Серль отвечает: ладно, представим, что этот парень выучил наизусть все правила, теперь он производит все вычисления в уме и работает вне комнаты. Комнаты больше нет, но наш с вами манипулятор символами по-прежнему не понимает по-китайски. Тем, кто заявляет, что у этого человека нет никакой сенсорно-двигательной связи с миром, и что именно это – главное недостающее звено, Серль отвечает: предположим, что поступающие в комнату каракули – выходной сигнал телевизионной камеры, а закорючки, поступающие из комнаты, – команды роботизированной руке. Теперь у него есть связь с миром, но он по-прежнему не говорит на китайском языке. Тем, кто говорит, что эта программа не отражает деятельность мозга, Серль приводит аналог «китайской комнаты», придуманный Блоком, – «китайский спортзал»: миллионы людей в огромном спортзале ведут себя так, словно они – нейроны; они кричат друг другу по рации сообщения, воспроизводя работу нейронной сети, которая отвечает на вопросы к рассказам на китайском языке. Но и люди в этом спортзале понимают по-китайски не больше, чем тот парень в закрытой комнате.
Тактика Серля заключается в том, чтобы вновь и вновь обращаться к нашему здравому смыслу. Так и кажется, что он говорит: «Эй, да ладно! Вы что, хотите сказать, что этот парень понимает по-китайски??!!! Да хватит вам! Он не понимает ни слова! Он всю жизнь прожил в Бруклине!!» и так далее. И все же история доказывает, что наука, мягко говоря, не слишком снисходительно относится к простодушной интуиции здравого смысла. Философы Патриция и Пол Черчленд предлагают нам представить, как аргумент Серля можно использовать против теории Максвелла о том, что свет состоит из электромагнитных волн. Человек держит в руке магнит и машет им вверх-вниз. Человек создает электромагнитное излучение, но никакого света не видно; следовательно, свет – это не электромагнитные волны. Мысленный эксперимент замедляет волны до такого диапазона, при котором мы, люди, уже не видим их как свет. Доверяя своему восприятию в ходе мысленного эксперимента, мы можем прийти к ложным выводам о том, что быстрые волны тоже не могут быть светом92. Серль аналогичным образом свел мысленные вычисления к тому скоростному диапазону, в котором мы, люди, уже не воспринимаем его как понимание (ведь понимание обычно происходит гораздо быстрее). Доверяя своей интуиции во время мысленного эксперимента, мы приходим к ложному заключению о том, что быстрое вычисление тоже не может быть пониманием. Если бы ускоренная версия нелепой истории, предложенной Серлем, стала реальностью, и мы бы встретили человека, который производил впечатление свободно общающегося на китайском языке, но на самом деле за доли секунды осуществлял бы миллионы мысленных операций в соответствии с выученными правилами, неясно, стали ли бы мы отрицать, что он понимает по-китайски.
Мое личное мнение – что Серль просто исследует факты, связанные с английским словом understand («понимать»). Люди не хотят использовать это слово, если ситуация не характеризуется определенными стереотипными условиями: правила языка используются быстро и неосознанно, а содержание языка связано с убеждениями человека как единого целого. Если люди отказываются описывать этим повседневным словом экзотические условия, разрушающие стереотип, но при этом сохраняющие суть этого явления, то с научной точки зрения мы ничем особенно не рискуем. Можно подобрать другое слово или условиться использовать старое слово в специальном значении, какая разница! Трактовка того, как устроено понимание, останется той же. В конце концов, цель науки – исследовать устройство вещей, а не определять, какие из этих вещей «действительно» являются примерами знакомого всем слова. Если какой-нибудь ученый объясняет функционирование локтевого сустава человека, говоря, что это рычаг второго рода, что за опровержение будет, если мы попросим представить человека, держащего в руке рычаг второго рода, и заявим: «Посмотрите, ведь у этого человека не три локтя\\»
Что касается «физико-химических свойств» мозга, я уже обозначил основную проблему: опухоли мозга, мышиные мозги, нервные ткани в пробирке понимать не могут, но их физико-химические свойства остаются такими же, как и у нашего мозга. Вычислительная теория так объясняет различие: эти куски нервной ткани не образуют структуру связей, нужную для данного типа обработки информации. Например, у них нет компонентов, которые отличают глагол от существительного; их модели деятельности не рассчитаны на соблюдение правил синтаксиса, семантики, здравого смысла. Конечно, это всегда можно назвать различием в физико-химических свойствах (в том же самом смысле, в котором две книги различаются своими физико-химическими свойствами), но тогда этот термин будет бессмысленным, потому что он уже не будет определяться языком физики и химии.
В том, что касается мысленных экспериментов, переход на другую сторону – привычное дело. Вероятно, самый весомый контраргумент «китайской комнате» Серля мы находим в рассказе фантаста Терри Биссона, получившем широкое распространение в Интернете. Рассказ написан в форме разговора между предводителем межпланетного флота исследовательских космических кораблей и его главнокомандующим, и начинается этот диалог так:
– Они сделаны из мяса.
– Из мяса?
…
– В этом не может быть сомнений. Мы отобрали нескольких представителей из разных мест планеты, доставили их на борт нашей лаборатории и исследовали их до мельчайших подробностей. Они полностью мясные.
– Это невозможно! А как же радиосигналы? Послания к звездам?
– Они используют радиоволны для общения, но сигналы исходят не от них, а от машин.
– Так кто сделал машины? Вот с кем нам надо найти контакт!
– ОНИ сделали машины. Об этом я тебе и пытаюсь сказать. Мясо сделало машины.
– Это смешно! Как может мясо сделать машину? Ты просишь меня поверить в разумное мясо?
– Я не прошу, я говорю. Эти создания – единственная разумная раса в этом секторе, и они сделаны из мяса.
– Может, они как орфоли? Ну тот углеводный интеллект, который проходит через стадию мяса?
– Вовсе нет. Они как рождаются мясом, так мясом и умирают. Мы изучили их в нескольких поколениях, которые очень недолговечны. Как ты думаешь, сколько живет мясо?
– Не до того! Хорошо, может они только частично мясные. Знаешь, как веддили. Мясная голова, а внутри мозг из электронной плазмы.
– И снова мимо. Мы подумали об этом сразу как увидели эти мясные головы, похожие на веддилические. Но я же сказал, что мы проверили их. Они мясные целиком, сплошь.
– Ну то есть мозга нет?
– О, у них нормальный мозг. Просто этот мозг СДЕЛАН ИЗ МЯСА! Я давно уже пытаюсь тебе это сказать!
– Так… а что же думает?
– Ты что, не понимаешь? Ты не слышишь, что я говорю? Мозг думает! Мясо.
– Думающее мясо! Ты просишь меня поверить в думающее мясо!
– Да, думающее мясо! Сознательное мясо! Любящее мясо. Мечтающее мясо. Всё в мясе. Ты начинаешь понимать или мне начать все с начала?[10]93

Второй критик вычислительной теории сознания – математик и физик Роджер Пенроуз – в своем бестселлере под названием «Новый ум короля» (вот это я понимаю, сильное опровержение!) строит критику не на обращении к здравому смыслу, а на глубокомысленных вопросах логики и физики. Он утверждает, что из знаменитой теоремы Гёделя следует, что все математики – и, соответственно, все люди вообще – не компьютерные программы.
Грубо говоря, Гёдель доказал, что любая формальная система (такая, как компьютерная программа или совокупность аксиом и правил логического вывода в математике), даже умеренно эффективная (достаточно эффективная, чтобы констатировать арифметические истины) и последовательная (не порождающая противоречащих друг другу утверждений) может генерировать утверждения, которые истинны, но истинность которых не может быть доказана системой. Поскольку мы, математики, будучи людьми, можем просто увидеть, что эти утверждения истинны, мы не являемся формальными системами, как компьютеры. Пенроуз считает, что способности математика происходят от аспекта сознания, который не может быть интерпретирован как вычисление. Более того, не может он объясняться и деятельностью нейронов – они слишком велики для этого. Он не может объясняться теорией эволюции Дарвина. Он не может быть объяснен даже физикой в современном понимании этого слова. В микротрубочках, составляющих миниатюрный скелет нейронов, имеют место квантово-механические эффекты, которые должны интерпретироваться в рамках пока не сформулированной квантовой теории гравитации. Эффекты эти настолько непостижимы, что это сравнимо с непостижимостью самого сознания94.
Математический аргумент Пенроуза логики назвали ошибочным; другие его утверждения получили нелестные отзывы от специалистов в других областях, относящихся к предмету. Одна из главных проблем заключается в том, что реальные математики не обладают талантами, которые Пенроуз приписывает идеализируемому математику: такими, как уверенность в том, что система правил, на которую он полагается, последовательна. Другая проблема – в том, что квантовые эффекты почти наверняка сводятся на нет в нервной ткани. Третья – в том, что микротрубочки имеются во всех видах клеток и, по-видимому, не играют никакой роли для наличия у мозга интеллекта. Четвертая – в том, что сложно даже представить себе, как сознание может возникнуть из квантовой механики.
Аргументы Пенроуза и Серля объединяет нечто большее, чем общий противник. В отличие от теории, против которой они направлены, они имеют так ничтожно мало общего с открытием и интерпретацией явлений в научной практике, что остаются эмпирически стерильными; они не позволяют проникнуть в суть вещей и не вдохновляют на научные открытия относительно того, как работает мышление. Собственно, на самый интересный вывод, следующий из «Нового ума короля», указывает Деннетт. Выдвигая обвинения в адрес вычислительной теории сознания, Пенроуз, сам того не желая, делает ей комплимент. Вычислительная теория так хорошо вписывается в наше понимание мира, что для того, чтобы ее опровергнуть, Пенроузу приходится отвергнуть подавляющую часть современных достижений нейробиологии, эволюционной биологии и физики!95
Заменят ли нас машины?
В рассказе Льюиса Кэрролла «Что Черепаха сказала Ахиллу» быстроногий греческий воин догоняет неспешную черепаху, тем самым опровергая апорию Зенона о том, что, сколь бы малое преимущество на старте ни получила черепаха, Ахилл не сможет ее догнать. (За то время, которое потребуется Ахиллу, чтобы преодолеть это расстояние, черепаха пройдет еще небольшую часть пути; за то время, которое потребуется Ахиллу, чтобы преодолеть это небольшое расстояние, черепаха пройдет еще немного, и так до бесконечности.) Черепаха предлагает Ахиллу аналогичный парадокс из области логики. Ахилл достает из своего шлема огромный блокнот и карандаш, а черепаха диктует ему первую аксиому Евклида:
(A) Равные одному и тому же равны между собой.
(B) Две стороны этого треугольника равны одному и тому же.
(Z) Две стороны этого треугольника равны между собой.
Ахиллу приходится согласиться с тем, что любой, кто считает истинными посылки А и В и суждение «Если А и В, тогда Z», должен будет признать истинным также Z. Но теперь черепаха не соглашается с логикой Ахилла. Она говорит, что вынуждена отвергнуть заключение Z, потому что никем и никогда не было написано правило логического вывода из списка посылок, которые она должна принять. Она призывает Ахилла заставить ее признать истинность Z. Ахилл в ответ добавляет в свой блокнот суждение С:
(C) Если А и В истинны, то Z должно быть истинным.
Черепаха отвечает, что не понимает, почему она должна признать, что, поскольку истинны А, В и С, Z тоже должно быть истинным. Ахилл добавляет еще одно суждение —
(D) Если А, В и С истинны, то Z должно быть истинным —
и заявляет, что «логика возьмет вас за горло и вынудит» принять Z. Черепаха отвечает так:
«То, что мне сказала Логика, следовало бы записать, – заметила Черепаха. – Внесите, пожалуйста, в свой блокнот условное суждение, которое мы обозначим Е:
Е. «Если А, В, С и D истинны, то Z должно быть истинным».
– Согласен, – ответил Ахилл с оттенком печали в голосе.
В этот момент неотложные дела в банке вынудили рассказчика оставить счастливую пару. Лишь через несколько месяцев ему довелось снова проходить мимо того места, где беседовали Ахилл и Черепаха. Ахилл по-прежнему сидел на спине у многотерпеливой Черепахи и что-то писал в почти заполненном блокноте. Приблизившись, рассказчик услышал, как Черепаха сказала:
– Записали последнее условное суждение? Если я не сбилась со счета, оно должно быть тысяча первым. Осталось еще несколько миллионов96[11].
Решение этого парадокса, конечно же, заключается в том, что ни одна система гипотетических умозаключений не может строго следовать явно выраженным правилам. В тот или иной момент она должна, как сказал Джерри Рубин (а чуть позже – и корпорация «Найк»), «просто делать это» (имеется в виду рекламный слоган фирмы «Найк» Just do it! – Прим. пер.). Подразумевается, что правило должно просто выполняться за счет рефлекторной, грубой силы системы, без лишних вопросов. В этот момент система, если она имеет форму машины, будет не следовать правилам, а просто подчиняться законам физики. Аналогичным образом, если демоны (правила замещения одних символов другими символами) считывают и записывают репрезентации, а внутри каждого демона есть демоны еще меньше (и еще глупее), то в какой-то момент нам все же придется отказаться от их услуг, позвать охотников за привидениями и заменить самых маленьких и самых глупых демонов машинами. В случае людей и животных это будут машины, построенные из нейронов: нейронные сети. Давайте посмотрим, каким образом наша картина того, как работает мышление, подкрепляется простыми идеями о том, как работает мозг.
Первые шаги в этом направлении сделали математики Уоррен Маккалок и Уолтер Питтс, которые писали о «нейрологических» свойствах связанных между собой нейронов97. Нейроны сложны и до сих пор не объяснены, однако Маккалок и Питтс (а вслед за ними – и многие другие разработчики моделей нейронных сетей) выделяют как наиболее значимую одну из их функций. Нейроны складывают совокупность атрибутов, сравнивают полученную сумму с порогом и сигнализируют о том, превышен ли порог. Это описание того, что они делают, с концептуальной точки зрения; с физической точки зрения то же самое можно описать следующим образом: возбужденный нейрон может быть активен в разной степени, и степень активности зависит от уровня активности входящих аксонов других нейронов, присоединенных в синапсах к дендритам нейрона (входящим структурам). Синапс имеет вес, варьирующийся от положительного (возбуждающий синапс) до нулевого (без воздействия) и далее до отрицательного (тормозящий синапс). Уровень возбуждения каждого входящего аксона умножается на вес синапса. Нейрон суммирует эти входящие уровни; если сумма превышает пороговый уровень, то нейрон возбуждается и поочередно посылает сигналы всем нейронам, соединенным с ним. Хотя нейроны всегда находятся в возбужденном состоянии, и входящие сигналы только заставляют их возбуждаться заметно быстрее или медленнее, иногда бывает удобно говорить о них как о неактивных (низкий уровень возбуждения) и активных (высокий уровень).
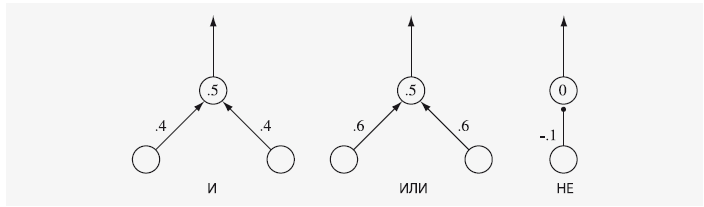
Маккаллок и Питтс показали, каким образом эти модельные нейроны, будучи связаны между собой, образуют логические вентили. Логические вентили реализуют отношения фундаментальных логических операций, лежащих в основе простых умозаключений: «и», «или», «не». Суждение «А и В» (на концептуальном уровне) истинно только тогда, когда истинно А и истинно В. Вентиль И (на механическом уровне) выдает единицу на выходе, только если есть сигнал на обоих входах. Чтобы сделать логический вентиль из модельных нейронов, нужно установить порог выходного узла на величину больше веса каждого из входов, но меньше их суммы, как показано на рисунке мини-сети слева внизу. «А или В» (на концептуальном уровне) истинно, если истинно А или истинно В. Логический вентиль ИЛИ (на механическом уровне) выдает сигнал на выходе, если есть сигнал хотя бы на одном из входов. Чтобы получить единицу на выходе, нужно установить порог на величину меньше веса каждого из входов, как показано на схеме мини-сети внизу посередине. Наконец, утверждение «не А» (на логическом уровне) истинно, если ложно А, и наоборот. Логический вентиль «НЕ» выдает единицу на выходе, когда на входе ноль, и наоборот. Чтобы получить единицу, нужно установить порог равным нулю, чтобы нейрон возбуждался, получая на входе ноль, а вес входа сделать отрицательным, чтобы входной сигнал выключал нейрон, как на схеме минисети внизу справа.
Предположим, что каждый из модельных нейронов отображает простое суждение. Мини-сети можно соединить между собой таким образом, чтобы выход одной сети поступал на вход другой, с целью оценить истинность сложного суждения. Например, нейронная сеть может оценивать суждение {[(X жует жвачку) и (у X раздвоенные копыта)] или [(у X есть плавники) и (у X есть чешуя)]}, суммирующее признаки, которыми должно обладать животное, чтобы оно считалось кошерным. Собственно, если сеть модельных нейронов соединить с любым видом расширяемой памяти (например, с рулоном бумаги, над которой размещены штамп и ластик), то получится машина Тьюринга, полноценный компьютер.
И все же абсолютно непрактичным было бы представлять суждения или даже составляющие их концепты в виде логических вентилей, независимо от того, из чего состоят эти логические вентили – из нейронов или из полупроводников. Проблема в том, что каждый концепт и каждое суждение в этом случае должно быть заранее встроенным в виде отдельного узла. На деле и компьютер и мозг представляют концепты в виде моделей действий, совершаемых над совокупностями единиц. Простой пример – скромный байт, который в каждом компьютере используется для репрезентации буквенноцифровых символов. Форма репрезентации буквы В – 01000010, где каждая цифра (бит) соответствует одному из крохотных кусочков кремния, выложенных в ряд. Второй и восьмой кусочек заряжены, что соответствует единицам, а остальные – не заряжены, что соответствует нулям. Построить байт можно и из модельных нейронов, при этом схема распознавания шаблона буквы В будет организована по принципу простой нейронной сети:
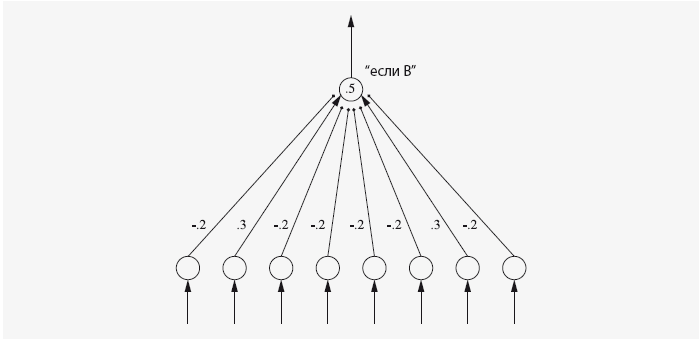
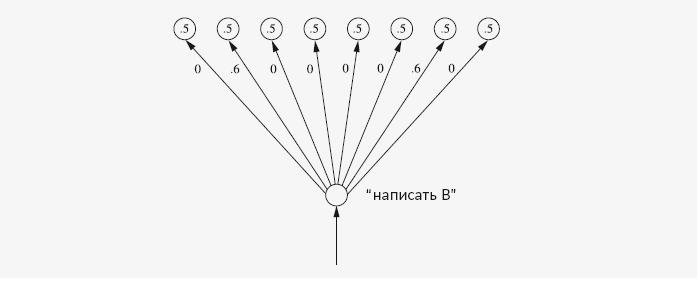
Несложно представить, что эта сеть – одна из составляющих частей демона. Если нижний ряд модельных нейронов присоединить к краткосрочной памяти, то верхний нейрон будет определять, содержатся ли в краткосрочной памяти экземпляры символа В. А на странице 118 изображена сеть той части демона, которая записывает в память символ В98.
Мы уже на пути к тому, чтобы создать из модельных нейронов условную цифровую вычислительную машину; но давайте немного отклонимся от курса и сделаем более биоморфный компьютер. Во-первых, мы можем сделать так, чтобы наши модельные нейроны следовали не классической логике, а нечеткой логике. Во многих сферах у людей нет однозначных убеждений касательно того, истинно данное суждение или ложно. Бывает так, что о предмете сложно сказать, принадлежит он к данной категории или нет, скорее можно говорить о том, что он более удачный или менее удачный пример данной категории. Возьмем категорию «овощи». Большинство людей согласятся с тем, что сельдерей – это полноценный овощ, а чеснок – не очень хороший пример.
А если верить администрации президента Рейгана, пытавшейся оправдать урезанное финансирование школьного питания, овощем можно считать даже кетчуп (хотя после обрушившейся на эту программу критики администрация была вынуждена признать, что кетчуп – не очень хороший пример). На концептуальном уровне мы воздерживаемся от однозначных заявлений о том, является ли данный предмет овощем или нет, и предпочитаем говорить, что этот предмет – более удачный или менее удачный пример овоща. На механическом уровне мы уже не утверждаем, что узел, представляющий «овощность», должен быть включен или выключен, а допускаем варьирование значения, которое может составлять от 0 (для камня) и 0,1 (для кетчупа) до 0,4 (для чеснока) и 1,0 (для сельдерея).
Мы можем также отказаться от произвольно выбранного кода, связывающего каждый концепт с бессмысленной последовательностью битов. Пусть каждый бит сам представляет какой-нибудь элемент концепта. Скажем, один будет представлять зеленый цвет, другой – наличие листьев, третий – хрусткость, и так далее. Каждый из этих узлов, представляющих свойства овощей, может быть присоединен с небольшим значением веса к самому узлу, представляющему овощ. Другие узлы, представляющие характеристики, которых у овощей нет (такие, как «магнитный» или «мобильный»), могут быть присоединены с отрицательными значениями веса. На концептуальном уровне чем больше качеств овоща есть у данного предмета, тем более удачным примером овоща является этот предмет. На механическом уровне чем больше узлов качеств овоща срабатывают, тем выше уровень активации узла, представляющего овощ.

