 0
0Los problemas de matemática en la práctica didáctica
Se trata de crear un contexto emocional positivo que debe ser estable a nivel cognitivo y relacional (ver la experiencia narrada en D’Amore, Giovannoni, 1997).
En resumen, es obvio que la emoción que no se relaciona con hechos contingentes y raros modifica el sistema mismo de convicciones y valores (sobre este punto, ver Pellerery y Orio, 1996): las reacciones emocionales repetidas llevan a asumir comportamientos; nos parece que un resultado positivo se puede obtener si el estudiante está dispuesto a modificar el modelo mismo de expectativa estándar de la Matemática por un modelo no estándar que el profesor le da como alternativa (repetimos: no de manera episódica, sino de manera estable en cuanto al tiempo y a la motivación).
Lo anterior nos lleva necesariamente a una reflexión sobre los comportamientos frente a la Matemática.
Recuerdo aquí los estudios pioneros de Aiken (1970, 1976), en los cuales se distinguieron los momentos cruciales del nacimiento de un comportamiento negativo en relación con la Matemática en la franja escolar que corresponden a los grados de 6 hasta 8 (es decir más o menos alumnos entre los 11 y los 14 años de edad). Aquí se trata de revertir el fenómeno buscando, en la medida de lo posible, comportamientos positivos. Ahora bien, existe un Inventario de comportamientos con relación a la matemática de Sandman (1980) que incluye seis escalas de medida:
• el placer de hacer Matemática
• el valor dado a la Matemática
• la percepción del profesor de Matemática
• la ansiedad con respecto a la Matemática
• el auto concepto en el quehacer matemático
• la motivación para hacer Matemática.
El hecho que los valores mínimos se alcancen en el paso de la primaria a la escuela sucesiva, e incluso que tales valores se vuelvan negativos propiamente entre los grados 6 y 8, además de ser evidente ante los ojos de cualquier profesor e investigador, es confirmado por algunos estudios, por ejemplo los de Anderman y Maehr (1994); lo anterior se adhiere al rechazo, a la aversión, a la motivación negativa, al negarse a creer que la construcción personal de la Matemática es una posibilidad: una especie de autodefensa de un “monstruo” que no se puede controlar de ninguna manera.
El interés investigativo e incluso el interés solo pedagógico en este sentido se debe centrar, más que en los procesos de la enseñanza, en los procesos del aprendizaje; mejor aún, debe centrarse en la relación enseñanza/aprendizaje partiendo de las siguientes convicciones, tal como se presentan en D’Amore y Frabboni (1996):
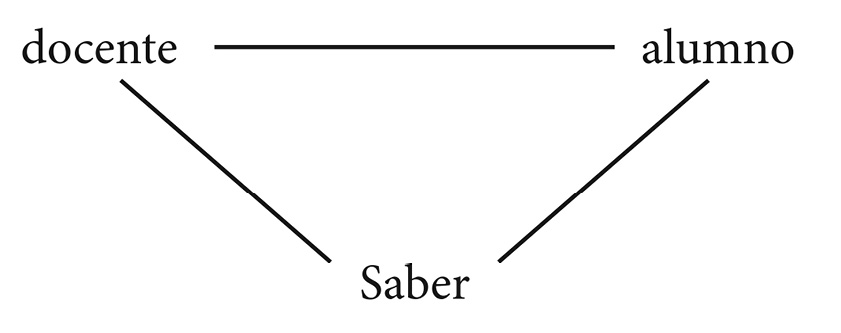
• el sujeto de la enseñanza de la Matemática no es la Matemática misma sino el alumno y, por lo tanto, la atención del profesor debe estar concentrada en los alumnos que están aprendiendo Matemática; de tal manera, se vuelve vital reconsiderar cada vez y tener siempre presentes todas las implicaciones incluidas en el triángulo de la Didáctica (Chevallard, 1985);
• el aprendizaje no se mide a través de una “cantidad de competencias adquiridas” vagas e indefinidas, se mide sobre todo a partir del placer, el deseo y la disposición a usarlas;
• la motivación intrínseca para aprender se debe mostrar como un objetivo didáctico, no como una condición de inicio (D’Amore, Sandri, 1994);
• en la enseñanza de la Matemática es necesario respetar al individuo; en este punto se sitúa la intención de no forzar aprendizajes vacíos o meramente formales, sino la necesidad de construir el pensamiento matemático, con la colaboración continua y cercana del alumno mismo, inclusive con la intención de dejar en él recuerdos positivos (no solo de orden cognitivo) de la materia (ver Furinghetti, 1993);
• en el proceso aprendizaje/enseñanza de la Matemática hay que considerar como algo prioritario que se debe tener siempre bajo observación la imagen que tanto el profesor como el alumno tienen de la Matemática, la imagen que tiene el alumno de sí mismo cuando hace Matemática y también la imagen que tiene el profesor de sí mismo en el desempeño de su rol.
Nota bibliográfica
Para la redacción de esta sección, hice uso de (Aiken, 1970, 1976; Anderman, Maehr, 1994; Boero, 1986; Bruner, 1961; Chevallard, 1985; Cornoldi, Caponi, 1997; D’Amore, 1994a, 1995a; D’Amore, Frabboni, 1996; D’Amore, Giovannoni, 1997; D’Amore, Martini, 1997b; D’Amore, Oliva, 1994; D’Amore, Sandri, 1994, 1996; Franta, 1993; Furinghetti, 1993; Hadamard, 1993; Hart, 1985; Heckhausen, 1990; Kruteskii, 1976; Kuhl, 1984; Laborde, 1982, 1995; Maier, 1993; Pellerey, 1992; Pellerey, Orio, 1996; Poincaré, 1906, 1914; Sandman, 1980; Zan, 1995, 1997).
De manera particular, sobre la distinción entre motivación y volición ver (D’Amore, 2003; D’Amore, Fandiño Pinilla, 2012; D’Amore, Godino, Arrigo, Fandiño Pinilla, 2003; Fandiño Pinilla, 2006; Pellerey, 1993).
A propósito de la motivación externa al aprendizaje de la Matemática, la educación de la intuición y la superación de los estereotipos escolares puede ser muy fructífero el estudio de las investigaciones de G. B. Saxe; quien, en efecto, hace mucho tiempo estudia situaciones de aprendizaje de la Matemática fuera del mundo escolar y, de tal manera, ha logrado comparar el aprendizaje escolarizado y el no escolarizado, obteniendo resultados interesantísimos. Sugiero (Saxe, 1977, 1979, 1982, 1985). Sobre todo, en lo relacionado con nuestro tema (Saxe, 1988). Para el lector poco familiarizado con las búsquedas bibliográficas (Saxe, 1991).
Un estudio critico – analítico del triángulo de la Didáctica en (D’Amore, Fandiño Pinilla, 2002.
2.4. El contrato didáctico en el laboratorio
Una sección breve para decir solo que: si al menos parte de la actividad escolar de la Matemática se desarrolla en el laboratorio, el contrato didáctico cambia porque cambian la motivación, el interés, el comportamiento y la volición.
Como lo dije anteriormente (con varios ejemplos de “casos”) la figura del profesor que da o promueve problemas es distinta solo si en cambio del ambiente de clase se trabaja en un ambiente distinto, un especifico ambiente de laboratorio, por varios motivos. Esto depende de varios factores, entre los que el “hacer” tiene un rol privilegiado, más que el “escribir” o el “hablar”. Las situaciones problemáticas que se delinean en el laboratorio se relacionan muchas veces con algo que se debe construir, hacer o manejar en la práctica, concretamente; para cuya realización se deben superar no solo obstáculos conceptuales sino también obstáculos prácticos y concretos. La ayuda del profesor (o del “técnico del laboratorio”, cuando existe) es esencial y significativa. La motivación que nace de esta actividad puede ser diferente y muy productiva: al final hay un producto funcional, un objeto que se puede mostrar; no solo un simple resultado o una simple aceptación social, existe la posibilidad de mostrar con orgullo un objeto, algo que funciona y que tiene un sentido.
Lo anterior me lleva consecuentemente al problema de la operatividad:
• en el laboratorio se puede pensar en un reto o en una simulación de la realidad en términos reales;
• en clase, la simulación del laboratorio no logra ser convincente (tan solo como modalidad ficticia); a lo cual yo llamo extrañamiento del ambiente o identificación artificial.
El origen de muchas de las molestias que produce el simple acercamiento a la Matemática es precisamente no querer distinguir lo real de lo ficticio. El mero acercamiento a la formalización de lo real puede generar un rechazo que, paradójicamente (valdría la pena reflexionar) es más acentuado en los estudiantes más “listos”. Cito aquí el caso de una niña de cuarto grado, J.; J. es muy lista en todas las asignaturas, sobre todo en idiomas y en dibujo; la niña demuestra creatividad, sabe hablar y contar historias, comprende los textos inmediatamente, es espontánea y activa; en Matemática es muy rápida, pero no participa activamente en la resolución de ejercicios ni en la ejecución de operaciones. Apenas se acerca a la descripción de una situación problemática, aún más si la situación es real, J. se cierra y no muestra disposición para escuchar, rechaza el contacto con la formalización y manifiesta incomodidad y poca tolerancia.
¿Qué se puede hacer en este caso? No se trata de una manifestación aislada, aún si en este caso se manifiesta de manera macroscópica; hay que “enmascarar” las situaciones problemáticas de carácter matemáticos, lo que puede pasar con:
• decir que se trata de otra cosa, no de Matemática;
• recurrir al laboratorio, donde el lenguaje puede no ser formal (puede estar relacionado con el dibujo u otra labor concreta).
Nota bibliográfica
Para la redacción de esta sección, utilicé (D’Amore, 1990-91; Fischbein, Vergnaud, 1992).
Las referencias bibliográficas generales para todo el capítulo son aquellas relativas al estudio de la relación comunicativa que pasé por alto para no hacer demasiado pesado el texto. Me limito a algunas referencias significativas: (Caroni, Iori, 1989; Argyle, 1974; Coffman, 1971; AA. VV., 1978).
Para el tema de la enseñanza vs. aprendizaje, una visión unitaria de proceso de interacción, ver (Postic, 1979).
Sobre el tema de las interacciones verbales profesor/alumno existen cientos de técnicas diversas, tal y como lo expone el clásico (Ballanti, 1984).
Entre las técnicas de interacción verbal, me parece aún interesante el modelo de Amidon-Hunter (el cual perfecciona sustancialmente el modelo precedente de Flanders), muy complejo y variado; ver (Amidon, Hunter, 1983).
Actualmente, en este campo, es indispensable poner atención a la llamada “interacción no verbal” (examinada en una fase especial por nosotros, la fase en la que los niños de una clase resuelven problemas dados por un experimentador, en presencia tanto de éste como del profesor); ver (Kaes, Anzieu, 1981; Kaes, 1983; AA. VV., 1974; AA. VV., 1985).
5 El autor de este pasaje (Pellerey, 1993) se refiere a los célebres trabajos de Kuhl (1983, 1984) sobre los procesos que preceden la realización de nuestras intenciones.
6 Ciertamente, hay que examinar si no es banal solo el “paso”, o también los dos “polos”: el deseo y la realización. Pero este punto debo pasarlo por alto, dejando en las manos de los más expertos la tarea de continuar.
Конец ознакомительного фрагмента.
Текст предоставлен ООО «ЛитРес».
Прочитайте эту книгу целиком, купив полную легальную версию на ЛитРес.
Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.
Вы ознакомились с фрагментом книги.
Для бесплатного чтения открыта только часть текста.
Приобретайте полный текст книги у нашего партнера:
Полная версия книгиВсего 10 форматов

