
Bir Nefeste Matematik
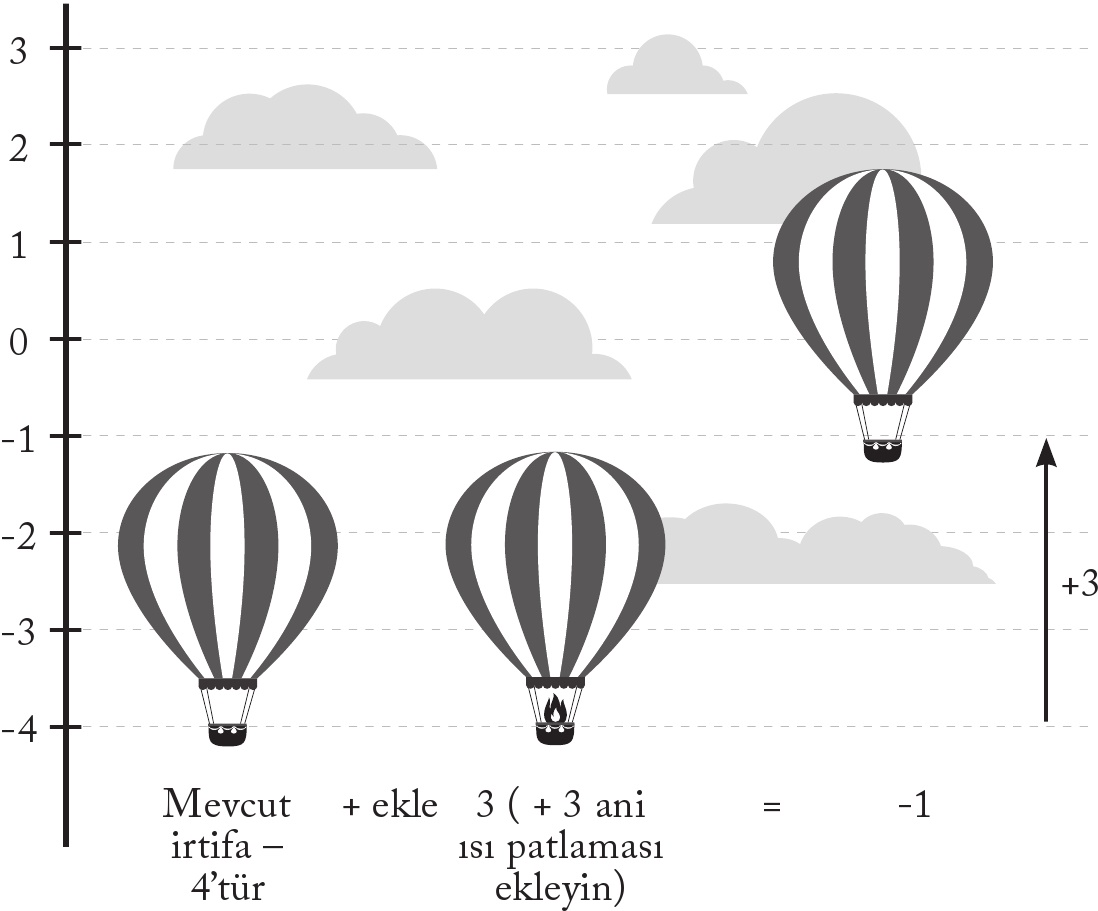
Burada balon sayı doğrusunda üç sıra yükselip – 4’ten – 1’e çıkacaktır1. Bu yüzden – 4 + 3 = – 1 olur.
İçinde bir sürü negatifin bulunduğu birazcık daha hileli bir örnek – 1 – – 6 olacaktır ve şu şekilde yorumlayabiliriz:
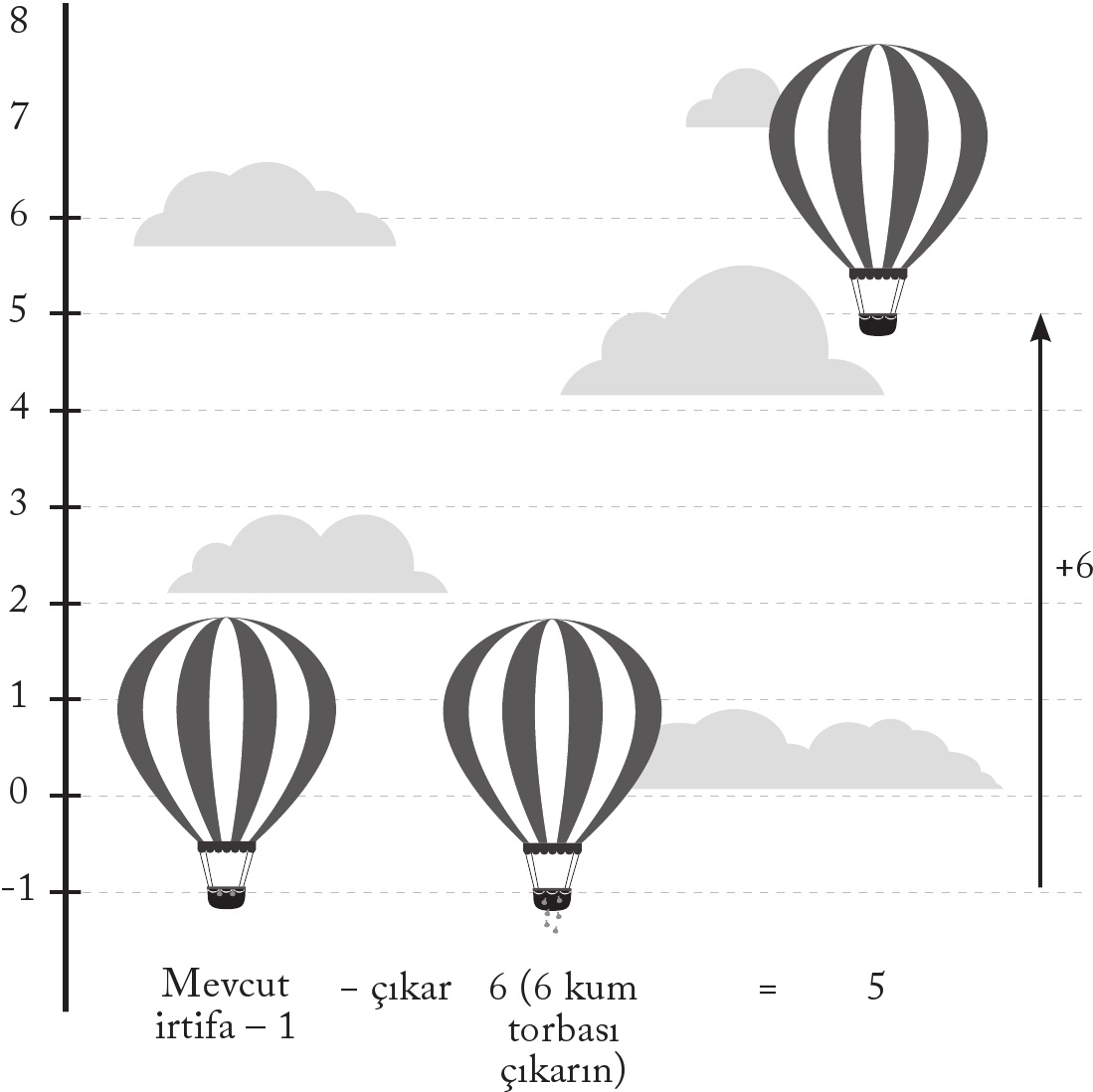
Altı kum torbasının sepetin kenarından atılması balonun altı basamak yükselmesine neden olur, böylece – 1 – – 6 = 5.
Mademki balonumuzun ne zaman yükselip ne zaman alçalacağını biliyoruz artık daha karmaşık aritmetik hesaplara ve dört işlemin geri kalanına bakabiliriz.
4. Bölüm
TOPLAMA VE ÇARPMA
Konu daha büyük sayıları kâğıt üstünde toplama işlemi olduğunda kullandığımız yöntemlerin hepsi basamak değeri ile sayıya kodlanan bilgiye dayanmaktadır. Bildiğimiz üzere 1234 rakamları ile bin iki yüz otuz dört sayısı temsil edilmektedir. Bunun nedeni ise sayıdaki her bir basamağın buna karşılık gelen bir değeri olmasıdır. Bunlar sağdan başlayarak birler (genellikle bu şekilde isimlendirilir), onlar, yüzler, binler, on binler vs. biçimindedir ve sola doğru ilerledikçe her basamakta on kat büyürler. Bu sebeple 1234 sayısı dört tane bir (4), üç tane on (30), iki tane yüz (200) ve bir tane bin (1000) içerir. Yani 1234’ü şu şekilde yazabilirim;
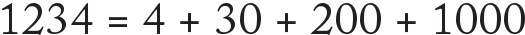
Buna matematik öğretmenleri tarafından “uzatılmış biçim” adı verilmektedir ve toplamaların nasıl işlediğini anlamakta gerçekten işe yaramaktadır. Örneğin 1234 + 5678’i düşünün. Şayet her bir sayıyı uzatılmış biçimde yazarsam:

Her bir eşleşen basamak değerini kolayca birlikte toplayabilirim:

Buradan 1234 + 5678 = 12 + 100 + 800 + 6000 = 6912 olduğunu anlayabilirim.
Okulda bize öğretilen yöntem ise bu sürecin kısaltılmış biçimiydi. Birbirine karşılık gelen basamakları alt alta yazıp sağdan sola doğru topluyoruz:
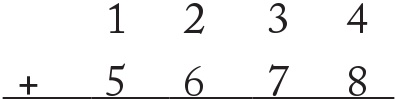
İlk toplama işlemi 4 + 8 = 12 olur. Tek basamaklı yanıt kutusuna 12 yazamayız ancak 12 = 10 + 2’dir bu yüzden 2’yi bu kutuda bırakıp 10’u bir sonraki hesaplamaya taşırız.
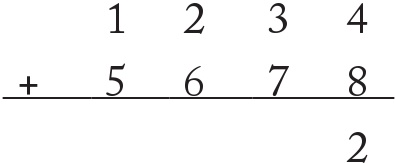
Teknik olarak bir sonraki basamağın toplamı 10 + 30 + 70 = 110’ dur, ancak burada onlar basamağında işlem yaptığımız için kaç tane onumuz olduğuna bakmalıyız; toplamda 1 + 3 + 7 = 11 tane onumuz vardır. Bu yüzden yine bu basamağa sığamayacak kadar rakamımız bulunmaktadır. 11 = 10 + 1, yani onlar basamağına bir tane 1 yazıp diğer 1’i yüzler basamağına taşırız:
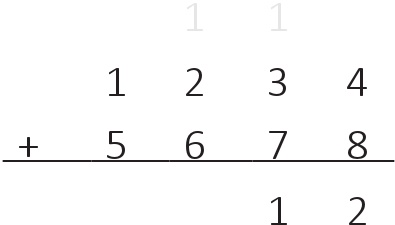
100 + 200 + 600 = 900:
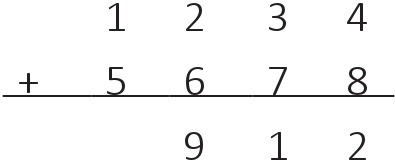
Ve son olarak da 1000 + 5000 = 6000:

Çarpma işlemi ise tekrarlayarak toplama işlemi yapmanın hızlı bir yoludur. 12 × 17 sorusu aslında “On iki çarpı on yedi kaç eder?” diye sormaktadır. Yanıtı on iki tane on yediyi ya da on yedi tane on ikiyi toplayarak bulabilirim; ancak çarpım tablosunu önceden öğrenmişseniz çarpma işlemi çok daha hızlıdır.
Elimde birçok marka olduğunu düşünün. 12 × 17 problemini her biri on yedi tane marka içeren on iki sıra oluşturarak ve sonra da bunları toplayarak çözebilirim:

Bununla birlikte şayet 12’yi 10 + 2 ve 17’yi de 10 + 7 olarak düşünürsem, o halde markaları şu şekilde gruplandırabilirim:

Çarpım tablosunu bildiğim için her bir alt bölümde kaç tane markanın olması gerektiğini biliyorum:

Dolayısıyla 12 × 17 = 100 + 70 + 20 + 14 = 204 olduğunu artık biliyorum. Bu yönteme (204 markayı çıkarma) “ızgara yöntemi” adı verilir. Şimdi ise 293 × 157 problemini çözmek için biraz daha gelişmiş bir modeli görelim:

Muhtemelen bütün bu çarpma işlemlerini, özellikle çarpım tablomuzdaki sayılardan çok büyük olan bu sayılar için nasıl kafamdan yaptığımı merak ediyorsunuzdur. Aslında çok havalı bir hilesi var. Herhangi bir tam sayıyı on ile çarptığım zaman sayının sonuna bir sıfır ekliyorum. Yani 100 × 200 için 100’ün 1 × 10 × 10 ve 200’ün de 2 × 10 × 10 olması gerektiğini biliyorum. Bunların hepsini bir araya getirirsem:
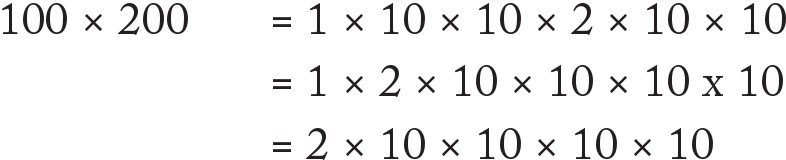
Basamak değerinin tasarımının her iki yönde de genişletilebileceğine dikkat etmek gerekir. Birler basamağından sağa doğru ilerledikçe her adımda basamak değeri on kat düşer ve onlar, yüzler, binler vs. basamağı elde ederim. Artık en sağdaki basamağın birler olmadığını göstermek adına bir ondalık virgülü kullanıyorum. Bu da ondalık sayıları veriyor. Burada, örneğin 45,3 + 27,15’i toplamak için yukarıdakiyle aynı kuralları kullanabilirim:

45,3’ün sonuna basamakları eşleştirip toplamayı daha belirgin bir şekilde yapmak üzere bir sıfır eklediğime dikkat ediniz (bu durum, özellikle çıkarma işlemi için önemlidir). Bunu 45,3 ile 45,30 aynı olduğu için yapabiliyorum: üç tane ona, sıfır tane yüz eklediğimizde sonuç hâlâ üç tane ondur. Bu yüzden matematikçiler 45,30 için kırk beş virgül otuz yerine kırk beş virgül üç sıfır ifadesini kullanırlar.
Her bir × 10’un, 2’den sonra bir sıfır anlamına geldiğini hatırlayacak olursam 100 × 200 = 20000 sonucunu elde ederim. Ne zaman bir ızgara çarpımı yapsam bu sürecin tamamını gerçekleştirmiyorum. Sadece ilk basamakları çarpıp daha sonra hesaplamada ne kadar çok sıfır varsa bunun sağına ekliyorum. Bu yüzden 50 × 200 için düşünce yöntemime göre 5 × 2 = 10 ve daha sonra üç tane sıfır eklemeliyim. Böylece 50 × 200 = 10000. Tam isabet!
Izgarama geri dönecek olursam, her bir basamağı topladığımı görebilirsiniz. Nihai yanıtım 31400 + 14130 + 471 olacaktır ki bunu da toplayacak olursak:

Son olarak cevap: 293 × 157 = 46001 olur.
Uzun çarpım yöntemi dahil olmak üzere başka yöntemleri de vardır ancak işe yarar bir yönteminiz varsa bırakmayın sakın. Şimdi toplama ve çarpmanın çok yakın dostları çıkarma ve bölmeye geçelim.
Napier’in KemikleriJohn Napier (1550-1617), çarpma işlemi için Napier’in kemikleri olarak bilinen bir dizi çubuk icat eden İskoçyalı bir matematikçi, gökbilimci ve simyacıydı. Bu sistem her bir çarpım tablosu için bir çubuk içeriyordu. Örneğin 3 için çarpım tablosu çubuğu şu şekilde olacaktır:

Örneğin, şayet 9 × 371’i hesaplamak istiyorsanız üç, yedi ve bir için çarpım tablosu çubuklarını yan yana koyup dokuzuncu sıraya kadar okuyorsunuz ki bu da şu şekilde görünür:
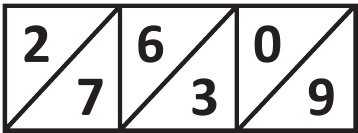
Daha sonra sağdan başlayarak her bir çapraz çizgideki sayıları topluyorsunuz. Şayet toplam dokuzdan büyükse bir sonraki çizgiye devam ediyorum:

Böylece 9 × 371 = 3339 eder.
Napier’in sihirbazlığa merak saldığı üzerine söylentiler vardı. Belirli aralıklarla hizmetçilerine, içinde bir kuş bulunan bir odaya yalnız başına girmelerini ve kuşu okşamalarını emredermiş. Kuşun onların sadakatini hissettiğini de söylermiş. Aslında Napier kuşun tüylerine is sürermiş. Vicdanen suçluluk hissedenler kuşu okşamazlar ve ellerine is bulaşmadan dışarı çıkarlarmış. Böylece de kurnaz Napier tarafından suçlu bulunurlarmış.
5. Bölüm
ÇIKARMA VE BÖLME
Çıkarma işlemi toplama ile çok benzer biçimde gerçekleştirilir. Örneğin 6543 – 5678 şöyle hesaplanır:

Buradan ise – 5 + – 30 + – 100 + 1000 = – 135 + 1000 = 865 sonucuna ulaşırım. Yine basamak yöntemimizi kullanabilirsiniz ancak toplamada bir basamakta çok fazla sayı olmasını önlemek için kullandığımız diğer basamağa taşıma sisteminin tersine ihtiyacımız var. Daha önce yaptığım gibi devam edecek olursam:
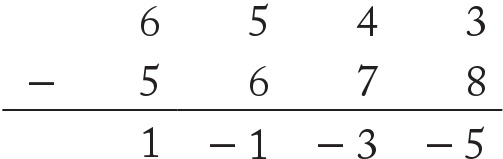
Pek de mantıklı görünmüyor, değil mi? Burada ödünç almaya ihtiyaç duyuyorum. Aslında öğrencilerimden birinin işaret ettiği üzere ödünç alınan miktar asla geri dönmediği için bu işlem için çalmak çok daha doğru bir kelime olacaktır.
3 – 8’in bir negatif sayı verdiğini fark ettiğimde bir sonraki basamaktan ödünç alarak 3’ü artırıyorum. Soldaki basamaktaki 4’ün üstünü çizip onun değerini bir düşürüyorum. Ödünç almış olduğum “bir” aslında on değerinde olduğu için birler basamağındaki 3 aslında 13’e yükselir. Böylece 13 – 8 =5 olur:

Bir sonraki basamak da 3 – 7 = – 4 şeklinde negatif bir sonuç verecektir. Yine kapı komşusu yüzler basamağından bir ödünç alırım. Yüzün değeri on tane on olduğu için elimdeki 3 tane onu 13 tane ona yükseltir böylece şu şekilde devam edebilirim:

Ancak devam etmeden önce yüzler basamağı için de bir başka ödünç alma işlemine ihtiyacım var ve görünüşe bakılırsa binler basamağımın değeri sıfıra düşecektir:
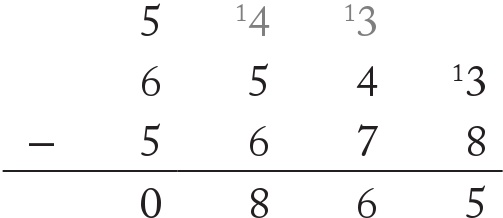
Böylece 6543 – 5678 = 865 olduğunu anlayabiliriz.
Önceki bölümde toplama ile çarpmanın birbiriyle yakından bağıntılı olduğunu görmüştük. Benzeri, çıkarma ve bölme için de geçerlidir. 3780 ÷ 15 işlemi bize aslında “3780’de kaç tane on beşin olduğunu” yani “3780’den kaç kez on beşin çıkarılabileceğini” sormaktadır. Aslında bu düşünce biçimi yığma adı verilen bir bölme yönteminin anahtarıdır. Bu yöntemde sıfıra ulaşana dek bölenin katlarını çıkarmayı sürdürüyorum.
2 × 15 = 30 olduğunu buradan da 200 × 15’in de 3000 olması gerektiğini biliyorum. Bunu 3780’den çıkararak başlıyorum:
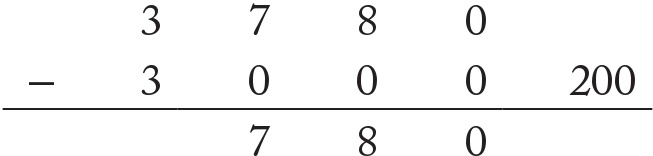
Buradan elimde 780 kalır. 4 × 15 = 60 yani 40 × 15 = 600 eder. Daha sonra bunu da çıkarırım:
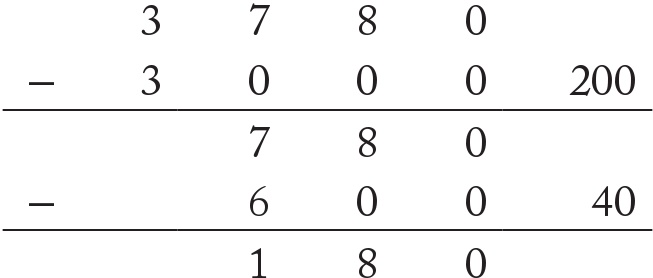
Son olarak on iki tane daha on beşi iki işlemle çıkarırım:

Artık 200 + 40 + 10 + 2 = 252 tane 15 çıkardığımı biliyorum. Yani 3780 ÷ 15 = 252 olur. Çarpmada ne kadar iyiyseniz burada o kadar az sayıda yığın alma basamağından geçebileceğinizi anlayabilirsiniz.
Çok korkulan uzun bölme (kalanlı bölme) yöntemi de çok benzer ilkelerle çalışmaktadır. Burada problemi otobüs durağı ismini verdiğim bir düzende kurguluyorum:

Soldan başlıyorum. 15 sayısı iki haneli olduğu için 3 ve 7’ye bakıyorum – 37 sayısında kaç tane 15 vardır? İki kez. Bu da bize 30’u verir ve sonra geriye kalanı çıkarma işlemini kullanarak hesaplıyorum:
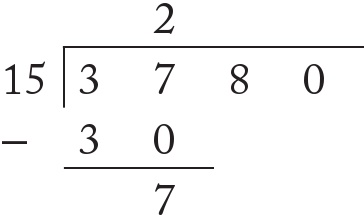
Dikkatimi şimdi elde ettiğim 7’ye ve bu 7’nin yanına yazacağım 8’e çeviriyorum. 78’de kaç tane on beş var? Bildiğim kadarıyla beş tane on beş 75 eder:
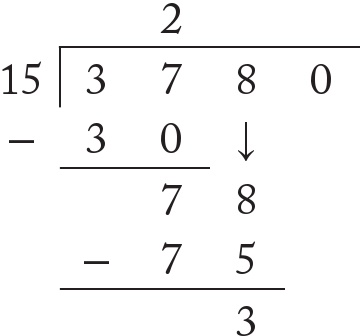
Son olarak sıfırı elde ettiğim sayının yanına indiriyorum ve 30 sayısında kaç tane on beşin bulunduğuna dikkat ediyorum:

Kısa bölme işlemi de tıpkı uzun bölme gibidir ancak tek farkı kalanları kafamızdan hesaplayıp bunları elde sayıları olarak yazarız. Kısa bölme işlemi kesirleri ondalık sayılara çevirmekte kullanışlıdır. Şayet

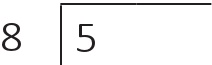
Sekiz sayısı 5’in içinde sıfır kez vardır ve geriye 5 kalır. Bu geriye kalanı bir ondalık virgülü ve bir başka sıfır yazana dek koyabileceğim herhangi bir yer yoktur. Bunu yapabiliyorum çünkü 5 = 5,0 ve buna karşılık gelen bir sıfırı yukarı yazıyorum:

50 içinde 8 ise 6 kez vardır ve kalan da 2’dir (ondalık virgülden sonra gerektiği kadar sıfır ekleyebilirim):
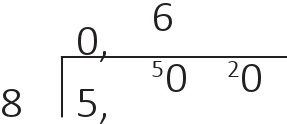
20 içinde 8 ise iki kez vardır ve geriye 4 kalır:

Ve 40 sayısında ise tam olarak beş tane sekiz vardır:
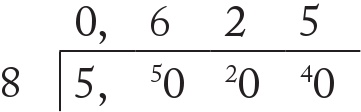
Yani artık

6. Bölüm
BAYAĞI KESİRLER VE ASAL SAYILAR
Bir bayağı kesrin nasıl ondalık sayı olarak ifade edildiğini az önce öğrendik. Şimdi

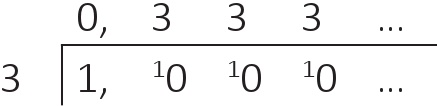
Hemen bir döngünün gerçekleştiğini fark ediyoruz; on sayısında üç, üç kere vardır ve geriye bir kalır ve bu durum sonsuza dek tekrarlanır. Bu durumun görüldüğü ondalık sayılara tekrarlanan denir ve tekrar eden hanenin üstüne bir devir çizgisi ekleriz:

Durum yedide bir için çok daha ilginç bir hal alır:
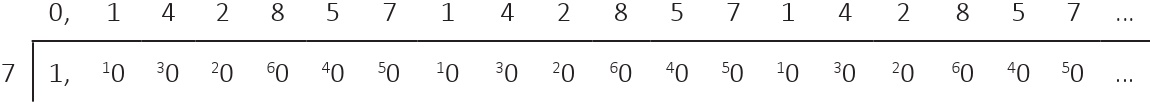
Burada elimde tekrarlanan bir haneler dizisi bulunmaktadır. Bunu tüm dizinin üstüne bir devir çizgisi ekleyerek gösterebilirim:

Dahası paydası 7 olan diğer kesirler de benzer diziyi kullanır, yalnızca farklı başlangıç ve bitiş noktalarına sahiptir.

Canınız biraz daha zorlu bir şey çektiyse dokuzları bir deneyin!
Bir bayağı kesrin paydasına bakarak tekrarlayıp tekrarlanmayacağını söyleyebilirim. Paydayı alıp onun katlarını (10, 100, 100 vs.) elde etmek üzere herhangi bir şeyle çarpabilirim. Şayet yapabiliyorsam dönüştürdüğümde ondalık sütunlarda sorunsuzca yerleşmesini sağlayabilirim.
Bunu yapmadan önce denk kesirler adı verilen çok önemli bir matematiksel kavrama göz atmamız iyi olur. Buna göre aynı değere sahip farklı bayağı kesirler elde edebiliriz. Bunu anlamanın bir yolu konuyu pizza üzerinden somutlaştırmaktan geçer. Bir pizzayı iki kişi arasında yarıya bölerek paylaşabilir ve her birimiz de kendi yarımızı farklı sayıda dilimlere bölebilir ve yine de aynı miktarda pizzayı yiyebiliriz. Benzer biçimde hepimiz daha okul hayatımızın erken dönemlerinde bir yarımın iki çeyrek ve ayrıca üç bölü altı vesaire gibi kesirlerden oluştuğu düşüncesini kavramışızdır:

Bir matematik öğretmeni size, “Kesir çizgisinin üzerinde ne yapıyorsan altında da aynısını yap,” demiştir muhtemelen. Ancak yüksek ihtimalle söylemedikleri şey, bunun denkliği koruduğudur.
Bu, bana bayağı kesirleri ondalıklara çevirmek için bir başka yöntem sunar. Örneğin
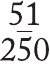
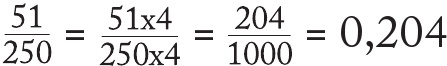
İşlem tamam. Kafa yoracağım bir sonraki şey ise paydayı, onun kuvvetini elde edebilecek şekilde çarpıp çarpamayacağımı nereden anlayacağımdır.
Bunu sınamak için asal sayılar kavramını anlamanız gerekir. Bu sayılar çok uzun bir zamandır matematikçileri büyülemiştir. Kısa ve öz bir şekilde ifade etmek gerekirse bir asal sayı tam olarak iki çarpanı olan bir doğal sayıdır. Örneğin sekiz sayısı sırasıyla bir, iki, dört ve sekizin kendisine bölünebilir ve dolayısıyla dört çarpanı olduğundan asal bir sayı değildir. Beş ise iki çarpana sahiptir, bir ve beş; bu yüzden de bir asal sayıdır. Bir ise tek bir çarpana sahiptir, o da birin kendisidir; bu sebeple de asal sayı değildir. Bu yüzden de “sadece kendisine ve bire bölünen sayı” diye açıklanan saçmalığı unutun gitsin. En baştan başlayarak asal sayıların birkaçını şöyle sıralayabiliriz; 2, 3, 5, 7, 11, 13, 17, 19, 23…
Asal sayıların bu denli müthiş olmasının nedenlerinden biri aritmetiğin asal çarpanlara ayırma olarak adlandırılan kuramıdır. Bu kurama göre her bir doğal sayı asal sayıların çarpımı olarak yazılabilir, ancak sadece bir şekilde. Örneğin:

Asal sayıların 30’u elde etmek üzere çarpımının bundan başka hiçbir birleşimi yoktur. İki, üç ve beş sayıları otuzun asal çarpanlarıdır. Bana göre bu durum asal sayıları matematiksel DNA yapar; her sayı eşsizdir ve sayılar arasında endişelenmemizi gerektiren ikizler ya da klonlar bulunmaz! Hatta 223.092.870 gibi çok büyük bir sayı bile asal sayılar ile sadece bir şekilde yazılabilir (bu da aslında 2 × 3 × 5 × 7 × 11 × 13 × 17 × 19 × 23’e eşittir).
Peki, bu durumun bayağı kesirlerde bana nasıl bir faydası olur? Aslında daha önce bir bayağı kesrin sonlandırılması için paydasını on sayısının bir katına dönüştürebilmem gerektiğinden bahsetmiştim. On sayısının asal çarpanları şöyledir:

Yüz sayısının asal çarpanlarını elde etmek için ise şunu hatırlamak yeterlidir:

Böylece on sayısının asal çarpanları iki ile beş olur ve aynı şey yüz sayısı için de geçerlidir (sadece biraz fazla sayıda iki ve beş gerekir). Buradan on sayısının herhangi bir katının asal çarpanlarının sadece iki ve beş olduğunu anlayabiliriz. Bu yüzden şayet paydamın asal çarpanları herhangi bir şekilde ikiler ya da beşlerin birleşiminden oluşuyorsa o halde bunu on sayısının katını elde edebilecek şekilde çarpmanın da bir yolu vardır demektir. Yukarıda verdiğim bayağı kesir 250 gibi bir paydaya sahipti ve bu da şu şekilde yazılabilir:

Bu birleşim sadece ikiler ve beşlerden oluşmaktadır. Yukarıda bu sayıyı 1000’i elde edecek şekilde 2 × 2 olan dört ile çarpmıştım. Şayet payda 240 olsaydı:
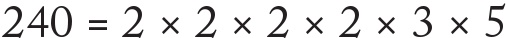
olurdu. Bu sefer çarpım birleşiminde bir tane üç var. Yani en basit haliyle paydası 240 olan herhangi bir bayağı kesir tekrarlanacaktır. Örneğin:

Diğer yandan ise:
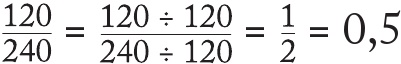
Bu bayağı kesir en basit haliyle artık iki ya da beşten başka bir paydaya sahip olamaz ve bu yüzden de sonlanır.
Bayağı Kesirleri Toplama ve ÇıkarmaHazır bayağı kesirler konusundayken aritmetik hesaplamalarını yeniden özetlemek yerinde olacaktır. Toplama ya da çıkarma yapmak için bayağı kesirleri aynı paydaya sahip olacak şekilde dönüştürmek gerekir. Bunu en etkili biçimde yapmak için de her iki paydanın da çarpanı olduğu en düşük sayıyı aramamız gerekir: en küçük ortak çarpan. Örneğin sekizde beş ile on ikide yediyi toplamak istersem, sekiz ile on ikinin her ikisinin birden çarpanı olduğu en küçük sayıyı belirlemem gerekir. Çarpım tablosundan hemen hem sekiz hem de on ikinin içinde bulunduğu yirmi dördü belirleriz:

Buna payı paydasından büyük olduğu için en ağır ya da bileşik kesir denir. Bu, matematikte lise seviyesine ya da eşdeğerine ulaşana dek kabul edilmez bir durumdur nedense. Bence bunun nedeni her ne kadar bileşik kesirlerle hesaplamalar yapmak daha kolay olsa da ilk bakışta tam sayılı kesirleri anlamanın daha kolay olmasıdır. Bileşik bir kesri karma kesre çevirmek için
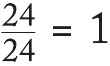
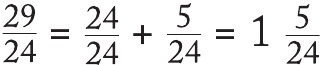
Çıkarma işlemi de benzer biçimde gerçekleştirilir:

En küçük ortak çarpan 36’dır. Denkliği, paydası 36 olan kesirlere dönüştürmek üzere kullanın.
Bayağı Kesirleri Çarpma ve BölmeÇarpma işlemi çok kolaydır; payları ve paydaları birbirleriyle çarparım. Örneğin:
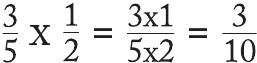
Bir bayağı kesir ile çarpım yaptığınızda toplam değerin küçüldüğünü belirtmekte yarar vardır. Ayrıca burada bir yarım değeri (1/2) bayağı kesirleri bölmede bize yardımcı olacak bir şeyi vurgulamak üzere özellikle seçtim. Yukarıda bir yarım değer ile çarpımın aslında ikiye bölmeye eşdeğer olduğunu görebiliyoruz. Ve benzer biçimde üçte bir değerle çarpım da aslında üçe bölmeye eş olacaktır. Bu ilişkiye bir sayının tersi denir. İki ile yarım (1/2) birbirlerinin tersidir ve şayet iki sayısını bayağı bir kesir olarak yazacak olursam bu durumun nasıl işlediği açıklığa kavuşur:

Herhangi bir sayıya bölmek, onun tersi ile çarpmanın aynısı olmasından dolayı aslında bu oldukça kullanışlıdır.

Bu bilgiyi bayağı kesirleri bölmek için kullanabilirim:
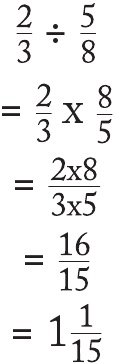
On beşin asal çarpanları üç ile beştir ve bu yüzden
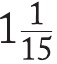
Asal sayıların matematikçiler tarafından bu denli ilgi odağı olmasının nedenlerinden biri de şimdiye dek hiç kimsenin asal sayılar için belirli bir model ya da formülü keşfetmemiş olmasıdır. Birçok kişi denemiş ancak başarıya henüz ulaşamamıştır. Örneğin Fransız rahip Marin Mersenne (1588-1648) şu formülü kullanarak bir dizi sayıyı hesaplamıştır:
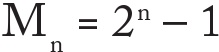
İlk sayıyı belirlemek için n’yi bir olarak alırsınız, ikinci sayı için de n’yi iki olarak alırsınız ve bu şekilde devam eder. Buradan hareketle şöyle bir dizi oluşur:

Mersenne bu formülle elde edilen sayıların bazılarının 3, 7, 31 ve 127 gibi asal sayılar olduklarını fark etmiştir. Bu sayılar da dizideki ikinci, üçüncü, beşinci ve yedinci sayılardır. İki, üç, beş ve yedinin kendisi de ayrıca asal sayılardır. Dolayısıyla görünüşe göre n yerine bir asal sayı koyduğumuzda formülden bir asal sayı elde edersiniz. Ancak yediden sonraki asal sayı on birdir ve formüle göre M11 = 2047 eder. Ne var ki 2047 bir asal sayı değildir çünkü 2047 = 23 x 89 eder.