Bir Nefeste Matematik

7. Bölüm

İKİLİ SİSTEM

İlk bölümde bilgisayarlardan ve kolayca gerçekleştirdikleri aritmetik işlemlerden nasıl faydalanabileceğimizden bahsetmiştim. Bununla nirlikte bilgisayarlar çoğunlukla insan zekâsının ürünüdür. En nihayetinde elektronik bilimden yararlanıp ikili sistemle hesaplama yapabilen makineler meydana getiren, yani bilgisayarları dijitalleştiren de insan zekâsıdır. Bu, her basamak değerinin on sayısının katı olduğu (1, 10, 100, 1000 vs.) bizim kullandığımız ondalık sistemin aksine basamak değerlerinin iki sayısının katları olduğu (1, 2, 4, 8, 16 vs.) bir sayı sistemidir.

Bunun nedeni ise, elektronik bakış açısıyla, elektrik gerilimlerini ya sıfır ya da sıfır-değil (sıfır-değiller bir olarak sayılır) olarak görmenin daha kolay olmasıdır. Şayet sıfır volt değerindeki gerilimler için sıfır, bir volt için bir ve benzeri biçiminde bir analog ondalık sistem kurmaya çalışsaydık bilgisayar içindeki bileşenler arasındaki kablonun uzunluğuna bağlı olarak gerilim değerlerinin düşmesinin yanı sıra bilgisayar ısındıkça içindeki bileşenlerin de direnci değişeceğinden bazı sorunlarla karşılaşırdık.

Modern bilgisayarların hesaplama sisteminden dolayı ikili sistemin oldukça modern bir icat olduğunu düşünebilirsiniz. Ancak öyle değil. Dünyanın çeşitli yerlerindeki farklı kültürler, hemen hemen her türden farklı durumda ikili sistemi kullanmışlardır. Çin’de MÖ sekizinci yüzyıldan beri kehanetleri görmek için kullanılan I Ching (Değişimler Kitabı), ikili yin yang sembollerine dayanan trigram ve heksagram ve sembolleri kullanmaktadır. Büyük Alman matematikçi Gottfried Leibniz (1646-1716), I Ching’e hayran kalmış ve ve 1600’lerin sonlarında modern ikili sistemi tasarlamıştır.

Buradan sonra ise İngiliz mantıkçı George Boole (1815-64), The Laws of Thought (Düşünce Yasaları) isimli kitabında ikili sayıları kullanan bir mantık sistemi düzenlemiştir. Amerikalı matematikçi Claude Shannon (1916-2001) günümüzde Boolean mantığı olarak bilinen bu sistemi ilk kez 1937 yılında elektronik bir devrede kullanan ilk kişi olmuş ve sistemin aritmetik ve mantık işlemlerinde kullanılabileceğini de göstermiştir. Shannon ikili bilgiyi temsil etmek üzere anahtarlar kullanmıştır. Anahtar kapalı iken sıfırı, açık konumdaykense biri temsil etmektedir.

Shannon, İkinci Dünya Savaşı sırasında Nazi şifrelerini kırmada bilgisayarların kullanımı üzerine tartışmak için İngiliz matematik kahramanı Alan Turing (1912-1954) ile buluşmuştur. Çalışmalarının aslında birbirlerinin çalışmalarını tamamladığını keşfetmişlerdir. Shannon’un 1948 tarihli, “İletişimin Matematiksel Kuramı” başlıklı makalesi onu bilfiil tüm modern dijital bilgisayarların babası kılmıştır.

Şayet bir bilgisayar gibi aritmetik işlem gerçekleştirmek isterseniz ikili sistemde 1 + 1 = 10 olduğunu unutmadığınız takdirde kuralların aynı kaldığını görmekten memnun olacaksınız. Örneğin 101 + 110 işlemi şu şekilde görünecektir:

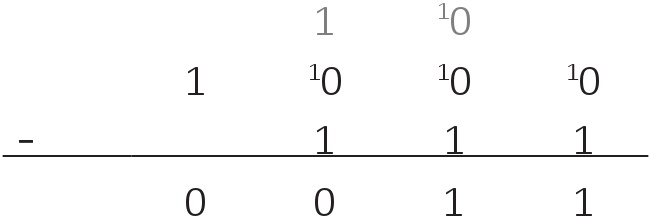
Şayet 10 – 1 = 1 olduğunu hatırlayacak olursak 1010 – 111 ise şöyle görünecektir:

101 x110 ise şöyle görünecektir (aslında ondalık çarpım tablosuna dair bütün o bilgiye ihtiyaç duymadığınızı dikkate alın!):

Buradan da 10100 + 1010 = 11110 olur.

Bölme işlemi için ise 1010 ÷ 100 şu şekilde hesaplanır:

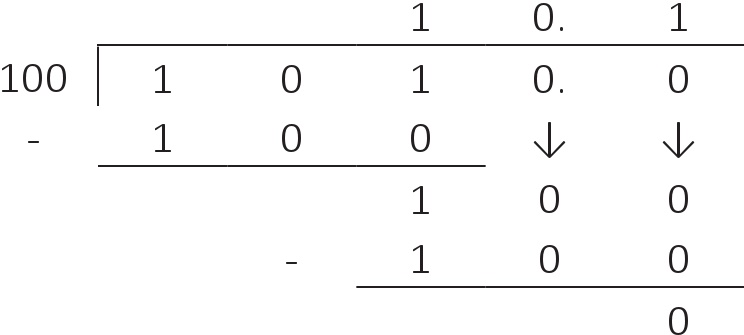
İkili sistemde de bayağı kesirlerimiz olabildiğine ve ondalık virgülün sağındaki basamakların yarım, çeyrek, sekizde birler vs. şeklinde olacağına dikkat ediniz. Bu yüzden burada 0,1 yarım değeri temsil etmektedir.

Buradaki tüm hesaplamaları kontrol etmek üzere ondalık sayıya çevirmeyi okuyucular için bir alıştırma olarak bırakıyorum!

Bir bilgisayarın hesaplamaları ne kadar hızlı gerçekleştireceği konusundaki sınırlayıcı faktör, bir mikroçipin içine sığdırılabilecek anahtarların (ya da transistörlerin) sayısı ve ayrıca bunların ürettikleri ısının üstesinden gelebilmesidir. Şimdilik yedi milyar transistörü piyasada satılan küçük boyutlardaki bir bilgisayar yongasına sığdırmak mümkündür. İntel şirketinin kurucularından Amerikalı girişimci Gordon Moore, 1965 yılında mikroçiplerin teknolojik olarak gelişiminin üzerlerindeki transistör sayısının her iki yılda bir iki katına çıkmasına izin vereceğini belirtmiştir. Bu süreç Moore yasası olarak bilinir.

Moore yasası, yapabileceklerimizin fiziksel sınırına yaklaşırken son beş yılda hız kesmiştir. Günümüzde üretilen transistörlerin boyutu sadece nanometrelerle ölçülür. Bu da milyonlarcasını bu cümlenin sonundaki noktaya sığdırabileceğiniz anlamına gelir. Pekâlâ, buradan nereye gidiyoruz?

Olasılıklardan birisi, teorik olarak geleneksel dijital bilgisayarlardan çok daha hızlı çalışmalarını sağlayacak kuantum mekaniğinin tuhaf etkilerine dayanan kuantum

Конец ознакомительного фрагмента.

Текст предоставлен ООО «Литрес».

Прочитайте эту книгу целиком, купив полную легальную версию на Литрес.

Безопасно оплатить книгу можно банковской картой Visa, MasterCard, Maestro, со счета мобильного телефона, с платежного терминала, в салоне МТС или Связной, через PayPal, WebMoney, Яндекс.Деньги, QIWI Кошелек, бонусными картами или другим удобным Вам способом.

1

Gerçek bir sıcak hava balonunun yükselmeye devam edeceğinin tamamıyla farkındayım. Bu yüzden de bu balonun fiziksel değil matematiksel bir balon olduğunu belirttim.