The Genius in my Basement

*6 The Monster

(Mathematical chapters in this book are quarantined by a *)

That’s the name of Simon’s special area in mathematics, because of its gargantuan complexity and fiery insight into the fundamental structure of our universe.

No one knows what the Monster looks like. It can be detected only through its mathematical traces. Like shadows and ghosts, it inhabits a penumbral landscape between abstraction and solidity.

The Monster belongs to an area of mathematics known as Group Theory, or the study of symmetry.

Groups are represented in textbooks by tiresome grids of numbers similar to sudoku tables, yet they are among the most startling investigative tools in human thought. Quantum Theory, Relativity Theory, predictions about the number and types of sub-atomic particles, the codes used to scramble military and financial information – all of it fundamentally reliant on the study of Groups. They have even been used to investigate incest among Aboriginal tribes.

A sudoku table has nine rows and nine columns of numbers.

The Monster has 8080174247945128758864599049617107 57005754368000000000.

*7

Introducing

To understand Simon’s particular genius – how it developed and why for a few years he led the braying pack of mathematicians hunting down the Monster – the reader needs to know about squares.

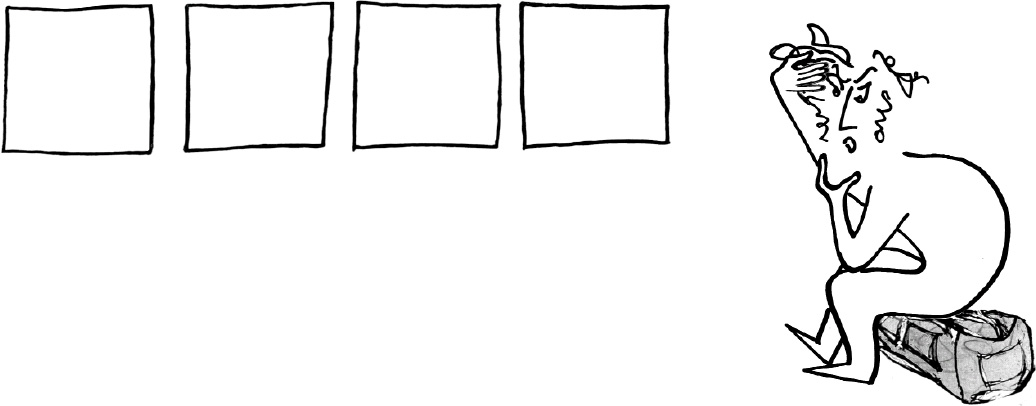
On the face of it, the study of symmetries is a subject for children. A square has symmetry: you can rotate it, and the result looks just as if you’d done nothing at all:

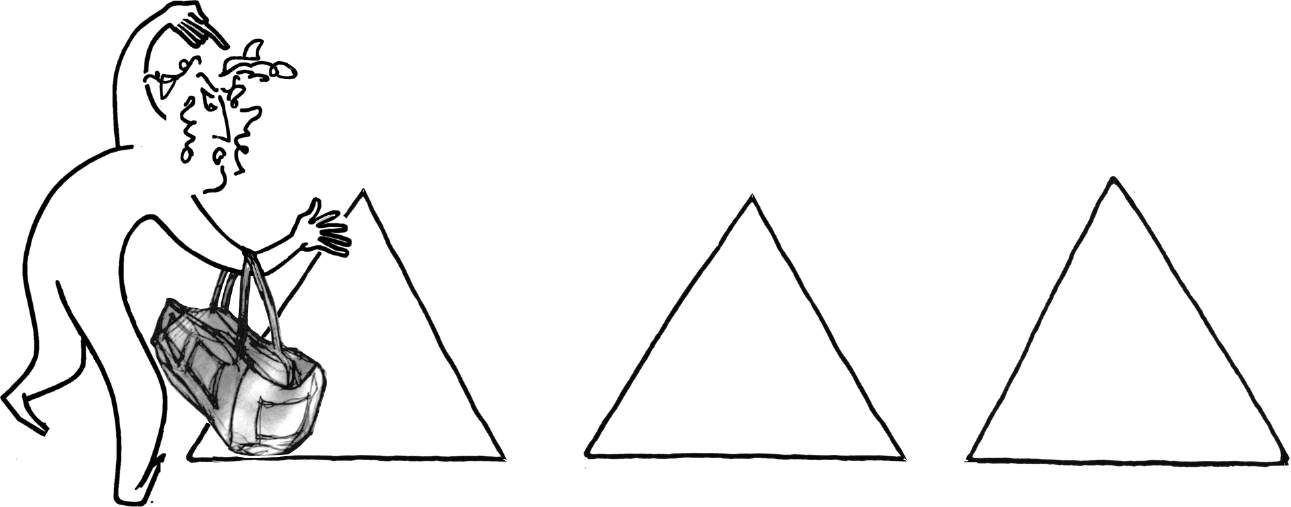
The same goes for an equal-sided triangle:

A circle, cube, sphere, and a host of other shapes with names like dodecadodecahedron (twenty-four faces) and icosidodecadodecahedron (forty-four faces) each has similar symmetrical properties.

In order to develop mathematics out of such simple stuff, we have to keep a diary of these symmetries.

For example, to keep track of these four moves, we can represent them like this:

Note that there’s a sense of self-containment about this set of operations. A square has four sides and therefore only four distinct ways of rotating. After that, you’ve exhausted all the possibilities. No amount of rotating will paint it green or puff it up to twice its original size. Other operations are needed to perform that sort of thing.

If we rotate a square in any of the above four ways, it still looks to the outsider just like the square we started with:

But, privately, we know we’ve been fiddling. For example, if we rotate a square through two turns (i.e. flip it head over heels), we can represent this:

In other words,

signifies the act of swivelling a square through two 90-degree turns, without anybody noticing.

Naturally, if you turn a square by one turn through 90 degrees, then do it again, that’s the equivalent of two 90-degree turns overall:

1 + 1 = 2

Similarly, rotate a square once, followed by two more turns, and the result is equivalent to three turns. You’ve almost gone the whole way round:

1 + 2 = 3

And so on. Rotate a square by two turns, then do nothing, go off and play with somebody else’s crayons, and no one’s going to be fooled – it’s still just two turns:

2 + 0 = 2

A square looks just the same after any combination of these operations, or all of them:

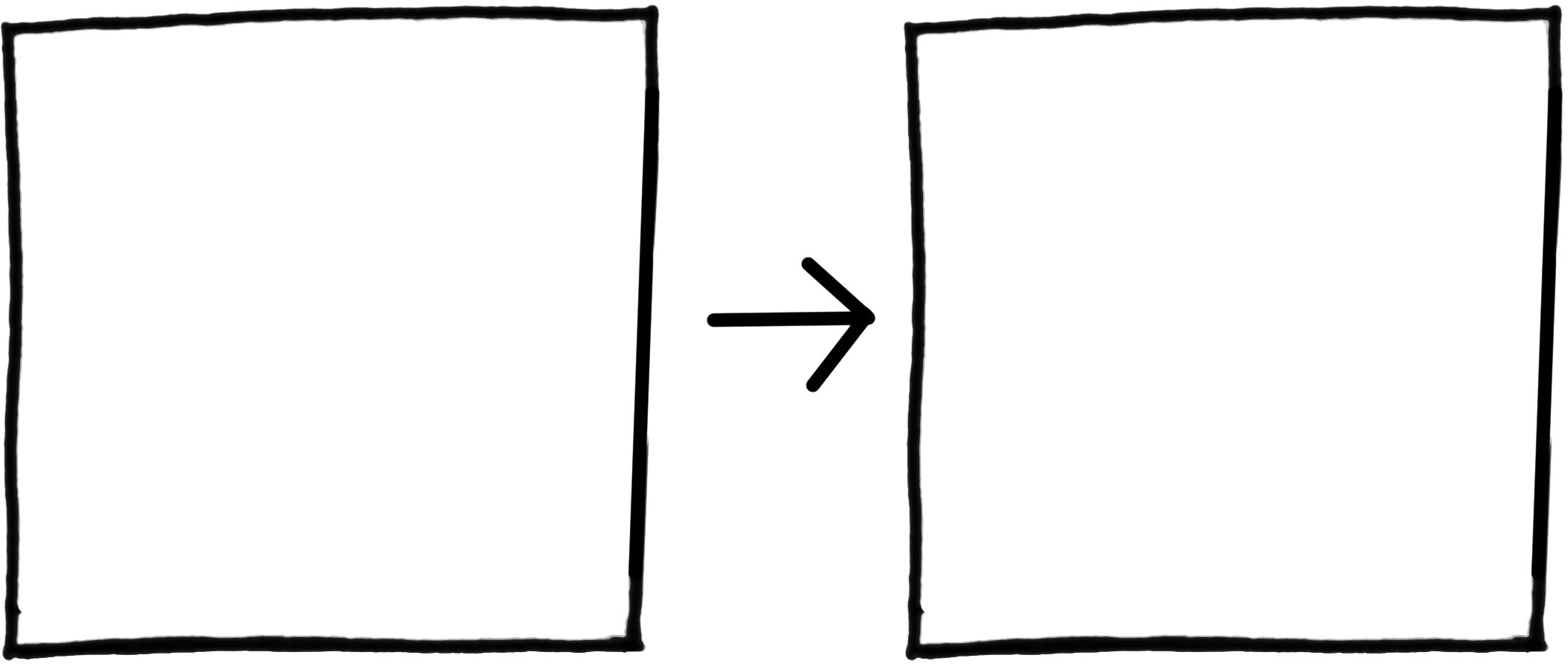
The figures with arms and legs are simply diary entries to keep track of the secret things we’ve been doing to the square in the playpen.

What happens if we turn a square, say, five times? That’s the equivalent of spinning it through a full cycle, then throwing in an extra single turn for good measure:

Group Theory isn’t interested in recording such clever-clogs stuff. Turn a square round five times and you might as well just have turned it once. It’s the final outcome only that matters, so it’s put down as an ordinary single turn:

So, although it seems possible that:

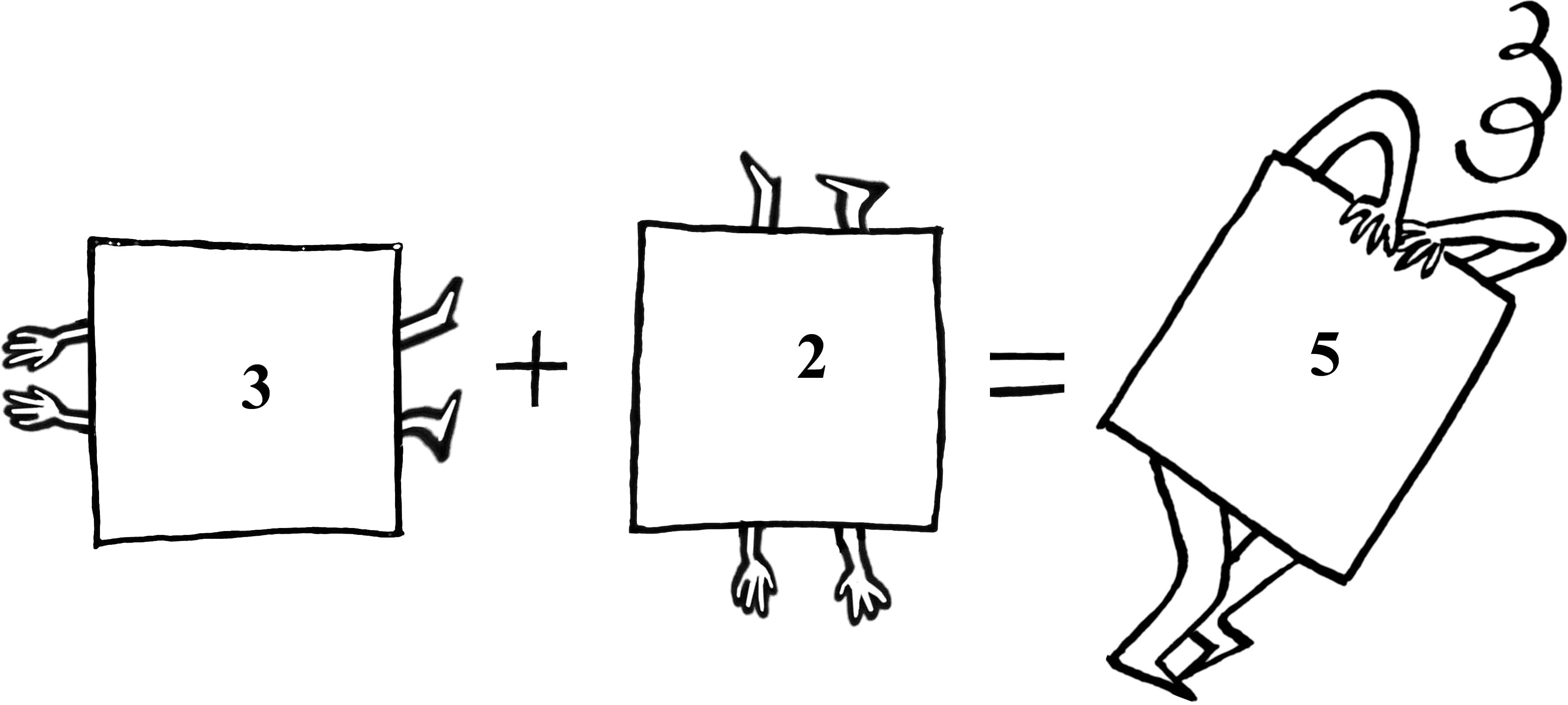
3 + 2 = 5

because the first four turns make a complete rotation, head over heels, back exactly to where we started, we ignore them as wasted effort, and just focus on the one left-over turn, which got us somewhere:

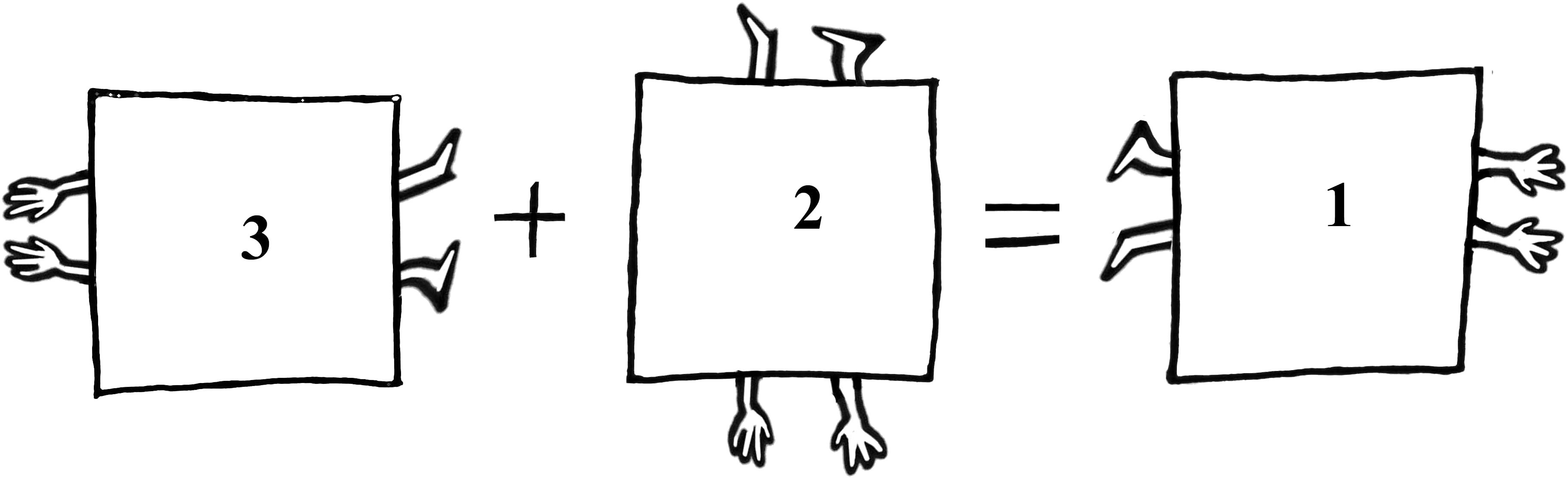
3 + 2 = 1

In this respect, rotating a square is the same as rotating the hour hand on an ordinary clockface. If it’s two o’clock and we add twelve hours, we don’t say it’s fourteen o’clock (unless we’re being tiresome). We say it’s two o’clock again.

All these combinations of turns can now be written down as a chart. These tables are the lifeblood of Group Theory. Every mystery of this secretive, sly subject is contained in them. The one that applies to turns of a square is:

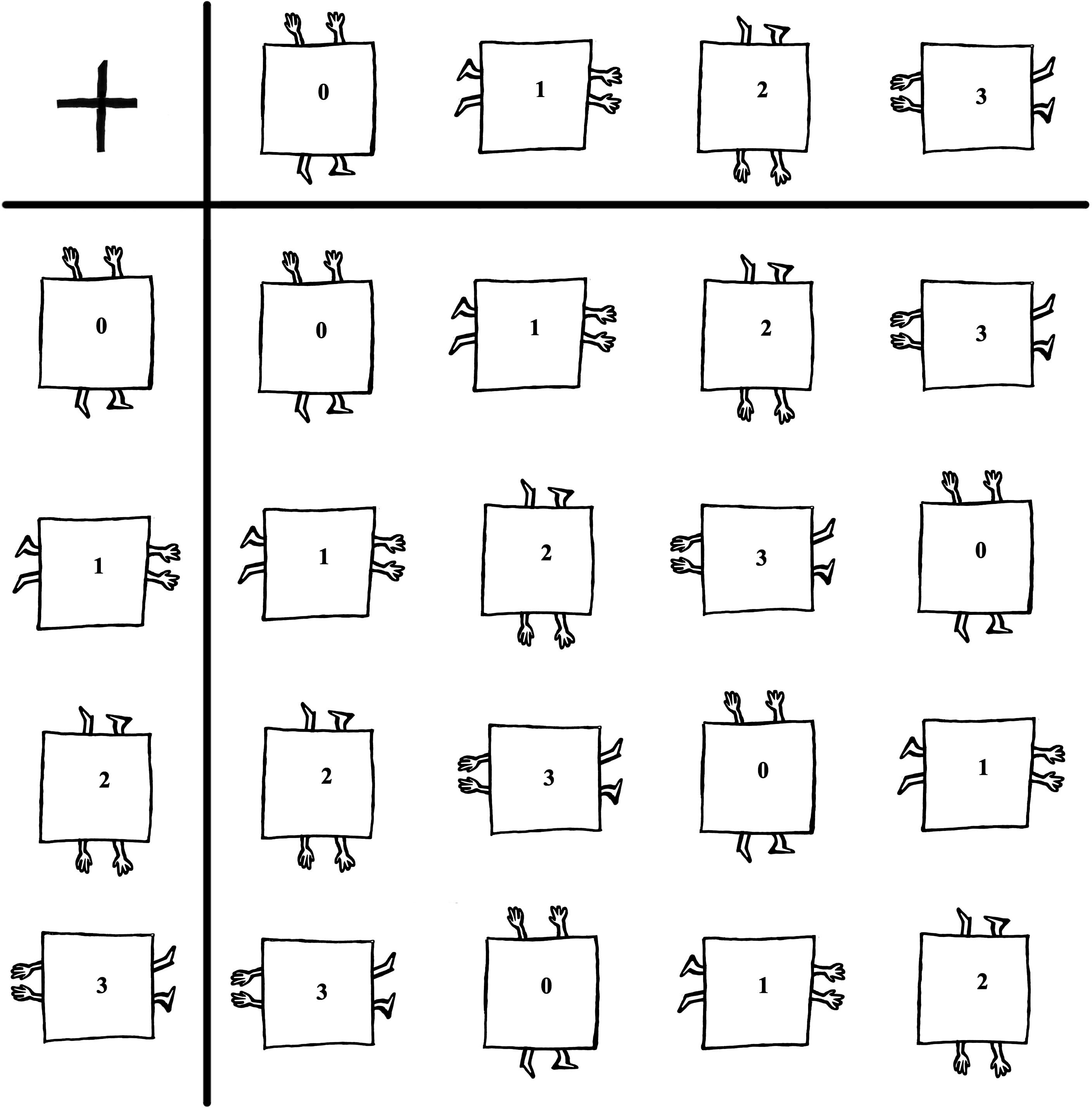
It’s read in the same way as the distance chart at the front of a road atlas. It’s not a calculating device; it’s a secretarial way of keeping track of information. If you’re six years old and want to remind yourself what happens when you turn a square once, then turn it again, i.e.:

take the row corresponding to 1, run your chocolatey finger along until you come to the column corresponding to 1, and there’s the answer – it’s equivalent to two turns:

What’s baffling is that there can be anything complicated enough about this ‘study’ of symmetries to bring it out of the playroom in the first place.

45

The papers that slosh about in the basement are (Simon insists I am to say) ‘carefully, hnnnh, arranged and, uuuh, being sorted in plastic bags’.

But I’ve put my foot down over this: ‘That’s a lie, Simon. You’re telling me to make things up.’

‘I’ve not noticed your reluctance on that front before.’

Simon was taught mathematics by the number 45.

The first written evidence we have of 45’s significance in his life comes from an Atlantic blue notebook dated January 1956 (a year before Simon started school) and entitled

Inside, Simon addresses mathematical problems to this number:

(sums for 45, you 45)

performs amusing numerical games:

and emerges briefly, porpoise-like, from his researches to write letters to her:

Translation: My darling 45 I cried when you went out I had tea and played with you before you go 45 and 47 29 say 1 2 3 82 4 5 6 7 8 9 0 111

before re-submerging in a glug of numbers.

Sometimes, 45 wrote back:

45 was Simon’s number for his mother. She was the one who taught him maths, up to quadratic equations. Astounding, for a British housewife in the 1950s – no one in the family can explain it.

Once the first Atlantic blue notebook was finished, Simon and his mother started another, in February 1956, just before his fourth birthday. Her handwriting is on the cover this time, and she calls him a monkey:

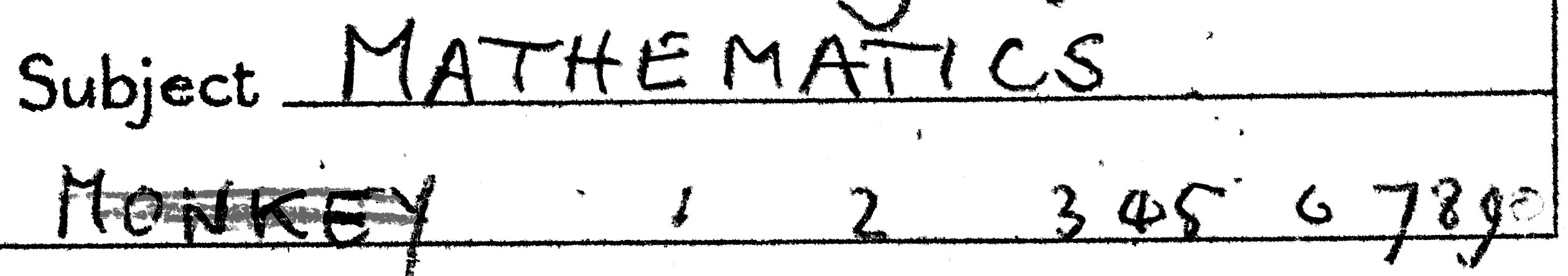
I wonder who crossed this fondness out.

Once, during these pre-school years, Simon was distracted by a word:

But he soon snapped back to numbers with gusto:

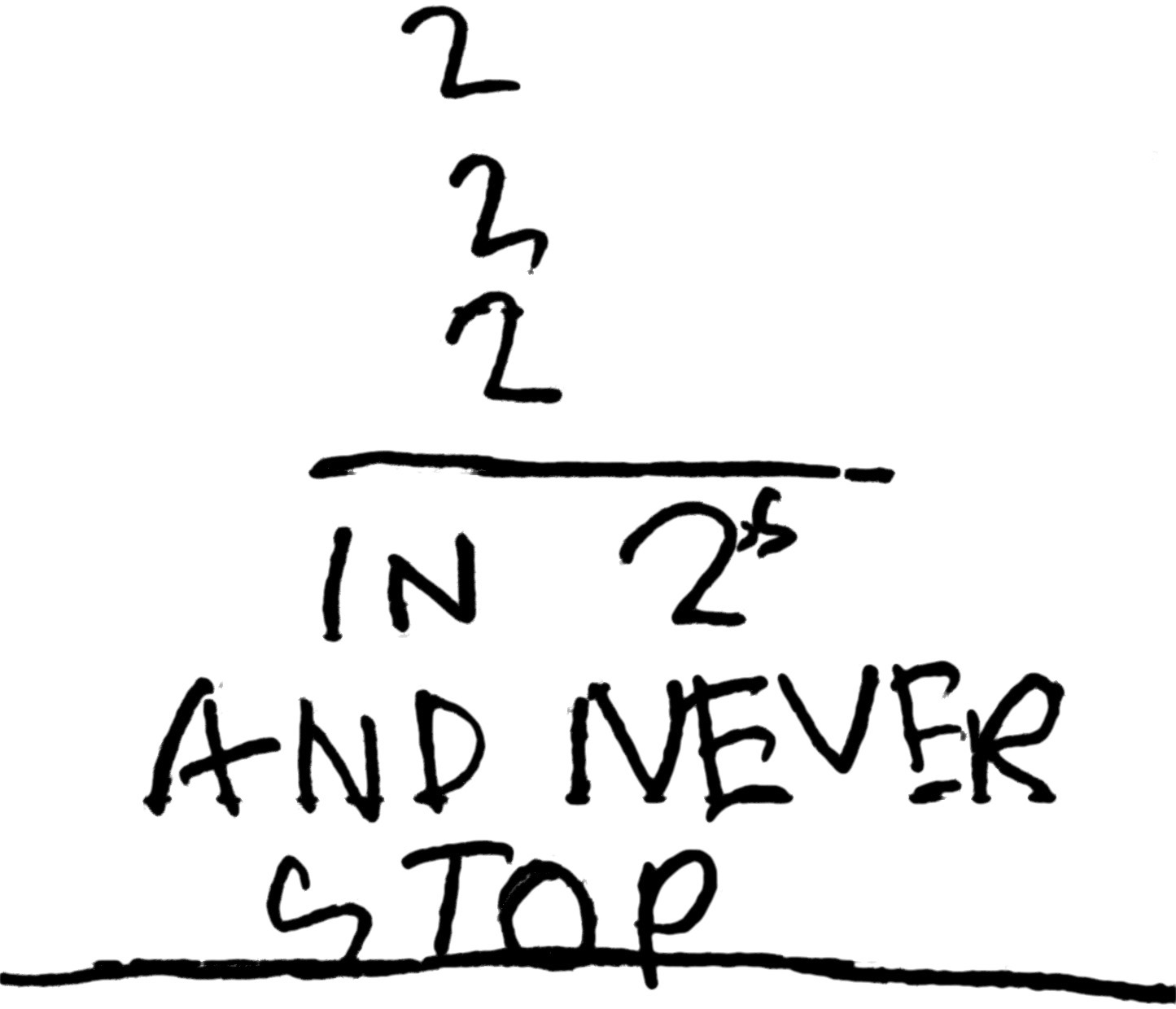
9 eSimon

Simon has five types of grunt:

Ask him about his mother,

his father,

or his parents’ marriage,

and you get a happy grunt for the first, a puzzled one for the second, and an incomprehensible bleat concerning the photo above.

It’s possible to extract more interpretation, if you work at it.

‘Simon, what do you mean, “Uuugheugh … gghuaha … ehhghH”?’

‘Haaaghuggh … oooh … ghughghEH.’

‘These are your parents. You grew up with them. Is this photo an accurate reflection of their relationship or not?’

‘Aaaghurghh … gghahuugh … eeehghuGH … is that a dog in the middle? Oh, it’s a bag. If it had been a dog these might not have been my parents, just people who looked like my parents, because we didn’t have a dog.’

‘Don’t you think there’s something remarkable about this picture? Sitting back to back on a pebble beach in Southern England with something that looks like a dead bulldog between you?’

Simon looks trapped and panicky.

‘Or is this just a snapshot of what marriage always is, to you?’

The grunt-bleat means bafflement. Why should he find something odd about the photograph? It’s a photograph: one of those things (so rare in life) in which a fact is made immutable. Why muddy it with interpretation? Why, if you do muddy it, pick on that particular interpretation? It could be one of a million others.

Simon is, verbally, one of the most adept and playful people I know – as long as he doesn’t have to speak.

Or use metaphor.

Or comment on photographs.

Simon’s parents’ marriage (according to other members of the family) was not happy or unhappy, just mannered and soulless.

The puzzled father-grunt Simon gives about his father signifies a lack of interest. The happy mother-grunt, ‘loveliness’. Loveliness is the only adjective Simon associates with Helene Norton. She ‘embodied’ the word, he says. There isn’t need for others – and he doesn’t mean ‘loveliness’ because of her startling beauty, which Simon claims he’d never noticed until I started ogling her, but ‘loveliness’ because of … because of … uuuggghhhAH! Grunt Number Four: Frustrated Grunt.

What’s the point of me demanding new words when he’s already given me the one that works to perfection?

‘Loveliness’ does not mean uncensoriousness, however. When his mother was alive, Simon used to visit her in London every two or three weeks, but she refused to greet him until he’d had a bath.

Then she would criticise his clothes.

‘If it wasn’t one thing, it was another,’ remembers Simon forlornly. ‘I got the feeling I could never satisfy her. Did it count if your clothes were wrong in the period before you’d had a chance to spruce up between the front door and the bath?’

After trying to ‘spruce up’ he’d step out of the bathroom in the fresh clothes that his mother kept in a cupboard, ready for his visits, and expecting now to be allowed to kiss her hello. ‘But I’d almost certainly forget something, and she’d draw attention to that one thing and home in on it. My shirt was wrong, or my shoelaces were undone. I hadn’t done up my trousers correctly.’

He gives a purgatorial groan.

‘It was too much for me.’

Two or three days after his mother’s death (Simon remembers it as ‘rather too quickly’) he and his two brothers let themselves into her five-bedroom apartment near Baker Street, and began picking over her possessions. From their mother’s cupboards and drawers they extracted everything small and unbreakable and piled it on the floor. Then they shuffled among the piles – in my image of this spectral, sacrificial scene I imagine them as three tall birds, and hear the clicking of their feet on the parquet floors – plucking up anything that took their fancy.

There was only one item Simon wanted: a photograph of his mother in old age.

There were paintings of her, when she was young and glorious. Simon wasn’t interested. He’d had nothing to do with her in those days. He doesn’t like portraits at the best of times, but he prefers at least that they correlate to an image already in his brain.

He held out his arms, eyes closed, to any other things the brothers didn’t take , then brought the fifty-or-sixty-item windfall back to a small flat he owns in London. There he laid them out, ten layers deep along one edge of the living room, like drying fish fillets.

Simon tells me he would like to hang the pictures up.

His mother has been dead nine years now, but the haul remains stacked against the wall, curing itself slowly of connotations. ‘Loveliness’ now resides only in the photograph of her old age and his memories.

The leftovers in his mother’s apartment – her letters, wrapped in pink ribbon, from a man who was not Simon’s father; her skirts and chemises, brooches, diamond pins, fur coats, perfumes, old swing-band records – the brothers sold, gave away or threw in the dustbin.

‘But you also got all your old school reports and exercise books, and the folder of newspaper clippings about when you won the Maths Olympiads and went to Cambridge, your IQ report?’

‘As I say, I didn’t want them.’

‘Then why take them?’

‘Why not take them?’

Simon is always eager to drop in schoolboyish retorts like this. The trick is to become instantly absurd.

‘Would you have taken them had they been roast chickens?’

‘Heh, heh, heh, hnnn. I took them because it’s the sort of thing people do take, isn’t it?’

See? Simple, when you know how.

To Simon, correct conduct is like a wood. It has many trees, which represent how things ought to be done; one tree for each circumstance. It is a large wood, sterile and rather dark. The stormy forest where he goes to hunt for the Monster is infinitely more comforting.

Here’s Simon’s brother!

Hello, Michael!

He doesn’t have much to say.

‘Is it surprising?’ he protests, leaping up, holding out his hand – a strong shake. ‘I’m ten years older than Simon is. We were like different families. I studied chemistry at university, not mathematics; that’s a different language. Simon is interested in chemistry also? Really? I never knew. His favourite element is Boron? I’m surprised! Would you like some tea? Organic Lapsang or elderflower?’

Michael Norton OBE is the author of Writing Better Fundraising Applications, The WorldWide Fundraiser’s Handbook, The Complete Fundraising Handbook and Getting Started in Fundraising. Money – in particular other people’s money – is a big subject in Michael’s life. He wants it to pay for environmental revolution.

His latest book is 365 Ways to Change the World: How to Make a Better World Every Day. Each day of the year is allocated a noble deed:

5 January: ‘Start drinking.’ Reduce ‘beer miles’ by giving up sewage brands like Heineken or Budweiser, and brew your own beer using oysters and wild rice.

22 February: ‘Say no to plastic bags.’ There are now 46,000 pieces of plastic waste in every square mile of the world’s oceans. In Australia, eighty million plastic bags are added every year to the mist of garbage that floats across the scrub there. Cows eat them and die; then the sack re-emerges from the rotting flesh, is cleaned off by rain, scooped back up by wind, and bundled along to be eaten by another cow: it is, biologically speaking, a protovirus. Simon is therefore a force for salvation. He keeps these viruses out of reach. If it weren’t for him, thousands of extra plastic bags from the Excavation would be tumbling through our fields and woodlands.

1 May: ‘Join the sex workers’ union.’ Fight to give prostitutes access to health care, safe places to work and legal support against rapists and pervy Italian prime ministers. ‘Membership is free.’

‘Michael Norton is a one-man “ideas factory”,’ bellows the Guardian.

‘You know, he knows when he comes to dinner here dressed in a dirty T-shirt that he’s doing wrong,’ says Michael, stooping under the lintel of his cottage door (he lives in Hampstead, but the house looks as if it’s been airlifted from beside a village brook in Hampshire) and balancing a tea tray. ‘But there’s no point telling him. You’d physically have to burn his old clothes before he’d get rid of them.’

He’s brought a photograph album into the garden along with the Victoria sponge cake. The album’s green, with a cushioned cover, from 1954, and it’s all the paperwork Michael has that includes Simon. They are not a sentimental family.

‘That’s my hand at the edge there, sorting out his food, even at that age. We’re at our summer bungalow in Ferring. This is David …’. David is a friend who later murdered his wife by bludgeoning her to death with a champagne bottle:

‘And here’s Simon aged … oh dear, not a pleasant-looking young man’:

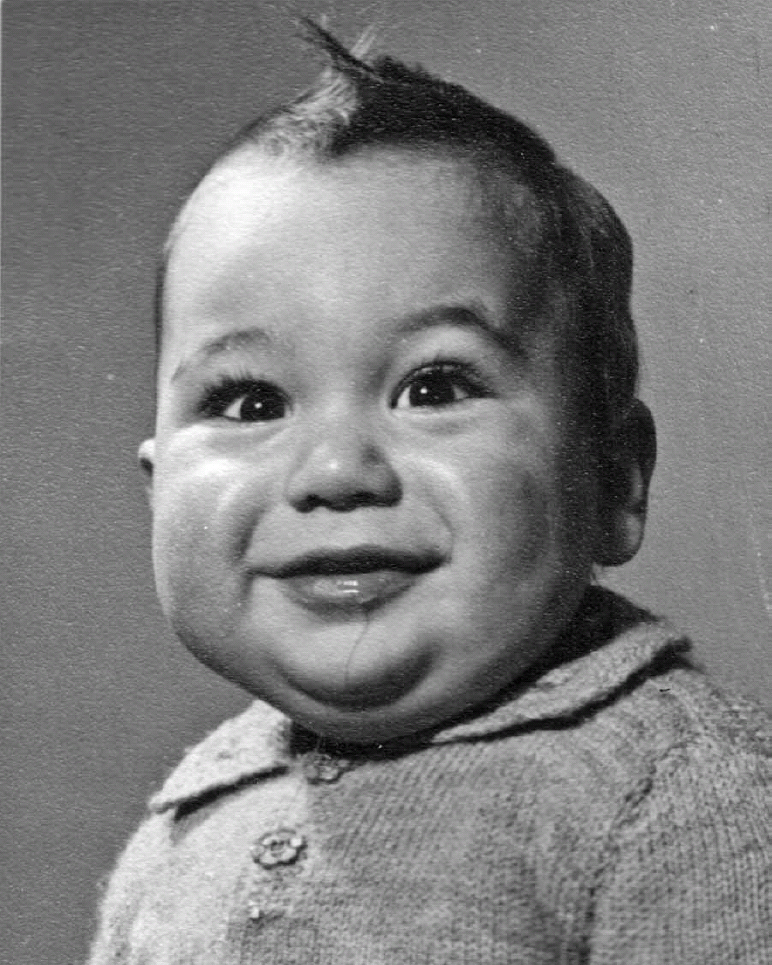
‘Our mother doted on Simon. She was really proud that he was a genius. I don’t think she ever understood why he didn’t sustain that. I mean, he sustained it in his brain, but why is he not a professor? Why has he not got a proper job?’

‘He’s too peculiar,’ I suggest.

‘He’s not that peculiar,’ retorts Michael sharply, catching me out, correctly, in one of the phrases I have lately come to use about Simon without thinking. ‘There are lots of peculiar people in Cambridge. Half the dons that I had as a student there were peculiar. There must be somewhere that would give him a home.’