Энциклопедия финансового риск-менеджмента

1.23. Расчет волатильности финансовых показателей на основе исторических данных

Волатильность, или изменчивость (volatility), финансовых показателей играет очень важную роль в управлении финансовыми рисками.

Пусть Yt – некоторый финансовый показатель (например, цена или доходность некоторого финансового инструмента), наблюдаемый в день t, t = 0, 1, 2, …, T. Положим

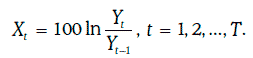
Случайная величина Xt представляет собой натуральный логарифм относительного изменения этого показателя за один день, выраженный в процентах. Тогда дневную волатильность данного показателя можно оценить следующим образом:

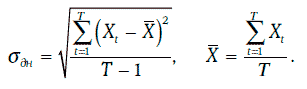
Иными словами, дневная волатильность принимается равной стандартному отклонению логарифма относительного изменения финансового показателя за один день.

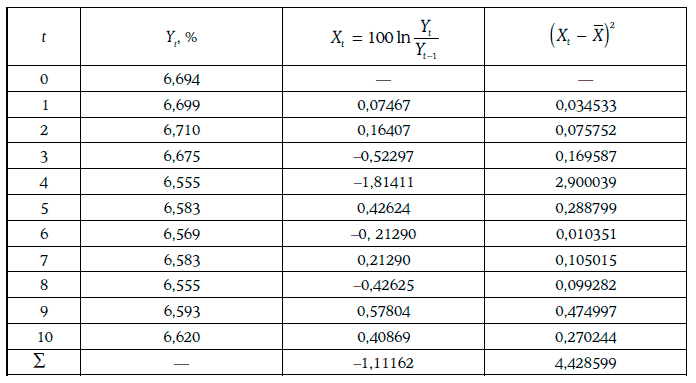
Пример 1.60. В течение 11 последовательных рабочих дней биржи определялась доходность 30-летних казначейских облигаций с нулевыми купонами. Расчет дневной волатильности доходности на основе этой информации приведен ниже.

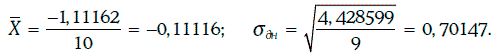
Таким образом, дневная волатильность доходности 30-летних облигаций с нулевыми купонами оценивается в 0,70 %.

Если случайные величины Xt не коррелируют между собой, то, зная дневную волатильность доходности финансового инструмента, можно оценить волатильность доходности этого инструмента за данный период времени:

В частности, для того чтобы определить годовую волатильность, необходимо для каждого конкретного случая правильно определить число рабочих дней в году. Число рабочих дней в году может быть равным 250, 260 или 365.

Пример 1.61. В примере 1.60 была найдена дневная волатильность доходности 30-летних казначейских облигаций с нулевыми купонами: σдн = 0,70147.

Ниже указана годовая волатильность доходности при разных оценках числа дней в году:

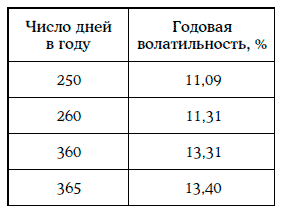
Предположим, что в данный момент времени доходность финансового инструмента равна r. Можно считать, что доходности за один день распределены логнормально с параметрами 0 и σдн. Если логарифмы относительных изменений доходности не коррелируют между собой, то отношение доходности через год к доходности г будет распределено также логнормально, но с параметрами (0, σгод). Следовательно, сама доходность финансового инструмента через год должна иметь логнормальное распределение с параметрами (ln r, σгод).

Если годовая волатильность доходности достаточно мала, то можно считать, что доходность финансового инструмента через год распределена приблизительно нормально с параметрами r и rσгод.

Пример 1.62. Текущая доходность 10-летних казначейских облигаций с нулевым купоном равна 8 %, а годовая волатильность этой доходности равна 15 %.

Можно предположить, что доходность 10-летних облигаций с нулевыми купонами через год будет приблизительно распределена нормально с ожидаемым значением 0,08 и стандартным отклонением 0,08-0,15 = 0,012. Отсюда, в частности, следует, что с вероятностью 95,5 % доходность через год окажется между 0,08-2 • 0,012 = 0,056 и 0,08 + 2 • 0,012 = 0,104, т. е. будет принимать значение между 5,60 и 10,40 %.

1.24. Элементы регрессионного анализа

Во многих случаях требуется установить зависимость между двумя случайными величинами. Чаще всего предполагается линейная зависимость. Например, при обмене облигаций использовалась линейная зависимость между изменениями доходностей двух облигаций.

Рассмотрим две случайные величины ξ и η и предположим, что когда случайная величина ξ принимает значения X1, X2…., Xn, то случайная величина η принимает соответственно значения Y1, Y2…., Yn.

Линейной регрессионной моделью называют уравнение следующего вида:

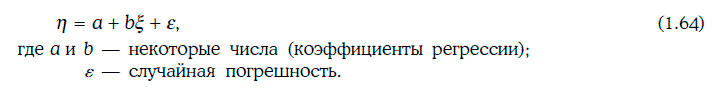
При построении линейной регрессионной модели коэффициенты а и b необходимо подобрать так, чтобы влияние случайной погрешности ξ на случайную величину η было как можно меньше.

Из уравнения (1.64) следует, в частности, что

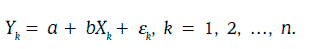
Коэффициенты регрессии а и b чаще всего подбираются методом наименьших квадратов (least squares), который сводится к отысканию значений а и b так, чтобы достигалось наименьшее значение функции

Нетрудно проверить, что наименьшее значение функции (1.65) достигается при

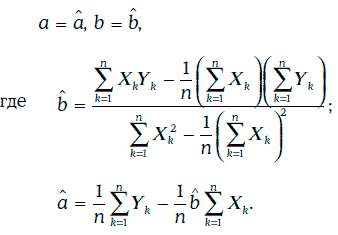
При выборе коэффициентов регрессии указанным выше способом будут выполняться следующие соотношения:

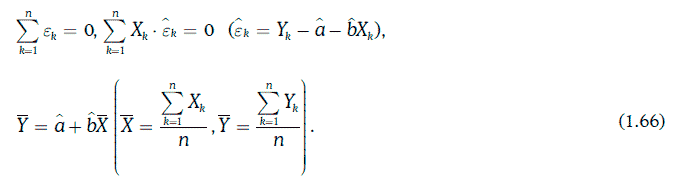
Пример 1.63. Построение линейной регрессионной зависимости доходности среднесрочных корпоративных облигаций одного и того же кредитного рейтинга (η) от доходности 10-летних казначейских облигаций (ξ). Исходная информация и предварительные расчеты приведены в таблице ниже.

Коэффициенты регрессии находят следующим образом:

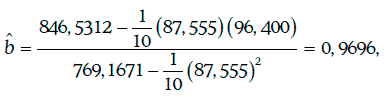
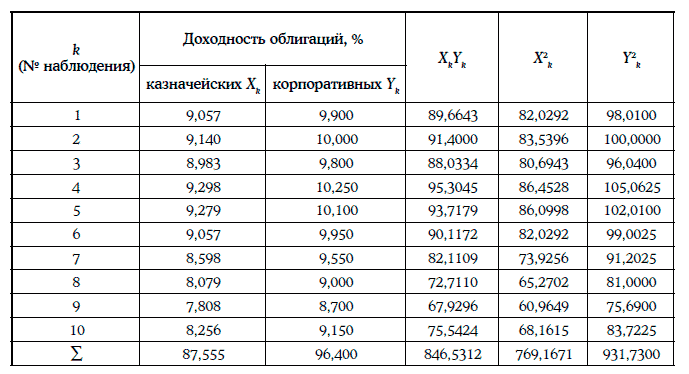
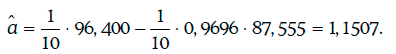
Уравнение регрессии в данном случае имеет вид:

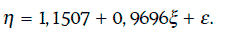
Из соотношения (1.66) следует, что

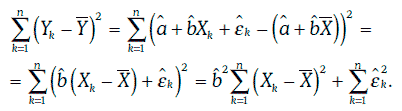
Отношение суммы квадратов, объясняемой регрессией, к полной сумме квадратов называют коэффициентом детерминации и обозначают R2. Таким образом,

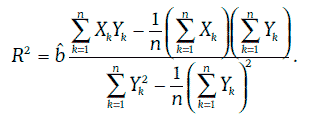
Коэффициент детерминации всегда находится между 0 и 1, причем чем ближе коэффициент детерминации к единице, тем выше качество регрессионной модели.

Пример 1.64. Оценим качество регрессионной модели, построенной в примере 1.63.

В данном случае коэффициент детерминации может быть найден следующим образом:

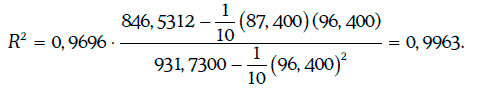
Так как коэффициент детерминации очень близок к единице, то качество регрессионной модели достаточно высокое.

Оценка коэффициентов регрессии получена нами в зависимости от выборки значений X1, X2…., Xn независимой случайной величины ξ и соответствующих им значений зависимой случайной величины η. Для другой выборки значений случайной величины ξ будут получены, вообще говоря, другие оценки коэффициентов регрессии и другая случайная погрешность. В связи с этим возникает задача построения доверительных интервалов для коэффициентов регрессии.

Если предположить, что случайные погрешности не коррелируют между собой (т. е. отсутствует автокорреляция), то доверительные интервалы для коэффициентов регрессии с надежностью 95 % строятся следующим образом:

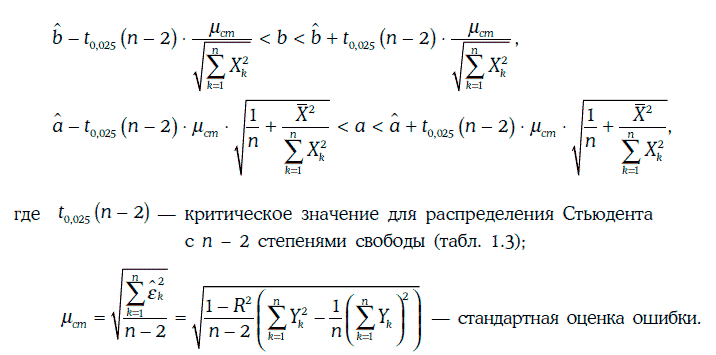
Если случайная величина ξ принимает значение Х, то согласно линейной регрессионной модели:

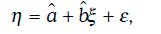
а ожидаемое значение случайной величины η равно

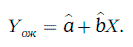
При отсутствии автокорреляции[17] и гетероскедастичности[18] доверительный интервал для значения случайной величины η при заданном уровне надежности может быть найден в виде:

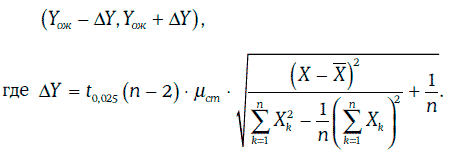
Пример 1.65. Инвестор считает, что через месяц доходность 10-летних казначейских облигаций окажется равной 8 %. Тогда согласно регрессионной модели, построенной в примере 1.63, ожидаемое значение доходности корпоративных облигаций будет равно

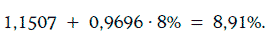
Для определения доверительного интервала для доходности корпоративных облигаций с надежностью 95 % найдем:

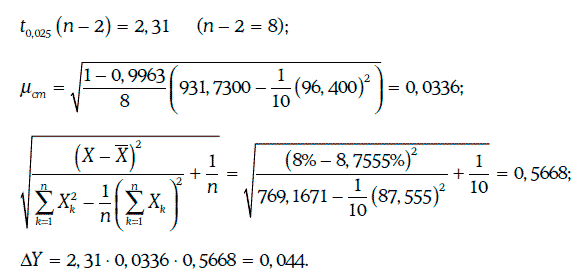
Следовательно, искомый доверительный интервал: (8,87 %; 8,95 %).

1.25. Метод Монте-Карло

Случайная величина γ, принимающая 10 значений: 0, 1, 2, 3, …, 9 с одинаковой вероятностью, называется случайной цифрой.

Предположим, что мы произвели N независимых опытов, в результате которых получили N случайных цифр. Записав эти цифры (в порядке их появления) в таблицу, получим то, что называется таблицей случайных цифр. Например, таблица из 150 случайных цифр может иметь следующий вид (цифры разбиты на группы для удобства чтения таблицы):

Случайным числом (random number) называется случайная величина

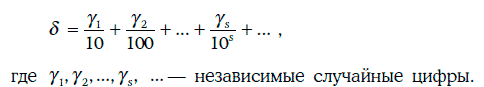
Иными словами, случайное число – это случайная величина, равномерно распределенная на промежутке [0, 1).

Если задана таблица случайных цифр, то можно строить различные случайные числа, как, например:

В настоящее время существуют специальные компьютерные программы для построения случайных чисел в любом количестве. Такие программы называют генераторами случайных чисел.

Рассмотрим теперь дискретную случайную величину ξ, распределение которой имеет вид:

Равенство (1.68) позволяет каждому случайному числу приписать определенное значение случайной величине ξ. Такой процесс приписывания значений случайной величине ξ часто называют разыгрыванием этой случайной величины.

Пример 1.66. Случайная величина ξ принимает значения 1 и 2 с вероятностью 0,6 и 0,4 соответственно. В данном случае

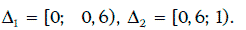
Значения этой случайной величины, приписываемые случайным числом из последовательности (1.67), приведены ниже:

Частоты появления 1 и 2 соответственно равны

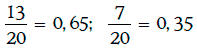
Предположим, что даны две случайные величины ξ и η, совместное распределение которых имеет вид:

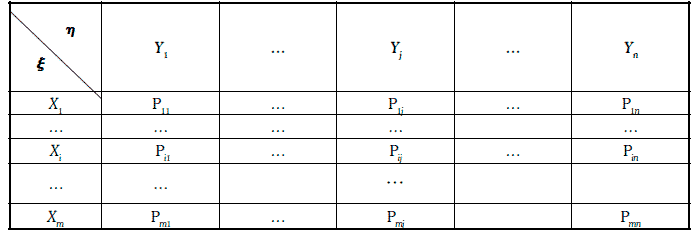
Равенство (1.69) позволяет каждому случайному числу приписать определенную пару значений случайных величин ξ и η. Такой процесс приписывания значений паре случайных величин (ξ, η) называют разыгрыванием этой пары.

Если случайные величины ξ и η независимы, то для разыгрывания пары (ξ, η) достаточно разыграть каждую случайную величину в отдельности. Для разыгрывания непрерывной случайной величины можно вначале найти дискретную случайную величину, близкую к данной случайной величине, а затем разыграть эту дискретную случайную величину.

Метод Монте-Карло позволяет численно находить различные вероятностные характеристики случайной величины η, зависящей от большого числа других случайных величин ξ1, ξ2…., ξn. Этот метод сводится к следующему: разыгрывается последовательность случайных величин (ξ1, ξ2…., ξn), для каждого розыгрыша определяется соответствующее значение случайной величины η, а по найденным значениям строится эмпирическое распределение вероятностей этой случайной величины.

Пример 1.67 [5]. Инвестор владеет портфелем, состоящим из одной казначейской облигации и двух корпоративных облигаций одного и того же кредитного рейтинга. Основные параметры портфеля указаны в таблице:

Инвестора интересует реализуемая доходность портфеля облигаций за 6 месяцев. По его мнению, реализуемая доходность портфеля будет определяться следующими двумя факторами: кривой доходностей казначейских облигаций через 6 месяцев и спредом между доходностями корпоративных и казначейских облигаций. Предположим, что инвестор располагает еще и следующей информацией:

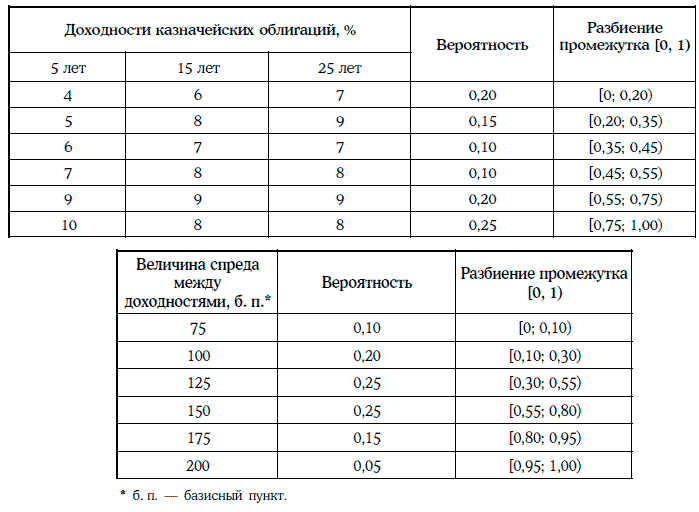
Для определения реализуемой доходности портфеля облигаций можно использовать метод Монте-Карло.

Первая итерация (случайные числа: 0,91 для кривой доходностей и 0,12 для спреда между доходностями). В этом случае доходности казначейских облигаций со сроком до погашения 5, 15 и 25 лет составят соответственно 10, 8 и 8 %, а доходности корпоративных облигаций со сроком до погашения 15 и 25 лет – 9 и 9 %.

Тогда цены облигаций (на номинал в 100 долл.) через 6 месяцев определяются следующим образом:

Предположим, что было проведено 100 итераций. При этом оказалось, что наименьшая реализуемая доходность портфеля равна -3,905 %, а наибольшая реализуемая доходность составляет 24,97 %.

Разделив отрезок [-3,905 %; 24,97 %] на достаточно большое число частей, подсчитаем для каждой части число итераций, дающих реализуемую доходность из этой части.

Таким образом, будет построено эмпирическое распределение вероятностей реализуемой доходности портфеля облигаций. После чего можно получить различные числовые характеристики этой реализуемой доходности: среднее значение, стандартное отклонение и т. д.

1.26. Случайные процессы и их основные характеристики

Дано основное вероятное пространство

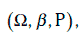
где Ω – пространство элементарных событий;

β – σ-алгебра случайных событий;

Р – вероятностная мера.

Рассмотрим некоторое числовое множество V, элементы которого в дальнейшем будем считать моментами времени.

Функция ξ(w, t) двух переменных w ∈ Ω и t ∈ V называется случайным процессом (stochastic process), определенным на множестве V, если для любых t ∈ V и x ∈ R (R – множество всех действительных чисел) множество

т. е. является случайным событием.

Из условия (1.70) следует, что если на множестве V определен случайный процесс ξ(w, t), то каждому моменту времени t ∈ V поставлена в соответствие случайная величина ξt(w) = ξ(w, t). Случайная величина ξt(w) называется сечением случайного процесса в момент времени t.

Таким образом, чтобы на множестве V задать некоторый случайный процесс, достаточно каждому моменту времени t ∈ V поставить в соответствие ту или иную случайную величину ξt(w) – сечение этого случайного процесса. В силу этого случайный процесс можно обозначить как ξt(w) или просто ξt.

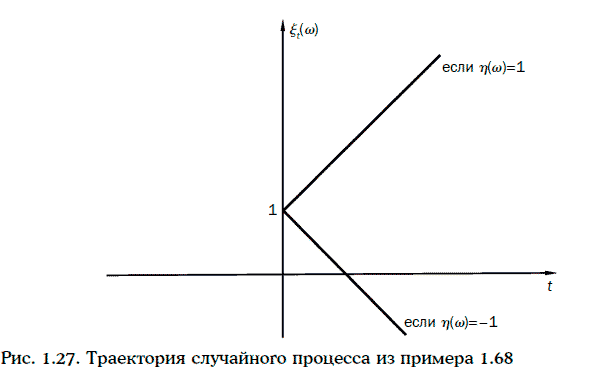
Если на множестве V задан случайный процесс ξ(w, t), то при каждом фиксированном элементарном событии w ∈ Ω мы имеем функцию одного переменного t. Эту функцию, определенную на множестве V, называют траекторией, или реализацией, случайного процесса ξ(w, t).

Пример 1.68. Рассмотрим случайный процесс

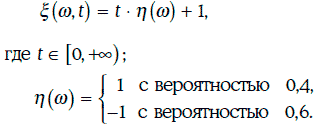
Сечением данного случайного процесса в момент времени t = 2 является случайная величина 2η(w) + 1. Траектории случайного процесса ξ(w, t) изображены на рис. 1.27.

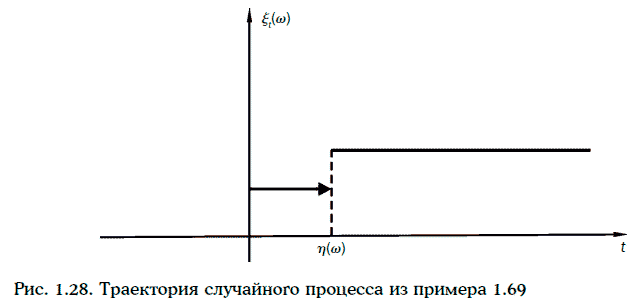
Пример 1.69. Случайный процесс на [0, +∞) определен следующим образом:

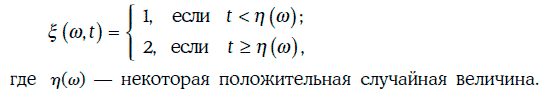
Сечением случайного процесса ξ(w, t) в момент времени t является случайная величина, принимающая значение 1 с вероятностью, равной P{η(w) > t}, и значение 2 с вероятностью, равной P{η(w) ≤ t}.

Траектория случайного процесса ξ(w, t) имеет вид, изображенный на рис. 1.28. Важнейшими характеристиками случайных процессов являются математическое ожидание и дисперсия.

Пример 1.70. Найдем математическое ожидание и дисперсию случайного процесса из примера 1.68.

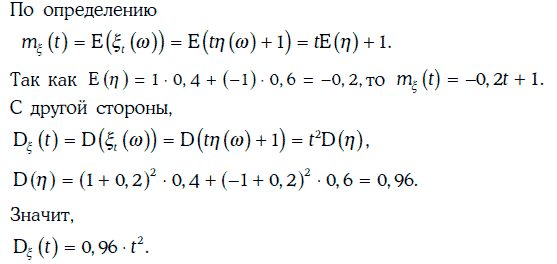
Пример 1.71. Рассмотрим случайный процесс из примера 1.69, считая, что случайная величина η(w) распределена показательно с плотностью

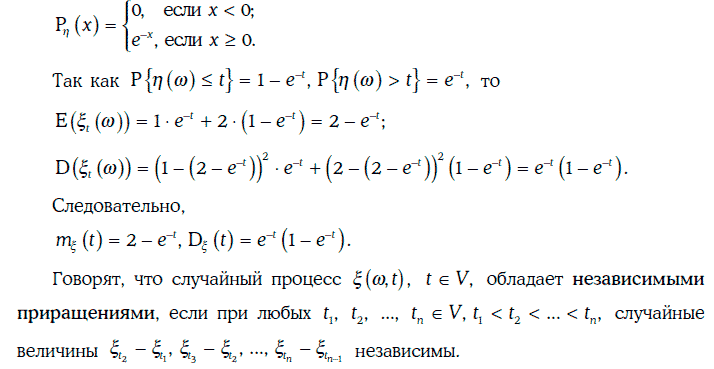
Случайные процессы с независимыми приращениями играют важную роль при моделировании эволюции финансовых показателей. Это объясняется тем, что финансовый рынок принято считать эффективным (efficient), если цены активов на этом рынке полностью отражают всю имеющуюся информацию об этих активах. На эффективном финансовом рынке изменения цен активов могут происходить только из-за появления новой информации (которая, вообще говоря, непредсказуема). Это означает, что изменения цены активов на таком рынке должны быть в некотором смысле независимы.

1.27. Важнейшие виды случайных процессов

1.27.1. Случайное блуждание

Сечением случайного блуждания в момент времени t0 + kh является дискретная случайная величина, закон распределения вероятностей которой имеет вид:

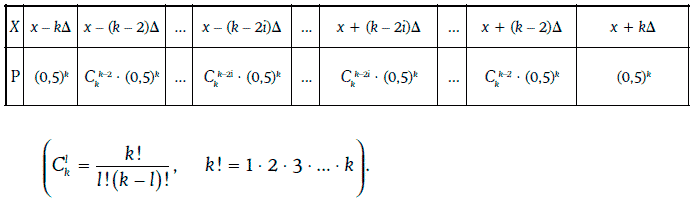
Траектории случайного блуждания изображены на рис. 1.29 (точками выделена одна из траекторий).

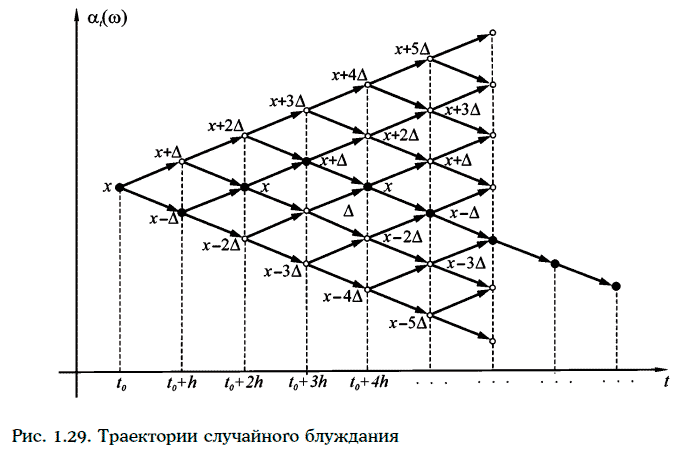
Случайное блуждание α (w, t) обладает независимыми приращениями, причем

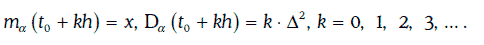
1.27.2. Биномиальная модель

Случайный процесс β(w, t), определенный на множестве

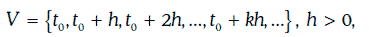
называется биномиальной моделью (binominal model), если

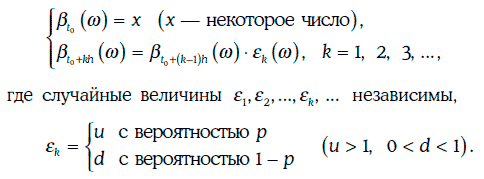
Сечением биномиальной модели в момент времени t0 + kh является дискретная случайная величина, закон распределения вероятностей которой имеет вид:

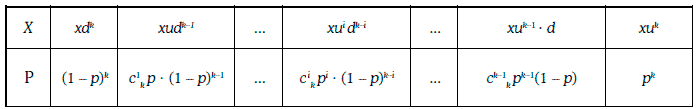
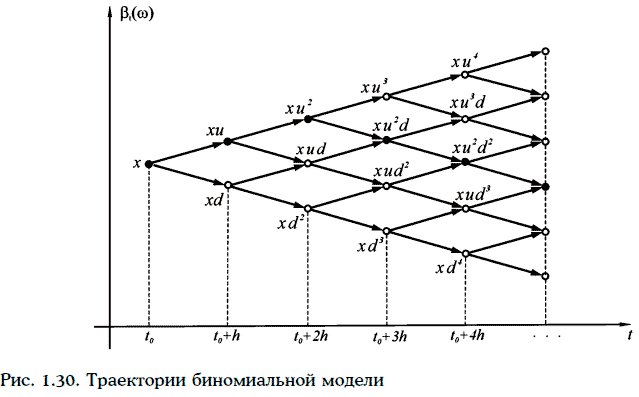
Траектории биноминальной модели изображены на рис. 1.30.

Если случайный процесс β (w, t) является биномиальной моделью с параметрами u, d, p, то

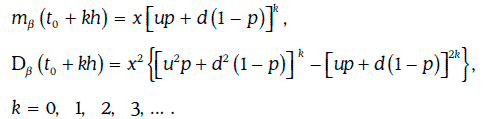
Приращения биномиальной модели, вообще говоря, не являются независимыми. Однако случайный процесс ln β (w, t) имеет независимые приращения.

Случайное блуждание и биноминальная модель относятся к случайным процессам с дискретным временем (discrete time process). Важнейшим примером случайного процесса с непрерывным временем (continuous time process) является винеровский случайный процесс.

1.27.3. Винеровский случайный процесс

Случайный процесс w(w, t), определенный на промежутке [t0, +∞), называется винеровским случайным процессом (Wienerprocess), если выполняются следующие условия:

Для моделирования траекторий винеровского случайного процесса w (w, t) на заданном промежутке времени [t0, Т] можно применить метод Монте-Карло.

Сам винеровский случайный процесс редко используется для моделирования финансовых показателей, так как имеет постоянное математическое ожидание. Однако на основе винеровского процесса строятся почти все случайные процессы, используемые в настоящее время для моделирования различных финансовых показателей.

1.28. Понятие о стохастических дифференциальных уравнениях

Стохастическим дифференциальным уравнением (stochastic differential equation) называется уравнение вида

Решением стохастического дифференциального уравнения (1.71) на промежутке [t, Т] называется случайный процесс х (w, τ), удовлетворяющий следующим условиям:

Любое решение стохастического дифференциального уравнения (1.71), удовлетворяющее некоторому начальному условию

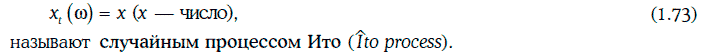
В частности, геометрическим броуновским движением (geometric Brownian motion) является случайный процесс, удовлетворяющий стохастическому дифференциальному уравнению:

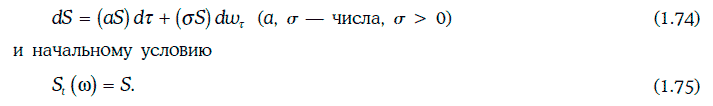
Геометрическое броуновское движение, определяемое условиями (1.74) и (1.75), можно найти в явном виде:

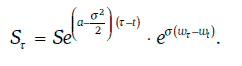
Во многих случаях можно считать, что эволюция цены финансовых активов описывается геометрическим броуновским движением. Такое моделирование оказывается достаточно точным, например, в случае обыкновенных акций.

Пример 1.72. Инвестор считает, что цена бездивидендной акции описывается геометрическим броуновским движением с коэффициентом смещения 0,1 и годовой волатильностью 40 %. В данный момент времени цена акции равна 100 долл. Инвестора интересует цена этой акции через месяц.

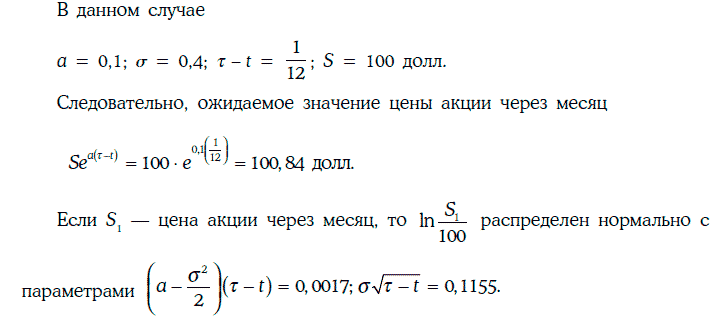
Эволюцию цены Вτ облигации с нулевым купоном можно описывать с помощью геометрического броуновского движения, лишь когда до погашения облигации остается достаточно много времени. Действительно, в момент погашения Т ее цена всегда равна номиналу, т. е. известна достоверно. Это означает, что

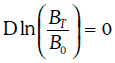
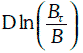
Таким образом, при моделировании эволюции цены облигации с нулевым купоном необходимо учитывать эффект приближения к номиналу (pull to par), а геометрическое броуновское движение этот эффект не учитывает, так как

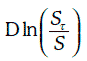
В общем случае найти решение стохастического дифференциального уравнения (1.71) в явном виде не удается. Поэтому для моделирования траекторий случайного процесса Ито часто применяется метод Монте-Карло.