Энциклопедия финансового риск-менеджмента

где D – дюрация Маколея,
r – требуемая доходность при начислении процентов дважды в год.
Имеет место следующее равенство:
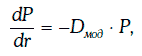
т. е. производная цены финансового инструмента по требуемой доходности равна произведению модифицированной дюрации этого инструмента на его цену с обратным знаком.
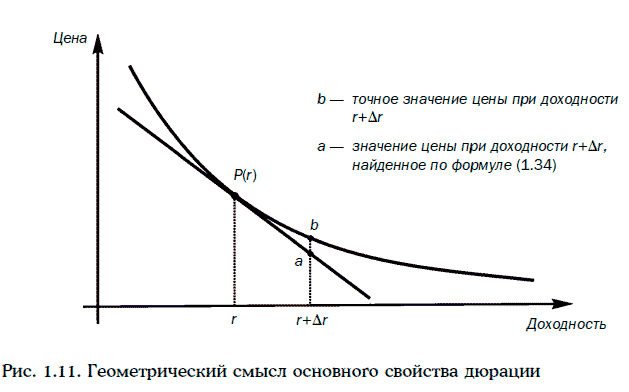
Основное свойство дюрации – при малых изменениях требуемой доходности имеет место равенство

Геометрическая иллюстрация равенства (1.34) приведена на рис. 1.11.

Расчет дюрации финансового инструмента при требуемой доходности 10 % приведен в таблице:
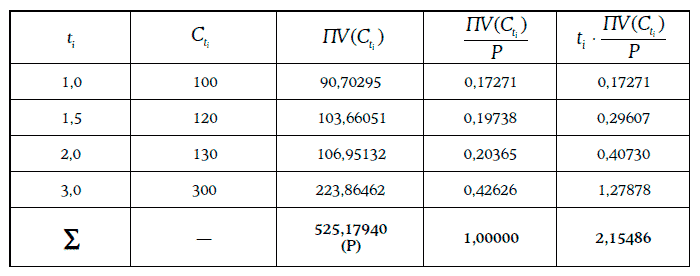
Таким образом, дюрация Маколея финансового инструмента равна 2,155 года.
Тогда модифицированная дюрация находится следующим образом:
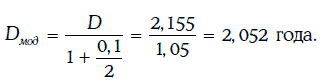
Если требуемая доходность увеличится на 10 базисных пунктов, то
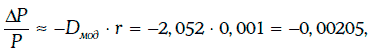
т. е. цена финансового инструмента упадет на 0,2 %.
Если же требуемая доходность мгновенно упадет на 200 базисных пунктов, то цена финансового инструмента вырастет приблизительно на 4,104 %, так как
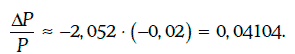
Точные значения относительного изменения цены финансового инструмента в этих двух случаях соответственно равны -0,002049 и 0,04222.
Дюрацию обыкновенной ренты с полугодовыми платежами можно найти по формуле:

где r – требуемая доходность (при начислении процентов дважды в год);
n – число платежей ренты.
В частности, дюрация бессрочной ренты определяется равенством

Дюрация Маколея облигации с полугодовыми купонами, когда до ее погашения остается в точности п полугодовых периодов, может быть найдена по формуле

где r – требуемая доходность при начислении процентов дважды в год;
f – купонная ставка облигации;
H – отношение приведенной стоимости ренты из купонных платежей к цене облигации.
Пример 1.35. Дана 7 %-ная облигация с полугодовыми купонами, когда до ее погашения остается 20 лет, а требуемая доходность – 10 %.
В данном случае r = 0,1, f = 0,07, n = 40, q = 3,50 долл.
Приведенная стоимость ренты из полугодовых купонных платежей может быть найдена следующим образом:
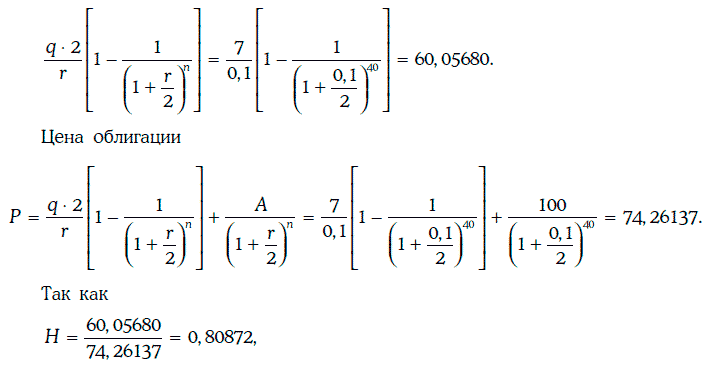
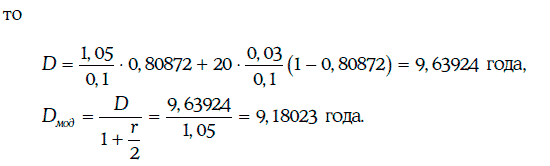
Для расчета модифицированной дюрации любого финансового инструмента с заданным потоком платежей можно использовать следующую приближенную формулу:

Пример 1.36. Рассмотрим облигацию из примера 1.35. Точное значение модифицированной дюрации этой облигации 9,18023 года. Найдем модифицированную дюрацию с помощью приближенной формулы (1.38) при Δу = 20 базисных пунктов.
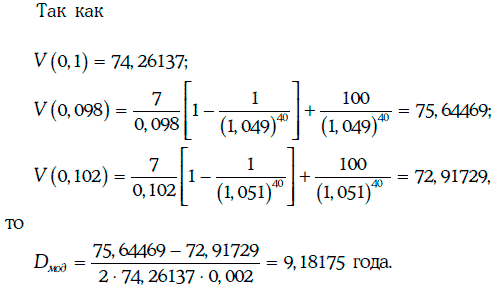
Основные утверждения о дюрации Маколея для купонных облигаций с полугодовыми купонами, когда до очередного купонного платежа остается 6 месяцев:
1. Дюрация любой купонной облигации не превышает срока до ее погашения, а дюрация облигации с нулевым купоном всегда совпадает со сроком до ее погашения.
2. Если купонная ставка облигации отлична от нуля, то чем больше требуемая доходность, тем меньше дюрация.
3. Если до погашения облигации остается более одного купонного периода, то чем выше купонная ставка при неизменной требуемой доходности, тем меньше дюрация.
4. Чем меньше времени остается до погашения облигации при прочих неизменных факторах, тем меньше дюрация (за исключением долгосрочных облигаций, продающихся с дисконтом).
1.14. Модифицированная дюрация портфеля облигаций
Модифицированной дюрацией портфеля облигаций называют взвешенную по стоимости сумму модифицированных дюраций облигаций, входящих в этот портфель, т. е.

Основное свойство модифицированной дюрации портфеля облигаций: если требуемые доходности всех облигаций портфеля изменяются на одну и ту же достаточно малую величину, имеет место следующее приближенное равенство:

Пример 1.37. Рассмотрим портфель, состоящий из трех облигаций с полугодовыми купонами при требуемой доходности 10 % со следующими данными:
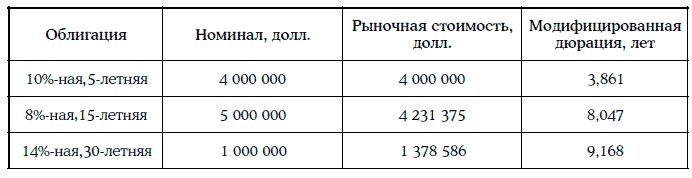
В данном случае начальная стоимость портфеля П = 9 609 961 долл. Тогда
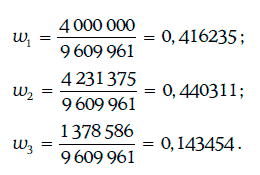
Следовательно, модифицированная дюрация портфеля облигаций составляет
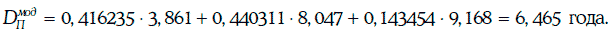
Если требуемые доходности мгновенно увеличатся на 60 базисных пунктов, то
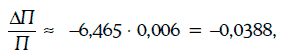
т. е. цена портфеля упадет на 3,88 %.
Точное изменение цены портфеля равно -0,0376, т. е. -3,76 %.
Говорят, что инвестор занимает длинную позицию (long position) на рынке облигаций, если он купил некоторую облигацию на этом рынке.
Если же инвестор взял облигацию взаймы у дилера и продал ее на рынке, то говорят, что на рынке облигаций он занимает короткую позицию (short position). Инвестор, занимающий короткую позицию, обязан в определенный момент времени в будущем вернуть облигацию дилеру и выплатить компенсацию за недополученные купонные платежи. Рассмотрим на примере, как определить модифицированную дюрацию портфеля, состоящего из длинных и коротких позиций на рынке облигаций.
Пример 1.38. Портфель состоит из двух позиций: длинной позиции в размере 100 млн долл. по двухлетней облигации ценой 101 долл. с модифицированной дюрацией 1,7 и короткой позиции в размере 50 млн долл. по 5-летней облигации ценой 99 долл. с модифицированной дюрацией 4,1. Определим модифицированную дюрацию этого портфеля.
Исходная стоимость портфеля может быть найдена следующим образом:

1.15. Приложения дюрации
1.15.1. Обмен облигаций
Предположим, что инвестор рассматривает вопрос об обмене облигации Х стоимостью VX с модифицированной дюрацией
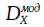
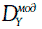
Выясним, каким должен быть номинал облигации Y, чтобы обмен облигации Х на облигацию Y не увеличивал подверженность инвестора процентному риску.
Если требуемая доходность облигации Х изменится на величину Δr, то соответствующее изменение стоимости этой облигации определяется равенством

Можно предположить, что на основе статистических исследований установлено, что при изменении требуемой доходности облигации Х на величину Δr требуемая доходность облигации Y изменяется на величину βΔr.
Тогда соответствующее изменение стоимости облигации Y можно найти по формуле:

где Ay – номинал облигации Y.
Обмен облигаций не будет увеличивать подверженность процентному риску, если при любом Δr
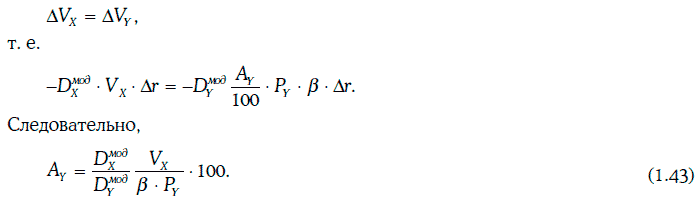
Равенство (1.43) показывает, каким должен быть номинал облигации Y, чтобы при обмене облигации Х на облигацию Y не увеличивался процентный риск.
Пример 1.39. Инвестор рассматривает вопрос об обмене облигации Х стоимостью 8 млн долл. на облигацию Y при цене PY = 96 долл. Модифицированные дюрации облигаций Х и Y равны 5 и 4 соответственно, а коэффициент β равен 1,6.
Чтобы при обмене не менялась подверженность процентному риску, номинал облигации Y должен удовлетворять равенству:
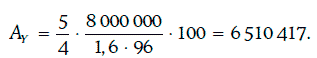
Таким образом, искомый номинал облигаций Y должен равняться 6 510 417.
1.15.2. Иммунизация портфеля облигаций
Предположим, что в данный (нулевой) момент времени инвестор владеет портфелем облигаций, который он собирается продать через Т лет.
Если в данный момент времени все рыночные доходности одинаковы, т. е. кривая доходности имеет ровный вид, то будущая стоимость инвестиций ПА(Т) через Т лет определяется следующим образом:
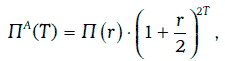
где r – рыночная доходность,
П(r) – стоимость портфеля при рыночной доходности, равной r.
Будущую стоимость ПА(Т) будем называть целевой накопленной стоимостью портфеля облигаций.
Однако если между данным моментом времени и первым процентным платежом рыночные доходности изменяются на одну и ту же величину Δr, а в дальнейшем уже меняться не будут, то будущая стоимость инвестиции Пф(Т) через Т лет удовлетворяет равенству
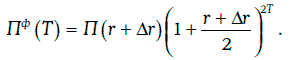
Будущую стоимость Пф(Т) будем называть фактической накопленной стоимостью портфеля облигаций.
Фактическая накопленная стоимость портфеля облигаций может оказаться выше или ниже целевой накопленной стоимости этого портфеля. Однако если временной горизонт инвестора Т совпадает с дюрацией Маколея портфеля облигаций, то фактическая накопленная стоимость портфеля никогда не будет меньше его целевой накопленной стоимости.
Пример 1.40. Рассмотрим портфель из двух облигаций с полугодовыми купонами, когда все рыночные доходности равны 6 %. Основные данные об облигациях портфеля приведены ниже в таблице:

Дюрация Маколея данного портфеля облигаций находится следующим образом:
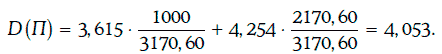
Целевая накопленная стоимость портфеля через 4,053 года будет равна:
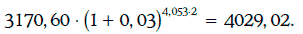
В таблице указаны фактические накопленные стоимости через 4,053 года при различных изменениях рыночных доходностей:

Стратегия иммунизации портфеля облигаций рассчитана на защиту портфеля облигаций от процентного риска. Эта стратегия предполагает следующие действия. В начальный момент времени формируется портфель облигаций так, чтобы дюрация Маколея этого портфеля совпадала с временным горизонтом инвестора. С годами портфель периодически пересматривается так, чтобы каждый раз дюрация Маколея совпадала с временным горизонтом инвестора.
1.16. Выпуклость финансовых инструментов
Рассмотрим финансовый инструмент со следующим потоком платежей:

Если требуемая доходность при начислении процентов дважды в год равна r, то выпуклостью (convexity) данного финансового инструмента называют число
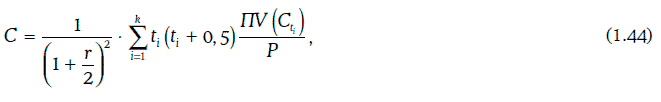

Имеет место следующее равенство:
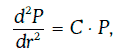
т. е. производная второго порядка цены финансового инструмента по требуемой доходности равна произведению выпуклости этого финансового инструмента на его цену.
Основное свойство выпуклостиПри малых изменениях требуемой доходности имеет место следующее приближенное равенство:

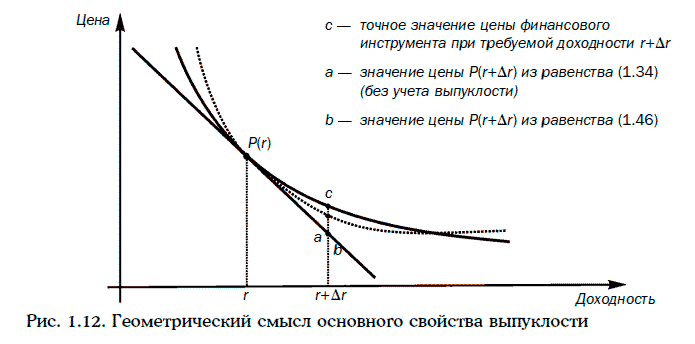
Равенство (1.45) можно переписать в следующем виде:
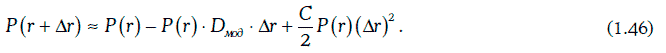
Геометрический смысл этого равенства проиллюстрирован рис. 1.12.
Пример 1.41. Финансовый инструмент характеризуется следующим потоком платежей:
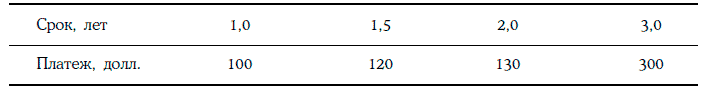
Расчет выпуклости данного финансового инструмента при требуемой доходности 10 % приведен в таблице:
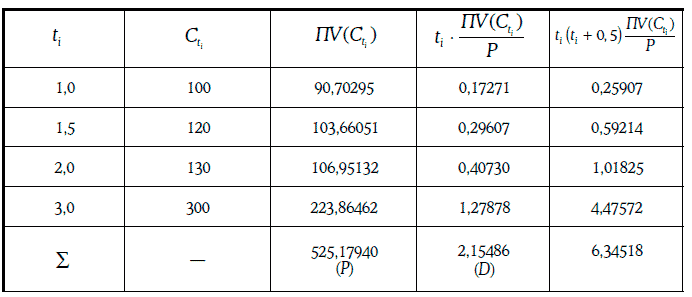
Модифицированная дюрация финансового инструмента
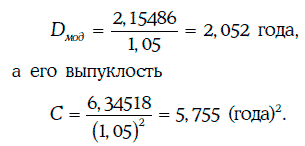
Если требуемая доходность в начальный момент времени увеличится на 50 базисных пунктов, то цена финансового инструмента упадет приблизительно на 1,0188 %, так как
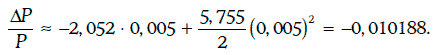
Заметим, что относительное изменение цены финансового инструмента, найденное приближенно, без учета выпуклости, равно -0,01026, а точное значение этого изменения равно -0,010189.
Если же требуемая доходность в начальный момент времени упадет на 200 базисных пунктов, то цена финансового инструмента вырастет приблизительно на 4,219 %, так как
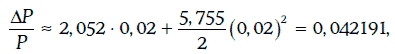
в то время как относительное изменение цены инструмента, найденное приближенно, без учета выпуклости, равно 0,04104, а точное значение этого изменения равно 0,04222.
Основные утверждения о выпуклости финансовых инструментов1. Произведение начальной цены финансового инструмента на его модифицированную дюрацию называют долларовой дюрацией (dollar duration) этого инструмента. Производная долларовой дюрации финансового инструмента по требуемой доходности равна произведению выпуклости этого финансового инструмента на его цену с обратным знаком, т. е.
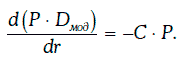
Это означает, что выпуклость финансового инструмента является мерой скорости изменения долларовой дюрации этого инструмента.
2. При уменьшении требуемой доходности растут модифицированная дюрация и выпуклость финансового инструмента, причем
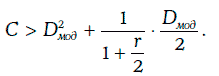
3. Если финансовый инструмент имеет одинаковые модифицированные дюрации, то при достаточно малом изменении требуемой доходности у финансового инструмента с большей выпуклостью относительный рост цены больше, а относительное снижение цены – меньше. Это означает, что при одной и той же модифицированной дюрации для инвесторов более привлекателен финансовый инструмент с большей выпуклостью.
4. При заданных требуемой доходности и сроке до погашения купонной облигации: чем меньше купонная ставка, тем больше выпуклость.
Для оценки выпуклости любого финансового инструмента можно использовать следующую приближенную формулу:

Пример 1.42. Рассмотрим 7 %-ную облигацию с полугодовыми купонами, когда до ее погашения остается 3 года, а требуемая доходность равна 10 %.
Оценим выпуклость данной облигации с помощью приближенной формулы (1.47), считая, что номинал облигации равен 100 долл. Изменение требуемой доходности выберем в 20 базисных пунктов (Δу = 0,002). Тогда

Расчет точного значения выпуклости данной облигации приведен в таблице:
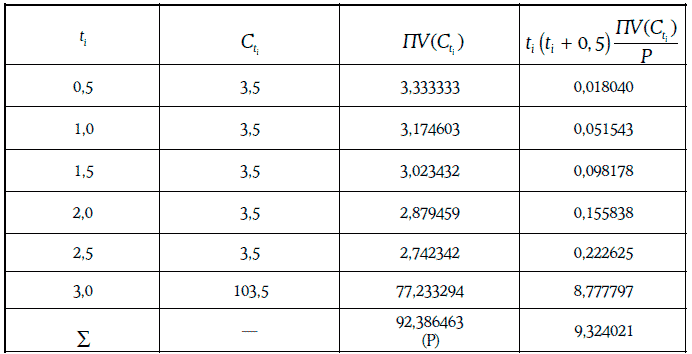
Значит,
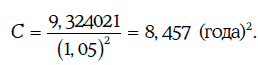
Таким образом, приближенная формула (1.47) дает достаточно хорошую оценку выпуклости облигации.
1.17. Выпуклость портфеля облигаций
Выпуклостью портфеля облигаций называют взвешенную по стоимости сумму выпуклостей облигаций, из которых составлен этот портфель, т. е. по определению


Если требуемые доходности облигаций портфеля изменяются на одну и ту же величину, то имеет место следующее приближенное равенство:

Заметим, что равенство (1.49) соблюдается тем точнее, чем меньше Δr (по абсолютной величине).
На основе равенства (1.49) можно сделать следующий вывод о роли выпуклости портфеля облигаций как меры процентного риска: если портфели облигаций имеют одну и ту же модифицированную дюрацию, то у портфеля с большей выпуклостью относительный рост цены больше, а относительное снижение цены – меньше.
Однако это утверждение справедливо лишь в том случае, когда требуемые доходности облигаций портфеля изменяются на одну и ту же величину.
Пример 1.43 [5]. Даны три облигации с полугодовыми купонами, основные показатели которых приведены в таблице:
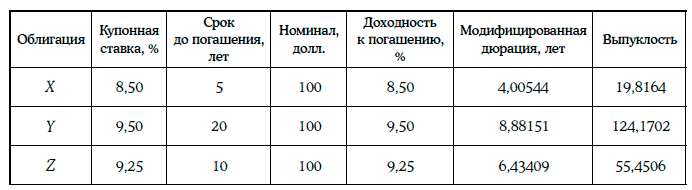
Из данных облигаций сформируем два портфеля: портфель А (50,2 % – облигация Х и 49,8 % – облигация Y), портфель В (облигация Z).
Модифицированная дюрация и выпуклость портфеля А находятся следующим образом:
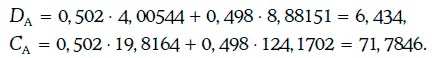
Таким образом, дюрации портфелей А и В одинаковы, а выпуклость портфеля А выше выпуклости портфеля В.
Относительные изменения стоимостей портфелей А и В при различных изменениях требуемых доходностей облигаций на одну и ту же величину приведены в следующей таблице:
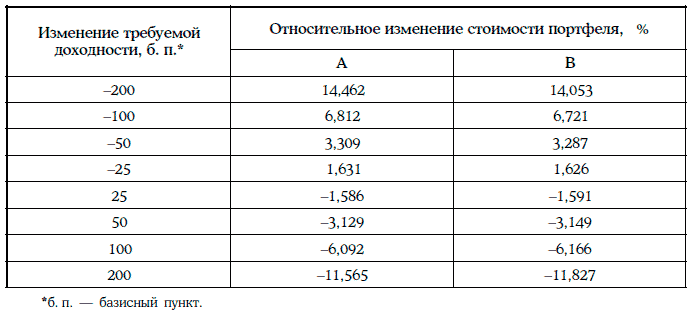
Таким образом, при различных параллельных сдвигах кривой доходностей относительное изменение стоимости портфеля А всегда больше относительного изменения стоимости портфеля В.
При непараллельных сдвигах кривой доходностей (yield curve twist), т. е. когда требуемые доходности изменяются по-разному, ситуация может оказаться противоположной. В частности, если требуемые доходности облигаций Х, Y и Z уменьшаются на 75, 25 и 50 б. п. соответственно, то относительные изменения стоимостей портфелей А и В будут равны 2,662 и 3,287 %, т. е. относительный рост стоимости портфеля А окажется ниже относительного роста стоимости портфеля В.
Основные характеристики портфеля облигаций – средневзвешенная (или внутренняя) доходность, модифицированная дюрация и выпуклость – используются для сравнения портфеля облигаций с точки зрения их инвестиционного качества.
Однако эти характеристики не всегда дают возможность сделать правильный вывод.
Пример 1.44 [5]. Рассмотрим портфели А и В из предыдущего примера 1.43. Основные характеристики этих портфелей приведены в таблице:

Для сравнения портфелей А и В воспользуемся показателем, называемым годовой реализуемой доходностью за 6 месяцев.
В данном случае годовая реализуемая доходность за 6 месяцев портфелей А и В может быть найдена по формуле:

В таблице показаны разности годовых реализованных доходностей портфелей А и В (RB – RA) при различных сдвигах кривой доходностей:
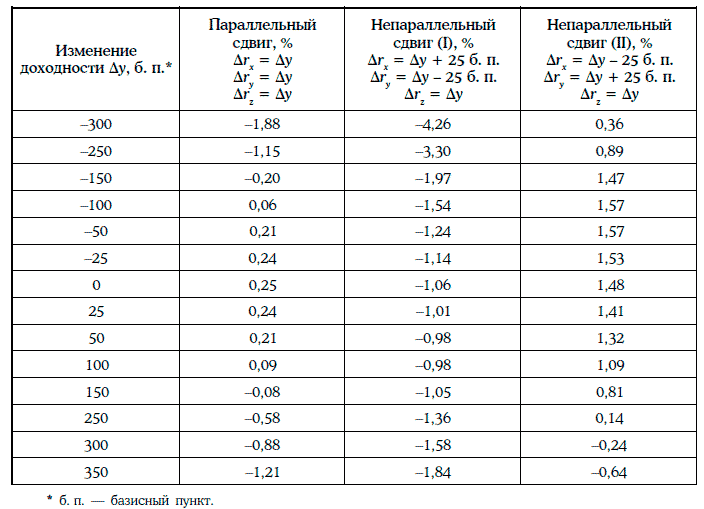
Таким образом, инвестиционная эффективность не определяется основными характеристиками портфелей А и В, а зависит от того, какие изменения требуемых доходностей происходят на рынке.
1.18. Множества. Операции над множествами
Множество (set) – это совокупность некоторых объектов. Объекты, из которых состоит множество А, называют элементами этого множества.
Если а является элементом множества А, то пишут а ∈ А.
Задать множество можно, либо перечислив все его элементы, либо указав характеристическое свойство, которому должны удовлетворять все элементы этого множества.
Например, запись А = {a1, a2, a3, a4} означает, что множество А состоит из элементов a1, a2, a3, a4.
Множество В всех действительных чисел, удовлетворяющих неравенству х2 – 2х + 3 ≤ 0, можно записать следующим образом:
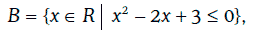
где R – множество всех действительных чисел.
Множество А называют подмножеством (subset) множества В, если каждый элемент множества А является элементом множества В (рис. 1.13).
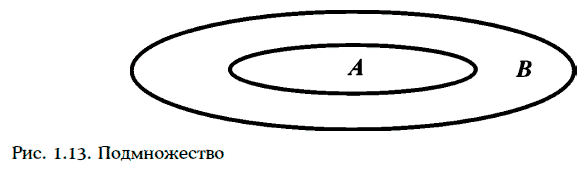
Если множество А является подмножеством множества В, то пишут А ⊂ В. Например, множество А = {1, 2, 3} является подмножеством множества В = {1, 2, 3, 4, 5}. Множество Z всех целых чисел является подмножеством множества R всех действительных чисел.
Разностью А\В двух множеств А и В называют множество всех элементов А, не попавших в множество В (рис. 1.14).
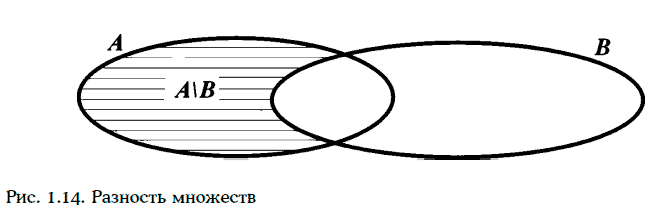
Если В ⊂ А, то разность А\В называют дополнением множества В до множества А. Например, если А = {1, 2, 3, 4}, а В = {3, 4, 5, 6}, то А\В = = {1, 2}.
Пересечением двух множеств А и В называют множество, обозначаемое А ∩ B, все элементы которого принадлежат как множеству А, так и множеству В (рис. 1.15).
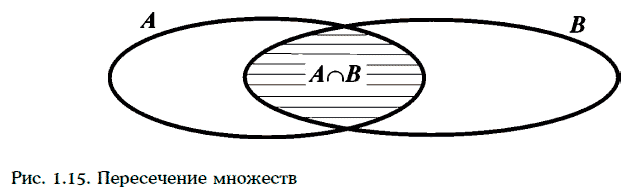
Например, если А = {1, 2, 3}, а В = {1, 3, 4, 5}, то А ∩ В = {1, 3}.
Если множества А и В не содержат общих элементов, то говорят, что они не пересекаются, и пишут A ∩ B = ∅ (∅ – символ пустого множества).
Аналогично можно определить пересечение трех, четырех и более множеств. В частности, множество
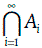
Объединением двух множеств А и В называют множество, обозначаемое А ∪ B, все элементы которого принадлежат хотя бы одному из множеств А и В (рис. 1.16).
Например, если А = {1, 2, 3, 4}, а В = {3, 4, 5, 6}, то А ∪ В = {1, 2, 3, 4, 5, 6}. Точно так же определяется объединение трех, четырех и более множеств. В частности, множество