
Рынок облигаций. Анализ и стратегии

Результат представляет собой сумму купонных выплат и процента на процент на момент окончания второго года (через четыре периода). Реинвестируем эту сумму под 4 % на период до окончания инвестиционного горизонта, т. е. на четыре года (восемь периодов); $191,09 возрастут до:
$191,09 × 1,048 = $261,52.Для последних восьми купонных выплат сумма купонных выплат и процента на процент, при условии полугодовой ставки реинвестиций 5 %, составит:

Купонные выплаты плюс процент на процент для всех 12 периодов составят $691,23 (т. е. $261,52 + $429,71).
Этап 2. Предполагаемая цена продажи облигации при условии требуемой доходности 10,6 % равна $922,31[17].
Этап 3. Общее будущее количество денег равно $1613,54 ($691,23 + $922,31).
Этап 4. Проведем следующие вычисления:
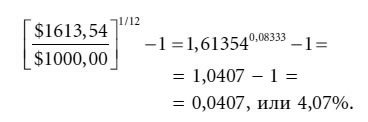
Этап 5. Удвоим 4,07 % и получим общую прибыль в процентах годовых, равную 8,14 %.
Анализ облигации с помощью меры общей прибыли (анализ временных горизонтов)
Мера общей прибыли позволяет, исходя из собственных предположений о будущих ставках реинвестиций и будущей требуемой доходности, оценить эффективность вложения в облигацию на данном временном горизонте. Таким образом, управляющий портфелем получает возможность выбрать из нескольких возможных кандидатов облигацию, которая на запланированном временном горизонте покажет наилучший результат. Еще раз обратим ваше внимание на то, что доходность к погашению не может выполнять аналогичные функции, т. е. не является мерой относительной ценности облигации.
Использование величины общей прибыли при анализе эффективности вложений в облигацию на данном отрезке времени – процедура, лежащая в основе так называемого анализа временных горизонтов. Общая прибыль, вычисленная для данного временного горизонта, получила название прибыли на временно́м горизонте (horizon return). В нашей книге термины «прибыль на временном горизонте» и «общая прибыль» взаимозаменяемы.
Анализ временных горизонтов используется и при изучении инвестиционных характеристик облигационных свопов. Облигационный своп предполагает обмен имеющейся в портфеле облигации на другую облигацию. В ситуации, когда цель облигационного свопа – увеличить прибыль от портфеля на запланированном временном горизонте, управляющий может подсчитать общую прибыль облигации, которую собирается приобрести, и сравнить результат с общей прибылью облигации, имеющейся в портфеле; таким образом производится оценка целесообразности замены. Конкретные стратегии облигационных свопов будут обсуждаться в главе 25.
Противники меры общей прибыли недовольны тем, что, применяя ее, портфельный менеджер вынужден строить предположения относительно ставок реинвестиций и будущих доходностей, а также мыслить в категориях инвестиционного горизонта. К сожалению, часть управляющих портфелями предпочитают работать с доходностью к погашению и доходностью к колл-опциону только потому, что вычисление этих величин не требует от них формулировки собственных прогнозов рынка. Между тем анализ временных горизонтов позволяет оценить облигацию в контексте разных рыночных сценариев, разных ставок реинвестиций и требуемых доходностей. Только изучив несколько сценариев, менеджер может понять, насколько чувствительна облигация к разным типам происходящих на рынке изменений. В главе 20 мы поговорим о том, каким образом включается в анализ информация о предполагаемых изменениях процентных ставок.
Измерение изменений доходности
Когда процентные ставки или доходности меняются между двумя временными периодами, на практике существует два способа представления изменений: в абсолютном выражении и в процентном выражении.
Абсолютное изменение доходности (которое также называют абсолютным изменением ставки) измеряется в базисных пунктах и является абсолютным значением разницы между двумя доходностями. То есть
абсолютное изменение доходности (в базисных пунктах) =[первоначальная доходность – новая доходность] × 100Например, рассмотрим три следующие доходности за три месяца:
Месяц 1 4,45 %Месяц 2 5,11 %Месяц 3 4,82%Тогда абсолютное изменение доходности рассчитывается, как показано ниже:
абсолютное изменение доходности с месяца 1 по месяц 2 = [4,45 % – 5,11 %] × 100 = 66 базисных пунктовабсолютное изменение доходности с месяца 2 по месяц 3 = [5,11 % – 4,82 %] × 100 = 29 базисных пунктовПроцентное изменение доходности рассчитывается как натуральный логарифм изменения доходности, как показано ниже:
процентное изменение доходности = 100 × ln (новая доходность/первоначальная доходность)где ln – натуральный логарифм.
Для указанных ранее доходностей за три месяца процентные изменения доходности составят:
абсолютное изменение доходности с месяца 1 по месяц 2 = ln(5,11 % / 4,45 %) – 13,83 % абсолютное изменение доходности с месяца 2 по месяц 3 = ln(4,82 % / 5,11 %) = –5,84%Резюме
В этой главе мы описали традиционные меры доходности, широко используемые участниками рынка облигаций: текущую доходность, доходность к погашению, доходность к колл-опциону, доходность к пут-опциону, доходность к наихудшему и доходность денежного потока. Затем мы обратились к трем потенциальным источникам денежной прибыли от инвестирования в облигацию (купонные выплаты, доход от реинвестиций, прирост/потери капитала) и показали, что ни одна из традиционно принятых мер доходности не учитывает корректным образом все три компонента. Текущая доходность не принимает в расчет ни доход от реинвестиций, ни прирост/потери капитала. Доходность к погашению учитывает все три источника дохода, однако строится на безосновательном предположении о том, что купонные выплаты могут быть реинвестированы под данную доходность к погашению. Риск, связанный с реинвестированием купонных выплат под ставки более низкие, чем доходность к погашению, называется риском реинвестиций. Доходность к колл-опциону имеет аналогичные недостатки: предполагается, что купонные выплаты могут быть реинвестированы под доходность к колл-опциону. Величина доходности денежных потоков вычисляется на основании тех же предположений, что и доходность к погашению; кроме того, считается, что, во-первых, периодические выплаты номинала могут быть реинвестированы под доходность денежного потока и, во-вторых, предполагаемые предоплаты действительно будут иметь место. Наконец, нами была представлена еще одна мера доходности – общая прибыль, которая на основании предположений инвестора или портфельного менеджера о будущем состоянии рынка дает более полную информацию об относительной ценности облигации на запланированном временном горизонте.
Изменение доходности между двумя периодами времени можно рассчитать как абсолютное изменение доходности или как процентное изменение доходности.
Вопросы
1. Долговое обязательство обещает следующие выплаты:

Предположим, что цена данного долгового обязательства составляет $7704. Какова доходность или внутренняя ставка доходности, обещанная данным долговым обязательством?
2. Какова точная годовая ставка, если полугодовая процентная ставка равна 4,3 %?
3. Что такое доходность к погашению облигации?
4. Что такое доходность к погашению, эквивалентная облигационной?
5. а. Определите размер денежных потоков четырех облигаций, если известно, что каждая из них имеет номинальную стоимость $1000 и купон по ним выплачивается раз в полгода.

b. Вычислите доходность к погашению четырех облигаций.
6. Управляющий портфелем хочет купить одну из двух облигаций. Облигация А будет погашена через три года, купон равен 10 % и выплачивается раз в полгода. Облигация В имеет то же кредитное качество; ее срок до погашения – 10 лет, купон (выплачивается раз в полгода) – 12 %. Обе облигации торгуются по номиналу.
а. Предположим, что управляющий портфелем планирует держать облигацию три года. Какую из двух ценных бумаг ему лучше купить?
b. Предположим, что менеджер будет держать облигацию не три года, а шесть лет. Какую облигацию ему лучше приобрести в этом случае?
с. Допустим, что менеджер управляет активами страховой компании, которая выпустила пятилетний гарантированный инвестиционный контракт (GIC). Страховая компания обещала своим инвесторам выплачивать по 9 % каждые полгода. Какую из двух облигаций менеджер должен купить, чтобы страховая компания осуществила выплаты по GIC и в то же время получила прибыль?
7. Рассмотрим облигацию со следующими параметрами:
Купонная ставка = 11%
Длительность = 18 лет
Номинальная стоимость = $1000
Первый отзыв по номиналу (колл-опцион) – через 13 лет
Единственная дата продажи эмитенту (пут-опцион) – через пять лет; пут-опцион может быть исполнен по номиналу.
Предположим, что рыночная цена этой облигации равна $1169.
а. Докажите, что доходность к погашению этой облигации равна 9,077 %.
b. Докажите, что доходность к первому отзыву по номиналу равна 8,793 %.
с. Докажите, что доходность к пут-опциону равна 6,942 %.
d. Предположим, что регламент отзыва этой облигации таков:
Она может быть выкуплена через восемь лет по $1055.
Она может быть выкуплена через 13 лет по $1000.
Предположим также, что облигация может быть продана эмитенту в единственную дату через пять лет с настоящего времени, а ее доходность к первому отзыву по номиналу составляет 8,535 %. Какова доходность к наихудшему этой облигации?
8. а. Что такое амортизируемая ценная бумага? b. Назовите три компонента денежного потока амортизируемой ценной бумаги. с. Что такое доходность денежного потока?
9. Как вычисляется внутренняя ставка доходности портфеля?
10. Каковы недостатки внутренней ставки как меры доходности портфеля?
11. Предположим, что купонная ставка ценной бумаги с плавающей ставкой пересчитывается каждые полгода со спредом над референсной ставкой, равным 70 базисным пунктам. Допустим, что облигация торгуется по цене меньшей, чем номинал. Больше или меньше 70 базисных пунктов будет в этом случае дисконтный спред?
12. Инвестор собирается приобрести 20-летнюю облигацию с купоном 7 %, торгующуюся по $816 при номинале $1000. Доходность к погашению облигации равна 9 %.
а. Каково общее количество денег, полученное от вложения $816 на 20 лет под 9 % годовых, с учетом реинвестиций, производимых каждые полгода?
b. Какова сумма всех купонных выплат за время жизни облигации?
c. Каково общее количество денег, которое инвестор получит к моменту окончания 20-летнего срока от купонных выплат и выплаты номинала?
d. Допустим, что инвестор хочет получить общее количество денег, обозначенное в пункте а. Каков в этом случае должен быть размер процента на процент?
e. Вычислите величину процента на процент при условии, что полугодовые купонные выплаты могут быть каждые шесть месяцев реинвестированы под 4,5 %; заметим, что результат должен быть тот же, что и в пункте d.
13. Какова общая прибыль 20-летней облигации с нулевым купоном и доходностью к погашению 8 % при условии, что облигация додержана до погашения?
14. Объясните, почему величина общей прибыли облигации, додержанной до погашения, – число, располагающееся между значениями доходности к погашению и ставкой реинвестирования.
15. Как вы думаете, к какому из двух значений – доходность к погашению или ставка реинвестирования – окажется ближе общая прибыль долгосрочной высокодоходной купонной облигации, додержанной до погашения?
16. Предположим, что инвестор, запланировавший пятилетний инвестиционный горизонт, собирается купить по номиналу семилетнюю облигацию с 9 %-ным купоном. Инвестор считает, что сможет реинвестировать купонные выплаты под годовую ставку 9,4 %; кроме того, он полагает, что в момент окончания инвестиционного горизонта двухлетние облигации будут торговаться с доходностью к погашению 12 %. Какова общая прибыль облигации?
17. Два портфельных менеджера обсуждают инвестиционные характеристики амортизируемых ценных бумаг. Управляющий А полагает, что такие ценные бумаги выгоднее прочих, поскольку периодические выплаты наряду с купонными включают частичные выплаты номинала. Таким образом, вкладывая капитал в эти облигации, можно получить больший доход от реинвестиций. Кроме того, выплаты, как правило, производятся ежемесячно – доход от реинвестиций, соответственно, возрастает. Управляющий В думает, что необходимость каждый месяц совершать реинвестиции, превышающие купонные выплаты, – недостаток амортизируемых ценных бумаг. С кем вы согласны и почему?
18. Возьмем следующие доходности:
Неделя 1: 3,84%
Неделя 2: 3,51%
Неделя 3: 3,95%
а. Рассчитайте абсолютное изменение доходности и процентное изменение доходности с недели 1 по неделю 2.
б. Рассчитайте абсолютное изменение доходности и процентное изменение доходности с недели 2 по неделю 3.
Глава 4. ВОЛАТИЛЬНОСТЬ ЦЕН НА ОБЛИГАЦИИ
В этой главе читателю будут представлены сведения:
• о связи цены и доходности облигации без встроенных опционов;
• о факторах, определяющих волатильность цен при изменении доходностей;
• об общих выводах относительно волатильности цены облигации без встроенных опционов;
• о способе вычисления ценовой стоимости базисного пункта;
• о вычислении и интерпретации дюрации Маколея, модифицированной дюрации и долларовой дюрации облигации;
• о дюрации как мере чувствительности цены облигации к изменениям доходности;
• об измерении дюрации спреда облигации с фиксированной и плавающей ставкой;
• о вычислении дюрации портфеля и характеристиках портфельной дюрации;
• о недостатках дюрации как меры волатильности цены;
• о поправках, которые вносятся в значение дюрации как меры ценовых изменений с помощью понятия выпуклости;
• об аппроксимации значений дюрации и выпуклости облигации;
• о дюрации облигации с обратной плавающей ставкой;
• об измерении чувствительности портфеля к непараллельным изменениям процентных ставок (дюрации ключевых процентных ставок).
Разработка и использование эффективных стратегий управления портфелем облигаций невозможны без понимания сущности волатильности цен на облигации как реакции на изменения процентных ставок. Цель данной главы – объяснить понятие волатильности цены и представить несколько способов измерения волатильности.
СВЯЗЬ ЦЕНЫ И ДОХОДНОСТИ ДЛЯ ОБЛИГАЦИИ БЕЗ ВСТРОЕННЫХ ОПЦИОНОВ
Как следует из материалов главы 2, фундаментальным свойством облигаций без встроенных опционов является изменение цены в направлении, противоположном изменению требуемой доходности облигации. Феномен объясняется тождеством цены значению приведенной стоимости предполагаемых денежных потоков облигации. Рост (падение) требуемой доходности заставляет падать (расти) приведенную стоимость денежных потоков и тем самым уменьшает (увеличивает) цену. В табл. 4.1 приводятся соотношения доходности и цены шести гипотетических облигаций; цена указана для номинальной стоимости, равной $100, и купона, выплачиваемого раз в полгода.
1. Купон 9 %, длительность 5 лет.
2. Купон 9 %, длительность 25 лет.
3. Купон 6 %, длительность 5 лет.
4. Купон 6 %, длительность 25 лет.
5. Нулевой купон, длительность 5 лет.
6. Нулевой купон, длительность 25 лет.

Изобразив зависимость цена – доходность для любой облигации без встроенных опционов графически, мы получим кривую, приведенную на рис. 4.1. Заметим, что при росте требуемой доходности цена облигации без встроенных опционов падает. Это соотношение, однако, не линейно (его график не является прямой линией). Кривую, представляющую зависимость цена – доходность для любой облигации без встроенных опционов, принято называть выпуклой.

Зависимости цена – доходность, описываемые здесь, связаны с мгновенными изменениями требуемой доходности. Напомним (подробнее об этом см. главу 2), что изменения цены с течением времени являются также следствием: 1) изменения представлений о кредитном качестве эмитента, 2) приближения даты погашения (в случае облигации, купленной с дисконтом или премией) и 3) изменения рыночных процентных ставок.
ВОЛАТИЛЬНОСТЬ ЦЕНЫ ОБЛИГАЦИИ БЕЗ ВСТРОЕННЫХ ОПЦИОНОВ
В табл. 4.2 приведены значения процентного изменения цен на шесть гипотетических облигаций из табл. 4.1, связанного с изменениями требуемых доходностей (мы исходили из предположения о том, что начальная доходность всех облигаций составляла 9 %). Анализ данных табл. 4.2 позволяет сделать несколько выводов о свойствах волатильности цен на облигации без встроенных опционов.
Свойство 1: Цены всех облигаций без встроенных опционов движутся в направлении, противоположном направлению движения требуемой доходности, однако процентные изменения цен для разных облигаций разнятся.
Таблица 4.2. Мгновенные процентные изменения цен шести гипотетических облигаций
Шесть гипотетических облигаций, цена которых изначально соответствует доходности 9 %:
Купон 9 %, длительность 5 лет, цена = $100,0000 Купон 9 %, длительность 25 лет, цена = $100,0000 Купон 6 %, длительность 5 лет, цена = $88,1309 Купон 6 %, длительность 25 лет, цена = $70,3570 Купон 0 %, длительность 5 лет, цена = $64,3928 Купон 0 %, длительность 25 лет, цена = $11,0710

Свойство 2: При небольшом падении требуемой доходности цена (в процентном отношении) меняется так же, как и при небольшом росте требуемой доходности.
Свойство 3: Если требуемая доходность претерпевает заметные изменения, при ее росте цена (в процентном отношении) меняется не так, как при падении аналогичного размера.
Свойство 4: При сильном изменении требуемой доходности на данное количество базисных пунктов процентный рост цены больше, чем ее процентное падение.
Суть свойства 4 на практике сводится к следующему: если инвестор владеет облигацией (т. е. имеет длинную позицию по облигации), а требуемая доходность падает, то прибыль от облигации будет больше, чем убыток, который инвестор потерпит в случае роста требуемой доходности на то же число базисных пунктов. И наоборот: если инвестор открыл по облигации короткую позицию, потенциальный убыток при изменении требуемой доходности на данное число базисных пунктов окажется выше потенциальной прибыли.
Все четыре свойства волатильности цены могут быть объяснены, исходя из выпуклости зависимости цена – доходность. Более подробно данная тема будет рассмотрена в этой главе ниже.
Параметры облигации, определяющие волатильность ее цены
Волатильность цены облигации без встроенного опциона определяют два параметра: купон и длительность.
Параметр 1. При данной длительности и начальной доходности волатильность цены облигации тем выше, чем ниже купонная ставка. Доказательством этого положения может служить сравнение поведения цен облигаций с купоном 9 %, 6 % и 0 %, имеющих одинаковую длительность.
Параметр 2. При данной купонной ставке и начальной доходности, чем дольше срок до погашения, тем выше волатильность цены. Сравните приведенные в табл. 4.2 данные о ценах на пятилетнюю и 25-летнюю облигации с одинаковым купоном.
На практике второе положение может быть расшифровано следующим образом: инвестор, ожидающий падения процентных ставок и желающий нарастить волатильность стоимости портфеля, должен собрать в портфель облигации с более долгим сроком до погашения. В ситуации ожидаемого роста процентных ставок уменьшить волатильность цены портфеля можно, собрав в портфеле облигации с более короткими сроками до погашения.
Влияние на волатильность доходности к погашению
Не следует забывать, что соображения кредитного качества заставляют облигации, имеющие одинаковые купоны и длительности, торговаться с разными доходностями. Каким образом, при прочих равных, влияет на волатильность цены доходность к погашению? Анализ показывает: чем выше доходность к погашению, тем ниже волатильность цены.
В табл. 4.3 приведены данные о 25-летней облигации с 9 %-ным купоном, торгующейся с разными уровнями доходности. В первой колонке показан уровень доходности облигации, во второй – стартовая цена. Третья колонка показывает цену при изменении доходности на 100 базисных пунктов. Четвертая и пятая колонки демонстрируют долларовое и процентное изменение цены. Заметим, что чем выше начальный уровень доходности, тем ниже волатильность цены. Таким образом, при данном изменении доходностей волатильность цен выше на рынке, где уровни доходности низки, и наоборот: при высоких уровнях доходности волатильность невелика.

ИЗМЕРЕНИЕ ВОЛАТИЛЬНОСТИ ЦЕНЫ ОБЛИГАЦИИ
Управляющие портфелями, арбитражеры и трейдеры, которые хотят успешно применять разнообразные стратегии хеджирования и торговли, должны уметь измерять волатильность цены на облигацию. Существует три наиболее распространенных меры волатильности: 1) ценовая стоимость базисного пункта, 2) величина изменения доходности, соответствующая изменению цены, и 3) дюрация.
Ценовая стоимость базисного пункта
Ценовая стоимость базисного пункта, известная также как долларовая стоимость 01 (dollar value of 01), – это изменение цены облигации при изменении требуемой доходности на один базисный пункт. Обратите внимание на то, что данная мера волатильности описывает долларовую волатильность цены, в отличие от волатильности процентной (изменение цены как процент от стартовой цены). Как правило, ценовая стоимость базисного пункта выражается в виде абсолютной величины изменения цены. Напомним, что, согласно свойству 2 взаимосвязи цена – доходность, волатильность при росте требуемой доходности на 1 базисный пункт равна волатильности при аналогичном падении требуемой доходности.
Вычисление ценовой стоимости базисного пункта мы продемонстрируем на примере шести облигаций, описанных нами в табл. 4.1. Для каждой облигации приведены значения стартовой цены, цены после увеличения требуемой доходности на 1 базисный пункт (с 9 % до 9,01 %) и ценовая стоимость базисного пункта (разность между двумя ценами).

Данная мера волатильности цены отражает изменение цены в долларах. Деление ценовой стоимости базисного пункта на стартовую цену даст значение процентного изменения цены при изменении доходности на 1 базисный пункт.
Величина изменения доходности, соответствующая изменению цены
Другая мера волатильности цены облигации, используемая инвесторами, – это величина изменения доходности, соответствующая определенному изменению цены. Для ее вычисления прежде всего подсчитывают доходность к погашению облигации при падении цены облигации на Х долларов. Затем находится разность между начальной доходностью и новой доходностью, т. е. изменение доходности, соответствующее изменению цены на Х долларов. Чем меньше данная величина, тем выше долларовая волатильность цены, поскольку для изменения цены на Х долларов достаточно будет меньшего изменения доходности.
До недавнего времени казначейские ноты и облигации котировались на основе 1/32 процентного пункта. Таким образом, инвесторы рынка казначейских ценных бумаг вычисляли изменение доходности, соответствующее изменению цены на 1/32. Наши две гипотетические облигации с купоном 9 % при условии падения цены на 1/32 демонстрируют следующее изменение доходности:

Корпоративные и муниципальные облигации, речь о которых пойдет в главах 6 и 7, торгуются с минимальным изменением цены, равным 1/8 процентного пункта. Таким образом, инвесторы этих рынков вычисляют изменение доходности, соответствующее изменению доходности на 1/8. Две гипотетические облигации с купоном 9 % при условии падения цены на 1/8 демонстрируют следующие доходности:

