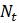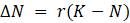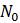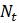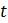Математические модели в естественнонаучном образовании. Том I

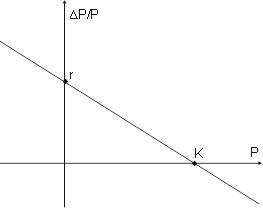
Рисунок 1.1. Темпы роста численности

 в зависимости от текущего значения численности .

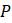
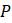
Конечно, нельзя предугадать, как выглядит график

 без сбора дополнительной информации. Возможно, график должен быть вогнутым или выпуклым, например. Тем не менее, это лишь первая попытка создать новую модель.

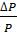
Вопросы для самопроверки:

– Постройте график темпов роста значений численности по мальтузианской модели. Чем тот график отличается от изображенного на рисунке 1.1?

Для мальтузианской модели

, поэтому тот график темпов роста представляет собой горизонтальную линию и снижения  по мере увеличения  не происходит. С другой стороны, наклонная линия рисунка 1.1 улучшенной модели приводит к формуле , для некоторых  и . В конечном итоге закономерность проявится яснее если записать уравнение прямой как  , где  – абсцисса точки пересечения горизонтальный оси,  – ордината пересечения вертикальной. Заметим, что   и  должны быть положительными. Через алгебраические выкладки получим новое разностное уравнение . Эта модель обычно называется «дискретной логистической моделью» или «дискретным логистическим уравнением», хотя, к сожалению, многие модели называются также.

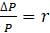
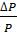
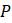
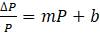
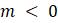
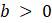
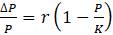
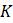
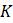
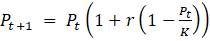
Параметры

 и  в этой модели имеют физические и биологические интерпретации. Во-первых, если , то . При положительных темпах роста на душу населения население будет увеличиваться. С другой стороны, если , то . При отрицательных темпах роста на душу населения численность населения будет сокращаться.  Поэтому  называют несущей способностью окружающей среды, потому что она представляет собой максимальное количество особей, которые могут поддерживаться в течение длительного периода. Однако, когда население незначительно (т.е.  намного меньше, чем ), множитель  устремляется в 1. Поэтому для малых значений  модель аппроксимируется приближенными значениями .

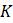
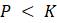
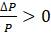
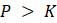
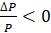
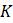
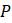
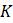
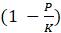
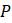
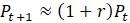
Другими словами,

 играет роль , в вышеописанной линейной модели. Параметр  просто отражает то, как популяция будет расти или уменьшаться в отсутствие факторов, зависящих от плотности, когда численность намного ниже предельного значения. Как правило  называют конечной внутренней скоростью роста. Термин «внутренний» относится к отсутствию внешнего воздействия, зависящего от плотности, а термин «конечный» подчеркивает тот факту, что используются временные шаги конечного размера, а не бесконечно малые временные шаги дифференциального уравнения.

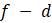
Вопросы для самопроверки:

– Какие значения можно ожидать от

 и  в случае, когда захотите смоделировать численность ежегодно поступающих на физико-математические факультеты омских ВУЗов?

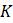
Как вы увидите в задачах ниже, существует много способов, которыми разные авторы формируют логистические модели, в зависимости от того, смотрят ли на

 или , используют ли различные множители. Ключевым моментом, который поможет распознать нелинейную модель, является то, что и , и  выражаются как квадратные трехчлены от . Кроме того, эти многочлены не имеют свободного члена (т.е. члена нулевой степени). Таким образом, логистическая модель является простейшей нелинейной моделью, которую можно придумать. Как и в случае с линейной моделью, первым шагом в понимании этой модели является выбор некоторых конкретных значений для параметров  и , а также для начальной численности  и вычисление следующих значений . Например, выбирая  и  так, что  и , получаем таблицу 1.5.

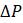
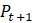
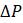
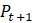
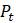
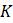
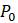
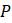
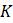
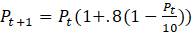
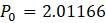
Таблица 1.5. Популяционные значения из нелинейной модели

t             0             1             2             3             4             5             6             7             8             9             10

           2.0117  3.2972  5.0653  7.0650  8.7238  9.6145  9.9110  9.9816  9.9963  9.9993               9.9999

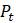
Вопросы для самопроверки:

– Какой смысл могут иметь популяции, значения которых не являются целыми числами?

Если измерять размер популяции в единицах, таких как тысячи или миллионы особей, то нет никаких оснований для того, чтобы популяции были целыми числами. Для некоторых видов, таких как коммерчески ценные рыбы, может быть даже целесообразно использовать единицы массы или веса, такие как тонны.

Другая причина, по которой нецелочисленные значения популяции не вызывают опасения, даже если используем поштучные единицы измерения, заключается в том, что пытаемся лишь приблизительно описать размер популяции. Нет ожидания того, что модель даст точные прогнозы. Пока числа невелики, можно просто игнорировать дробные части без значительных потерь.

В таблице 1.5 видим, что популяционное значение увеличивается до пропускной способности 10, как и ожидалось. Сначала это увеличение кажется медленным, затем оно ускоряется, а затем снова замедляется. Построение значений популяции на рисунке 1.2 показывает сигмовидную картину, которая часто появляется в данных тщательно контролируемых лабораторных экспериментов, в которых популяции увеличиваются в ограниченной среде. График показывает значения популяции, связанные сегментами линий, чтобы сделать шаблон более ясным, хотя дискретные временные шаги нашей модели действительно дают популяции только в целочисленное время. Таким образом, с интуитивной точки зрения мы добились определенного прогресса; у нас есть более реалистичная модель для описания роста населения или численности выпускников физико-математических специальностей.

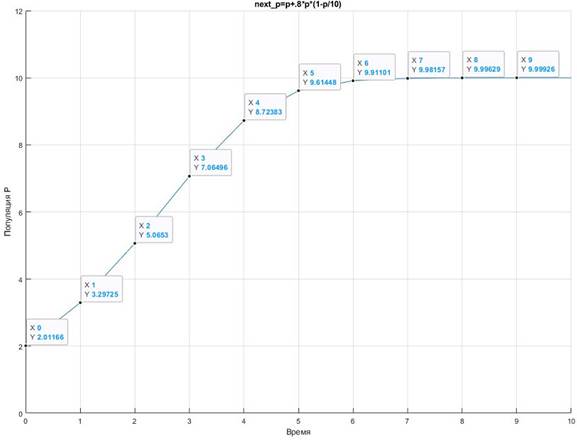
Рисунок 1.2. Популяционные значения из нелинейной модели.

Однако с математической точки зрения не всё так хорошо. В отличие от линейной модели, нет очевидной формулы для

, которая возникала бы из составленной таблицы. На самом деле, единственный способ получить значение , по-видимому, заключается в создании таблицы с сотней записей в ней. Утратилась легкость, с которой можно было бы предсказывать будущие значения популяции.

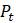
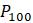
Это то, с чем приходится мириться: хотя нелинейные модели более реалистичны, зачастую не представляется возможным получение явных формул для решения нелинейных дифференциальных уравнениях. Вместо этого используются графические методы и численные эксперименты для того, чтобы получить общее представление о поведении модели.

Первый из таких методов называется «Паутина». Паутина является основным графическим методом для понимания математической модели дискретного логистического уравнения. Это лучше всего проиллюстрировать на примере.

Рассмотрим еще раз модель

, . Начнём с построения графика параболы, определенной уравнением, выражающим  через , а также диагональной линии , как показано на рисунке 1.3. Так как популяция начинается с , отмечаем это значение на горизонтальной оси графика. Теперь, чтобы найти , просто двигаемся вертикально вверх по графику параболы, чтобы найти точку , как показано на рисунке.

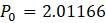
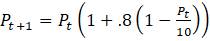
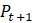
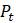
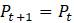
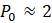
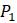
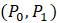
Далее хотелось бы найти

, но для этого нужно отметить  на горизонтальной оси. Самый простой способ сделать это – двигаться горизонтально от точки  до диагональной линии. Когда достигнем диагональной линии, окажемся в , так как сохранили ту же вторую координату, но изменили первую координату. Теперь, чтобы найти , просто двигаемся вертикально назад к параболе, чтобы найти точку . Теперь это просто вопрос повторения этих шагов навсегда: двигаться вертикально к параболе, затем горизонтально к диагональной линии, затем вертикально к параболе, затем горизонтально к диагональной линии и так далее.

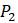
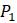
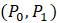
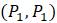
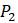
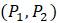
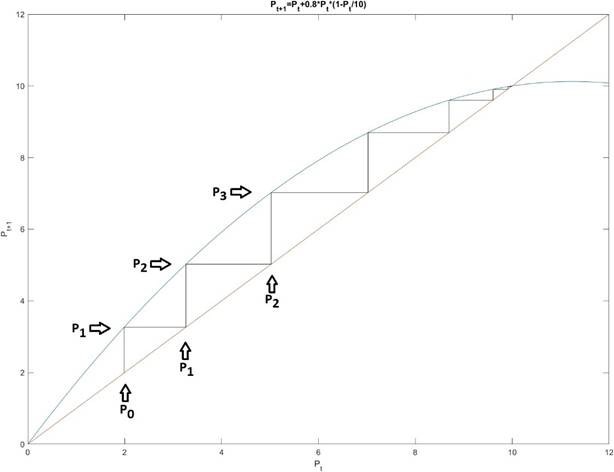
Рисунок 1.3. Паутинная диаграмма нелинейной модели.

Судя по графику ясно, что если начальная популяция

 лежит в диапазоне от 0 до , то модель с  и  приведёт к постоянно растущему значению популяции, которое приближается к предельному значению пропускной способности равному 10.

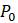
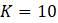
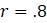
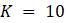
Если оставить те же значения

 и , но положить , то паутина будет выглядеть так, как показано на рисунке 1.4.

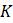
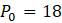
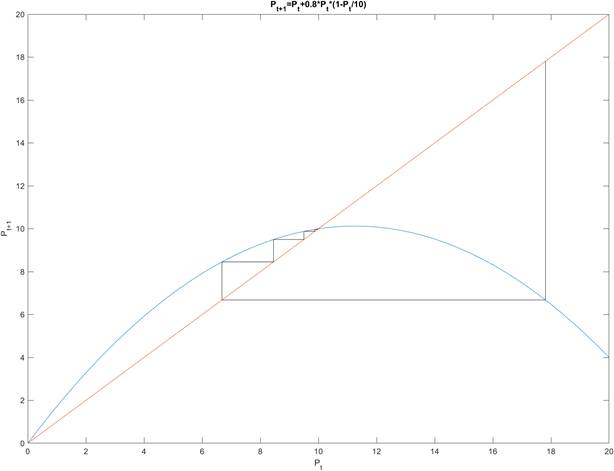
Рисунок 1.4. Паутинная диаграмма нелинейной модели.

Действительно, становится ясным, что если

 имеет значение больше, чем , то наблюдается немедленное падение численности популяции. Если такое падение окажется ниже критического, то произойдёт постепенное увеличение, приближающееся обратно к предельному значению пропускной способности модели.

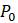
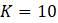
Вопросы для самопроверки:

– Для модели

 найдите отличное от нуля значение , соответствующее абсциссе точки пересечения параболы с горизонтальной осью, то есть имеющей ординату .

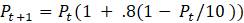
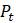
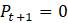
– Что произойдет, если

 выбрать больше, чем значение, найденное в предыдущем вопросе?

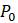
Если популяция становится отрицательной, то мы должны интерпретировать это как вымирание.

На этом этапе можно узнать гораздо больше, изучая логистическую модель с помощью калькулятора или компьютера, чем просто прочитав текст. Упражнения ниже помогут в этом. На самом деле обнаружится, что логистическая модель имеет некоторые сюрпризы, которые вы, возможно, не ожидаете.

Задачи для самостоятельного решения:

1.2.1. Пусть

 и . С помощью калькулятора составьте таблицу популяционных значений  для . Изобразите полученные результаты на графике.

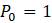
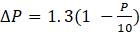
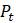
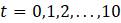
1.2.2. В модели

, какие значения  приведут к тому, что  окажется положительным? Отрицательным? Какой смысл это имеет?

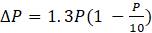
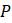
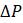
1.2.3. Повторите решение задачи 1 в MATLAB с помощью команд аналогичных следующим:

p=1; x=p

for i=1:22; p=p+.3*p*(1-p/15); x=[x p]; end

plot([0:22], x)

Объясните, как это работает.

1.2.4. Используя следующую программу onepop.m для MATLAB при различных значениях

, исследуйте долгосрочное поведение модели , где . Возможно, придется изменить количество шагов, с которыми вы запускаете модель, чтобы изучить некоторые из вариантов.

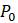
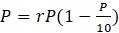
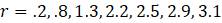
% onepop.m

%

% Модель популяции одного вида

%

% У пользователя запрашивается уравнение, определяющее модель. Затем, кликнув

% по начальной численности популяции на графике, динамика популяции как функция

% от времени будет изображена в виде графика. После выполнения симуляции

% при нажатии клавиши 'd' числовые данные отобразятся в командное окно MATLAB.

%

p=0;                          % инициализация переменной популяции для формулы

%

disp(' ')

disp(' Введите формулу, определяющую модель популяции, обозначая за "p"')

disp('численность популяции: (Например: следующее_p = p+.8*p*(1-p/10) )')

next_p=input ('следующее_p = ','s');

%

p=eval(next_p);               % тестируемая формула

%

disp(' ')

disp(' Введите диапазон популяции, который будет отображаться на графике:');

limits=input('(Значение по умолчанию [pmin pmax] = [0 20]) ');

if isempty(limits) limits=[0 20]; end;

%

disp(' ')

n=input(' Введите количество шагов для итерации: (по умолчанию n = 20) ');

if isempty(n) n=20; end;

%

disp(' ')

disp(' Наведите курсор на график, чтобы выбрать начальную популяцию и')

disp('кликните для рисования. Нажмите `d'', чтобы отобразить значения популяции')

disp('в командном окне. Нажмите любую другую клавишу, чтобы выйти.')

disp('  ')

disp(' Нажмите любую клавишу, чтобы начать.')

pause

%

figure;                         % настроить отображение нового графика

axis([ [0 n] limits]); grid on;

xlabel('Время');ylabel('Популяция P');

title(['следующее\_p=',next_p]);

hold on;                        % сохранение линий на графике при добавлении новых

%

times=[0:n];                    % генерировать вектор времени для построения графика

%

newcontinue=1;

while newcontinue               % цикл, пока не будет нажата не левая кнопка

   [t,p,button]=ginput(1);      % получить начальную численность популяции

   if button==1

      pops=p;

      for i=1:n                 % построить вектор итерационных значений популяции

         p=eval(next_p);

         pops=[pops,p];

      end

      plot(times,pops);         % график зависимости численности популяции от времени

   else

      newcontinue=0;            % флаг выхода из цикла

      if button==100

         [times;pops]'          % отобразить время и численность в командном окне

         newcontinue=1;           % повторить цикл снова после отображения значений

                                % если пользователь нажимает `d' для отображения

      end

   end

end

%

hold off                        % возвращает режим автоматической очистки графика

1.2.5. Наиболее распространенными способами записи уравнения дискретного логистического роста являются:

, , , .

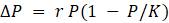
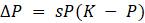
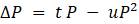
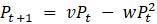
Представьте каждую из следующих моделей в четырех основных формах записи.

а.

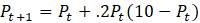
б.

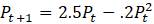
1.2.6. Дано уравнение модели

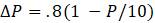
а. Постройте график функции

 от  с использованием MATLAB путем ввода команды:

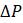
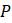
x=[0:.1:12]

y=.8*x.*(1-x/10)

plot(x,y)

б. Постройте график функции

 от  путем изменения команд MATLAB из части (а).

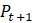
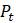
в. Вычислите значения

 для  при . Затем на графике из части (б) постройте паутину, начинающуюся с . Можно добавить линию  на графике, введя команды

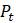
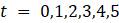
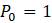
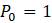
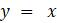
hold on, plot(x,y,x,x)

Полученная паутинная диаграмма достаточно точно соответствует таблице значений?

1.2.7. Если бы данные в таблице 1.6 о численности популяции были собраны в ходе лабораторного эксперимента, описывались бы они хотя бы приблизительно логистической моделью? Объясните почему. Если данные описываются логистической моделью, то можете ли оценить

 и  в модели ?

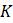
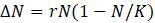
Таблица 1.6. Значения численности популяции

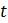
0 1             2             3             4             5             6             7             8             9             10

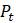
           1,94       3,04       4,62       6,72       9,26       11,88     14,08     15,52     16,26     16,60     16,72

1.2.8. Предположим, что популяция моделируется уравнением

 когда  измеряется поштучно.

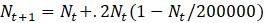
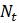
а. Найдите уравнение той же формы, описывающее ту же модель, но с популяцией, измеряемой в тысячах штук. Подсказка: пусть

, тогда  и можно найти формулу для описания зависимости  от .

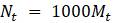
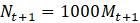
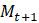
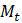
б. Найдите уравнение той же формы, описывающее ту же модель, но для популяции, измеряемой в единицах, выбранных таким образом, чтобы пропускная способность составляла 1 в этих единицах. Для начала определите пропускную способность исходной модели.

1.2.9. Метод построения паутинной диаграммы для изучения итерированных моделей не ограничивается только моделированием логистического роста, описанного выше. Определите графически популяции в каждой из моделей на рисунке 1.5 выполнив шесть итераций приращения, используя отмеченные начальные значения численности популяции

.

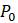
а.

б.

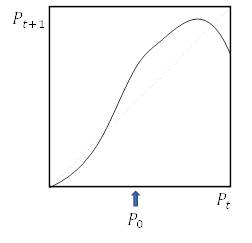
в.

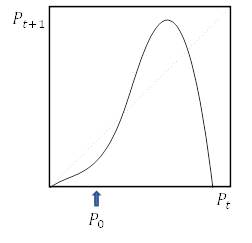
г.

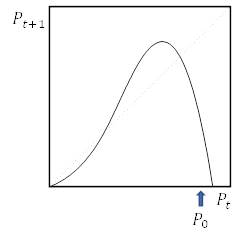
Рисунок 1.5. Паутинные диаграммы для задачи 1.2.9.

1.2.10. Приведите формулу для графика, изображенного в части (а) рисунка 1.5. Как называется такая модель?

1.2.11. Некоторые из одних и тех же идей и моделей, используемых в исследованиях популяций, появляются в совершенно неожиданных научных областях.

a. Часто химические реакции протекают со скоростью, пропорциональной количеству участвующего в реакции вещества. Предположим, что используется очень малый временной интервал, чтобы смоделировать такое действие разностным уравнением. Пусть общее количество химических веществ участвующих в реакции равно

, и то первое химическое вещество, которое изначально имеется в количестве , преобразуется во второе химическое вещество, которое получается в количестве  в момент времени . Опираясь на свои школьные знания, объясните, почему . Какие значения  являются допустимыми? Какой смысл имеет ? Как выглядит график функции  от ?