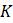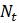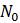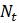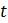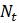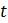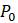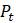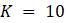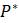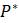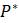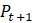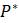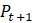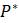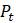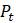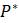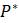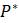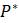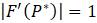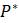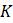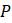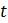b. Химические реакции называются автокаталитическими, если скорость, с которой они происходят, пропорциональна как количеству сырья, так и количеству продукта, тот есть продукт реакции отказывается её катализатором. Модно снова использовать очень малый интервал времени для моделирования такого действия, но уже с помощью другого уравнения. Пусть общее количество химических веществ участвующих в реакции равно
и то одно химическое вещество преобразуется в другое химическое вещество, которое получается в количестве
? Можете ли интуитивно объяснить форму полученного графика? Обратите внимание на тот факт, что
будет очень маленьким, потому что используется небольшой интервал времени. Модель логистического роста в таких случаях иногда также называют автокаталитической моделью.
Заметим, что пришедшая из химии автокаталитическая модель применима, среди прочего, для моделирования динамики трудовой миграции в сфере математического образования.
1.3. Анализ нелинейных моделей
В отличие от простой линейной модели, описывающей экспоненциальный рост, нелинейные модели, такие как дискретная логистическая, могут описывать достаточно сложную динамику поведения. Без сомнения, это стало заметным в ходе выполнения некоторые упражнений из предыдущего раздела.
В этом разделе рассмотрим несколько конкретных типов поведения и разработаем простые инструменты для их изучения.
Начнём с моделирования таких явлений, как переходные процессы, равновесие и стабилизация. Полезно выделить несколько аспектов, связанных с поведением динамической модели. Иногда, несмотря на первоначальную уникальность, после того как прошло много шагов, поведение модели становится шаблонным. Первые несколько шагов итерации, однако, могут не указывать на то, что подобное произойдет в долгосрочной перспективе. Например, с дискретной логистической моделью
и большинство начальных значений , первые несколько итераций модели производят относительно большие изменения в по мере дальнейшего приближения к 10. Таким образом, подобное поведение на ранней стадии называется переходным, потому что оно в конечном итоге сменяется другим поведением. Однако это не означает, что переходные процессы не вызывают интереса, поскольку реальные популяции вполне могут переживать кризисные ситуации, которые продолжают возвращать популяцию обратно на переходный этап.Как правило, исследователей интересует долгосрочное поведение модели. Причина этого заключается в том, что изучаемая система не должна быть разрушена раньше, чем прекратятся переходные процессы. Часто, но далеко не всегда, долгосрочное поведение не зависит от точной численности исходной популяции. В модели
, долгосрочное поведение для большинства начальных значений заключается в том, что популяция становится очень близкой к . Заметим, что если , то , следовательно в дальнейшем численность популяции никогда не поменяется. Таким образом, является равновесием (или стационарной, фиксированной точкой) модели.Определение. Равновесным значением для модели
является значение такое, что . Это эквивалентно тому, что для модели существует значение такое, что .Нахождение равновесных значений сводится к решению уравнения равновесия. Для модели
, решив уравнение видим, что существует ровно два равновесных значения: и .Вопросы для самопроверки:
– Графически тоже можно найти равновесия, выполнив поиск пересечения кривой
с диагональной прямой. Почему это так?Тем не менее, Равновесие все еще может иметь различные качественные особенности. В примере выше
и являются равновесиями, но популяция, близкая к 0, имеет тенденцию отходить от 0, тогда как популяция близкая к 10 имеет тенденцию двигаться к 10. Таким образом, 0 является неустойчивым или отталкивающим равновесием, а 10 является стабильным или притягивающим равновесием.Предположим, что модель близка к описанию реальной популяции, стабильные равновесия – это те, которые можно наблюдать не только в живой природе. Поскольку любая система, вероятно, будет иметь небольшие отклонения от идеальной модели, даже когда популяция находится в состоянии равновесия, ожидается, что она будет меняться, по крайней мере, благодаря тем факторам, которые исключены из модели или изначально не принимались во внимание. Однако, отклоняясь на небольшое расстояние от стабильного равновесия, наблюдаемое значение будет возвращаться к нему обратно. С другой стороны, если происходит отклонение от неустойчивого равновесия, то наблюдаемое значение остается в стороне. Хотя нестабильные равновесия важны для понимания модели в целом, они не являются характерными особенностями популяции, которые стоит когда-либо ожидать в реальном мире.
Далее займёмся вопросами линеаризации. Следующая цель – определить, что заставляет одни равновесия быть стабильными, а другие – нестабильными.
Стабильность зависит от того, что происходит вблизи равновесия. Итак, чтобы сконцентрироваться в окрестности
, рассмотрим популяцию , где – очень маленькое число, которое говорит о том, насколько далеко популяция находится от состояния равновесия. Называется отклонением от равновесия и интересно тем, как оно меняется с течением времени. Вычислим и используем его для поиска . Если больше, чем по абсолютной величине, то можно сделать вывод о том, что отдалилось от . Если наоборот, меньше по абсолютной величине, то приблизилось к . Если теперь проанализировать, как меняется на всех достаточно малых значениях , то можно будет определить, является ли исследуемое равновесие стабильным или нестабильным. Растущее отклонение означает нестабильность, в то время как уменьшающееся означает стабилизацию. Здесь не учитывается знак отклонения, рассматривая лишь абсолютное значение. Знак стоит принимать во внимание в последнюю очередь, так как он не имеет прямого отношения к вопросу о стабильности.Пример. Рассмотрим модель
, с которой уже сталкивались ранее и знаем, что равновесие достигается в точках и 10. В первую очередь исследуем , которое, судя по графику, стабилен на основании численных экспериментов. Подстановка значений и в уравнение для модели приводит к следующему выводу:
Заметим, что
является очень малым числом, меньше 1, следовательно, еще меньше и ничтожно мало по сравнению с . Таким образом .Это означает, что значения
близкие к равновесию будут иметь отклонение от равновесия, уменьшающееся примерно в 0.3 раза с каждым последующим шагом времени. Поэтому небольшие отклонение от равновесия в дальнейшем уменьшаются и действительно стабильное значение.Можно смотреть на число 0.3 как на «коэффициент растяжения», который говорит о том, насколько стремительно меняются отклонения от равновесия с течением времени. В данном примере, поскольку растягиваемся в менее чем 1 раз, на деле имеет место сжатие.
Процесс, описанный в примере выше, называется линеаризацией модели в равновесии, потому что сначала фокусируем внимание вблизи равновесия путем линейной замены
, а затем игнорируем члены степени больше 1 в . Остается только линейная модель, аппроксимирующая исходную модель. Линейные модели, как видели, легко понять, потому что они производят либо экспоненциальный рост, либо распад.Вопросы для самопроверки:
– Выполните аналогичный анализ для другого равновесия этой модели, чтобы показать, что оно нестабильно. Каким будет коэффициент растяжения, на который расстояния от точки равновесия растут с каждым шагом времени?
В результате аналогичного анализа в окрестности 0 обнаружится, что линеаризация при
дает . Поэтому возмущения от этого равновесия со временем растут, следовательно, неустойчиво. В общем случае, когда коэффициент растяжения больше 1 по абсолютной величине, равновесие нестабильно. И наоборот, когда оно меньше 1 по абсолютной величине, равновесие стабильно.Из курса математического анализа известно, что вышеописанный процесс линеаризации напоминает аппроксимацию графика функции по касательной прямой. Развивая эту идею коэффициент растяжения в предыдущем примере можно было бы выразить как отношение
при бесконечно малых значениях . Но , где уравнение, определяющее модель. Заметим, что в последнем равносильном преобразовании использовалось равенство . Поскольку интересны лишь значения , очень близкие к , то последнее выражение очень близко к предельному значению . Но этот предел по определению является не чем иным, как производной , производной функции, определяющей модель. Итак, мы доказали следующую теорему.Теорема. Если модель
имеет равновесное значение , то подразумевает, что значение нестабильно, а при , будет стабильным значением. Если же , то этой информации недостаточно для определения стабильности и необходимо проводить дополнительное исследование.Пример. Пусть
, тогда . Вычислим . Следовательно, , поэтому стабильно.Обратите внимание, что в этом примере значение, которое нашли для
, оказалось точно таким же, как значение, которое нашли для «коэффициента растяжения» в примере выше, без использования инструментов дифференциального исчисления. Это, конечно, должно было произойти, потому что то, что привело к производной, изначально было более тщательным исследованием «методом пристального всматривания». Таким образом, производную можно интерпретировать как меру того, насколько быстро функция меняет свои значения.Поскольку использовался формализованный подход, то есть записывались формулы и уравнения, для иллюстрации тесной связи между понятиями производной и стабилизацией поведения модели, настоятельно рекомендуется решить задачи с 1.3.1 по 1.3.3 в конце раздела, чтобы представить обнаруженную связь графически.
Почему важны как графический, так и аналитический подходы к определению стабильности? Первый является наиболее интуитивным и делает основные идеи наиболее ясными. Что можно было наблюдать на примере. Но слабость такого подхода в том, что он действенен лишь для моделей, включающих простые алгебраические формулы. Если бы в уравнении модели присутствовали экспоненты или другие сложные функции, алгебраические средства оказались бессильны. Когда модель усложняется, математический анализ становится прекрасным подручным инструментом для профессионального исследователя.
При линеаризации для определения стабильности очень важно сосредоточиться на равновесии. Даже не пытайтесь определить является ли точка стабильным или нестабильным равновесием, пока не убедитесь в том, что это точка является равновесием в принципе. Последующий анализ предполагает, что точка
удовлетворяет равенству . Например, если бы попытались линеаризовать для в предыдущем примере, то не смогли бы ничего сделать, потому что 11 не является точкой равновесия.Наконец, также важно, что проведённый анализ стабильного и неустойчивого равновесия, был локальным, а не глобальным. Эта устоявшаяся терминология означает, что рассмотрели лишь то, что происходит в очень небольших окрестностях вокруг точки равновесия. Хотя устойчивое равновесие будет притягивать все близлежащие значения, это не означает, что значения расположенные далекого тоже должны стремиться именно к нему. Точно так же, как несмотря на то нестабильность равновесие, нельзя утверждать, что далёкие от него значения не будут к нему стремиться или не окажутся вовсе ему равными.
Далее рассмотрим такие явления в динамическом моделировании как колебания, бифуркации и хаос. В задаче 1.2.4 предыдущего раздела исследовалось динамическое поведение логистической модели
для K = 10 при множестве значений r. На самом деле, параметр в модели не очень важен; можно выбрать единицы, в которых измеряется численность популяции так, чтобы пропускная способность стала равна 1. Например, если пропускная способность составляет 10 000 штук, то можно использовать масштабную единицу равную 10 000, и тогда получится . Это наблюдение позволяет подробно сосредоточиться на том, как параметр влияет на поведение модели.Зафиксировав
, для любого значения логистическая модель имеет два равновесных значения, 0 и 1, так как это единственные значения , которые приводят к . Как увидите в ходе решения задач чуть позже, «коэффициент растяжения» при будет равен , а при равен . Поэтому всегда является неустойчивым равновесием для .Случай
гораздо интереснее. Во-первых, когда , что равносильно , модель имеет стабильное равновесие в точке . Формула показывает, что знак при этом никогда не изменится; хотя отклонение уменьшается, первоначально положительное отклонение остается положительным, а изначально отрицательное – отрицательным. Популяция просто движется к равновесию, никогда не превышая его.Далее, когда
увеличивается настолько, что , то и равновесие будет все еще стабильным. Однако, теперь видим, что так как , то знак будет чередоваться между положительным и отрицательным значением по мере увеличения . Таким образом, можно видеть колебательное поведение выше и ниже точки равновесия, поскольку отклонение от равновесного значения имеет чередование знака. Таким образом, популяция приближается к равновесию как затухающее колебание.Подумаем о том, почему такое колебание может произойти с точки зрения моделируемой популяции. Если
, мера скорости воспроизводства новых ленов популяции, достаточно велика, то популяция ниже пропускной способности окружающей среды может за один временной шаг своего развития временно вырасти настолько, что превысит пропускную способность. Как только численность превышает пропускную способность, популяция вымирает достаточно быстро, чтобы к следующему шагу она снова оказалась ниже пропускной способности окружающей среды. Но затем её численность снова вырастет настолько, чтобы превзойти критическое значение. Как будто популяция перенастраивается и адаптируется заново на каждом временном интервале.Если параметр
логистической модели окажется больше только что рассмотренных значений, то популяция не приблизится к равновесию. Когда , получится и поэтому ранее устойчивое равновесие становится неустойчивым. Таким образом, происходит резкое качественное изменение поведения численности популяции по мере дальнейшего увеличения параметра . Отсюда возникает интересный вопрос, каковы возможности модели с двумя неустойчивыми равновесиями и без устойчивых. Какое поведение тогда можно ожидать в долгосрочной перспективе?Компьютерный эксперимент показывает, что для значений
чуть больше 2 популяция попадает в 2-цикл, её численность бесконечно прыгает взад и вперед между значением выше 1 и значением ниже 1. По мере дальнейшего увеличения значения в 2-цикле меняются, но наличие 2-цикла сохраняется до тех пор, пока не достигнем другого значения , при котором происходит еще одно внезапное качественное изменение. На этот раз видим, что 2-цикл становится 4-циклом. Дальнейшее увеличение производит 8-циклы, затем 16-циклы и так далее.