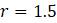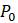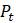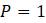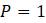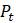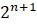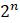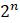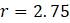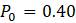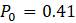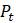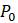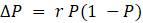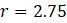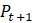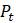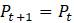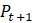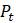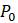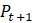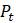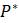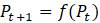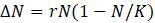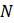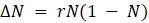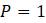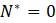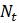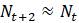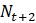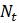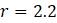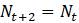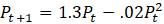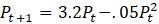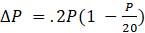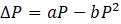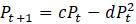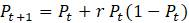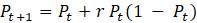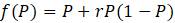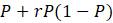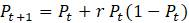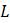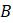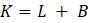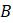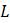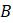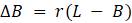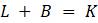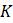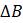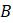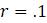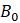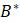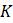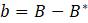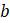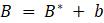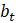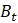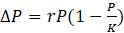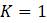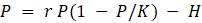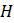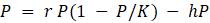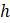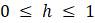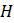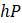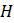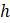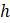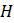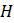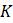Эта модель приводит к неожиданному, но интересному выводу: одна и та же популяция может демонстрировать разные циклы в своей численности, даже когда окружающая среда совершенно неизменна. Считая, что теоретические предположения в построении математической модели были верны и популяция имеет достаточно большое значение
, на практике она может никогда не достигать ни одного из теоретически существующих равновесных значений.
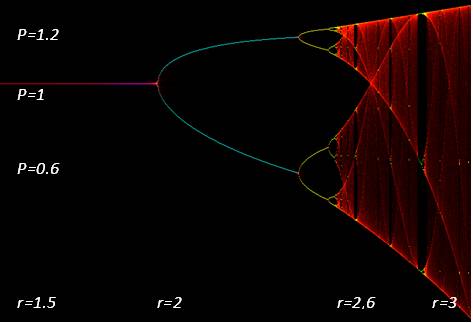
Хороший способ понять влияние изменения параметра
на рассматриваемую модель заключается в изображении диаграммы бифуркации на рисунке 1.6. В Maple это изображение легко получить следующей серией команд:
with(IterativeMaps):with(ImageTools):
Logistic := Bifurcation([x], [x + r*x*(1 – x)], [0.99], 1.5, 3):
ArrayTools:-Dimensions(Logistic)
ColouringProcedures:-HueToRGB(Logistic):Embed(Logistic)
Рисунок 1.6. Бифуркационная диаграмма логистической модели
. По горизонтальной оси слева направо меняется значение параметра
, а по вертикальной снизу вверх отложены циклические аттракторы значений соответствующей популяции.
Рисунок 1.6 получен следующим образом. Для каждого значения
на горизонтальной оси выбирается некоторое значение
и выполняется итерация модели на несколько временных шагов, чтобы пройти этап переходного процесса, например, раз 200. На практике это означает повторение итераций столько раз, пока не надоест. Затем продолжаются итерации на серии дополнительных шагов, раз 100, но теперь все значения
наносятся на вертикальную ось над конкретным используемым
. Это значения будут концентрироваться вокруг своеобразных точек притяжения, формируя так называемые циклические аттракторы.
Чтобы проиллюстрировать процесс для дискретной логистической модели, положим
. Тогда, независимо от
, после первого набора большого числа итераций,
будет очень близок к стабильному равновесию
. Таким образом, когда строим следующий набор из многих итераций, просто многократно строим точки, которые будут выглядеть так, будто они находятся в
. На рисунке 1.6 точки фрагмента этой горизонтальной прямой выделены розовым цветом.
Если теперь продолжить процесс построения диаграммы при
чуть большем чем 2, то первый набор итераций устремляет значения
в 2-цикл, и затем, когда строится график на последующем наборе итераций, появляются точки, которые циклически перескакивают назад и вперед между двумя значениями, поэтому кажется, будто построили две точки. На рисунке 1.6 точки сформировавшихся в результате ветвей выделены синим.
На этой диаграмме заметно несколько особенностей. Во-первых, интервал значений
, через который получаем
-цикл, будет короче, чем для предыдущего
-цикла. Таким образом, как только
становится достаточно большим, небольшие дополнительные увеличения его значения имеют более радикальные последствия.
Во-вторых, если
продолжает увеличиваться после определенной точки (≈2.692…), на рисунке 1.6 этот фрагмент подсвечен красным, то все бифуркации на
-циклах произошедшие ранее начинают смешиваться, обнаруживается принципиально иной тип поведения аттракторов. Создается впечатление, что предельные значения модели изменяются более или менее случайным образом. Однако такое поведение, конечно, не случайно – существует полностью детерминированная формула, воспроизводящая его. Техническая терминология для описания того, что произошло, заключается в том, что поведение модели стало хаотичным. Выбор слова «хаос» для описания этого процесса, возможно, неудачен, поскольку вызывает ассоциацию с элементами случайности и изначальной путаницы, которых на самом деле нет. Тем не менее, данная математическая модель прекрасно находит себе практическое применение в современных цифровых криптосистемах и аналоговых системах радиоэлектронной борьбы, поскольку достаточно просто реализуется на аппаратном уровне.
Подобный «хаос» в действительности имеет довольно точное техническое определение, но не будем его приводить. Вместо этого просто неформально укажем на два требования, которые математики предъявляют к употреблению этого слова: 1) модель должна быть детерминированной, то есть в ней не может быть случайности; и 2) прогнозы модели чрезвычайно чувствительны к начальным условиям.
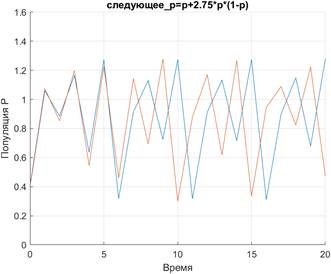
Чтобы увидеть, как именно дискретная логистическая модель проявляет свою хаотичность, например, зафиксировав
, достаточно проиллюстрировать проявление второго требования. На рисунке 1.7 показаны значения
, которые возникают из двух разных, но достаточно близких друг к другу значений
и
.
Рисунок 1.7 Результаты роста значения
, полученные из двух близких начальных значениях
для логистической модели
при
.
Обратите внимание на тот факт, что, хотя популяции и изменяются похожим образом в течение нескольких первых шагов, после этого они становятся полностью различимыми. В результате для такой пары значений наблюдается чрезвычайная чувствительность модели к начальным условиям. Конечно, это не является доказательством чего-либо, и вполне возможно, что такое поведение было просто последствием череды ошибок компьютерного округления. Однако математиками строго доказано, что это подлинный «хаос».
Возможность хаотического поведения в такой простой популяционной модели, как дискретная логистическая, вызвала большой ажиотаж в 1970-х годах, когда она была впервые опубликована в работе Мэй от 1978 года. Если бы такая простая модель смогла воспроизводить сложное поведение любой динамической системы, то от гипотезы о том, что сложная динамическая система может возникать лишь из сложных взаимодействий и флуктуаций окружающей среды пришлось бы отказаться. Дальнейшая работа Мэй с сотоварищами по вычислению соответствующих значений таких параметров, как

, в математических моделях на основании лабораторных и реальных популяциях насекомых заставила их усомниться в том, что хаотическое поведение действительно наблюдается в реальной динамике живых популяций. Тем не менее, исследование эпидемий кори в Нью-Йорке действительно предполагало возможность контролируемого хаоса. Однако эпидемический паротит и ветряная оспа, как оказалось, вели себя отнюдь не хаотично. Хотя та работа все еще не теряет актуальности, существует очень мало данных высокого качества и достаточно длительной продолжительности, чтобы в действительности проверить ключевую идею. В последнее время основное внимание уделялось демографическим моделям, более сложным, чем логистические. Фактически, в 1996 году Кушинг и др. объявили о первом открытии реальной популяции, лабораторной популяции мучного жука триболия, которая демонстрировала хаотическую динамику и опубликовали этот результат в 2001 году.
Задачи для самостоятельного решения:
1.3.1. Точки равновесия модели располагаются там, где график зависимости
от
пересекает прямую линию
. Предположим, что фокусируемся на участке графика вокруг точки равновесия и увеличиваем масштаб так, чтобы график функции
от
казался прямой линией. В каждой из моделей, показанных на рисунке 1.8, решите, является ли равновесие стабильным или нестабильным, выбрав значение
близкое к устойчивому состоянию, а затем изобразите паутинную диаграмму.
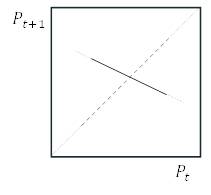
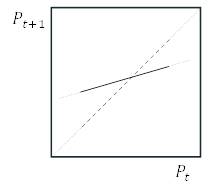
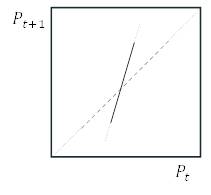
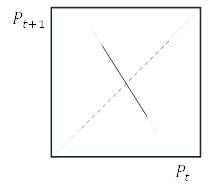
а.
б.
в.
г.
Рисунок 1.8. Заготовки паутинных диаграмм для задачи 1.3.1.
1.3.2. Исходя из приведенной выше задачи, в каком диапазоне должен находиться наклон графика функции
от
в точке равновесия, чтобы обеспечить стабильность? Неустойчивость? Подсказка: возможно, захотите подумать об особых случаях, взяв наклон сначала −1, а затем 1.
1.3.3. Средствами математического анализа сформулируйте ответ на предыдущую задачу на языке производных: если
является точкой равновесия модели
, то она стабильна, когда выполнено следующее условие _________________ .
1.3.4. С точки зрения математики, имея дело с логистической моделью роста
, всегда можно выбрать единицы, в которых измеряется
так, чтобы
.Таким образом, можно рассматривать уравнение
, имеющее только один параметр
, а не два. Исследуйте долгосрочное поведение этой модели для различных значений
, начиная с .5 и постепенно увеличивая его, используя программу onepop.m для MATLAB из задачи 1.2.4. При каких значениях
обнаруживается сходимость к равновесию без колебаний? А при каких
сходимость к равновесию осуществляется с колебаниями? При каких
появляется 2-цикл? А при каких – цикл длины 4?
1.3.5. В предыдущем упражнении обнаружили, что по мере увеличения
после значения 2 популяция перестанет стремиться к
и вместо этого попадет в цикл длины 2 и более.
а. Покажите, что, несмотря на срыв модели в 2-цикл, единственными точками равновесия по-прежнему являются
и 1.
б. Если
попадает в 2-цикл, то
. Поэтому, возможно, стоит найти формулу для
выраженного через
. Сделайте это для
и
. Ответ должен оказаться многочленом четвертой степени.
в. Можно ли использовать полученные результаты из части (б) для поиска аналитических формул точек равновесия в 2-цикле, приравняв
? Попробуйте. Не всё может получиться с первого раза, но, по крайней мере, попробуйте объяснить те сложности, с которыми столкнулись.
1.3.6. Для каждого из следующих пунктов определите точки равновесия.
а.
б.
в.
г.
д.
1.3.7. Для пунктов (а–д) из предыдущей задачи алгебраическими преобразованиями линеаризуйте модель сначала на устойчивом состоянии 0, а затем на другом устойчивом состоянии для определения типа их устойчивости.
1.3.8. Вычислите все точки равновесия модели
. Затем используйте чисто алгебраические средства для линеаризации в каждой из этих точек, чтобы определить, когда они стабильны или нестабильны.
1.3.9. Средствами математического анализа повторите решение предыдущей задачи используя производные для определения устойчивости равновесий
. Конечно, должны получиться те же ответы.
1.3.10. Несколько иной подход к поиску соотношения между производными и стабильностью заключается в следующем: найдите приближение касательной прямой к
в точках равновесия
и
. После этого замените
найденными линейными приближениями в уравнении
. Используйте это для определения типа стабильности точек равновесия. Полученный результат должен совпадать с ответами из двух предыдущих задач.
1.3.11. Моделирование многих социальных процессов связано с диффузией. Даже на уровне математических идей их взаимное проникновение между самыми разными отраслями очень заметно. Простым примером является найм выпускников математических специальностей на работу программистами (верно и обратное, квалифицированные программисты как правило дополнительно получают качественную математическую подготовку). Простая модель представляет социальную группу программистов как единый пул с концентрацией незаурядных умов
, а группу профессиональных математиков как смежный отдел с концентрацией умов
. Если для простоты предположить, что оба интеллектуальных пула имеют единичный объем, то в течение фиксированного промежутка времени на одной итерации найма новых сотрудников общее количество сотрудников
окажется неизменным. Если представить себе очень маленький фиксированный интервал времени, то увеличение
за этот временной интервал будет пропорционально разности между
и
. То есть
. Этот экспериментальный факт иногда называют законом Фика.
а. В каком диапазоне должен быть параметр
, чтобы эта модель имела смысл?
б. Используя тот факт, что
, формализуйте модель так, оставив лишь два параметра,
и
, чтобы выразить
через
.
в. Для
,
, и различных вариантов значений
, исследуйте модель с помощью программы onepop.m для MATLAB из задачи 1.2.4. Как изменится поведение модели, если использовать другое значение
?
г. Алгебраическим путём найдите точку равновесия
(выразив её через
и
) для этой модели. Согласуется ли это с тем, что вы видели в части (в)? Можете ли объяснить результат интуитивно?
д. Пусть
. Перепишите модель в виде зависимости от
, отклонения значений от точки равновесия, путем подстановки в
и дальнейшего упрощения полученного выражения.
е. Используйте часть (д), чтобы найти формулу для
, а затем для
. Убедитесь в том, что формула дает те же результаты, что и машинный эксперимент в onepop.m.
ж. Можно ли модифицировать модель так, чтобы описывалась диффузия между двумя отсеками разных размеров?
Проектные работы:
1. Предположим, что численность выпускников математических факультетов, трудоустраивающихся по специальности, имеет динамику, хорошо моделируемую дискретным разностным уравнением
.
Конечно, динамика этой численности всегда будет зависеть от значения
, но, выбрав соответствующие единицы измерения, можно зафиксировать
. Исследуйте влияние регулярного сокращения таких сотрудников при двух различных типах предположений.
а.
, где
– некоторое фиксированное число сотрудников, сокращаемых на каждом этапе времени, например, ежегодно.
б.
, где
– некоторый фиксированный процент сотрудников, сокращаемых на каждом временном этапе (
).
Рекомендации
Чтобы почувствовать модели, исследуйте тему с помощью onepop.m из задачи 1.2.4 для множества разумных вариантов параметров. Опишите любое необычное поведение модели и попытайтесь его объяснить.
Рассчитайте аналитически равновесия (которые могут быть выражены через
и
или
) и стабильность этих равновесий (которые также могут зависеть от
и
или
).
Объясните равновесие и стабильность с точки зрения паутинных диаграмм. Какое влияние оказывает вычитание
и
на паутинную диаграмму логистической модели?
Постарайтесь найти наибольшее
или
которое можно выбрать так, чтобы все еще было устойчивое равновесие. Если
или
выбраны как можно большими, чтобы все еще существовало стабильное равновесие (это вполне может быть экономически обоснованным), что произойдет с нестабильным равновесием?
Если бы вы отвечали за управление моделируемой организации, было бы вам комфортно, если бы стабильное равновесие находилось близко к нестабильному?
Существуют ли значения
, для которых
может быть больше
? Имеет ли это какой-либо смысл?
Если без проведения сокращений численность сотрудников не имеет устойчивого равновесия, то может ли принудительное сокращение привести к стабильности? Имеет ли это экономический смысл?
Используйте программу longterm.m для создания диаграмм, показывающих изменения моделируемой численности в долгосрочной перспективе по мере изменения параметров модели.
% longterm.m
fun = @(x,r) x + r*x*(1-x);
x0 = .99; a0 = 0; a1 = 3; N = 777; preL = 200; L = 100;
mat = bifur(fun,x0,a0,a1,N,preL,L);
function mat = bifur(fun,x0,a0,a1,N,preL,L,p_siz)
% –
% Функция bifur: строит однопараметрическую диаграмму бифуркаций
% Вход: fun = некоторая функция @(x,para)
% x0 = стартовое значение для x
% a0 = начальное значение параметра a
% a1 = конечное значение параметра a
% N = количество интервалов для параметра 'a' на отрезке [a0;a1]
% preL = количество предварительно пропускаемых итераций для
% преодоления переходного процесса перед стабилизацией
% L = количество итераций для каждой начальной пары
% от (x0,параметр a)
% p_siz = размер маркера, по умолчанию 1