
Макрокинетика сушки
Макроперенос количества движения происходит, например, при осаждении крупных частиц в турбулентном режиме за счет образования турбулентных завихрений. Движение частицы в этом случае описывается законом Ньютона.
При макропереносе имеет место также и микроперенос, однако интенсивность последнего намного ниже. При движении среды макроперенос, как правило, превалирует по сравнению с микропереносом. Именно поэтому макрокинетика наиболее важна, как определяющая все виды процессов переноса – переноса массы, энергии и количества движения или импульса.
1.5 Перенос массы
Рассмотрим поток вещества J в пространстве (Рис. 1.3). Концентрация вещества С изменяется в пространстве и во времени т. е.
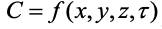
Вектор потока вещества между двумя изотермическими поверхностями, расположенными на бесконечно малом расстоянии dn друг от друга перпендикулярен к поверхности в любой точке [6].
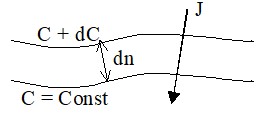
Рис. 1.3 Поток вещества в пространстве.
Поток вещества J, отнесенный к единице поверхности S в этом случае будет пропорционален градиенту концентрации:

Это выражение называется 1-м законом Фика. Здесь D – коэффициент диффузии.
Закон молекулярного переноса массы (вещества) для элементарного объема может быть получен следующим образом. Рассмотрим поток вещества через грани элементарного объема.
Расход вещества, обусловленный диффузией вдоль оси х через левую поверхность dy·dz (Рис. 1.4), с учетом закона Фика, составит.
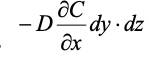
На расстоянии dx, с учетом изменения концентрации, получим ее значение

.
Тогда расход вещества, обусловленный диффузией вдоль оси х через правую грань dy·dz, составит
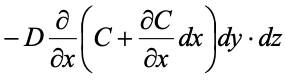
Таким образом, за счет изменения концентрации вдоль оси х в элементарный объем поступит количество вещества.
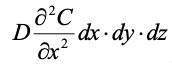
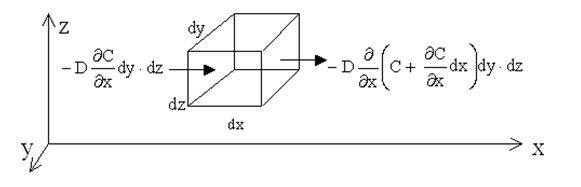
Рис. 1.4 К выводу 2-го закона Фика.
Аналогично определяется изменение количество вещества вдоль остальных осей. Суммарное изменение количество вещества, в пересчете на единицу объема, вдоль всех координат должно быть равно изменению его концентрации во времени:
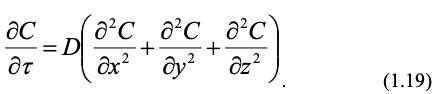
Выражение в скобках в уравнении (1.19) является оператором Лапласа. С учетом его сокращенного обозначения и образования вещества за счет химической реакции при скорости образования r получим для выражения (1.19):
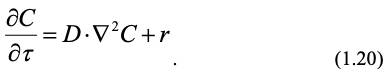
Уравнение (1.20) является следствием закона сохранения массы и 1-го закона Фика и называется 2-м законом Фика. Оно определяет поле концентраций для молекулярной диффузии в рассматриваемой среде.
Для изотропной диффузии уравнение (1.20) может быть записано для изменения вдоль любой оси, например х, в следующем виде:

При переносе массы в движущейся среде имеет место конвективный перенос и перенос за счет молекулярной диффузии. Тогда вместо частной производной концентрации по времени в уравнении (1.20) надо писать полную производную, учитывающую и конвективный перенос. С учетом этого для (1.20) получим:
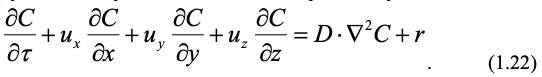
Уравнение (1.22) определяет поле концентраций с учетом молекулярной и конвективной диффузии. Как следует из этого уравнения, для описания макрокинетики процесса переноса массы необходимо учитывать гидродинамику и поэтому уравнение переноса в движущейся среде (1.22) должно быть дополнено уравнениями движения Навье-Стокса (1.10), определяющими поле скоростей и перенос импульса в движущейся среде.
Необходимо также отметить, что приведенные в данном разделе уравнения применимы для изотермической конвективной и молекулярной диффузии. Влияние изменения температуры описывается при молекулярном и конвективном переносе тепла.
1.6 Перенос тепла
Рассмотрим молекулярный перенос тепла аналогично переносу массы (Рис. 1.3). Температура t в общем случае изменяется как в пространстве, так и во времени т. е.
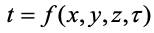
Тогда поток тепла q, отнесенный к единице поверхности S будет пропорционален градиенту температуры в произвольном направлении n:

Это выражение называется законом теплопроводности Фурье. Здесь – коэффициент теплопроводности среды.
Закон молекулярного переноса теплоты для элементарного объема может быть получен аналогичным образом, как и для переноса массы. Тогда суммарное изменение количества тепла вдоль всех 3-х координат элементарного объема, проявляющееся в изменении температуры, равно изменению температуры, вовремя помноженному на произведение теплоемкости ср на плотность ρ [6]:
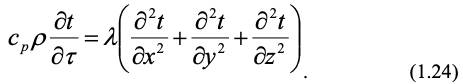
Выражение в скобках в уравнении (1.24) является оператором Лапласа, с учетом его сокращенного обозначения и дополнительного источника тепла qr, например, за счет химической реакции, с введением коэффициента температуропроводности а = / ср ρ, получим для выражения (1.24):
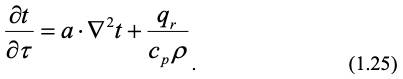
Уравнение (1.25) является следствием закона Фурье и также называется его именем. Оно определяет поле температур для молекулярного переноса тепла в рассматриваемой среде.
Для одномерной теплопроводности, например, вдоль оси х, уравнение (1.25) может быть записано в следующем виде:
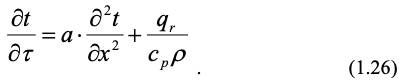
При переносе тепла в движущейся среде имеет место конвективный перенос и перенос за счет молекулярной диффузии. Тогда вместо частной производной температуры по времени в уравнении (1.25) надо писать полную производную, учитывающую и конвективный перенос. С учетом этого для (1.25) получим
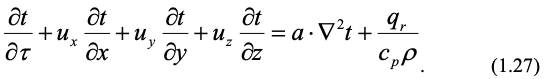
Уравнение (1.27) называется уравнением Фурье-Кирхгофа и определяет поле температур с учетом молекулярного и конвективного переноса тепла. Как следует из этого уравнения, для описания макрокинетики процесса теплопереноса необходимо учитывать гидродинамику и уравнение переноса в движущейся среде (1.27) должно быть дополнено уравнениями движения Навье-Стокса (1.10), определяющими поле скоростей в движущейся среде.
1.7 Перенос количества движения
По второму закону Ньютона изменение количества движения в единицу времени (импульс) численно равно силе – уравнение (1.8). В движущемся потоке газа или жидкости под действием массовых и поверхностных сил происходят соударения молекул, что обуславливает перенос количества движения. Баланс сил в движущемся потоке представляет собой закон сохранения количества движения (импульса). На основе баланса сил получена выше система уравнений Навье-Стокса (1.10).
Строго говоря, т. к. система уравнений Навье-Стокса получена на основе закона Ньютона для вязкостного трения (1.9), учитывающего молекулярный перенос количества движения (микроперенос), она применима только для струйчатого, ламинарного движения вязкой жидкости.
Если жидкости отклоняются от закона Ньютона, то их называют неньютоновскими. К ним относятся жидкие полимеры, растворы высокомолекулярных полимеров, суспензии и др.
Макроперенос количества движения обусловлен конвективными токами, турбулентными образованьями, вихрями. Если микроперенос осуществляется только за счет теплового движения молекул, то макроперенос обусловлен не только молекулярным механизмом, но главным образом за счет более быстрого переноса макроколичеств среды. В результате этого в жидкости возникает дополнительное трение. Оно учитывается коэффициентом турбулентной вязкости т. Тогда формула (1.9) примет вид:
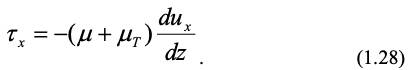
Можно показать [6], что в этом случае система уравнений Навье-Стокса формально останется той же (1.10), но вместо ньютоновской вязкости μ необходимо подставить в нее сумму ньютоновской и турбулентной вязкости μт.
Поле скоростей при микропереносе количества движения определяется при решении системы уравнений Навье-Стокса (1.10), а при макропереносе количества движения определяется из решения системы уравнений Навье-Стокса с учетом турбулентной вязкости. Следует отметить, что если ньютоновская вязкость является величиной постоянной для данной среды, то турбулентная вязкость зависит от масштаба турбулентности и поэтому при ее расчете, возникают определенные трудности.
1.8 Аналогия процессов переноса
Сравнивая выражения для трех видов молекулярного переноса массы (1.18) – закон Фика, переноса тепла (1.23) – закон Фурье и переноса количества движения (1.9) – закон Ньютона, нетрудно заметить, что по форме они абсолютно аналогичны.
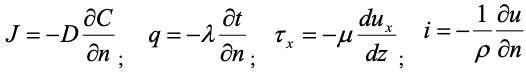
.
Здесь эти уравнения дополнены еще одним видом переноса – переносом электричества. Где u – градиент напряжения или электрический потенциал, ρ – удельное сопротивление электрического тока.
Имеется очевидное подобие выражений для конвективного переноса массы (1.22), переноса тепла (1.27) – закон Фурье и переноса количества движения (1.10), записанных ниже для одномерного потока:
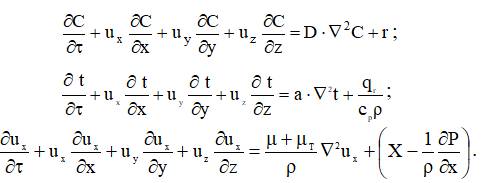
Приведенные уравнения тождественны по форме. Их левые части представляют собой, соответственно, скорость переноса массы, теплоты и количества движения в пространстве. Первые члены правой части представляют собой, соответственно, скорость молекулярного переноса массы, теплоты и количества движения, а вторые – характеризуют интенсивность внешнего источника. Одинаковая форма уравнений, описывающих разные виды переноса, указывает на подобие полей концентраций, температур и скоростей в рассматриваемых процессах.
На аналогию трех видов переноса указывает и одинаковая размерность коэффициентов переноса а, D и ν равная [м2/с]. Для газов механизм молекулярного переноса одинаков для переноса массы, теплоты и количества движения, т. к. связан с тепловым движением молекул. Поэтому все три коэффициента имеют один порядок с произведением длины свободного пробега молекул L на скорость их теплового движения u*:
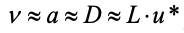
.
Для жидкостей соотношение этих коэффициентов следующее:
ν а D.
При турбулентном движении газа и жидкостей роль всех трех коэффициентов может играть коэффициент турбулентного обмена [10], равный для изотропной турбулентности произведению масштаба турбулентности l на среднюю пульсационную скорость u.
Подобие различных видов переноса позволяет использовать общий математический аппарат, общие методы решения уравнений, описывающих перенос. Для моделирования различных процессов переноса можно использовать метод электродинамической аналогии на аналоговых ЭВМ (подобие переносу электричества) или подобие другого вида переноса. Так, передаче тепла теплопроводностью соответствует молекулярный массоперенос, а передаче тепла конвекцией – конвективный массоперенос. Только передача тепла излучением (передача энергии в форме электромагнитных волн в инфракрасном спектре) не имеет аналогии в массопереносе.
Вследствие подобия теоретические и экспериментальные результаты исследования, например, процессов теплопереноса могут быть непосредственно применены к процессам диффузии и наоборот [10]. В то же время экспериментальное изучение теплопереноса проводится в среде с переменной температурой. При этом на результатах исследования сказывается зависимость физических констант от температуры и приходится использовать усредненные по температуре значения этих констант, что вносит погрешности в расчеты. По этой причине можно рекомендовать для получения более точных зависимостей для конвективного теплопереноса использовать метод аналогии с массопереносом. По этой же причине в данной монографии наибольшее внимание уделено массопереносу, а вопросы теплопереноса рассмотрены как вторичные.
1.9 Экспериментальный подход к исследованию процессов переноса
Как следует из вышеизложенного, расчеты процессов микро- и макропереноса достаточно сложны, т. к. необходимо решать систему уравнений в частных производных, причем расчеты конвективного переноса массы, теплоты и количества движения значительно сложнее молекулярного переноса. Решение такой системы уравнений возможно в ряде частных случаев, а в общем случае возможно только численными методами и поэтому прибегают к использованию эмпирических зависимостей.
Так для расчета процессов теплопереноса используют эмпирический коэффициент теплоотдачи , равный отношению потока тепла q к разности температур Δt. Тогда тепловой поток равен:

Распределение температур от одной среды к другой в стационарной теплопередаче (постоянство во времени потока тепла q) через стенку толщиной δ с коэффициентом теплопроводности приведено на Рис. 1.5.
Применяя уравнение (1.29) для 1-й и 2-й среды, с учетом теплопроводности через стенку толщиной δ и общего коэффициента теплопередачи К, получим равенство выражений для стационарного теплового потока:
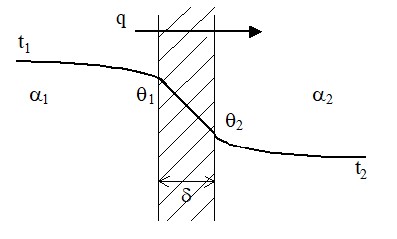
Рис. 1.5. Распределение температур при теплопередаче через стенку.
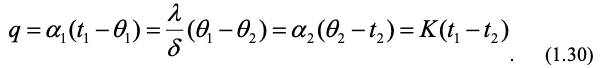
С учетом этих соотношений получим уравнение:

Физический смысл соотношения (1.31) заключается в том, что общее сопротивление теплопередачи через стенку 1/К равно сумме сопротивления переноса тепла от 1-й среды к стенке 1/α1, термосопротивления стенки δ/ и сопротивления переноса тепла от стенки ко 2-й среде 1/α2.
Аналогично для расчета процессов массопереноса используют эмпирические коэффициенты массопереноса К и массоотдачи .
Распределение концентраций вещества в стационарной массопередаче через поверхность раздела фаз от одной среды (газовая) к другой (жидкая) приведено на Рис. 1.6.
Коэффициенты массоотдачи для обеих сред могут быть найдены из выражения диффузионного потока, как выражения потока массы М на единицу поверхности:
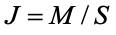
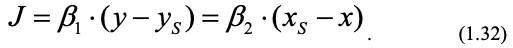
Значения концентраций на границе xs и уs трудноопределимы, поэтому записывают другое выражение диффузионного потока для коэффициентов массопереноса для первой среды К1 и для второй К2 через соответственно равновесные концентрации x* и y*.
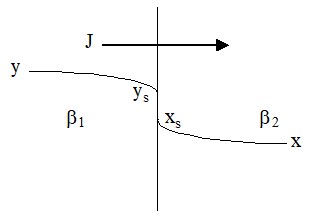
Рис. 1.6. Распределение концентраций при массопередаче через поверхность раздела фаз.
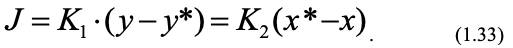
Обычно принимают линейный закон (m – константа равновесия, тангенс угла наклона линии равновесия) для определения равновесных концентраций на границе [6]:
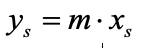
Из очевидного равенства:
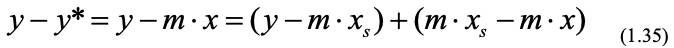
находим с учетом (1.32) и (1.33):
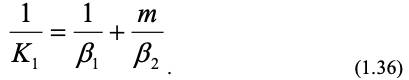
К1 – коэффициент массопереноса по газовой фазе.
Физический смысл соотношения (1.36) заключается в том, что общее сопротивление процесса массопередачи через межфазную поверхность 1/К1 равно сумме сопротивления переноса вещества от 1-й среды к межфазной поверхности 1/1 и сопротивления переноса вещества от межфазной поверхности ко 2-й среде m/2.
Аналогично можно получить закон сложения сопротивлений для коэффициента массопереноса по жидкой фазе:
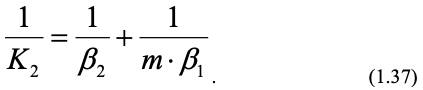
Сложность расчета по уравнениям (1.33) – (1.36), особенно в системах с подвижной поверхностью раздела фаз, заключается в том, что часто точно неизвестна ни поверхность раздела фаз, ни значения концентраций на ней, ни коэффициенты массопереноса.
Эмпирические коэффициенты тепло- и массоотдачи определяют на основании экспериментов, обработка которых проводится в виде критериальных зависимостей (зависимости между безразмерными параметрами), полученных на основании теории подобия.
1.10 Основы теории подобия
Экспериментальные исследования более удобно и экономически выгоднее проводить не на больших объектах, а на их моделях. Затем с помощью теории подобия можно распространить полученные на моделях опытные закономерности на подобные объекты другого масштаба.
Исходной предпосылкой теории подобия служит то, что подобные явления описываются одинаковыми уравнениями. Выше были рассмотрены общие уравнения переноса массы, тепла и количества движения. На практике приходится иметь дело с конкретными объектами моделирования и поэтому необходимо сформулировать условия, выделяющие рассматриваемое явление из общего класса явлений (условия однозначности). К ним относятся геометрическая форма и размеры системы (трубы, аппарата и т. д.), физические свойства ее (плотность, вязкость среды и др.), начальные условия (начальная скорость, температура и т. д.) и граничные условия, характеризующие свойства системы на ее границах.
Соотношения между сходственными величинами образца и модели называются константами (масштабами) подобия. Так для геометрического подобия – подобия геометрических размеров образца (l’ – длина, b’– ширина, h’– высота) и соответствующих размеров модели – l”, b”, h” получим константу геометрического подобия

Из этого выражения можно записать инварианты (симплексы) подобия, записав отношения параметров для образца и для модели, например:

Для подобия физических величин имеем константы подобия, например для кинематической вязкости и плотности:
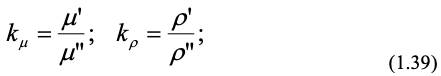
При моделировании процессов, связанных с изменением свойств системы во времени (нестационарных) должно соблюдаться временное подобие, тогда константа временного подобия:

Константы кинетического подобия включают отношение скоростей u и ускорений a в сходственных точках объекта и модели:
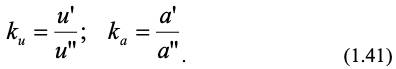
Следует отметить, что подобие кинетическое (подобие планов скоростей и ускорений) может иметь место только при наличии подобия геометрического.
Динамическое подобие описывается соотношениями сходственных сил, энергий и масс для модели и объекта, причем динамическое подобие может иметь место только при наличии подобия геометрического и кинетического.
1.11 Подобное преобразование дифференциальных уравнений переноса
Перенос количества движения. Рассмотрим динамическое подобие на примере подобного преобразования уравнения Навье-Стокса (1.10) для одномерного потока (перенос количества движения). В этом случае скорость потока
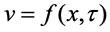
Запишем это уравнение для объекта:
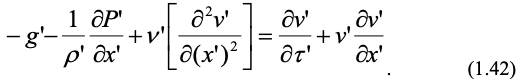
Аналогичное уравнение с учетом констант подобия запишем для модели:
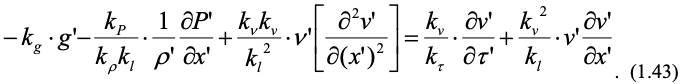
Чтобы уравнения (1.42) и (1.43) были идентичны, все множители из констант подобия должны быть равны, тогда:
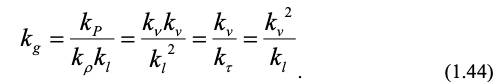
Домножив все члены уравнения (1.44) на kl /kv2, получим безразмерные соотношения:
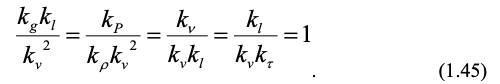
Эти соотношения после подстановки констант подобия дают выражения соответствующих критериев подобия Фруда, Эйлера, Рейнольдса и гомохнонности. Так для критерия Фруда .
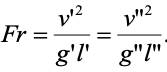
Опуская индексы, получим аналогично и другие критерии:
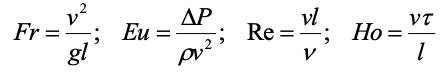
.
Для обеспечения подобия критерии подобия для объекта и модели должны быть численно одинаковы. Это положение определяет содержание 1-й теоремы подобия.
Так как члены уравнения Навье-Стокса представляют собой сумму удельных сил тяжести, давления, вязкости и инерции, то сравнивая их с выражениями критериев, можно сделать вывод, что критерий Фруда представляет собой отношение силы инерции к силе тяжести, критерий Эйлера – отношение силы давления к силе инерции, критерий Рейнольдса – отношение силы инерции к силе вязкости (учитывает режим движения) и критерий гомохронности – отношение инерционных сил модели и объекта (учитывает нестационарность процесса).
Обычно критерий Эйлера является определяющим и математическое описание явления переноса количества движения в критериальном виде с учетом геометрического критерия Г имеет вид:
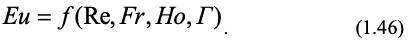
Таким образом, решение дифференциальных уравнений описывающих процесс можно представить в виде зависимостями между критериями подобия. Это положение известно как 2-я теорема подобия.
Выше было сказано, что для обеспечения подобия критерии подобия для объекта и модели должны быть численно равны, но тогда согласно зависимости (1.46) и определяющие критерии должны быть равны. Таким образом, для обеспечения подобия достаточно равенства определяющих критериев модели и объекта. Это положение определяет содержание 3-й теоремы подобия.
Положения, устанавливаемые тремя теоремами подобия, справедливы для любого вида переноса. Они используются как для постановки экспериментов, так и для математической их обработки.
Теплоперенос. Критерии теплопереноса выводятся аналогично выводу критериев переноса количества движения. Рассмотрим подобное преобразование уравнения Фурье-Кирхгофа (1.27) для одномерного теплопереноса, когда t = f (x, τ) в отсутствии источников тепла для объекта моделирования (индексы опустим):
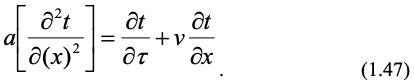
Аналогичное уравнение с учетом констант подобия запишем для модели:
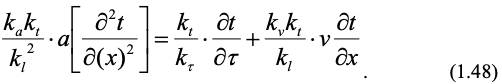
Чтобы уравнения (1.47) и (1.48) были идентичны, все множители из констант подобия должны быть равны, тогда:
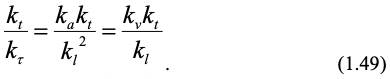
Из первого равенства выражения (1.49), подставив значения констант подобия, получим безразмерный комплекс – критерий Фурье, который характеризует изменение теплопереноса теплопроводностью во времени:

Из второго равенства выражения (1.49), подставив значения констант подобия, получим другой безразмерный комплекс – критерий Пекле, который представляет собой отношение теплопереноса за счет движения среды (конвективный) и за счет теплопроводности (молекулярный):