
Макрокинетика сушки
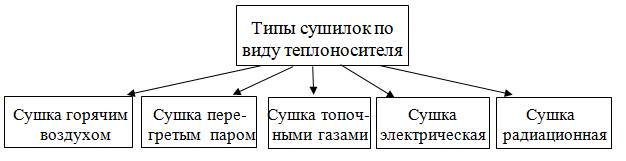
Рис. 2.1 Типы сушилок по виду теплоносителя (способу подвода тепла).
Представленные на Рис. 2.1 типы сушилок используют, как правило, конвективный отвод образующихся при сушке паров. Влагоносителем здесь является воздух. Влагоноситель – это агент, насыщающийся влагой, диффундирующей с поверхности высушиваемого материала. При сушке горячим воздухом он является тепло- и влагоносителем. В ряде методов сушки воздух является только влагоносителем.
Для интенсификации процесса сушки применяют и комбинированные сушилки, например, сушка горячим воздухом и радиационная, сушка горячим воздухом и микроволновая. Рассмотрим подробнее характеристики наиболее часто используемых тепло- и влагоносителей.
2.1 Водяной пар
Водяной пар предназначается для сушки различных, в том числе и термочувствительных материалов. Его используют как для нагрева высушиваемых материалов через проводящую тепло стенку в контактных сушилках, так и для подогрева в теплообменниках (калориферах) воздуха, который затем направляется в качестве теплоносителя в конвективные или другого типа сушилки. Иногда осуществляют сушку перегретым паром.
Пар – чистый теплоноситель, конденсат которого представляет собой дистиллированную воду. Температуру водяного пара легко регулировать путем его дросселирования. Он обладает высокой теплотой конденсации и высоким коэффициентом теплоотдачи; следовательно, расход его и требуемая поверхность теплообмена в теплообменнике при его применении невелики, в сравнении с другими теплоносителями. Кроме того, пар безопасен и в пожарном отношении.
Пар, температура которого равна температуре кипения воды tк при данном давлении, называется насыщенным. При отводе от него теплоты он превращается в воду – конденсируется, однако температура его tк при этом не изменяется. Поступающий из котельной пар всегда содержит некоторое количество воды в результате конденсации в паропроводе, и перед подачей на установку его обычно обезвоживают, используя конденсатоотводчик (конденсационный горшок).
Перегретым называется пар, температура которого tп.п выше температуры кипения воды tк при данном давлении. Получают его при перегреве насыщенного водяного пара в пароперегревателе. При охлаждении перегретый пар будет конденсироваться только тогда, когда его температура станет равной температуре кипения воды tк при данном давлении. Обычно пар перегревают настолько, чтобы он не конденсировался в паропроводе или чтобы он удалил всю влагу из материала при прямой сушке перегретым паром. При сушке перегретым паром он является также и влагоносителем.
В таблице 2.1 приведены для ряда значений абсолютного давления параметры насыщенного водяного пара: температура конденсации, плотность, теплота парообразования, его энтальпия и энтропия. Более подробная таблица приведена в Приложении. Аналогичные таблицы приведены также в литературе по тепломассообменным процессам [1, 4, 9].
Таблица 2.1 Параметры сухого насыщенного пара
Р – давление; t к —температура; ρ – плотность; r —теплота парообразования; h —энтальпия; S – энтропия.
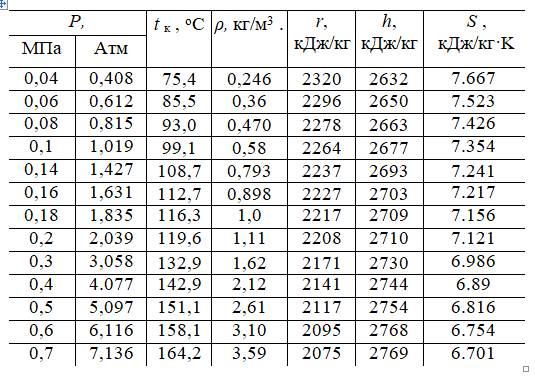
Теплота парообразования r – это количество тепла, необходимое для превращения 1 кг кипящей воды (при данном давлении) в сухой насыщенный пар. Энтальпия (теплосодержание) сухого насыщенного пара h равна энтальпии жидкости при температуре кипения tк плюс теплота парообразования r.

Аналогично энтропия сухого насыщенного пара S равна энтропии жидкости при температуре кипения tк плюс теплота парообразования r деленная на температуру кипения в градусах Кельвина.
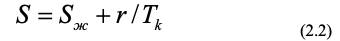
Значение коэффициента теплоотдачи α, характеризующего теплоперенос от насыщенного пара к нагреваемому им материалу, в среднем составляет 1500 Вт/(м2·К). Коэффициент теплоотдачи значительно уменьшается в случае присутствия в нем инертных примесей, обычно воздуха и воды, поэтому их количество должно быть минимальным.
Расход греющего пара в процессе сушки Gг определяют по уравнению:

где Q – количество теплоты, отдаваемое паром (рассчитывается по уравнению теплового баланса – см. ниже); r – теплота парообразования (табл. 1.1); х – степень сухости пара.
Степень сухости пара х – это массовая доля сухого насыщенного пара во влажном паре. Степень сухости насыщенного пара, часто в среднем принимают равной 0,95, это означает, что на 100 кг влажного пара приходится 95 кг сухого насыщенного пара и 5 кг воды.
Пример 1. Определить температуру и расход насыщенного водяного пара, поступающего в калорифер при избыточном (манометрическом) давлении 0,5 МПа, если его степень сухости 95%, а количество передаваемого паром в калорифере тепла 10000 Вт.
Решение: По табл. 2.1 для абсолютного давления 0,1+ 0,5= 0,6 (МПа) находим температуру пара 158,1 oС.
Расход греющего пара определяем по уравнению (2.3):
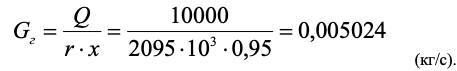
Здесь r = 2095 кДж/кг, также находится по таблице 2.1.
2.2 Горячий воздух
Воздух, обычно нагреваемый в калорифере водяным паром, является теплоносителем (сушильным агентом) и одновременно переносчиком паров воды, испарившейся за счет подведенного тепла из влажного материала. Таким образом, воздух в конвективных сушильных установках всегда влажный. Атмосферный воздух также содержит водяной пар, количество которого зависит от температуры воздуха, времени года, погоды и других местных условий.
Отдача теплоты нагретым воздухом стенке теплообменника приблизительно в 500 раз ниже, чем насыщенным водяным паром, поэтому нагретый воздух для сушки обычно используют при непосредственном контакте с влажным материалом.
Влажный воздух характеризуется следующими параметрами: температурой t, точкой росы tр, влагосодержанием d, абсолютной и относительной влажностью φ, энтальпией h и энтропией S.
Влагосодержание d – это количество содержащихся в воздухе водяных паров (в кг), отнесенное к 1 кг абсолютно сухого воздуха.
Абсолютная влажность – это масса водяного пара (кг), содержащаяся в 1 м3 влажного воздуха. Она равна плотности водяного пара ρп при температуре воздуха t и парциальном давлении пара рп.
Относительной влажностью φ называется массовое количество содержащихся в воздухе паров, отнесенное к содержанию их в состоянии насыщения при той же температуре, т. е. отношение плотности водяного пара к плотности насыщенного пара:

Относительная влажность берется в долях или процентах. Принимая, что влажный воздух подчиняется законам идеального газа, отношение плотностей (2.4) можно заменить отношением соответствующих давлений:

Относительную влажность воздуха определяют специальным прибором-психрометром, либо по диаграмме Рамзина h-d для воздуха (см. ниже). Влагосодержание воздуха определяется отношением плотности пара к плотности абсолютно сухого воздуха при той же температуре:

Ряд значений d для температур от 0 до 100°С и относительной влажности φ от 5 до 100% приведены в табл. 2.2 (для среднегодового барометрического давления 99,3 кПа, т. е. 745 мм рт. ст. [1]).
Для установления аналитической связи между влагосодержанием и относительной влажностью φ запишем выражение (2.6) с учетом уравнения Менделеева-Клайперона:
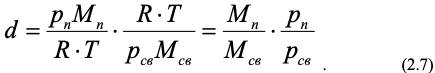
Таблица 2.2 Влагосодержание воздуха d · 103 кг/кг при различных φ и t для давления 745 мм рт. ст. (99,3 кПа)
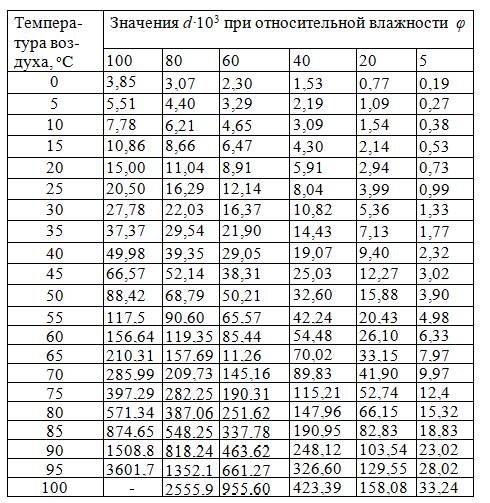
Подставляя мольную массу воды Мп = 18 и мольную массу абсолютно сухого воздуха Мсв = 29, с учетом (2.5) и закона Дальтона, согласно которому давление рсв равно разности общего давления влажного воздуха Р и парциального давления водяного пара в нем рп получим выражение:
Точка росы достигается при температуре tр, которую будет иметь воздух с влагосодержанием d в результате его охлаждения до состояния насыщения (φ = 1, в процентах – 100%, т. е. при температуре насыщения в данной точке tн).
Энтальпия h влажного воздуха – это количество содержащейся в нем теплоты, отнесенное к 1 кг сухого воздуха при той же температуре. Отсчет ведут от 0°С. Величина h равна сумме энтальпий 1 кг сухого воздуха и энтальпии для d кг водяного пара:
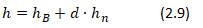
где hв = сcвt – энтальпия сухого воздуха, t – его температура и сcв – теплоемкость (обычно принимают среднюю, не зависящую от температуры 1,01 кДж/кг·К); hn —энтальпия водяного пара.
Энтальпия водяного пара определяется как сумма
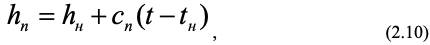
где: hн – энтальпия насыщенного водяного пара, сп – теплоемкость перегретого водяного пара и tн – температура насыщения. Применяя предложенную Рамзиным линейную зависимость от температуры, имеем [1].
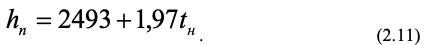
Эта зависимость применима и для перегретого пара и равна сумме теплосодержаний при 0 оС (2493 кДж/кг) и тепла перегрева от 0 до t оС. Аналогично определяется энтропия влажного воздуха:
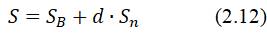
Величину энтропии воздуха удобнее определять по Т-S диаграмме для воздуха [1].
Для определения параметров воздуха удобно пользоваться также диаграммой Рамзина [1] в координатах энтальпия h – влагосодержание d. Угол между координатными осями на такой диаграмме равен 135°, но для расчета пользуются вспомогательной осью d, проведенной под углом 90° к ординате. Диаграмма h-d для воздуха представлена на Рис. 2.2. В более крупном масштабе в единицах системы СИ эта диаграмма дана также в приложении. На ней нанесены изотермы – линии постоянных температур (они идут с наклоном относительно горизонтали) и пучок расходящихся кривых, построенных по уравнению (2.8), выходящих из точки t = – 273 °С и d = 0, каждая из которых соответствует постоянному значению относительной влажности φ.
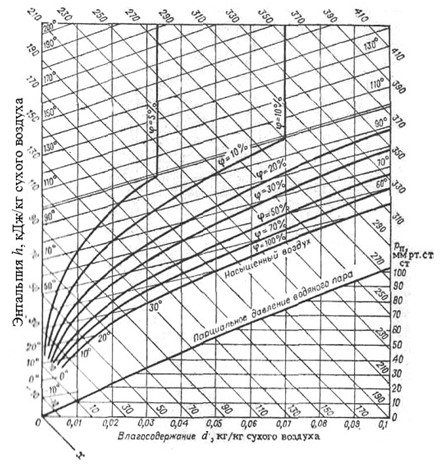
Рис. 2.2. Диаграмма h-d для воздуха.
При температуре 99,4 °С давление насыщенного пара становится равным среднему барометрическому, т. е. 745 мм рт. ст., для которого и составлена диаграмма. Если температура воздуха выше температуры насыщения, то максимальное давление водяного пара будет равно барометрическому В и относительная влажность воздуха, согласно (2.5) определится как:

Тогда с учетом отношения (2.13) уравнение (2.8) примет вид:
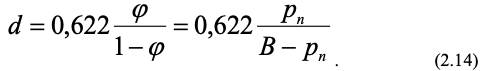
Из уравнения (2.14) следует, что при температурах выше 99,4 °С кривые для φ не зависят от температуры. Поэтому эти кривые на диаграмме при t = 99,4 °С (температура кипения воды) имеют перелом и далее идут почти вертикально. Отклонение их от вертикали связано с тем, что плотность перегретого пара в некоторой степени зависит от температуры.
Линия насыщенного пара φ = 100 % является граничной между областью влажного воздуха (выше неё) и двухфазной областью насыщенного пара с капельками воды (ниже неё), где использование полученных выше формул для смеси сухого воздуха и водяного пара неправомерно. Пересечение изотерм (линий постоянных температур) с линией насыщенного пара φ = 100 % дает точку конденсации (точка росы) tр.
По уравнению парциального давления водяного пара [1]:

из центра координат на h-d диаграмме проведена наклонная прямая. Определяют парциальное давление пара по заданному его влагосодержанию d, проводя соответствующую вертикаль до пересечения с прямой линией, построенной по уравнению (2.15) и затем из точки пересечения проводят горизонталь вправо до шкалы рп (1 мм рт.ст. = 133,3 Па).
Каждая точка диаграммы определяется двумя параметрами по пересечению 2-х линий. Остальные параметры точки находят по диаграмме. Рассмотрим примеры определения параметров влажного воздуха с помощью h-d диаграммы.
Пример 2. Определить энтальпию, влагосодержание, точку росы влажного воздуха и парциальное давление водяного пара при t = 60 °С и φ = 40%.
Решение. По диаграмме h-d (Рис. 2.2) находим точку пересечения изотермы t = 60 °С с линией φ = 40%. Этой точке соответствуют: энтальпия h = 205 кДж/кг сухого воздуха, влагосодержание d = 0,055 кг/кг сухого воздуха, точка росы tр= 43 °С. Схема решения примера дана на Рис. 2.3, а. Влагосодержание для заданных условий по Таблице 2.2 составит d = 0,05448 кг/кг, а расчет энтальпии по уравнению (2.9) дает (кДж/кг):
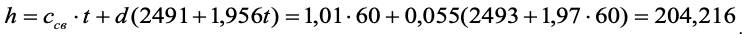
По диаграмме h-d (Рис. 2.2) находим также точку пересечения влагосодержания d = 0,055 кг/кг с линией парциального давления водяного пара и по шкале справа находим парциальное давление пара рп = 60 мм рт.ст. Расчет парциального давления водяного пара по уравнению (2.15) для общего давления Р = 745 мм рт. ст. дает близкое значение
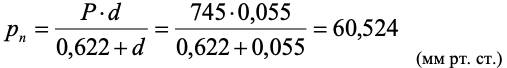
Пример 3. Определить относительную влажность воздуха, точку росы и парциальное давление водяного пара при t = 90°С и влагосодержании d = 0,07 кг/кг сухого воздуха.
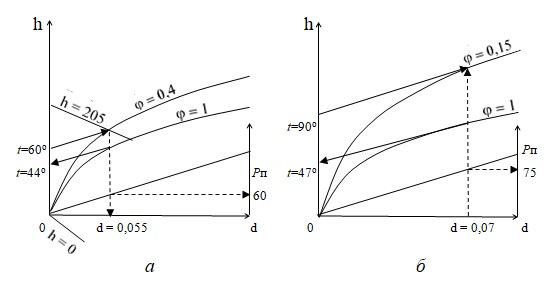
Рис. 2.3. Схема решений примеров по диаграмме h-d для воздуха: а—к примеру 2, б—к примеру 3.
Решение. По диаграмме h-d (Рис. 2.2) находим точку пересечения изотермы t = 90 оС с линией постоянного влагосодержания d = 0,07 кг/кг сухого воздуха. Этой точке соответствует относительная влажность воздуха φ = 15% и точка росы tр= 47 оС. Схема решения дана на Рис. 2.3, б. Затем по диаграмме h-d (Рис. 2.2) находим точку пересечения влагосодержания d = 0,07 кг/кг с линией парциального давления водяного пара и по шкале справа находим парциальное давление пара рп = 75 мм рт.ст. Расчет парциального давления водяного пара по уравнению (2.15) при общем давлении Р = 745 мм рт. ст. дает близкий результат:
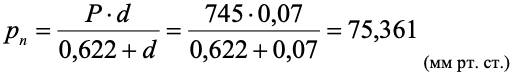
2.3 Изменение состояний воздуха при сушке на h-d диаграмме
При конвективной сушке сушильный агент – воздух предварительно нагревается в калорифере от температуры t0 до температуры t1, необходимой для сушки (Рис. 2.4, а). Соответствующие значения энтальпии составят h0 и h1. При этом влагосодержание воздуха d остается постоянным, а относительная влажность φ – уменьшается. На диаграмме h-d этот процесс изображается вертикальным отрезком АВ (от точки А к точке В). Расход тепла в калорифере:
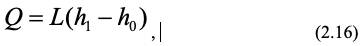
где L – расход сухого воздуха.
Процесс охлаждения воздуха на диаграмме также изображается вертикально, но в противоположном направлении. Если охлаждение воздуха идет до температуры насыщения tн, линия идет вниз до пересечения с линией φ =100% (отрезок ВС). Точка пересечения линий d = const и φ == 100% (точка С на Рис. 2.4, а) характеризует состояние воздуха в результате его охлаждения при d = const (точка росы). Изотерма, проходящая через эту точку, определяет температуру точки росы tр. Дальнейшее охлаждение воздуха ниже температуры точки росы (например, до температуры tп) приводит к конденсации из него части влаги и соответственно – к уменьшению его влагосодержания от d0 до dп. На диаграмме процесс охлаждения насыщенного воздуха совпадает с линией φ = 100% (кривая СЕ).
После нагрева воздуха в калорифере (линия АВ, Рис. 2.4, а) он поступает в сушилку. Если влага из материала будет испаряться только за счет тепла, передаваемого материалу воздухом, и отсутствуют теплопотери или дополнительный нагрев в сушилке (политропная сушка), то энтальпия воздуха после сушки h2 будет равна его энтальпии перед сушкой h1, так как все тепло, отданное воздухом на испарение влаги, возвращается обратно в воздух с удаляющимися из материала парами (адиабатическая сушка). Одновременно в сушилке понижается температура, увеличиваются влагосодержание и относительная влажность воздуха. Такой процесс носит название теоретического процесса сушки (h2 = h1 = h = const, линия ВD на Рис. 2.4, а).
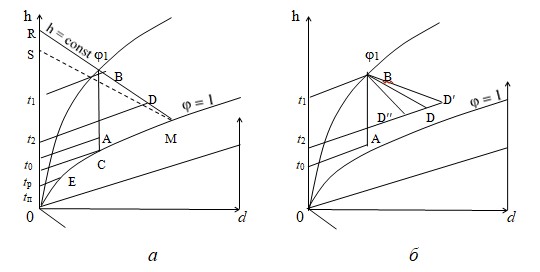
Рис. 2.4 Изменение состояний воздуха на h-d диаграмме:
а – при нагреве (АВ) охлажденнии (ВАСЕ) и сушке (ВD)
б – линии сушки: адиабатическая (ВD), с теплопотерями (ВD′′) и с подводом тепла в сушилке (ВD′).
Для сушильной практики большое значение имеет понятие о теоретическом процессе адиабатического испарения в системе поверхность испарения – воздух. В этом процессе воздух только испаряет, но не нагревает влагу. Непосредственно над поверхностью испарения воды (а в равной степени и над поверхностью влажного материала в начальный период сушки) образуется слой насыщенного пара (φ = 100%), находящегося в равновесии с водой. Температура влаги при этом имеет постоянное значение, равное температуре мокрого термометра tм. Данная температура в процессе испарения не меняется, в то время как температура воздуха по мере его насыщения все время понижается, приближаясь в пределе к температуре мокрого термометра tм (при φ = 100%). Эту температуру, которую примет воздух в конце процесса насыщения, называют также температурой адиабатического насыщения. Поступающая в воздух испаренная влага W вносит в него некоторое количество тепла W∙c∙tм, поэтому адиабатический процесс охлаждения воздуха в этом случае происходит с повышением его энтальпии (h2>h1). С учетом расхода сухого воздуха L на испарение получим:
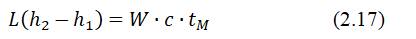
или

где с – теплоемкость воды.
Величина W/L – отражает увеличение влагосодержания воздуха в процессе его адиабатического охлаждения, оно равно (dм-d1), где dм—влагосодержание воздуха при его полном насыщении влагой при температуре мокрого термометра tм. Тогда при d1= 0 (уравнение оси ординат) получим

Уравнение (2.19) служит для нанесения на h-d диаграмму линий адиабатического насыщения воздуха.
Если, например, из точки М (см. Рис. 2.4, а) провести линию h1 = h2 = соnst до пересечения с осью ординат и отложить от точки пересечения R в масштабе, выбранном для энтальпий, отрезок RS, равный dм∙с∙tм , то полученная точка S и будет искомой, а прямая SМ будет линией адиабатического насыщения воздуха. Эту линию иногда называют также линией постоянной температуры мокрого термометра (tм = соnst) потому, что мокрый термометр, помещенный в воздух, насыщение которого происходит по линии адиабатического насыщения, будет показывать постоянную температуру tм. На h-d диаграммах для воздуха часто наносят пунктиром линии tм = соnst (см. на Рис. 2.4, а и приложение).
Приборы, состоящие из сухого и мокрого термометров (психрометры), широко используются в сушильной практике. Значение tм определяют с помощью термометра, нижний конец которого обернут влажной тканью («мокрый» термометр). Для получения надежных данных приток тепла излучением к нему должен быть минимален (экранирование при скорости воздуха около 5 м/с). По разности показаний «сухого» термометра (температура которого равна температуре воздуха tв) и мокрого термометра tм, пользуясь h-d диаграммой находят относительную влажность воздуха φ и другие его параметры (влагосодержание, энтальпия и парциальное давление водяного пара). Для этого по изотерме для температуры tм находят ее пересечение с линией φ = 100% (Рис.2.4, а). Далее двигаясь по линии постоянной температуры мокрого термометра (tм = соnst) доходят до пересечения с изотермой для температуры сухого термометра tв. В точке пересечения находят искомое значение φ и другие параметры.
Для более точного определения характеристик воздуха необходимо ввести поправку А на скорость движения воздуха u, м/с (обычно u>0,5 м/с) в месте установки психрометра [1] по уравнению:
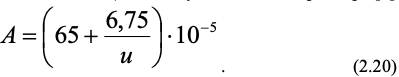
С учетом этой поправки парциальное давление водяного пара в движущемся воздухе находится как
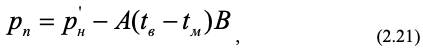
где рн’– давление насыщенного водяного пара при температуре мокрого термометра; В – барометрическое давление, атм.
На Рис. 2.4, б показаны варианты процесса сушки от температуры t1 на входе до температуры t2 на выходе из сушилки. Линия ВD соответствует процессу в теоретической сушилке (h = соnst). Линии действительной сушки проходят либо выше нее ВD’, с повышением энтальпии (при подводе дополнительного тепла в сушилку), либо ниже ВD” с понижением энтальпии (при наличии теплопотерь в окружающую среду, на нагрев материала, на нагрев транспортных устройств). По линии теоретической сушки (адиабатического насыщения воздуха влагой) на h-d диаграмме для воздуха происходит изменение его параметров (температуры, влагосодержания и относительной влажности) за счет адиабатического испарения свободной поверхностной влаги в начальный первый период сушки.
Разность между температурой воздуха (сухого термометра) tс и температурой мокрого термометра tм, характеризует способность воздуха поглощать влагу из материала и носит название потенциала (движущей силы) сушки ε:
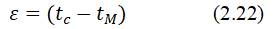
Потенциал сушки характеризует скорость испарения влаги из материала, которая зависит от состояния воздуха и температуры процесса, т. е. определяется совместным влияниям тепло- и массообмена. Когда воздух полностью насыщается влагой (tв = tм), потенциал ε становится равным нулю, и сушка прекращается.
Более удобно определять потенциал сушки по ε-d диаграмме (Рис. 2.5), предложенной Г. К. Филоненко [2], дающей связь между ε, d и tм. Она построена в более простых, прямоугольных координатах.
Поскольку теплота испарения, теплоемкость влажного воздуха и диффузионный критерий Прандтля, в сущности, не зависят от давления, то линии адиабаты (h = соnst) и температуры мокрого термометра (tм = соnst) на h-d диаграмме для воздуха одни и те же для разных давлений. Это дает возможность ее использовать при давлениях, отличных от атмосферного, с корректировкой других параметров диаграммы.
Следует отметить, что рассмотренная в данном разделе h-d диаграмма для воздуха дает возможность определить лишь статические его параметры и не описывает кинетику происходящих процессов.