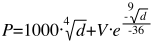Критерий Лейбница
Потом он взглянул на студента.
– Маррон! – позвал он его по фамилии после секунды размышления. Маррон сразу же вышел вперед, гордый, что ректор вспомнил его фамилию. – Иди за мной! – добродушно распорядился МакКинток.
Они вышли и направились к столовой. Через несколько минут приехал служитель на велосипеде и передал ректору ключи, а потом быстро уехал туда, откуда прибыл.
– Вот, – вложил МакКинток ключи в руки Маррона. – Открой, возьми то, что надо, хорошо закрой и сразу же верни ключи моей секретарше. Все ясно?
– Конечно. Спасибо, ректор МакКинток.
Ректор попрощался с ним и отправился в свой кабинет, напевая себе под нос.
Маррон вошел внутрь и сразу же нашел упаковку с томатной пастой. Она была повреждена лишь слегка, к счастью. Он взял ее и увидел, что внутри соуса была призма. Тогда Маррон вытер все, используя бумажные салфетки, которые имел с собой, потом закрыл дверь и отправился в приемную МакКинтока, чтобы вернуть ключи.
Как жаль, что этот соус испортился. Он был очень вкусным...
Войдя в лабораторию, Маррон увидел, что атмосфера там царила довольно мрачная.
– Проблема здесь, – говорил Шульц, показывая на раковину. – Триада смешения определяется параметрами K9, K14 и R11, но функция, которая этим управляет, показывает ясно, что энергия, необходимая для обмена, увеличивается в кубической пропорции к расстоянию.
– Я вижу, – констатировал Дрю, глядя на функцию. – Вы посчитали какие-то практические случаи?
– Мы с Камарандой не спали до двух ночи, чтобы понять поведение системы, но нам это пока не удалось. Пока, чтобы произвести обмен на расстоянии 100 километров, нужны 64 киловатта, что немного. Но чтобы произвести обмен на 200 километров, необходимы уже 512 киловатт. Это энергия, которую использует средняя мануфактурная фабрика.
– А для 1000 километров нужны будут 64 мегаватт17, – добавил Камаранда. – Необходима маленькая электростанция.
– Вот почему система обмена проходит просто на маленьких дистанциях. Для 300 метров отсюда до кабинета профессора Брайс использовалось всего 2 милливатта, – быстро посчитал Дрю, записывая на доске. – Меньше, чем нужно для мерцания LED.
– Это отлично подходит для небольших расстояний, диагностических или терапевтических, – вмешалась Брайс.
– Ну да, – ответил Дрю. – Но длинные дистанции вне досягаемости. Как исследование Вселенной.
Он вздохнул, опустив руки вдоль тела. МакКинток, однако, был бы доволен, потому что одно лишь лечение людей принесло бы кучу денег, но Дрю-то был физиком, и его коллеги изначально приоткрыли двери целого мира. Теперь он подошел к перспективе воображаемых исследований, спустившись с небес на землю. Он не мог с этим смириться. Ему надо найти другое решение.
– Мы только в начале, – заявил он. – Если мы будем настойчивы, может, мы найдем несколько факторов, которые позволят нам исключить это ограничение.
– Этим мы и занимаемся, – сухо сказала Новак.
Брайс заметила, что норвежка в тот день носила блузку с длинным рукавом, закрывающим запястья.
«Странно, – подумала она. – Вчера она была с короткими рукавами. Для нее, привычной к холодному климату, английский март должен казаться жарким. Кто знает, почему она переоделась».
Женщина не могла не заметить эти детали.
Маоко между тем внимательно разглядывала доску, скрестив руки. Кобаяши в сотый раз изучал раздаточный материал и каждый раз проверял несколько расчетов, производя записи на листок.
– А что если пока мы углубленно изучим теорию, экспериментируя с биологическими формами? – предложил Маррон.
Дрю посмотрел на профессора Брайс.
– Начнем с растений. Я позабочусь об образцах, – кивнула она и вышла.
– А я пока пойду и раздобуду инструмент более точный, чем микрометр. Нам надо отрегулировать вторую машину, – сказал Дрю, направляясь в лабораторию метрологии.
Маррон начал подготавливать первую машину, пока два японца занялись второй. Они общались на родном языке по поводу некоторых технических деталей, пока ожидали нового измерительного прибора.
Через полчаса Брайс положила на пластину А первой машины лист зеленого салата.
Они активировали машину, и лист переместился туда, где была банка с водой. Биолог взяла его и посмотрела в портативный микроскоп, который носила с собой. Через несколько минут она подняла глаза от окуляров.
– Кажется, все отлично. Прожилки, стомы, клетки... Насколько я вижу, все на месте.
Дрю удовлетворенно кивнул.
Они попробовали с цветами, корнеплодами, грибами и даже с маленьким бонсаем, растущим в горшке. Все предметы оставались целыми после перемещения.
Тем временем Маоко подрегулировала промежуток между сетками на второй машине, используя более точный инструмент.
Они положили зерно фасоли на пластину второй машины и провели эксперимент. Фасоль оказалась примерно в трех метрах слева от банки с водой – точное расстояние между двумя машинами.
Брайс быстро проверила зернышко и нашла его в отличном состоянии.
– Перейдем к мясу, – сказала она.
Она уже принесла его, извлекая из сумки бифштекс, упакованный в термическую пленку.
Маррон жадно посмотрел на нее. Он уже был голоден к одиннадцати утра. Профессор Брайс с угрюмой улыбкой взглянула на студента и передала ему пустую сумку, чтобы он положил ее куда-нибудь. Парень подмигнул ей, шутливо изображая разочарование.
Брайс взяла нож в кухонном уголке лаборатории и отрезала кусочек бифштекса квадратной формы стороной примерно в 4 сантиметра. Толщина составляла примерно восемь миллиметров.
Они переместили кусок с помощью второй машины и исследовали его в микроскоп, удостоверяясь, что все в порядке.
Маррон попробовал его.
– Вкус тот же самый. Консистенция тоже. Я бы сказал, что перемещение никак его не испортило.
– Так и должно быть, поскольку теория говорит о том, что машина обменивает непосредственно два объема в пространстве независимо от их содержания, – прокомментировал Дрю. – Что скажете, если попробуем с животной формой?
Профессор Брайс несколько мгновений раздумывала над этим, потом решила:
– Да, попробуем. Мы должны будем провести анализ по молекулярной биологии на уже перемещенных образцах, чтобы быть совершенно уверенными, но до сих пор полученные результаты подтверждают теорию обмена в пространстве. – Она поразмышляла еще несколько минут. – Исходя их биоэтических соображений, попробуем с формами, лишенными нервной системы. Если что-то пойдет не так, они, по крайней мере, не будут страдать. Увидимся после обеда, – сказала она и вышла.
Дрю и остальные сконцентрировались на теории в поисках решения проблемы мощности.
– Что-то ускользает от нас, – сказал Шульц. – Как мы поняли к настоящему моменту, активация машины создает сверхпространственный коннектор между объемами пространства, тянущийся от пластины А до пластины B. Коннектор подчиняется времени Планка18, и в этот момент два пространства меняются местами.
– Если он действительно сверхпространственный, тогда мы деформируем очень плотное пространство, – вмешался Кобаяши. – Только так оправдывается необходимость такой большой мощности, повышаемой с расстоянием.
– Кажется, так, – согласился Шульц.
– Попробуем кое-что представить, может, нам это поможет, – вмешался Камаранда. Он приянл кафедральный тон, будто давал лекцию своим студентам. – Все мы живем в пространстве, которое считаем трехмерным, имеющим длину, ширину и высоту. Мы знаем, что тяжесть деформирует пространство, и это уже приводит нас в затруднение, потому что мы не можем понять эту ситуацию. Используем классическое подобие эластичной ленты, которая представляет трехмерное пространство. Если мы положим на эту ленту предмет, то он ее деформирует, прогибая под своим весом. Чем более тяжелым будет предмет, тем больше будет деформация, то есть прогиб ленты. Под весом мы подразумеваем массу, которая не зависит от тяжести, но ее порождает. Таким образом, мы видим, что увеличение массы приводит к увеличению деформации. Если мы положим на ленту второй объект меньшей массы, он скатится, приблизившись к предмету с большей массой. Такое поведение мы определим, как гравитационное притяжение. На самом деле предмет с меньшей массой тоже деформирует пространство в свою очередь, следовательно, происходит гравитационное притяжение в сторону более тяжелого предмета, но в меньшей степени. По аналогии с эластичной лентой, которая двухмерна, мы можем понять концепцию деформации пространства под силой тяжести. Она деформирует ленту перпендикулярно поверхности ленты, добавляя фактически размер к его геометрии. Предположим теперь, что мы возьмем нашу эластичную ленту и положим ее на гелевую пластину, которая, как мы знаем, является твердым эластичным коллоидом, легко деформируемым. Машина, с которой мы экспериментируем, расположена в трехмерном пространстве, которое представлено эластичной лентой, и, по-видимому, когда она активируется, то непосредственно приближается к гелевой пластине, являющейся дополнительным аспектом. Заметьте, что деформация порции геля создает канал, или Коннектор, который своими концами воздействует на эластичную ленту, то есть пространство, и обменивает между ними порции пространства, с которыми она соединена. После обмена Коннектор рассеивается, а гель возвращается к своему нормальному состоянию. – Камаранда сделал паузу после долго объяснения, а потом продолжил дальше свои рассуждения: – Очевидно, гель очень плотный, следовательно, требуется много энергии, чтобы сделать его жидким. По каким-то причинам, которых мы не знаем, Коннектор определяется только временем Планка, хотя воздействие энергии значительно большее, чем воздействие времени. За него мы принимаем полсекунды, верно? – спросил он, оборачиваясь к Кобаяши, который кивнул ему в ответ. – Должно быть что-то, что препятствует существованию Коннектора во времени, превышающим время Планка. Если бы он держался дольше, что бы случилось? Возможно, два пространства успели бы обменяться еще раз? Или это повлекло бы за собой постоянный обмен пространствами? Я не думаю, чтобы это являлось проблемой для геометрии пространства. Просто, дезактивируя машину, два пространства остались бы в последней достигнутой конфигурации. Может быть также, что если бы Коннектор длился дольше времени Планка, случился бы парадокс, свойства которого на данный момент я не могу представить, и только некий неизвестный закон природы вмешивался бы, чтобы помешать этому.
Все молчали, раздумывая над рассуждениями индийского математика.
Через несколько минут Новак вскочила на ноги, побледнев.
– О, Боже! – воскликнула она взволнованно.
Все испуганно посмотрели на нее.
– Нет никакого парадокса, – мрачно продолжила она. – Есть ошибка, однако!
Она подошла к доске и стерла часть с таким трудом найденных уравнений, будто они были написаны каракулями какого-то злостного студента. Она нарисовала эластичную ленту сверху, соединив два ее конца.
– Это Коннектор, как мы его назвали, – показала она на провод. – Он только что включен и начался обмен. Мы в нулевом времени процесса. Объем пространства А стартует и входит в коннектор. Как и в какой форме – мы не знаем. Но он начинает двигаться к противоположному концу. Одновременно объем пространства B делает тоже самое со своей стороны и начинает двигаться к противоположной стороне Коннектора. Проходит время Планка, и два пространства прибывают в место назначения, выходят из Коннектора и оказываются на месте друг друга. Мы во времени 1, и процесс закончен. – Она сделала эффектную паузу. – Но между временем 0 и временем 1, – сказала она голосом с нарастающей интенсивностью, – что находится на месте этих пространств, которые перемещаются по Коннектору? – закончила она истерическим криком.
На мгновение все были неподвижны.
– Нет…, – произнес Камаранда со стеклянным взглядом.
– Напротив, да! – закричала она еще громче. – Нет Ничего! – жестко добавила она.
У Дрю волосы встали дыбом.
Кобаяши открыл рот и снова закрыл.
Лицо Шульца больше походило на маску, сделанную в момент отсутствия всякого выражения.
Маррон смотрел перед собой отсутствующим взглядом.
Маоко, напротив, с довольным видом и странной улыбкой смотрела на Новак.
– Ничего – вы это понимаете? – продолжила норвежка. – И вероятно, именно там оказывается вся та энергия, которая вытекает из расчетов. Энергия, которая выходит из нашего мира, нарушая его энергетическое равновесие. Это нарушение постулата Ловозера, согласно которому ничего не создается и ничего не разрушается, но все трансформируется. И, возможно, именно поэтому Коннектор может по максимуму поддерживаться на время Планка, иначе Ничего поглотило бы всю энергию, которая вокруг него. Если бы у него было больше времени, возможно, оно бы забрало бы всю мировую энергию!
В лаборатории наступила могильная тишина.
Это было похоже на лед темноты, более глубокой, чем может себе представить человек. Лед, который кристаллизировал их ум и сознание.
Новак стояла рядом с доской с мелом в руках.
С минуту никто не двигал ни одним мускулом. Потом Кобаяши подошел к доске, взял мел и сделал несколько расчетов на свободной поверхности доски.
– Нет, – сказал он, наконец. – Так не может быть. Функция триады показывает, что мощность увеличивается только в кубической пропорции независимо от объема обмененного пространства. Предположим, мы сделаем этот объем постоянным, тогда он определит, сколько энергии, которую мы используем для эксперимента, поглотит «Ничего», пока два пространства направляются к своим точкам назначения. Я не вижу, почему, увеличивая дистанцию обмена при постоянном объеме, Ничего должно увеличивать свою поглощающую способность.
Новак смотрела на него широко раскрытыми глазами, усиленно размышляя. Через несколько бесконечных секунд она поморщилась, бледнея еще больше.
– Нет… нет… Это безумие, непостижимо, – пробормотала она. – Не может быть.
– Что такое, профессор Новак? – обеспокоенно спросил Кобаяши.
– Это! – показала Новак на нарисованный на доске Коннектор. Все непонимающе посмотрели на доску. – Но вы не понимаете? – закричала она. – Мы деформируем именно Ничего! Коннектор формируется в Ничем! Сделан из Ничего! Пространство А входит в Ничего и появляется в точке B, которые оказывается в пункте А, проходя через Ничего!
Это повергло присутствующих в тотальную прострацию. Земля словно уплыла у них из-под ног. Будто все предельно понятные вещи, все основы, на которых базировались их знания, неожиданно разлетелись на куски.
– Но как может… как может нечто, что существует… – отважился произнести Дрю, – нечто, что существует… войти в Ничего, прекращая существовать, и появиться из Ничего, начав снова существовать, как и раньше, но в другом месте?
Новак положила себе руку на лоб и прислонилась к доске. Казалось, что у нее закружилась голова. Маоко подошла к ней и, взяв под локоть, подвела к близстоящему стулу. Потом она поднесла ей стакан воды, который норвежка приняла с благодарным взглядом.
– Это вопрос исключительно философский, – ответила Новак Дрю тихим спокойным голосом, пока пила. – Или лучше скажем, что был бы вопросом исключительно философским, если бы мы не стояли перед лицом экспериментального проявления манипуляции Ничем. Ничто не существует и не может быть даже определено, иначе его определение сделало бы Ничто существующим. Но мы им манипулируем. Я чувствую, что это так. Я не вижу других решений. При увеличении расстояния обмена увеличивается длина Коннектора, состоящего из Ничего и сделанного из Ничего. Поскольку очевидно, что Ничего поглощает с максимальной эффективностью энергию, которая ему подается, отсюда следует вывод, что Коннектор поглощает всю энергию. При увеличении длины Коннектора, увеличивается также чрезмерность энергии, необходимой для управления и сохранения Коннектора в течение времени Планка. Коннектор производит обмен, да, но по недостижимой цене на мизерных дистанциях.
Снова молчание, но в этот раз на лицах Дрю, Шульца, Камаранды, Маррона и Кобаяши ясно читалось восхищение гениальной интуицией Новак. Они увидели, что ум этой женщины обнаружил то, что они не могли видеть, и привел их туда, куда они не могли прийти. В то же время их лица выражали отчаяние от поражения, потому что эти догадки приводили к непреодолимым препятствиям.
– Это крах… Чистое крушение, – пробормотал Шульц, качая отрицательно головой.
Прошло пару минут, потом спокойно и беспечно Маоко села на угол рабочей поверхности радом с сидящей Новак. Она посмотрела на нее сверху вниз и сказала дружеским тоном, удивив присутствующих, которые даже не заметили стакан воды, который она ей предложила:
– Профессор Новак, Ваше заявление говорит о том, что не существует никаких практических решений проблемы, поскольку наш мир является изолированной системой, а машина существенно потребляет энергию извне этой системы, нарушая ее энергетическое равновесие.
Новак кивнула.
– Но если вместо того, чтобы считать наш мир изолированной системой, посчитать его просто закрытой системой19, помещенной внутрь большей системы, Вы не думаете, что мы могли бы без затруднений изучить ее поведение?
Новак изумленно уставилась на Маоко широко раскрытыми глазами.
Никто не смел говорить, учитывая масштабность такой гипотезы.
Через несколько мгновений Шульц поднялся с нахмуренным лбом и подошел к доске, взяв с собой ручку и лист бумаги. Он перенес на бумагу все написанные уравнения, потом полностью вытер доску. Затем он начал усиленно писать мелом, начав с фундаментальных уравнений термодинамики, заменяя его составные части теми результатами, которые они получили в своей теории.
Дрю с Марроном тут же оказались рядом с ним, чтобы помочь, а Камаранда, встав за его спиной, внимательно следил за математической частью его работы. Кобаяши сосредоточенно смотрел на доску, на которой появлялась новая потрясающая форма концепции мира.
И никто не заметил, как сидящая на рабочем столе в нескольких метрах сзади них Маоко нежно поглаживала своей маленькой ручкой светлые волосы Новак, лаская ее.
Глава XIV
К двум часам дня профессор Брайс вошла в лабораторию, принеся с собой коробку, из которой то и дело раздавались неожиданные звуки.
Все сразу же осознали, что никто так и не выходил из лаборатории, не ходил обедать. Кто-то писал на доске уравнения и корректировал графики, кто-то на свободных столах неистово писал на листах бумаги и что-то считал, пользуясь калькулятором. Время от времени кто-то листал раздаточный материал, сверял данные и вносил их в свои уравнения, а потом шел дальше в своих исследованиях.
Брайс поставила коробку на полку и села в уголок в ожидании. Она понимала, что нужно подождать подходящего момента. Об этом говорили изнуренные лица коллег, неистово работающих с крайней сосредоточенностью.
Камаранда стоял у стола, склонившись над листом бумаги. Он закончил последние расчеты и записал результаты на лист. Потом быстро произвел еще какие-то расчеты, кивнул, поднялся и направился к Шульцу, прихватив свой лист.
– Энтропия равна 415J/K20.
Шульц записал значение в функцию на доске.
– Кобаяши, у тебя есть результат по энергии?
Японец заканчивал вычисления очень сложного интеграла. Он поднял руку, призывая подождать несколько минут, пока он проводил расчеты на калькуляторе. Потом он записал результаты на листок, еще раз проверил и, поняв, что все правильно, изрек:
– 163000 Дж21.
Шульц внес также и эти значения. Потом свои результаты работы сообщили Дрю и Маррон.
– Речь идет о толщине покрытия, равного двум миллиардам световых лет. Это лучшее приблизительное значение, которое мы можем тебе дать на настоящий момент.
Немец записал результат уравнения на график некой сферы, покрытой концентрической оболочкой.
Новак, стоявшая у доски с Шульцем, начала расписывать уравнение с только что полученными данными.
Из-за стола поднялась сияющая Маоко и подошла к доске с раздаточным материалом в одной руке и со своими пометками в другой. Указав пальцем на таблицу в инструкции, она сказала:
– Есть! Параметр R6! – триумфальным тоном воскликнула она. – Он составляет 190 микровольт.
Шульц написал 190*10-6 вместо x в формуле и произвел расчеты. Потом он застыл в ожидании Новак, которая вскоре представила ему некоторые результаты своих расчетов. Шульц внес их вместе со своими данными в новое уравнение.
Несколько минут он судорожно проводил вычисления под наблюдением своих коллег и, наконец, получил конечный результат. Уравнение теперь было сокращено до нескольких факторов и робко ждало последних шагов, чтобы узнать результат.
Он протер покрасневшие глаза, очерченные черными кругами, глубоко вздохнул и продолжил расчеты. Оставалось найти последнее число, которое он написал справа, будто не видя его.
Он не мог этому поверить.
Но это было именно так.
Новак кивнула, а за ней Камаранда и Дрю. Маоко и Кобаяши победно улыбались, глядя то на доску, то на коллег. Маррон обессиленно облокотился на стол.
– Термодинамическая система уравновешена, – заявил Шульц формально. – Принимая Вселенную за закрытую термодинамическую систему, помещенную внутрь оболочки толщиной в два миллиарда световых лет, и устанавливая параметр R6, рассчитанный мисс Ямазаки, мы можем определить триаду перемещения за счет обмена объемами пространства, среди которых известна любая точка Вселенной, с интервалом, определенным длиной Планка. Теперь обмененный объем входит в уравнение, используемое в предыдущей ситуации, но необходимая максимальная мощность для обмена объема, равного одному кубическому метру на расстоянии 10 миллиардов световых лет, составляет 5 гигаватт. Это, конечно, огромная мощность, но необходима специальная электростанция, но она доступна и достигаема.
Профессор Брайс подошла к ним.
– Могу я узнать, что произошло?
– Мы переделали концепцию вселенной, – сказал Дрю эмоционально. – Своеобразное функционирование машины обмена заставило нас развить модель, на которой до сих пор основывалась наука. Отныне термодинамическая система должна рассматриваться, как состоящая из толстой оболочки, внутри которой находится наша Вселенная. Оболочка и наша Вселенная могут обмениваться энергией в двух направлениях, при этом сохраняя постоянным энергетический баланс. Закон сохранения энергии сохраняется в такой модели, где оболочка является простой метафорой, позволяющей управлять термодинамикой внутри системы и заставляющей ее функционировать. С пространственно-временной точки зрения оболочка не является физической единицей, поскольку в реальности она приближается на пространственном уровне к пространственно-временной материи известной Вселенной. Это позволяет машине функционировать, потому что каждая точка нашей Вселенной является близлежащей к точке оболочки. Когда машина активируется, пластина А приближается к близлежащей точке на оболочке, как если бы открылась некая дверь, и порождает канал перемещения, который мы назвали Коннектор. Другой его конец находится в другой точке нашей Вселенной, установленной заданными нами параметрами. Поворотный параметр, R6, приводит к тому, что обмен объемами между пространствами A и B может осуществляться с использованием доступного количества энергии.
Биолог поняла только в общих чертах речь Дрю, но ей этого хватило. Важно, что все функционировало.
– Мы должны дать название этой новой модели, – заметил Маррон.
– Правильно! – согласился Камаранда, гуру математических моделей. – Я предлагаю назвать ее просто Система. Это просто для запоминания и быстро для произношения.
– Я согласен, – сказал Дрю. – Что скажете? – обратился он к другим.
– Для меня нормально, – ответил Шульц, и другие тоже поддержали его.
– Отлично, – произнес Дрю. – Теперь все-таки всем надо перекусить! – распорядился он.
Маррон был последним, кто покинул лабораторию. На пороге двери он обернулся и посмотрел на доску, где красовалось конечное уравнение по расчету мощности. Оно было невероятно простым по сравнению с неимоверными усилиями, затраченными на его поиск, и выглядело так22: