Чудеса арифметики от Пьера Симона де Ферма

3.3.1. Ошибки великих и письмо-завещание Ферма

Самая ранняя из известных версий теоремы дана в «Началах Евклида», книга IX, предложение 14:

Если число будет наименьшим измеряемым <данными> первыми числами, то оно не измерится никаким иным первым числом, кроме первоначально измерявших <его>.

Далее разъясняется: «Пусть число A будет наименьшим измеряемым первыми числами B, C, D; я утверждаю, что A не измерится никаким иным первым числом, кроме B, C, D». Доказательство этой теоремы только на первый взгляд выглядит убедительно, и эта видимость основательности усиливается цепочкой ссылок: IX-14 → VII-30 → VII-20 → VII-4 → VII-2. Однако здесь допущена элементарная и даже очень грубая ошибка. Её суть в следующем:

Пусть A=BCD, где числа B, C, D простые, (первые). Если допустить теперь существование простого E, отличного от B, C, D, и такого, что A=EI, то делается вывод, что в этом случае A=BCD не делится на E. Это последнее утверждение неверно, поскольку теорема ведь ещё не доказана и не исключено, например, BCD=EFGH, где E, F, G, H простые числа, отличные от B, C, D. Тогда A:E=BCD:E=EFGH:E=FGH, т.е. в этом случае станет возможно, что число A может делиться на число E и тогда доказательство теоремы опирается на аргумент, который ещё не доказан, поэтому конечный вывод неверный. Та же ошибка может попасть и в другие теоремы, использующие разложение целых чисел на простые множители. Видимо, из-за архаичной лексики «Начал Евклида», даже такой великий учёный как Эйлер не обратил должного внимания на эту теорему, иначе вряд ли бы он стал использовать на практике «комплексные числа», которые ей не подчиняются.

Такая же история произошла и с Гауссом, который, также не заметил этой теоремы в «Началах» Евклида, но всё же сформулировал её, когда в ней возникла необходимость. Формулировка и доказательство Гаусса следующие:

«Каждое составное число может быть разложено на простые сомножители только одним единственным образом.

Если мы предположим, что составное число A, равное aαbβcγ…, где a,b,c,… обозначают различные простые числа, разложимо на простые сомножители ещё и другим способом, то прежде всего ясно, что в этой второй системе сомножителей не может встречаться других простых чисел, кроме a,b,c,…, т.к. составленное из этих последних число A не может делиться ни на какое другое простое число» [11, 25].

Это почти точное повторение ошибочной аргументации в доказательстве Евклида. Но если эта теорема не доказана, то всё построенное на натуральных числах основание науки рушится, а все следствия из определений и аксиом теряют свою значимость. И как же теперь быть? Ведь если с доказательством теоремы не справились такие гиганты науки как Евклид и Гаусс, то куда уж нам-то грешным. Но выход всё-таки есть, и он указан в одном удивительном документе, называемом «Письмо-завещание Ферма».

Это письмо было отправлено Ферма в августе 1659 г. его давнему другу и бывшему коллеге по парламенту Тулузы королевскому библиотекарю Пьеру де Каркави, от которого его получил известный французский учёный Христиан Гюйгенс (Christiaan Huygens), первым возглавивший созданную в 1666 г. Французскую Академию Наук. Здесь мы приведём только отдельные выдержки из этого existписьма Ферма, которые нас особенно интересуют [9, 36].

«Сводка открытий в науке о числах. …

1. Поскольку обычные методы, изложенные в Книгах, не достаточны для доказательства очень трудных предложений, я нашёл, наконец, для их решения совершенно особый путь. Я назвал этот способ доказательства бесконечным или неопределённым спуском. Сначала я пользовался им только для доказательства отрицательных предложений, как, например: …что не существует прямоугольного треугольника в числах, площадь которого была бы квадратом». Подробности см. Приложение II.

Наукой о числах названа арифметика и дальнейшее содержание письма не оставляет в этом никаких сомнений. Именно с арифметики начинаются не только математические, но и все другие науки. А в самой арифметике метод спуска один из основополагающих. Далее даются примеры задач, решение которых без этого метода не только очень затруднено, но иногда и вообще вряд ли возможно. Здесь мы назовём только некоторые из этих примеров.

«2. Долгое время я не мог приложить мой метод к утвердительным предложениям, потому что обходы и окольные пути для достижения цели гораздо более трудны, чем те, которые послужили мне для отрицательных предложений. Поэтому, когда мне надо было доказать, что каждое простое число, которое превосходит на 1 кратное четырех, состоит из <суммы> двух квадратов, я был в сильнейшем затруднении. Но, наконец, многократно повторенные размышления пролили свет, которого мне не доставало, и утвердительное предложение стало возможным трактовать моим методом с помощью некоторых новых принципов, которые необходимо было к ним присоединить. Этот прогресс в моих рассуждениях для случая утвердительных предложений таков: если некоторое простое число, которое превосходит на единицу кратное 4-х, не состоит из двух квадратов, то имеется простое число той же природы, меньшее данного, а затем третье, ещё меньшее, и т.д. спускаясь до тех пор, пока не придёте к числу 5, которое является наименьшим из всех чисел этой природы. Оно, следовательно, не может состоять из двух квадратов, что, однако имеет место. Отсюда можно заключить путём доказательства от противного, что все простые числа этой природы должны состоять из двух квадратов».

Эту теорему Ферма своим способом впервые доказал Эйлер в 1760 г. [38], а в рамках очень сложной «Арифметики вычетов» Гаусса эта теорема доказывается в одном абзаце [23]. Однако повторить доказательство самого Ферма никому так и не удалось. «… 3. Имеется бесконечно много вопросов такого рода, но существуют и другие, которые требуют новых принципов для применения к ним метода спуска… Таков следующий вопрос, который Баше, как он сознаётся в своём комментарии к Диофанту, не смог доказать. По этому поводу Декарт в своих письмах сделал такое же заявление, признаваясь, что считает его настолько трудным, что не видит никакого пути для его решения. Каждое число есть квадрат или состоит из двух, трех или четырех квадратов».

Ещё раньше 22 года назад в октябре 1636 года письмом к Мерсенну Ферма сообщал о той же задаче как о своём открытии, но в общем виде, т.е. для любых многоугольных чисел (напр., треугольников, квадратов, пятиугольников и т.д.). Впоследствии он даже назвал эту теорему золотой. Следовательно, метод спуска был открыт им в самом начале его исследований по арифметике. К моменту написания письма-завещания Ферма уже знал от Каркави, что вопрос о создании Французской Академии наук практически решён и ему нужно лишь дождаться окончания строительства здания, чтобы сбылась мечта всей его жизни стать профессиональным учёным, причём в ранге академика. Гюйгенсу было поручено собрать материалы первых академических изданий. Для них Ферма предлагал открытый им метод спуска и решение на его основе конкретных арифметических задач.

Однако о том, что эти задачи очень трудны, мало кто знал и Ферма было понятно, что опубликуй он их решения, то они вообще не произведут никакого впечатления. У него уже был такой опыт и теперь он приготовил настоящий сюрприз. Для тех, кто не оценит по достоинству его решения, он предложит решить ещё одну задачу. Это основная теорема арифметики, имеющая особую значимость для всей науки, поскольку без неё вся теория теряет силу. Ферма обнаружил в доказательстве Евклида ошибку и пришёл к выводу, что доказать эту теорему без применения метода спуска чрезвычайно трудно, если вообще возможно. Однако теперь-то мы можем раскрыть и эту тайну с помощью наших возможностей заглянуть в тайник Ферма с «еретическими письменами» и вернуть его утраченное доказательство науке в виде представленной ниже реконструкции.

3.3.2. Доказательство Ферма

Итак, чтобы доказать основную теорему арифметики, предположим, что существуют равные натуральные числа A, B, состоящие из разных простых множителей:

A=B где A=pp1p2 …pn; B=хx1x2 …xm ; n≥1; m≥1 (1)

В силу равенства чисел A, B каждое из них делится на любое из простых чисел pi или xi. Каждое из чисел A, B может состоять из любого набора простых множителей, в т. ч. и одинаковых, но при этом среди них нет ни одного pi равного xi, иначе в (1) они были бы сокращены. Теперь (1) можно представить, как: pQ=xY где p, x – минимальные простые числа среди pi, xi; Q=A/p; Y=B/x (2)

Поскольку множители p, x разные, условимся, что p>x; x=p–δ1, тогда pQ=(p–δ1)(Q+δ2) где δ1=p–x; δ2=Y–Q (3)

Откуда следует: Qδ1=(p – δ1)δ2 или Qδ1=xδ2 (4)

Уравнение (4) – это прямое следствие предположения (1). Правая часть этого уравнения содержит в явном виде простой множитель x. Однако в левой части уравнения (4) число δ1 не может содержать множитель x, т.к. δ1=p–x не делится на x из-за того, что p – простое число. Число Q также не содержит множитель x, т.к. по нашему предположению оно состоит из множителей pi, среди которых нет ни одного равного x. Таким образом, справа в уравнения (4) есть множитель x, а слева его нет. Тем не менее нет оснований утверждать, что это невозможно, т.к. мы изначально допускаем существование равных чисел с разными простыми множителями. Тогда остаётся лишь признать, что если существуют натуральные числа A=B, составленные из разных простых множителей, то необходимо, чтобы в этом случае существовали и другие натуральные числа A1= Qδ1 и B1=xδ2; также равные между собой и составленные из разных простых множителей. Если учитывать, что δ1=(p–x)

Теперь мы получаем ситуацию, аналогичную ситуации с числами A, B, только с меньшими числами A1, B1. Анализируя затем (5) изложенным выше способом, мы будем вынуждены признать, что должны существовать числа A2=B2, где A2

Следуя этим путем, мы неизбежно придем к случаю, когда существование чисел

Ak=Bk, где Ak

С другой стороны, даже заблуждаясь в этом вопросе, т.е. считая, что эта теорема была доказана ещё Евклидом, как наука могла её игнорировать, используя «комплексные числа» и обрекая себя тем самым на разрушение изнутри? И наконец, как же можно объяснить, что эта очень простая, по сути, теорема, на которой держится вся наука, вообще не преподаётся в средней школе?

Что же касается метода спуска, то данное доказательство является одним из самых простых примеров его применения, что встречается довольно редко из-за широкой универсальности этого метода. Гораздо чаще для применения метода спуска требуется большое напряжение мысли, чтобы подвести под него логическую цепь рассуждений. С этой точки зрения могут быть поучительны и некоторые другие особые примеры решения задач этим методом.

3.4.1. Немножко «остроты ума» для очень трудной задачи

Мы рассмотрим теперь ещё один пример задачи из письма-завещания Ферма, которая сформулирована там следующим образом:

Существует только один целый квадрат, который, увеличенный на два, даёт куб, этот квадрат равен 25.

Когда по предложению Ферма её попытался решить лучший английский математик того времени Джон Валлис (John Wallis), то он был очень сильно раздосадован и вынужден признать, что не может это сделать. Более двух веков считалось, что решение этой задачи получил Леонард Эйлер, но его доказательство основано на применении «комплексных чисел», а мы-то знаем, что это вовсе не числа, т.к. они не подчиняются основной теореме арифметики. И только в конце ХХ века Андрé Вейль (André Weil) с помощью метода треугольников Ферма, всё-таки сумел получить доказательство [17]. Это был большой прогресс, т.к. здесь использован чисто арифметический метод, однако применительно к данной задаче он явно был притянут за уши. Мог ли Ферма решить эту задачу проще? Ответ на этот вопрос мы также извлечём из тайника, что позволит нам раскрыть и эту тайну науки в виде следующей реконструкции. Итак, мы имеем уравнение p3=q2+2 с очевидным решением p=3, q=5. Для доказательства утверждения Ферма, предположим, что существует ещё одно решение

P>p=3, Q>q=5, которое удовлетворяет уравнению

P3=Q2+2 (1)

Поскольку очевидно, что Q>P, то пусть

Q=P+δ (2)

Подставляя (2) в (1), получим:

P2(P–1)–2δP–δ2=2 (3)

Здесь нам потребуется самая малость «остроты ума», чтобы заметить, что δ>P, иначе уравнение (3) невыполнимо. Действительно, если сделать пробу δ=P, то слева (3) будет:

P2(P–4)>2, что не подходит, следовательно, должно существовать число δ1=δ–P. Тогда, подставляя δ=P+δ1 в (3), получим

P2(P–4)–4δ1P–δ12 = 2 (4)

Теперь-то мы непременно заметим, что δ1>P, иначе по той же логике, что и выше, слева (4) мы получим:

P2(P–9)>2, что опять-таки не подходит, тогда, должно существовать число δ2=δ1–P, и подставляя δ1=P+δ2 в (4), получим:

P2(P–9)–6δ2P–δ22=2 (5)

Вот здесь-то уже можно совсем не сомневаться, что так будет продолжаться без конца и края. Действительно, путем проб δi=P каждый раз мы получаем P2(P−Ki)>2. Каким бы ни было число Ki, это уравнение невыполнимо, поскольку если Ki

3, то P2(P−Ki)>2, а если Ki≥P, то такой вариант исключается, т.к. тогда P2(P−Ki)≤0. Продолжать так бесконечно явно бессмысленно, следовательно, наше начальное предположение о существовании других решений P>3, Q>5 неверно и эта теорема Ферма доказана.

В часто упоминаемой нами книге Сингха эта задача приводится как пример «головоломок», которые «придумывал» Ферма. Но теперь выясняется, что универсальный метод спуска и простой приём с пробами приравненных чисел делают эту задачу одним из очень эффективных примеров для обучения в школе. Имея это доказательство, школьники без труда смогут доказать ещё одну теорему из письма-завещания Ферма, которую в своё время мог решить только такой знаменитый на весь мир учёный, как Леонард Эйлер:

Существуют только два целочисленных квадрата, которые, увеличенные на 4, дают кубы, эти квадраты будут 4 и 121.

Иными словами, уравнение p3=q2+4 имеет только два решения в целых числах.

3.4.2 Золотая теорема Ферма

Напомним, что в известном нам письме-завещании Ферма, (п. 3.3.1), изложен только частный случай этой теоремы для квадратов. Но и этот упрощённый вариант задачи оказался не по силам не только представителям высшей французской аристократии Баше и Декарту, но даже и королевско-императорскому математику Эйлеру.

Другой королевский математик Лагранж, благодаря тождеству, найденному Эйлером, всё же сумел справиться с квадратами и его доказательство только одного этого частного случая ЗТФ тиражируется до сих пор чуть ли не во всех учебниках. Однако, не поддаётся никакому разумному объяснению то, что общее доказательство ЗТФ для всех многоугольных чисел, полученное Коши в 1815 г., было просто проигнорировано научным сообществом.

Наше исследование мы начнём с формулировки ЗТФ из письма Ферма к Мерсенну 1636 г. следующим образом:

Всякое <натуральное> число равно

одному, двум или трём треугольникам,

одному, 2, 3 или 4 квадратам,

одному, 2, 3, 4 или 5 пятиугольникам, и так до бесконечности [31].

Поскольку многоугольные числа явно не в почёте у сегодняшней науки, мы дадим здесь все необходимые разъяснения. Формула вычисления любого многоугольного числа представляется как mi =i+(k−2)(i−1)i/2 где m – многоугольное число, i – порядковый номер, k – количество углов.

Таким образом, m1=1; m2=k; а для всех остальных i значения mi варьируются в широких пределах, как показано в Табл. 1.

Для вычисления mi достаточно получить по формуле только треугольные числа, что очень легко, поскольку разница между ними с каждым шагом растёт на единицу. А все остальные mi можно вычислять путём прибавления в столбцах предыдущего треугольного числа. Например, в столбце i=2 числа увеличиваются на единицу, в столбце i=3 – на три, в столбце i=4 – на шесть и т.д., т.е. как раз на величину треугольного числа из предыдущего столбца.

Табл. 1. Многоугольные числа

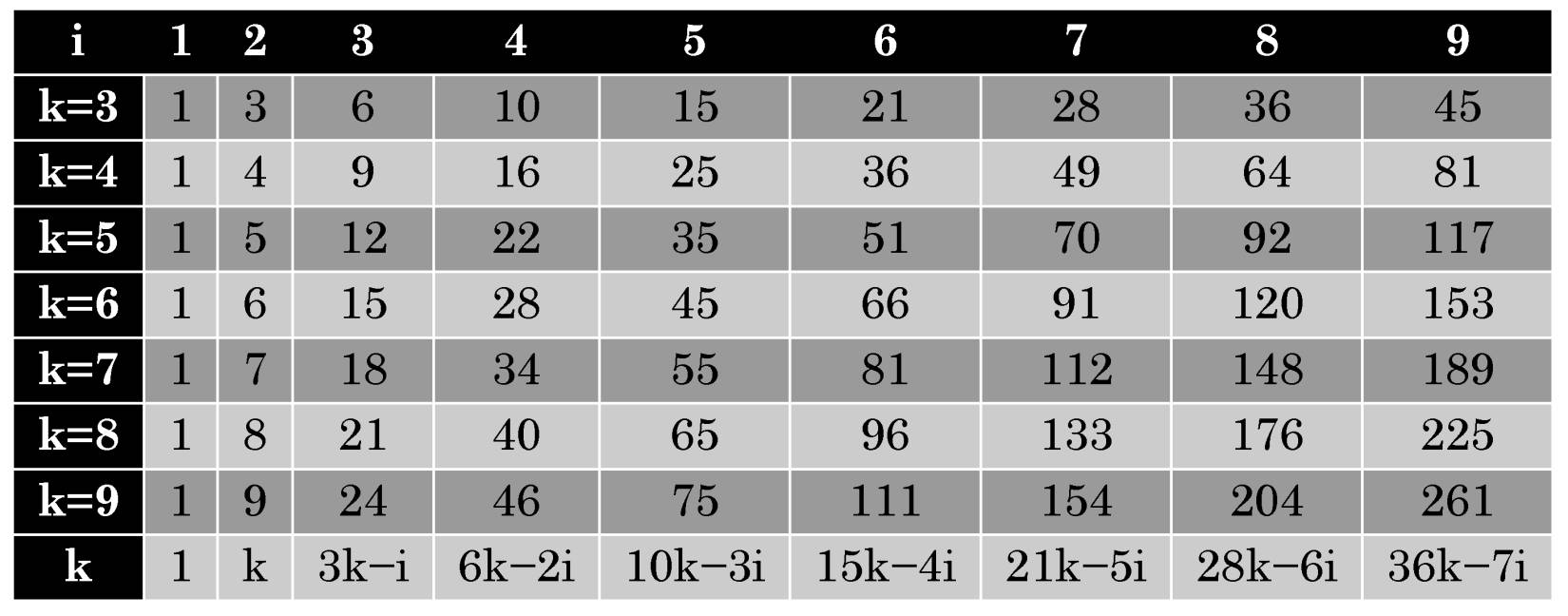
Убедиться в том, что любое натуральное число представляется суммой не более чем k k-угольных чисел, довольно легко. Например, треугольное число 10, состоит из одного слагаемого. Далее 11=10+1, 12=6+6, 13=10+1 из двух, 14=10+3+1 из трёх, 15 вновь из одного слагаемого. И так будет происходить регулярно со всеми натуральными числами. Удивительно то, что количество необходимых слагаемых ограничивается именно числом k. Так что же это за чудодейственная сила, которая неизменно даёт такой результат?

Для примера возьмём натуральное число 41. Если в качестве слагаемого будет ближайшее к нему треугольное число 36, то уложиться в три многоугольных числа не получится никак, поскольку иначе как из 4-х слагаемых, т.е. 41=36+3+1+1 это число не получается. Однако, если мы вместо 36 возьмём другие треугольные числа, например, 41=28+10+3, или 41=21+10+10, то опять каким-то неведомым чудесным образом всё будет так, как утверждает ЗТФ.

На первый взгляд представляется просто невероятным, что можно как-то с этим разобраться? Но мы всё же обратим внимание на существование особых натуральных чисел, которые представляются не менее, чем из k k-угольных чисел и обозначим их как S-числа. Такие числа легко найти, например, для треугольников – это 5, 8, 14, для квадратов – 7, 15, 23, для пятиугольников – 9, 16, 31 и т.д. И вот такое простое наше наблюдение позволяет двигаться к цели напрямую, т.е. не задействуя хитроумные приёмы или мощную «остроту ума».

Теперь, чтобы доказать ЗТФ, предположим обратное, т.е. что существует некое минимальное натуральное число N, представляемое не менее, чем из k+1 k-угольных чисел. Тогда понятно, что это наше предполагаемое число должно находиться между какими-нибудь k-угольными числами mi и mi+1 и может представляться как