 0
0Los problemas de matemática en la práctica didáctica
• VII tipo: aprendizaje de reglas. Entre tanto se debe aclarar qué se entiende por “regla”. Se puede pasar de reglas sencillas a reglas muy complejas. Las primeras se pueden simplificar mediante frases en las que se den condiciones a respetar (por ejemplo: «En alemán el artículo determinativo “die” acompaña un sustantivo femenino»). En este caso, se trata de una asociación verbal que comunica una idea que se debe tener presente como regla. O sea: no basta con saber repetir la concatenación verbal para poder decir que se ha aprendido la regla; a lo sumo se sabrá expresar la regla. Ocurre saberla aplicar en un cierto número de ejemplos significativos. Por lo tanto, una regla es una cadena de dos o más conceptos. Ésta puede ser expresada por medio de formulaciones como «Si A entonces B» («Si hay un sustantivo femenino, entonces debo precederlo de “die”»). A propósito del estilo más eficaz para aprender reglas, hay quien afirma que consiste en dar la regla en modo explícito y luego pedir que se use en varios ejemplos; otros en cambio sugieren el procedimiento inductivo inverso: dar ejemplos a partir de los cuales se pueda obtener la regla (proceso de descubrimiento). Los segundos temen que se puedan utilizar formulaciones verbales como atajos y que en lugar de cadenas conceptuales se llegue a obtener solo cadenas verbales. (El ejemplo clásico es aquel del estudiante que sabe “decir” la regla con palabras, pero que no sabe aplicarla en un caso concreto).
• VIII tipo: problem solving. Adquiridas las reglas, ya hemos visto en que sentido el ser humano pude resolver problemas. Por lo tanto, aceptando esta escala, se trata del aprendizaje más elevado y significativo. La acción de resolver un problema se concluye, en estos casos, en un aprendizaje realmente sustancial. La mutación de las capacidades del individuo es tan claro y explícito como en cada uno de los otros tipos de aprendizaje. El aprendizaje mediante problem solving lleva a nuevas capacidades del pensamiento.
Los ocho tipos de aprendizaje van, en la escala proporcionada por Gagné (1973), del más simple al más complejo y completo; y cada uno es prerrequisito para el o los sucesivo/s (aunque se puede hacer directamente una distinción, V tipo, a través de estímulo/respuesta, I y II tipo). Los estudios al respecto son tan vastos y profundos que no me puedo ni limitarme a recordarlos (remito a los textos citados sucesivamente, que son ricos en bibliografía pertinente). Termino entonces confesando a los lectores que expuse, en esta sección, una teoría casi ingenua, básica, no la más moderna; lo que es suficiente para nuestro objetivo (actualmente, por ejemplo, no se acepta esta tipología lineal, sino que se prefiere una más ramificada). En las indicaciones bibliográficas aconsejaré lecturas mucho más actualizadas sobre estos fascinantes temas y volveré sobre este argumento más adelante.
En el caso particular de la Matemática, los tipos que más nos interesan siguiendo las mismas fuentes son:
• Tipos I y II: señales y S/R. Este tipo de aprendizaje parece ser la base de la adquisición de ideas y conceptos matemáticos sucesivos de gran importancia. Es sobre estos tipos de aprendizaje que nos debemos basar para entender el interesante fenómeno por el cual, aún en edad preescolar e incluso antes del kínder, el niño aprende Matemática, tanto así que hoy en día los programas de Matemática de la escuela primaria en todo el mundo sugieren no subestimar las competencias matemáticas precedentes de los niños, sino valorizarlas y basar en ellas las nuevas ideas que se busca formar. Un análisis de las “capacidades matemáticas básicas” (para caracterizarlas, en el pasado, sugerí un sustantivo bastante afortunado: “protomatemática”) es una actividad intelectual muy estimulante. Se pueden añadir los nombres de los números, los nombres de algunas figuras recurrentes en geometría, la actividad de imitar dibujos con el lápiz, la denominación de la sucesión de los números naturales, etc. Cabe precisar que ninguno de estos aprendizajes es “adulto”, completo o preciso. Por ejemplo, no es seguro que los nombres de los números correspondan exactamente a los números mostrados (un caso común es el del niño que muestra tres dedos y dice «Dos»); no es seguro que el nombre de una figura sea el que un adulto diría (un caso común : el bloque con forma de triángulo es llamado “techo” por la función que cumple en la construcción de las casitas); la sucesión de los números puede ser correcta en términos de ritmo pero avanzar saltuariamente en cuanto al nombre de los números (uno, dos, tres, seis, nueve, […]). Sin embargo, en la base de cada uno de estos aprendizajes, hay una respuesta de tipo matemático importante provocada por señales y estímulos. Por ejemplo, en la base de la sucesión de los números, aun siendo incompleta, hay una consciencia confusa que se está consolidando:
• cada número tiene su propio nombre;
• cada número tiene un sucesivo bien determinado;
• se empieza con uno;
Empezando con un número bien definido como primero, cada uno de los demás se obtiene adicionando una unidad.
• Tipo III: concatenación. Al contrario de lo que se piensa, el aprendizaje por concatenación no verbal está presente como fundamento de adquisiciones importantes en Matemática, relacionadas, por ejemplo, con la escritura al hacerse dueño de letras, símbolos y figuras geométricas.
• Tipo IV: asociación o secuencias verbales. En este caso, viene inmediatamente a la mente la secuencia de los números naturales de la que hablé anteriormente. Sin embargo, mientras precedentemente no hablé más que de un hecho fonético, aquí la interiorización es tal que se puede hablar del aprendizaje de la secuencia (nótese: aunque ésta sea incompleta). Esto juega un rol importante en el aprendizaje matemático del niño; por ejemplo, el momento en el que el niño ve 6 objetos y usa el número cardinal 6. Esto puede darse:
• a simple vista; en tal caso, parecen tener un rol una o más configuraciones particulares (estudiadas por la psicología de la forma, la Gestalt; retomaré este tema ampliamente más adelante);
• por conteo: 1, 2, 3, 4, 5, 6, donde el último número ordinal es el número cardinal del conteo. En este caso, los niños tienen diferentes estilos. Hay quien dice el sustantivo 6 con un tono diferente, casi de descubrimiento. Hay quien cuenta hasta 6 y luego repite el número 6. El tipo IV no se limita solamente a los primeros años de vida del niño, por el contrario, permanece en el tiempo y lo acompaña durante su vida de (…) aprendiz de Matemática. Aprender los signos de las operaciones, las letras que representan elementos geométricos, los nombres de figuras jamás vistas, etc., todo lo que está relacionado con este mismo tipo de aprendizaje, no obstante más consciente.
• Tipo V: distinción y desambiguación. Se trata de otro tipo de aprendizaje que acompaña al alumno por un tiempo largo, iniciando muy temprano. Está presente, por ejemplo, en el campo numérico cuando se reconoce la diferencia entre un conjunto de 3 o de 5 canicas, más por percepción (el modo en el que las canicas están agrupadas, o la forma que toman los dos conjuntos) que por conteo explícito y, aunque aparentemente trivial, la distinción entre los signos gráficos que indican las letras (puede ser sorprendente, pero tal distinción se empieza a desarrollar en niños a partir de los 3 años y generalmente es mucho más sólida en niños de 5 años). En edades más avanzadas, las distinciones notables relacionadas con hechos formales son aquellas gráficas: la posición de los signos de las fracciones y de los exponentes con respecto a la base, la distinción entre los niveles de los paréntesis (redondos, angulares, corchetes), etc. Puede parecer superficial, pero en la base del aprendizaje de nuevos signos matemáticos y sus funciones específicas siempre hay una distinción: pasarla por alto, por considerarla obvia, puede ser (es) un grave error didáctico.
• Tipo VI: conceptos. Hay conceptos en la base de las adquisiciones matemáticas que son tan familiares y simples que pueden ser considerados obvios: similar, igual, diferente, agregar, quitar, etc. Si se piensa un poco, se descubre que tales conceptos se encuentran en los fundamentos de las operaciones aritméticas, de la descripción y el reconocimiento de las formas geométricas, etc., en fin, de los elementos sobre los cuales se cimienta el entero edificio matemático. Descubrir los conceptos básicos y verificar explícitamente su asimilación (teniendo como objetivo su aprendizaje) es una actividad didáctica de obligatorio cumplimiento. En el pasado, el concepto de conjuntos (y sus sinónimos) fue ampliamente impulsado y, junto con éste, el concepto de elemento. Hoy en día, cuando el entusiasmo excesivo por los conjuntos ha pasado, es aún fundamental, a mi modo de ver, la distinción entre términos colectivos y términos singulares (los cuadrados, aquel cuadrado; los números, el tres). También es obvio que la experiencia juega un papel fundamental en la adquisición de conceptos.
• Tipo VII: reglas. Se trata de un aprendizaje matemático primordial tan evidente que necesita poca explicación. Parece ser casi una peculiaridad de la Matemática, si se pone atención a lo que se dijo anteriormente sobre el término “regla”. Varios autores han contribuido al estudio psicológico del aprendizaje de reglas, entre los que recuerdo a Resnick (1967).
• Tipo VIII: problem solving. Aquí, no hay necesidad de decir otra cosa: todo el libro está dedicado a este tema. Al cual llegaremos paso a paso.
Nota bibliográfica
Para la redacción de esta sección se usaron (Gagné, 1965 [en la edición italiana, ver las pp. 55-96 y 281-324; ejemplos matemáticos (algunos por demás discutibles), pp. 292-302]; Resnick, 1967; AA. VV., 1983 [en particular los capítulos de P. Boscolo, de M. S. Veggetti y de C. Pontecorvo]; Aglì, Martini, 1995; De Zwart, 1983; Hughes, 1982; Pontecorvo, 1983, 1985; Pontecorvo, Pontecorvo, 1985; Sastre, Moreno, 1976).
Se puede encontrar una amplia panorámica de los diferentes modelos de aprendizaje, integrados a los respectivos esquemas de enseñanza que de ellos resultan, en (Ballanti, 1968). La autora dedica las cinco partes del libro al «Desarrollo», la «Adaptación evolutiva», la «Mente», el «Comportamiento y condicionamiento» y finalmente a los «Procesos y secuencias». A mi modo de ver, se trata de un proyecto sistemático de interpretación y lectura que cualquier estudioso de cuestiones didácticas debe conocer.
Asumiré como un emblema de mi punto de vista un fragmento de una célebre obra de R. A. Hinde de 1974 con el cual inicia el libro (Ballanti, 1968): «Es por demás inútil decir que el desarrollo de todas las características que conforman el comportamiento depende tanto de la naturaleza como del ambiente. Ningún carácter depende solamente de los genes o del ambiente».
Parecería de gran importancia disponer de una metodología objetiva capaz de evaluar la eficacia del trabajo desarrollado en la escuela o, en términos más generales, del esquema de enseñanza adoptado; ver (Mariani, 1991).
No se deben olvidar los aportes a los estudios sobre el aprendizaje adelantados por la ciencia cognitiva; para tal propósito, se puede leer la sección 5.4. de (Bara, 1990). Allí, se habla de aprendizaje de primer orden relacionado con el conocimiento tácito donde se sitúa la idea de aprender a aprender; ver también (Bateson, 1976); en esto se encuentra sobre todo la descripción de programas que estimulan el aprendizaje y su evolución histórica. Tendré la ocasión de volver en detalle sobre este tema en más de una oportunidad.
Con una posición muy diferente a la de Gagné, sobre la creación de los conceptos se sitúa (Aebli, 1961, pp. 228-255).
Ver también (Boscolo, 1986b), útil en términos generales y en los términos específicos aquí tratados en las pp. 8-10 (Gagné), 11-12 (Bruner), 13-22 (perspectiva cognitivista): una panorámica breve pero eficaz.
1.6. Aprendizaje operativo
Como dice un proverbio chino asumido como lema del Proyecto Nuffield en los años 70-80, es obvio que “si hago, aprendo”. Pero ese “hacer” puede ser concreto o abstracto y nadie ha dicho que el segundo (abstracto) sea menos productivo que el primero (concreto).
[Sin ir hasta la antigua China, el napolitano Giambattista Vico (1668-1744) afirmaba «verum ipsum factum» lo que esencialmente expresa la misma posición].
Dado que siempre he defendido los laboratorios de Matemática como un lugar para “hacer”, y dado que me parece una tesis evidente, evitaré entrar en detalles, por lo que me limitaré sobre este tema a las referencias bibliográficas al final de la sección.
En cambio, resaltaré un ejemplo de Vergnaud (1981a). Supongamos que hay unas barras incrustadas una sobre la otra, como se indica en la figura, y que haya que extraer la barra A.
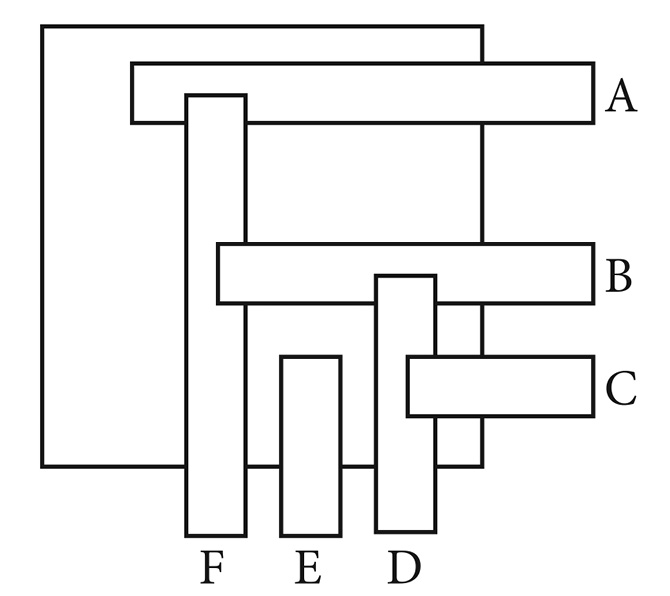
¿Qué se debe hacer?
Dado que se pide un “hacer”, es decir una acción, es evidente que hacer varios intentos es un comportamiento espontáneo. «Intento sacar la A, pero no se mueve. Bien: dado que A está bloqueada por F, sacaré la F; pero la E está libre; podría sacarla; (…)» y así sucesivamente.
Claro que es un ejercicio útil dentro de lo que se podría llamar un cálculo de las relaciones: para sacar A, primero se debe extraer F; pero (…) Me parece que no se acentúa suficientemente lo que es inútil hacer: «Si quiero sacar A, es inútil extraer E». Me parece que este dualismo: “es necesario / es inútil”, acierta la dimensión exacta y significativa del sentido que tiene el orden de las operaciones a seguir.
Solo que, si se hace el estudio en forma concreta, a mi modo de ver, se pierde mucho. Una vez hecha una acción, ésta perdura a manera de efecto en la memoria solo durante el tiempo de la acción y por lo tanto no puede influenciar la consciencia profundamente. En casos de este tipo, parece muy fructífero resolver el problema de manera puramente mental, si acaso reforzando la resolución con expresiones verbales, orales o escritas: «Si quisiera sacar A, primero debo extraer F; en realidad, no lo hago, pero supongo que lo quiero hacer; si quisiera extraer F, antes debo (...)». Entonces, hay aprendizajes operativos que no pasan a través de una operación concreta, “realizada”, sino solo imaginada. Esta modalidad refuerza el aprendizaje, favorece la imaginación y obliga a tener una expresión verbal coherente y significativa.
También en la fase de ejecución de los problemas, es esencial que exista el hábito de hacer explícitas las diferentes fases de la resolución, lo que es una forma segura de estudiar significativamente las estrategias resolutivas reales y, niño por niño, el estilo de quien resuelve. (Sin embargo, el análisis crítico de los protocolos de observación y las entrevistas son también “formas” válidas).
Favorecer la imaginación operativa hace posible resolver problemas particularmente difíciles. Tomo prestado otra vez una idea de Vergnaud (1981): «Miguel tiene una vasija con dulces. Inés toma 15 para ella. José le da a Miguel otros 9 dulces. Ahora, Miguel tiene en total 63 dulces ¿Cuántos tenía al principio?».
Niños de tercero de primaria que no tienen el entrenamiento para imaginar la solución, en un porcentaje muy alto, no saben resolver el problema. Niños de la misma edad, entrenados para “ver la situación”, imaginan operativamente las diferentes escenas y hacen las cuentas a la inversa (aunque no formalizándolas): «Cuando José da los nuevos dulces a Miguel, Miguel tiene 63-9 o sea 54. Cuando Inés toma 15 dulces, Miguel tenía 54+15 o sea 69». Operativamente, paso a paso, imaginando las escenas, el porcentaje de solución aumenta notablemente.
Se puede tratar de ayudar a los niños dándoles un esquema gráfico como el siguiente:
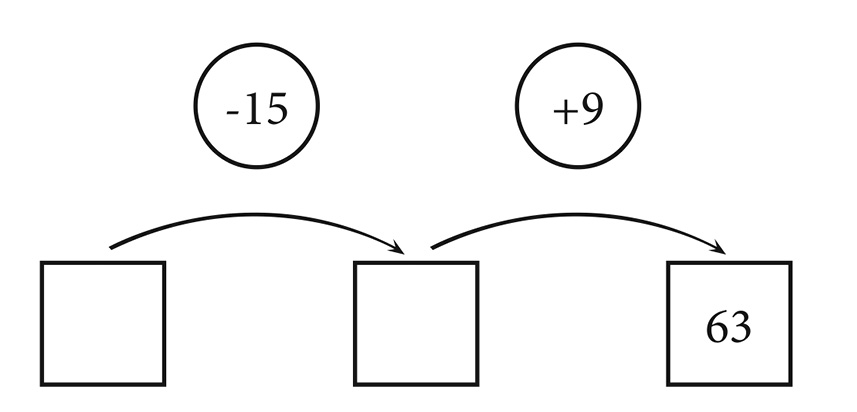
¿Cuánto puede ayudar este esquema a la solución dada por los niños? Ayuda mucho en el caso de niños no entrenados a imaginar (el porcentaje de soluciones aceptables pasa, en nuestros experimentos, de casi cero al 60%); ayuda poco en el caso de niños entrenados para imaginar, en el sentido en el que estos niños ya eran buenos en la actividad de resolver este tipo de problemas y por lo tanto el esquema tiene sí una incidencia, pero ésta no es sustancial. De tal manera que el esquema ayuda sobre todo a quien no sabe ayudarse solo.
[También hemos intentado hacer el proceso inverso: dar el problema con el esquema sugerido; entonces, el porcentaje de respuestas correctas (siempre de niños de tercero) es inmediatamente más elevado. Al dar un problema análogo, sin esquema, muchos niños reutilizan uno parecido al entregado anteriormente (en este caso se ve una discreta transferencia de aprendizajes) resolviendo así el problema en un buen porcentaje. Solo que (…) Intentamos dar un tercer problema, para el cual el esquema anterior no tenía ningún sentido. Entonces, constatamos que los niños que siguen un programa de enseñanza usual, aún antes de analizar la solicitud del texto, dibujaban el esquema, adoptando una especie de regla: «Si el esquema gráfico funcionó dos veces, ¡funcionará siempre!». Detrás de este comportamiento está la idea del contrato didáctico en cuanto “el niño tiene la expectativa de modalidades repetitivas”].
Tendremos que volver largamente sobre estos temas, de manera más profunda y desde diferentes puntos de vista.
Sin embargo, antes de proceder, me gustaría resaltar que el problema de Miguel y los dulces parece involucrar con fuerza el concepto de incógnita; quien resuelve se debe hacer una imagen mental fuerte de esta idea: ¿qué debo encontrar exactamente? Y aquí hay dos incógnitas, una que resuelve el problema final y una intermedia, por decirlo así.
Es importante evaluar también este aspecto en el estudio específico de este problema (u otros análogos).
Nota bibliográfica
Para la redacción de esta sección, utilicé (Vergnaud, 1981a; D’Amore, 1988c; D’Amore, 1990-91; Caldelli, D’Amore, 1986).
Otros textos básicos (D’Amore, Marazzani, 2011; D’Amore, Persano, 1985; D’Amore, Sandri, 1991).
Para un fundamento pedagógico sobre el uso de los laboratorios, ver (De Bartolomeis, 1979)
1.7. Jerarquías de aprendizaje y problemas de “inmersión total”
En la sección 1.5. vimos como varios autores, en particular Gagné, proporcionan, por así decirlo, una jerarquía de los aprendizajes, distinguiéndolos desde los más simples (aquellos que se hallan también en los animales) hasta los más complejos. Si aprender a resolver problemas significa en gran medida utilizar conceptos aprendidos, entonces también la escala propuesta por L. E. Bourne (1966) nos puede proporcionar una reflexión útil sobre el tema; Bourne propone 4 tipos fundamentales de tareas conceptuales:
• aprendizaje de atributos: dando un estímulo y proponiendo posibles atributos, el sujeto distingue entre éstos; es un tipo de aprendizaje que está relacionado con la percepción (la individuación de las características típicas de un objeto, aquellas que lo hacen diferente de los demás) y la etiqueta (labeling) (se asocia un sustantivo a un objeto-estímulo);
• uso de los atributos: es la fase sucesiva; hay atributos que el sujeto ha individuado y que, por lo tanto, se encuentran a su disposición; ahora el sujeto escoge aquellos atributos que hacen que el objeto sea parte de un conjunto o categoría (esto sustancialmente es la “tarea de identificación del concepto de un determinado tipo” de Bruner, 1960);
• aprendizaje de reglas: mediante la experiencia, el sujeto aprende reglas comunes para ciertas clases de situaciones;
• uso de las reglas: a su vez, las reglas son un instrumento para adquirir un comportamiento conceptual; éste es el clásico caso de la resolución de problemas. Aún dentro de sus límites (señalados por Boscolo, 1986, pero también por el mismo Bourne), esta clasificación es útil aquí solo para ampliar el panorama de los estudios sobre el tema de las jerarquías del aprendizaje que han fascinado a los psicólogos.
Algunos de ellos han afrontado temas muy particulares; por ejemplo, Gagné, Mayor, Garstens y Paradise publicaron en 1962 una investigación sobre las jerarquías relacionada con la adición de los números naturales (ver Resnick y Ford, 1991, pp. 39-41); Gagné y Briggs (1974) estudiaron la sustracción de números naturales (ídem); etc.
Si bien muchos lectores críticos tienden a despreciar estos análisis (creo que lo hacen sobre todo los lectores matemáticos), es necesario reconocer que tienen al menos una función: hacer reflexionar sobre la complejidad de algo que, desde cierto punto en adelante, se podría pensar que posee el mismo nivel de dificultad, tanto como para sugerir que no hay diferencia entre los casos. En definitiva: ¿es la sustracción en sí la que presenta dificultades conceptuales o son los casos individuales, o son las modalidades en las cuales se presenta que plantean dificultades de diferente tipo? Parecería que la segunda posición no es del todo trivial. Las habilidades estudiadas son habilidades de desempeño es decir lo que el sujeto sabe hacer en casos particulares (dado que no se hacen preguntas abstractas o generales sobre la sustracción, por ejemplo, en sí, pero se proponen situaciones). Sin embargo, Gagné en particular, pero también otros autores, llegan incluso a sacar conclusiones sobre las habilidades intelectuales, las cuales nos interesan más. Además: la naturaleza de las jerarquías de aprendizaje es tal que se pueden distinguir tareas subordinadas a otras y que son componentes de actividades de orden superior; se tendría por lo tanto una especie de aprendizaje no solo en forma de espiral sino también en forma de escalera, en la cual cada peldaño es necesario para poder dar el paso sucesivo. Sobre este tema (denominémoslo “teoría de los prerrequisitos”) ha trabajado por ejemplo Flavell (1972); las capacidades iniciales se transforman en elementos fundamentales para capacidades sucesivas; algunos desempeños y comportamientos fundamentales en el pasado pueden desaparecer del comportamiento de un niño que, después de algún tiempo, ya no tiene necesidad de dar los mismos pasos. Flavell concibe esta jerarquía como una forma de conceptualizar la Matemática misma (más allá de su aprendizaje). También es cierto el hecho que, si una tarea ocupe una posición elevada en una jerarquía de aprendizaje, no significa que sea más difícil de aprender o que requiera más tiempo que tareas anteriores; sin embargo, su posición en la jerarquía de todas maneras indica la “riqueza” de sus componentes. Al contrario, puede muy bien suceder que las tareas de nivel inferior sean las más difíciles de realizar por motivos de edad, falta de hábito u otros. En un estudio de Carroll de 1973, se muestran ejemplos concretos de todo esto: si una tarea considerada muy difícil se descompone en todos sus elementos elementales y el sujeto posee estos elementos, el último “peldaño” se vuelve sencillo y el niño puede realizar la tarea solo y en tiempos breves. Es más, le quedaría fácil transferirlo de una red compleja de peldaños inferiores hasta llegar al último peldaño. Hay que decir que con frecuencia los peldaños inferiores de una jerarquía son los fundamentos de muchos otros aprendizajes y por lo tanto se prestan a transferencias sucesivas incluso en otros ambientes conceptuales: saltarlos para proponer inmediatamente actividades complejas podría ser un error, ya que se eliminarían las bases para otras escalas del aprendizaje. La palabra clave que emerge de estos estudios se puede resumir así: ir de lo simple a lo complejo, en la práctica didáctica.
Sin embargo ¿quién nos puede asegurar que todo esto sea correcto, que tenga sentido, que sea aceptable y funcional?
Muchos psicólogos han dedicado amplios estudios a verificar la validez de estas jerarquías de aprendizaje. Según la técnica usada, podemos distinguir estos estudios en dos categorías: estudios escalares (scaling study) y estudios de adestramiento (training study).
En un scaling study se somete a un grupo de estudiantes a test relativos a los prerrequisitos de una tarea que debe ser objeto de estudio; cada alumno recibe un puntaje + o – en cada “peldaño” (habilidades componentes). Entonces, los estudiantes se organizan del “mejor” (el que tuvo más +) al “peor” (el que obtuvo más –). De tal manera que se provee una tarea de orden jerárquico más elevado y se verifica la evolución del grupo de alumnos. Si la jerarquía de aprendizaje (en esa posición particular) es correcta, tendremos que poseer una escala de respuestas correctas que corresponda al orden de los estudiantes; es decir, el “mejor” es también aquel que resolverá el test de la mejor manera, el “peor” viceversa. Si esto no sucede, entonces la escala de aprendizaje no es la correcta. Guttman en los años 40 (1944) diseñó esta prueba, por lo que la disposición de los + y los – obtenidos por el grupo de estudiantes es llamada escala de Guttman. Otros estudios sobre esta cuestión fueron propuestos por muchos autores, cito el estudio de Wang, Resnick y Boozer (1971) porque se dedica a las diversas tareas básicas en Matemática. De este estudio resultó que no hay dependencia entre la capacidad que tienen los niños pequeños para contar y el saber proponer una correspondencia uno a uno entre los elementos de dos conjuntos; y no solo esto, sino que su posición en una jerarquía es totalmente intercambiable. Este resultado tuvo una gran incidencia sobre cierta legión de defensores a ultranza de lo que se ha denominado Matemática moderna (dada la delicadeza de la cuestión y la “polvareda” que levantó, Wang llevó a cabo otros estudios en 1973, también Gelman y Gallistel en 1978, entre otros, y todos encontraron el mismo resultado). El scaling study ha sido últimamente sometido a varias críticas, algunas obvias, que pasaré por alto (se pueden encontrar en Resnick y Ford, 1991, pp. 45-47).

